基于交叉克尔对称模和反对称模的光子反聚束

祝卿皓， 刘洪雨

( 延边大学 理学院，吉林 延吉 133002 )

单光子源是在单光子水平进行量子信息处理的基本设备之一.1997年，Imamoglu等首次用四能级原子制备了单光子源，且发现该单光子源具有很强的光子反聚束效应(光子阻塞效应)[1].随后，一些学者在不同的系统中也发现了强光子反聚束效应，如囚禁原子的光学腔[2]、光子晶体中的量子点[3]和电路量子电动力学系统[4].2010年，Liew等在由两个线性耦合的非线性腔模组成的光子分子中发现，当非线性远小于腔模的衰减率时，该系统也可以产生强光子反聚束[5].基于这一发现，学者们提出了许多不同的系统来实现光子阻塞，如具有量子点的双模光学腔[6]、具有二阶或三阶非线性的耦合腔[7-9]以及耦合光机系统[10]、非线性光子分子[11]、交叉克尔非线性[12]等.基于上述研究，本文将研究由两个线性耦合的非线性腔组成的光学模(对称模和反对称模)的光子反聚束效应，并证明了该对称模和反对称模的非线性无论强弱都可以产生较强的反聚束效应.另外，本文还分析了在双模驱动作用和存在双模驱动相位时光子反聚束效应的变化情况.

1 理论模型

本文考虑由两个单模光场组成的模型.在该模型中，两个光学模通过相互作用和交叉克尔相互作用耦合在一起.系统的哈密顿量为(ħ=1)：

H=Δaa†a+Δbb†b+J(a†b+b†a)+Ga†ab†b+E(a†+a)+F(b†ei δ+be-i δ).

(1)

(2)

系统的动力学方程为：

(3)

其中κa(κb)是模A(B)的耗散率.由于本文的分析均是在热平衡下进行，故忽略了平均热光子数对系统的影响，同时假设模A和模B的耗散率相等，即κa=κb=κ.

为了研究对称模和反对称模的光子统计性质，本文给出如下归一化的二阶关联函数[13]：

(4)

稳态情况下，式中的τ是不同探测器之间的时间延时.通过数值求解方程(3)(主方程)可得到截断Fock态空间的密度矩阵，进而可得到对称模和反对称模的二阶关联函数.

2 光子阻塞的优化条件

在弱驱动条件(E≪κ)下，对称模和反对称模的Fock态基可由|m,n〉表示，其中m表示对称模的光子数，n表示反对称模的光子数.为了研究对称模和反对称模的光子阻塞效应，可将系统的波函数用Fock态基(|0,0〉，|1,0〉，|0,1〉，|2,0〉，|1,1〉，|0,2〉)展开：

|ψ〉=C00|0,0〉+C10|1,0〉+C01|0,1〉+C20|2,0〉+C11|1,1〉+C02|0,2〉,

(5)

其中|n+,n-〉表示对称模n+光子和反对称模n-光子的Fock态.将方程(5)和方程(2)代入薛定谔方程可得到系数为Cn+n-的动力学方程：

(6)

由弱驱动条件可知|C00|≫{|C10|,|C01|}≫{|C20|,|C11|,|C02|}，进而知方程(6)的单光子态系数方程可描述为：

(7)

(8)

双光子态的系数方程为：

(9)

(10)

(11)

为了简便起见，假设F=nE，则从方程(7)和方程(8)可得到系数C10和C01的关系为：

(12)

将方程(12)代入方程(9)和方程(10)可得：

(13)

(14)

通过求解上述2个方程可得

(15)

式中的实部和虚部都为0.为简便起见，假设n=0，则系统模型可转化为单模驱动情形，并可得到阻塞的最优条件：G=4(J-Δ),4J2-4Δ2-κ2=0.

3 数值模拟

图1 零延时二阶关联函数和随交叉克尔相互作用强度G/κ和失谐Δ/κ变化的对数图

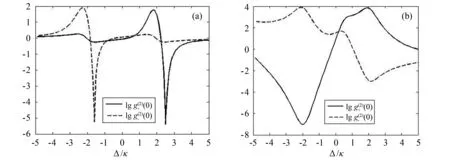
图2 零延时二阶关联函数(实线)和(虚线)随失谐Δ/κ变化的对数图

图4 零延时二阶关联函数随驱动强度比例系数n变化的对数图

图5 零延时二阶关联函数随两个驱动场之间的相位差变化的对数图

4 结论

本文对由两个线性耦合的非线性腔模组成的对称模和反对称模的光子阻塞效应进行研究表明，对称模和反对称模的非线性无论强弱都可以产生较强的反聚束效应.在最佳条件下对光子阻塞效应进行分析表明，当系统中存在双驱动和驱动相位差时，系统均可获得强光子反聚束.综上表明，本文的系统可以通过调节非线性腔模之间的耦合强度来控制光子的反聚束效应.本文研究结果对在实验中实现可调谐单光子源具有良好的参考价值.