“画数学”：让数学丰满起来

黄荣

【摘要】“画数学”是学生在学习数学的过程中，用画图的方式将复杂的数量关系用图形的方式呈现出来，或用画图的方式将自己的思考过程梳理出来，这些图可以是集合图、實物图、线段图、示意图、树形图等各种形象直观的图形，概括来讲就是结合“数形结合”的数学思想来学习数学。

【关键词】数学;认识负数;案例分析

一、整理信息，初步感知

师：今天这节课，我们一起来研究负数。你们听说过负数吗？在哪见过？

生1：我在电梯里看到电梯上有-1层、-2层。（师板书：-2）

生2：冬天的时候很冷，气温零下几度。（师板书：-5℃）

生3：我看到妈妈银行本上取钱显示负多少。

师补充：盆地的海拔用负数表示。（师板书：-155米）

师：通过举例，我们对负数有了初步的感觉，今天我们要让感觉变成一种认识。

二、画出数学，探究新知

师：你会用简单的示意图表示对3个负数的理解吗？四人一组完成交流，依次说明怎么表示的，其他人想的一样吗？有什么补充？

探究要求：

（1）想一想：信息所表达的含义。

（2）画一画：用简单的示意图表示对信息的理解。

（3）说一说：在小组内说一说你的想法。

（师：不会说的同学可以听听其他同学的想法，倾听也是一种学习。）

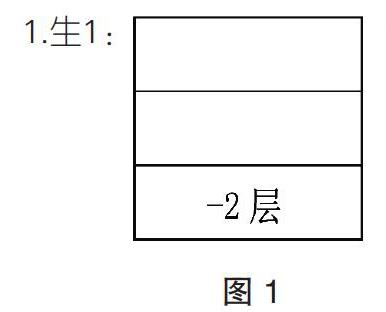
（一）展示学生图形：芳芳家的车停在-2层

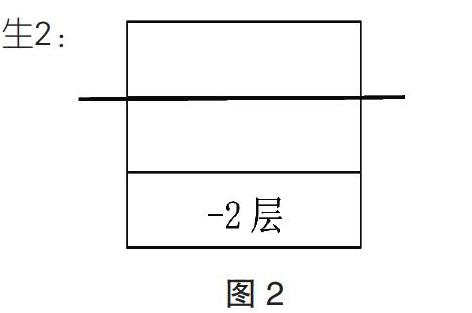
1.生1：   生2：

2.师提问：第二个同学的图比第一个同学的图有什么更特别的地方？

生：第二个同学把地面做了特别强调，以地面作为参照物，把地面与地下分隔开。

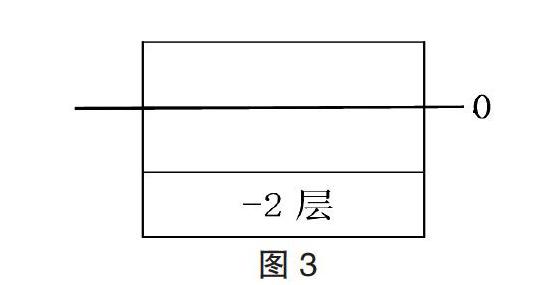
3.师：补充图形：在这里我们把地面用0来标注。

4.师：看大屏幕，请同学们来看看老师画的这个楼层，猜猜看？号表示的是几层呢？

生1：可能是-1层。

生2：我觉得可能是-2层。

师提问：为什么楼层没动而同学们给出的结论各不相同呢？

生：地面没有确定，楼层会随着地面的改变而改变。

师：（给出地面位置图5）老师规定这是地面，你能确定这是第几层吗？

生：-1层。

师：（移动地面图6）现在呢？

生：-2层。

师：现在你知道什么叫-2层了吗？

（二）展示学生图形：今日最低温度是-5℃

生1：一幅下雪图，同时标注下雪，-5℃。

生2：一个标注好-5℃的温度计。

生3补充：生1只是对-5℃的感觉，生2既有对-5℃的感觉，又有对-5℃的认识。

师提问：温度计上为什么一定要画0℃，只画一个-5℃不行吗？

生：没有0℃就没有比较了。

（三）展示学生图形：吐鲁番盆地的海拔高度是-155米

生1：  生2：

师：通过0来判断正负。

（四）引申出数轴

师：我们刚已经认识了正数、负数和0，其实在数学中我们还可以用数轴来表示数，（画数轴）以0为界，正数在0的右边，负数在0的左边，那0在哪呢？0既不是正数，也不是负数，0在中间，正数比0大（补充0<正数），负数比0小（补充负数<0），这就是我们今后会学习研究的数轴。

三、整理归纳，总结提升

今天这节课的学习，同学们有了哪些新的收获呢？负数在生活中有着广泛的应用，以后我们会继续学习。

（一）“画数学”在教学中的价值

1.“画数学”简化题意，有助于加深理解

从教育学的角度看，儿童年龄小，识记枯燥而又陌生的定义、概念、数学名称时显然很吃力，而记忆具体的时间、知识、对象、人物、事实就相对容易些，并且记得更牢固。如在教学进位加法时，教师可以让学生自主画出小棒图来理解计算过程，这样的做法有助于帮助学生把抽象算理转化为具体图画的形象记忆。

2.“画数学”分析数量关系，有助于解决问题

教师经常鼓励学生在解决一些实际问题的时候用图的形式画出来，把抽象的文字描述变成直观的图形，做到边理解题意边观察图形，那么学生对数量关系的理解就会变得更加清晰，学生快速找到解决问题的方法。

3.“画数学”没有限制，有助于开拓思维

“画数学”是让学生用“画”的方式呈现出自己对于数学问题的理解，这一过程学生可以自主利用自己所能想到的所有工具，材料不限，形式不限，自由思考，不断创造，从而找到独特的解决问题的方法，提出富有创造性思维的设想。

（二）“画数学”在小学数学教学中的运用

1.在数的概念中渗透数形结合

数的概念是形成数学知识体系的基础。但对于以形象思维为主的小学生来说，数的概念不是具体的而是抽象的，这需要学生用画的方法把抽象的概念转化成具体的图形，从图中理解数的概念，梳理各种概念之间的关系。本节课就巧妙地借助“画数学”的方式帮助学生理解负数的含义。负数原本是抽象的概念，学生一般只能通过枯燥的文字记忆，但经过图形的转换，枯燥的文字也能变成生动的图形来记忆，不仅便于学生理解，而且能加深记忆，教师的教学过程也显得具体形象化。

2.在系统复习中“画数学”渗透数形结合

“画数学”在复习课中可以通过表格、思维导图、树状图等的方式呈现。复习课就是将看似零散的数学知识加以梳理，将它们重新呈现。毫无章法的简单文字呈现并不能对学生的复习带来帮助，简洁明了的图像能将这一过程去繁从简，帮助学生将零散的知识点梳理成一个完整的知识体系。

以全国著名特级教师贲友林所教的六年级“平面图像的面积总复习”为例。课前，学生自主完成了学习单，第1问：“我们已经学过哪些平面图像的面积计算？你能用表格或画图的方式将所学的平面图形面积计算的知识进行整理吗？”课上，教师直接展示了学生的的汇总信息。学生各自讲解自己梳理的过程、各个知识之间存在的联系。有的学生采用文字罗列的方式，显得比较累赘，不够简洁明了;有的学生采用图像加字母加思维导图的方式，显得清晰明了，并能看出知识点之间的联系;有的学生采用画树形生长图的方式，既新颖又清晰。用画图的方法把枯燥的公式转化成规则的图形，学生感受到数形结合的直观性和便捷性。绘制图形这一过程是学生自我梳理知识点的过程，对图形再次进行讲解的过程也是再一次加深印象，教师能顺着学生的思路进行及时补充和讲解。

（三）“画数学”在小学数学运用中的建议

“画数学”是教与学的一种重要方法，更是一种数形结合思想，通过“以数解形”或者“以形助数”，把抽象难懂的数学语言、数量关系与直观形象的几何图形相结合，使复杂的问题简单形象化，从而为解决问题开辟一条新的道路。“画数学”是用数形结合思想解决问题的一种方法，但绝对不是唯一的方法。在解决问题的过程中，应该具体问题具体分析，找到适合每一题的具体方法。在用数形结合的方法解决问题的过程中，更重要的是要在潜移默化中向学生渗透这一思想，为学生今后解决问题提供更多的选择。

【参考文献】

李付英.小学数学教学中学生数学思维的培养探讨[J].东西南北，2019（08）.

马俊清.小学数学教学中培养学生数学思维的策略研究[J].读写算，2019（31）.