基于动态有序矩阵的外辐射源雷达CFAR算法

饶云华 周健康 万显荣② 龚子平② 柯亨玉②

①(武汉大学电子信息学院 武汉 430072)

②(武汉大学深圳研究院 深圳 518063)

1 引言

在外辐射源雷达低空小目标探测中，其背景杂波受传播环境影响而复杂多变，尤其是功率突变的杂波会在距离多普勒谱上形成点状、块状的杂波边缘，极大地影响了低空小目标的恒虚警检测性能。

当前常用的恒虚警算法根据杂波在空间与时序上的分布特性与均匀性可划分为：空域类(也称为滑窗类)和时序类。

空域类恒虚警算法中具有代表性的是单元平均(Cell Averaging)CA-CFAR算法[1,2]，其采用临近待检测单元的杂波均值来计算检测阈值，在均匀环境下效果较好，但是在多目标及杂波边缘环境下无法消除临近目标与能量突变干扰，使得检测性能恶化。在该算法的基础上，Trunk[3]提出了最小选择(Smallest Of)SO-CFAR以解决多目标干扰问题，Hansen等人[4]提出最大选择(Greatest Of)GO-CFAR以解决杂波边缘环境下的能量突变问题，但是这两种算法都在均匀环境下存在一定性能损失，且并不适用于另一种非均匀环境。Smith等人[5]在以上算法的基础上提出了变指数(Varibility Index)VI-CFAR。该算法先判决当前杂波环境的类型，然后选择与其匹配的其他恒虚警算法[6,7]，其本质是多种算法的组合。Rohling等人[8-11]提出有序统计(Order Statistics)OS-CFAR，虽然该算法在多目标、杂波边缘环境下性能得到部分改善，但在均匀环境下性能也有一定损失。

时序类恒虚警算法[12-16]中，杂波图(Clutter Map)CM-CFAR是该类算法的典型代表，CM-CFAR将杂波空间划分为杂波图单元用以存储杂波数据，每个杂波图单元依靠当前数据和历史数据进行加权迭代更新。由于这类算法在迭代初期采样的数据量少，所以检测性能较差；随着迭代次数增加，检测性能会得到较大的提升。但是这类算法也具有因迭代计算而带来的记忆效应这一不可忽视的缺点。

在外辐射源雷达低空小目标探测中，由于目标回波弱、背景杂波复杂多变，空域类算法在该类应用中性能损失严重、虚警概率恶化，传统时序类算法迭代初期性能较差并且还有记忆效应等问题，为此本文提出了动态有序矩阵(Dynamic Order Matrix)DOM-CFAR算法，其将杂波空间划分成有序矩阵，利用雷达初次扫描数据的滑窗中值对有序矩阵中的有序数组进行初始化用以弥补传统时序类算法在迭代初期的性能劣势，并通过雷达扫描数据对有序数组进行动态极值替换用以获取杂波估计中值并弥补记忆效应造成的影响，最后利用杂波估计中值来 计算检测阈值。

2 检测模型

2.1 杂波与目标

在判决雷达回波x (t)中是否存在目标时，根据二元假设检测可知

其中， s(t) 为目标信号，n (t)为杂波和噪声信号，H0表示只有杂波，H1表示存在目标。

杂波分布模型按照其概率密度函数参数个数可以分为单参和多参分布模型[17-20]。例如瑞利分布、指数分布等只由1个参数决定其幅度分布规律的为单参分布模型；韦布尔分布、对数正态分布、莱斯分布等由多个参数决定其幅度分布规律的为多参分布模型。本文以杂波数据经平方率检波后服从指数分布为背景，其杂波概率密度函数(Probability Density Function, PDF)为

其中， λ为每个杂波单元总功率。在H0假设下，λ为杂波和噪声的功率µ ；在H1假 设下，λ 为杂波、噪声和目标的总功率 ( 1+s)µ , s表示目标与杂波噪声功率 µ的比值。由式(2)可得检测概率(Probabi lity of Detection, PD)与虚警概率(Probability of False Alarm, PFA)为

在已知参数µ 和预设虚警概率P FA时，可由式(4)求得检测阈值T为

2.2 有序矩阵

对于雷达回波的RD谱数据 X，每帧数据既有距离信息也有多普勒信息，其表达式为

其中， xr,d表示RD谱 X 中待检测的第( r,d)单元数据，其中r 为第r 个距离元、d 为第d 个多普勒元。由于本文所提算法利用待检测杂波的历史数据来估计中值 ymid求解检测阈值T，为了准确地估算估计中值 ymid，这里利用有序矩阵 M来存储相关历史数据，有序矩阵 M的表达式为

其中， Yr,d为有序矩阵 M 中第( r,d)单元的有序数组，其长度为 2 K+1， 用于存储xr,d历史数据，表达式为

其中， yk为 有序数组Yr,d中 的第k 大的数据， K 为本算法的半参考窗值，K值越大，所需的存储空间越多。待检测单元xr,d的 杂波估计中值ymid为Yr,d中的yK+1。

3 DOM-CFAR原理

DOM-CFAR算法实现流程如图1所示，分为初始化、迭代优化与检测3个步骤。

3.1 初始化

初始化后，有序数组 Yr,d中的数据yk服从N(u0+τ,σ2)的高斯分布，其均值与方差为

其中， u0为杂波理论中值，τ 为yk与u0的差值，σ2表示yk的方差。

由式(9)可知，初始化后有序数组Yr,d中 yk的 数值都为，方差值为0，并且当K值越大，采样滑窗所包含的杂波样本越多，越趋近u0，| τ|数值越小。

由于本算法初始化参考OS-CFAR的采样策略 ，所以在迭代初期可获得与其接近的算法性能。

3.2 迭代优化

算法迭代通过将有序数组Yr,d中偏离理论中值u0的 数据替换，保留接近u0的数据，从而获取更加准确的估计中值ymid。

图1 DOM-CFAR算法实现流程图

在数值替换中对极小值 y1和极大值y2K+1进行动态轮询替换，以雷达扫描次数t的奇偶性为标志，当雷达扫描次数t为奇数时，将待检测单元xr,d赋值给 Yr,d中 的y1；当t为偶数时，将xr,d赋值给y2K+1。重新对Yr,d进行排序以保持有序性，以被替换极值点为起点，未被替换极值点为终点进行单向冒泡排序。K值越大，排序耗时越多。

由于初始化时Yr,d中的数据都相同，所以在算法迭代中需要经过2K+1轮迭代才能将 Yr,d中的初始数据全部替换，之后 Yr,d中的ymid开始变化，初始数据被全部替换也标志着算法渡过2K+1轮迭代的 初期阶段。

3.3 检测阈值计算

使用本算法进行检测处理时，若杂波数据服从单参分布模型，可直接按原流程处理；若杂波数据服从多参分布模型，则需要先保留其中1个参数为未知状态，将其它参数由参数估计方法(最大似然估计、矩估计等)估算，之后按照原流程估算这个未 知参数，计算检测阈值进行检测处理。

3.4 半参考窗值K的取值

半参考窗数值K需要综合考虑内存需求、运算速度、迭代速度、期望检测性能这4个因素进行设置。为便于分析K值对迭代速度和期望检测性能的影响，这里设计如下2个评价指标

其中， yt,K,i为 杂波估计中值，为杂波理论中值， mt,K为yt,K,i与之差绝对值的均值，为yt,K,i与之差绝对值的方差，t 为迭代次数， K为半参考窗值， i为蒙特卡罗实验次数， N为蒙特卡罗实验总次数。均值 mt,K越小，表明yt,K,i越接近、准确性越高；方差越小，表明稳定性越高；准确性与稳定性越高计算出的检测阈值更接近理论值，可获得更优的期望检测性能。

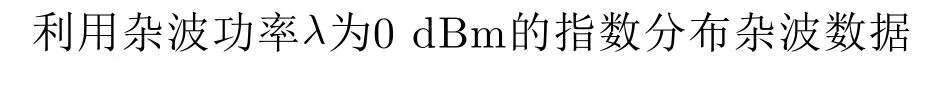
由图2、图3可知，两图左上角出现三角形异常区域，这是由算法迭代初期杂波估计中值不变暂稳态导致。K取值在[10,20]范围内时，两图的评价指标处于等高线山谷区域，均值和方差较低(异常区域数据除外)，准确性和稳定性较高，所以应尽量将 K取值在[10,20]范围内。

4 仿真分析

将DOM-CFAR与最优检测器(opt), CA-CFAR,SO-CFAR, GO-CFAR, OS-CFAR和CM-CFAR进行4×103组蒙特卡罗仿真实验，其中背景杂波功率λ为20 dBm, DOM-CFAR的半参考窗值K为15,CA-CFAR, SO-CFAR, GO-CFAR和OS-CFAR的保护单元为4、滑窗长度为30, CM-CFAR的遗忘因子 为1/128，预设虚警概率PFA为10-4。

4.1 均匀环境下的性能分析

对均匀环境下单目标分别进行10次、200次、1000次迭代优化，其中信杂比取值范围为[0 dB,30 dB]，其检测结果如图4、图5、图6所示。

由图4可知，DOM迭代初期检测性能接近OS，优于SO，较CA, GO略差。

由图5可知，经过200次迭代DOM性能已优于参照对比算法。

图2 均值等高线

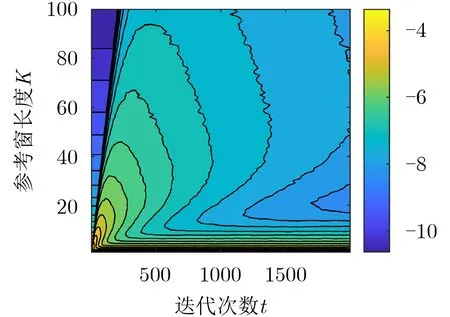
图3 方差等高线

由图6可知，经过1000次迭代DOM性能趋近于最 优检测器性能。

4.2 多目标环境下的性能分析

在目标参考前窗设置相同信杂比的第2个目标形成拥有多目标的背景杂波环境进行10次、200次迭代优化，其中信杂比取值范围为[0 dB, 30 dB]，检测结果如图7、图8所示。

由图7可知，DOM迭代初期拥有与OS相近的多目标检测优势。

由图8可知，DOM检测性能不受邻近目标的影响，且经过200次迭代后，其检测性能已经优于参照 对比算法。

4.3 杂波边缘环境下的性能分析

设置前500个距离单元杂波功率为20 dBm，后500个距离单元杂波功率为30 dBm，形成杂波边缘环境，分别进行10次、200次迭代检测，其结果如图9、图10。

由图9可知，DOM迭代初期的虚警概率在杂波边缘的低功率区相较于CA, GO和CM更接近预设值，在杂波边缘的高功率区相较于CA, SO更接近预设值。

图4 均匀杂波下迭代10次

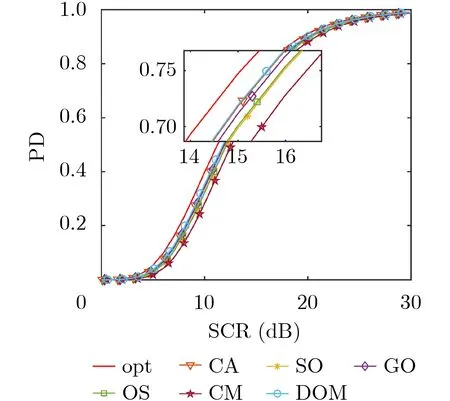
图5 均匀杂波下迭代200次

图6 均匀杂波下迭代1000次

图7 多目标下迭代10次

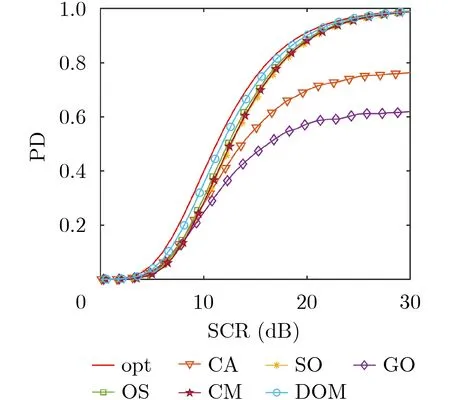
图8 多目标下迭代200次

图9 杂波边缘下迭代10次

由图10可知，DOM经过200次迭代，虚警概率在杂波边缘的低功率区更接近预设值，在杂波边缘的 高功率区相较于CA, SO和OS更接近预设值。

4.4 记忆效应分析

DOM与CM都是利用杂波历史数据计算检测阈值的时序类恒虚警算法，算法处理时每帧数据(无论是否有目标能量信息)都参与迭代并影响后续检测，从而导致算法的记忆效应。

由于DOM的参考数据为估计中值xDOM(t), CM的参考数据为估计均值xCM(t)，为了统一评价指标进行如下处理

其中， PdB为杂波功率值，为理论中值，为 理论均值。评价指标s 的数值越小，参考值越接近理论值，估算的检测阈值更准确。

先在均匀杂波无目标的环境下进行2000次迭代使DOM和CM的性能稳定，从第2001次迭代开始，连续引入50次单目标回波，仿真目标能量参与迭代对性能的影响，其中目标能量信杂比分别为4 dB,8 dB, 16 dB，结果如图11所示。

由图11可知，当目标干扰出现并参与迭代，对DOM的影响有一定延时，当目标干扰消失时，DOM会以更快的速度重新优化，故其拥有更优的抗目标干 扰能力。

4.5 算法复杂度与耗时

由于算法中每个待检测单元都需要一组长度为2K+1的有序数组用于存储其历史数据，因此空间复杂度(使用大O表示法)为O(MK)，其中M由待检测单元总个数决定。在迭代优化中动态极值替换的逻辑计算量很小几乎可以忽略，对运算速度起决定影响的是单向冒泡排序，因此其运算复杂度为O(K)。

图10 杂波边缘下迭代200次

以大O表示法为评价指标对各个算法的空间、运算复杂度以及在硬件为i7-7700HQ CPU条件下处理10帧实测RD谱数据的串行、并行计算耗时进行分析，结果如表1所示，其中N由滑窗大小决定、K由半参考窗值决定、M由待检测单元总个数决定。

由表1及前文中各算法在均匀、多目标和杂波边缘环境下的性能对比可知，本算法与现有大部分算法相比，虽然存储空间需求较大、处理速度优势不突出，但在性能上得到了较大提高。同时根据已进行的雷达低空小目标探测实验可知，其算法复杂度对于目前的GPU硬件条件来说是可行的。

5 实测数据验证

使用武汉大学电波传播实验室的外辐射源雷达系统[21]在有风力发电机组环境下的实测数据进行验证分析，探测条件如图12所示。

实测数据经多径杂波和多普勒扩展杂波抑制后的RD谱中，风机叶片转动的多普勒扩展杂波残余仍然较强，形成杂波边缘环境，如图13所示。

在实测RD谱上添加100个信杂比为15 dB的随机目标则形成拥有多目标的杂波边缘环境。将DOM-CFAR与CA-CFAR, SO-CFAR, GO-CFAR,OS-CFAR和CM-CFAR进行实测验证，其中DOM-CFAR的半参考窗值K为15, CA-CFAR,SO-CFAR, GO-CFAR和OS-CFAR的保护单元为4、滑窗长度为30, CM-CFAR的遗忘因子为1/128，迭代总次数为400，预设虚警概率为10-6，结果如表2所示。

图11 目标干扰对性能的影响

表1 算法复杂度及耗时比较

图12 雷达探测环境

由表2数据可知，在迭代初期，DOM相较于参照对比算法拥有较优的检测性能，而虚警性能相对较差。但是DOM通过迭代优化后，检测概率会稳步提升，虚警概率会迅速下降，从而获得更优的检测性能与虚警性能。

图13 实测RD谱

表2 实测的检测概率与虚警概率

6 结束语

本文提出了一种基于动态有序矩阵的外辐射源恒虚警检测算法，利用历史杂波数据来动态替换有序矩阵中的极值，使得杂波估计中值向理论中值收敛，通过估计中值求解检测阈值。仿真与实测结果表明，该算法在迭代初期拥有较优的检测性能，通过多次迭代可以快速达到检测概率与虚警概率的最优性能，在均匀杂波、多目标和杂波边缘的复杂环境中检测性能稳定，并且相较于同属时序类算法的CM-CFAR，拥有更优的抗目标干扰能力。