误差校正下单站多外辐射源BR/BRR多目标定位算法

左 燕 蒋陶然 陈志猛 彭冬亮

(杭州电子科技大学自动化学院 杭州 310018)

1 引言

外辐射源雷达利用第三方(广播、电视、卫星、通信基站等外辐射源)发射的电磁信号辐射源实现对“无线电静默”目标的探测与定位，具有隐蔽性高、抗干扰能力强、监视范围广、成本低等优点[1,2]。因此，近年成为雷达探测领域的研究热点。

外辐射源定位系统对目标监测通道的回波信号和参考通道的直达波信号进行相关性处理，得到时差和频差参数对目标进行定位[3]。外辐射源雷达采用双基/多基结构，时差对应外辐射源经目标反射至观测站距离和，即双基距(Bistatic Range, BR)，频差则对应双基距变化率(Bistatic Range Rate,BRR)[4]，联合BR和BRR可提高运动目标定位精度。

目前，目标辐射源联合时差/频差定位问题已进行了广泛研究[5-7]。而利用BR和BRR的外辐射源目标定位问题研究则相对较少。基于BR/BRR的外辐射源目标定位求解过程就是从非线性BR和BRR方程中解算出目标位置和速度，它本质是一个高维非线性优化问题。极大似然(Maximum Likelihood,ML)估计建立目标位置和速度的似然函数，理论上是最优估计。迭代ML算法通过迭代搜索获得目标参数估计，算法性能受初值影响[8]。随后一系列代数解算法相继提出，包括两步加权最小二乘(Two-Stage Weighted Least Squares, 2WLS)[9]、三步加权最小二乘(Three-Stage Weighted Least Squares,3WLS)[10]、约束总体最小二乘(Constrained Total Least Square, CTLS)[11]。

基于BR/BRR单站多外辐射源运动目标定位需要来自同一目标的所有量测值是无偏的。由于外辐射源之间信号发射时钟不同步，存在时钟偏差[12]；受信号阻塞和多径影响，外辐射源参考信号的路径和直达波路径不一致[13]；同时雷达观测站存在固有系统偏差等因素使得实际多基外辐射源定位系统中BR和BRR量测存在固定偏差[14]。忽视偏差的影响会导致目标定位性能严重下降，甚至产生虚假目标。文献[14]提出外辐射源BR定位下误差校正，随后文献[15]设计了外辐射源BR/AOA联合定位下误差校正算法。目前尚无外辐射源BR/BRR运动目标定位下误差校正研究。对此，本文首次提出了一种基于后验迭代关联最小二乘的BR/BRR多运动目标定位和误差校正新算法。与文献[14]和文献[15]不同，本文主要创新点包括：(1)建立了目标参数和BR/BRR偏差联合估计新模型；(2)利用辅助变量与目标参数之间的关联构造了新的等式方程，避免开方运算；(3)推导了BR/BRR联合定位和偏差估计克拉美罗下界(Cramer-Rao Lower Bound, CRLB)，并分析了算法估计理论误差和全局收敛性。

2 BR/BRR联合定位问题

假设由M个外辐射源和1个观测站构成的单站多外辐射源雷达对P个运动目标定位。不失一般性以观测站位置为原点 Sr=[0,0]T建立量测坐标系。

目标p 到观测站的距离和距离变化率分别为

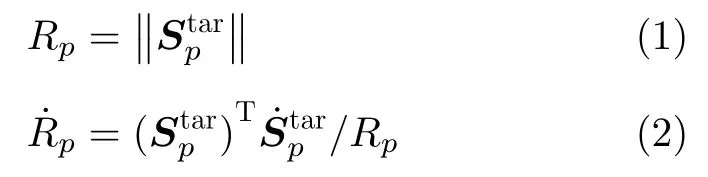
目标p 到 外辐射源m 的距离和距离变化率分别为

目标到达观测站和外辐射源的双基距BR和双基距变化率BRR的观测方程分别为其中，d0m,p=Rp+rm,p和 d ˙0m,p= R˙p+ r˙m,p分别为BR和BRR真实值，Δ dm和Δ d˙m分别为BR和BRR固定偏差，ndm,p和 nfm,p分别为BR和BRR量测噪声。

将上述BR和BRR观测方程描述为矩阵形式

外辐射源BR/BRR联合定位和误差校正问题是一个高维非线性优化问题，它根据多组BR和BRR观 测值联合估计目标位置和速度，以及固定偏差。

3 误差校正下目标定位算法

3.1 目标参数和固定偏差联合估计

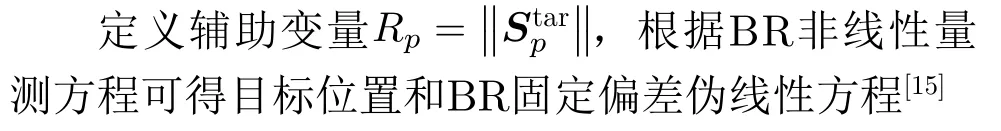
将式(9)和式(10)联立，其矩阵形式为

式(11)的加权最小二乘解为

式中，权重W =E[BeeTBT]-1=(BQBT)-1。

采用摄动分析方法，计算估计误差协方差为

3.2 关联最小二乘估计

上述估计过程假设辅助变量 Rp和与目标位置和速度变量相互独立，忽略了变量之间的关联性。为了进一步提高目标定位精度，建立关联最小二乘(Dependent Least Squares, DLS)估计模型。

根据式(1)和式(2)辅助变量的定义，可得

其中

则关联最小二乘估计解为

采用摄动分析法，计算估计误差协方差为

3.3 误差校正下迭代后验估计

将固定偏差估计值Δ dm和Δ d˙m代入BR和BRR量测方程进行校正。根据校正后的BR和BRR进行迭代后验估计，第l +1次迭代量测信息为

最后，获得BR和BRR固定误差估计值为

步骤(b) 根据式(21)和式(22)校正BR和BRR量测值，令k =0 ，l =l+1，转步骤2。

步骤(c) 根据式(23)和式(24)计算BR固定偏差Δdm和BRR固定偏差Δ d˙m。输出目标位置和速度 ，以及BR和BRR固定偏差。

4 理论性能分析

4.1 估计误差协方差和CRLB

令观测向量 q =[dT, d˙T]T，目标状态向量为，估计向量θ =[rT,ΔdT,Δ d˙T]T，则θ 估计误差CRLB可以表示为

由式(20)和式(25)知，估计误差协方差和CRLB均为求逆形式。将式(20)求逆运算前的形式展开

(2) 采用误差校正下后验迭代估计，BR固定偏差和BRR固定偏差逐渐趋于零，则G′≈G，误差校 正后估计误差精度可达到CRLB。

4.2 收敛性分析

θ =[Star,,R,,Δd,Δ ˙d]T

式中，

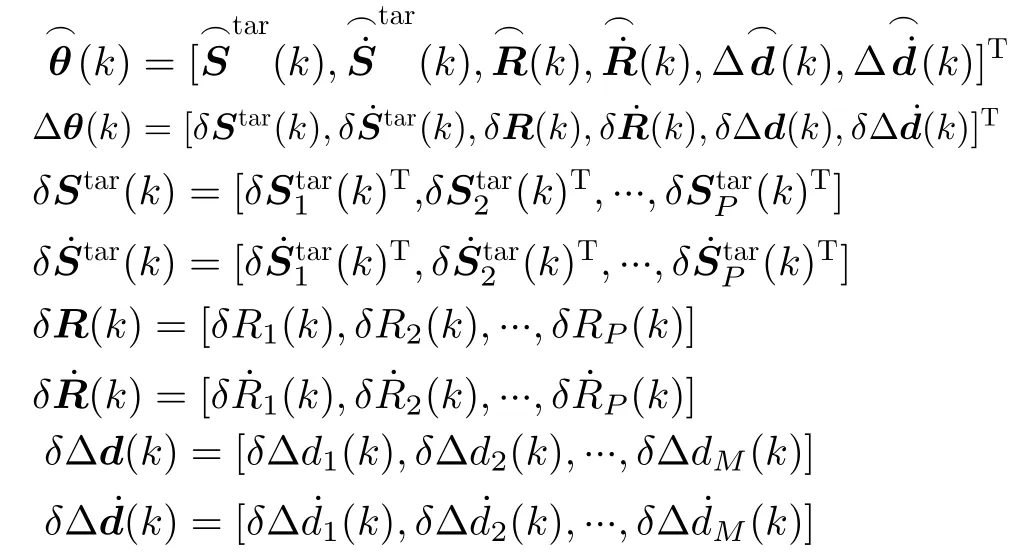
将式(34)代入式(9)和式(10)可得

将式(35)和式(36)写成矩阵形式

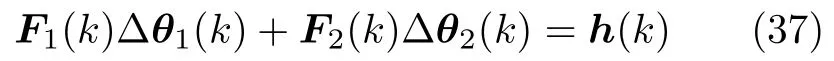
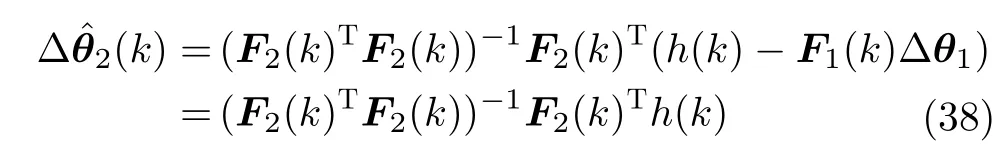
将式(38)展开，化为式(39)形式

5 仿真实验

本节通过仿真测试评估所提算法的定位性能，仿真场景设置[14]如下：场景中10个固定外辐射源，1个接收站，8个目标随机分布在 6 0 km×60 km的平面，空间几何分布图见图1。8个运动目标速度分别为(-0.3,0.1), (0.6, 0.3), (0.1, -0.2), (0.2, -0.2),(0.3, 0.5), (-0.2, -0.2),(-0.2, -0.2),(-0.3, -0.4), 单位为m/s。假设每对T-R组合能探测到所有目标。BR和BRR量测噪声分别服从零均值标准差为σd和 σf的高斯分布。BR和BRR的固定偏差分别为Δ d 和Δ d˙。进行蒙特卡罗仿真实验，蒙特卡罗次数设置为1000。

图1 目标-接收站-发射源位置

其次，研究不同量测噪声下目标定位性能。设BR和BRR固定偏差分别为30 m和3 m/s。量测噪声标准差 σe= [1, 10, 100, 400, 1000, 2000] m,BR和BRR量测噪声标准差分别为σd=σe, σf=0.1σe。将本文所提迭代后验DLS算法与迭代ML算法[8]比较，仿真结果如图3至图5所示。

图2 算法全局收敛率

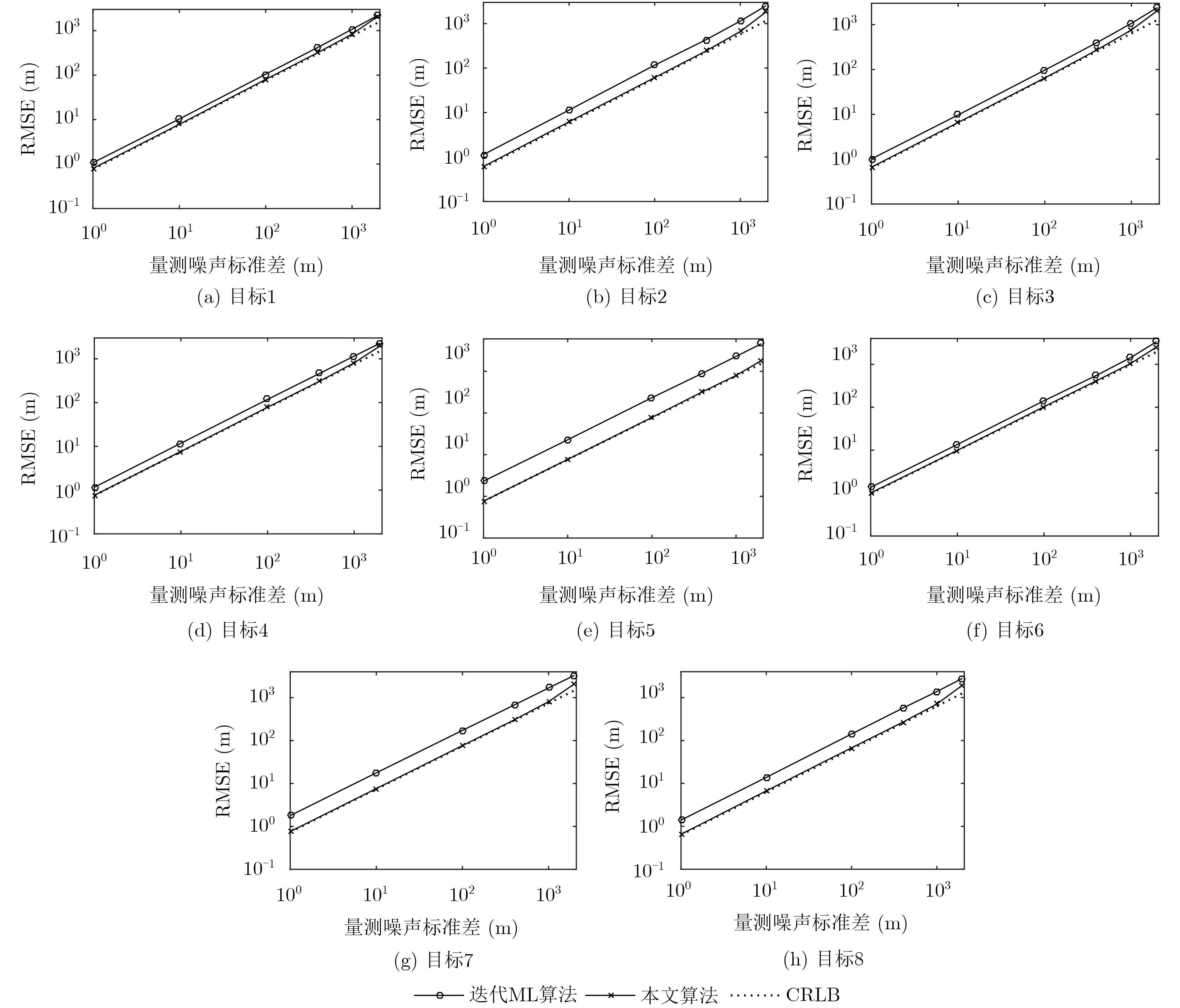
图3 不同量测误差条件下8个目标位置估计RMSE

图3和图4分别给出不同量测误差噪声下8个目标位置和速度估计误差RMSE。与迭代ML算法相比，本文算法对运动目标位置和速度估计精度更高，其RMSE达到CRLB。当σe大于1000 m时，本文算法开始偏离CRLB，其中目标5的定位误差RMSE略微偏离CRLB，原因是目标定位精度受“外辐射源-目标-观测站”的空间几何位置的影响。

图5给出不同量测噪声下BR偏差和BRR偏差估计误差RMSE。与迭代ML算法相比，本文算法误差校正精度更高。当 σe小于400 m时，所提算法估计性能接近CRLB。误差校正误差远小于量测误差，本文算法可实现较好的误差校正。

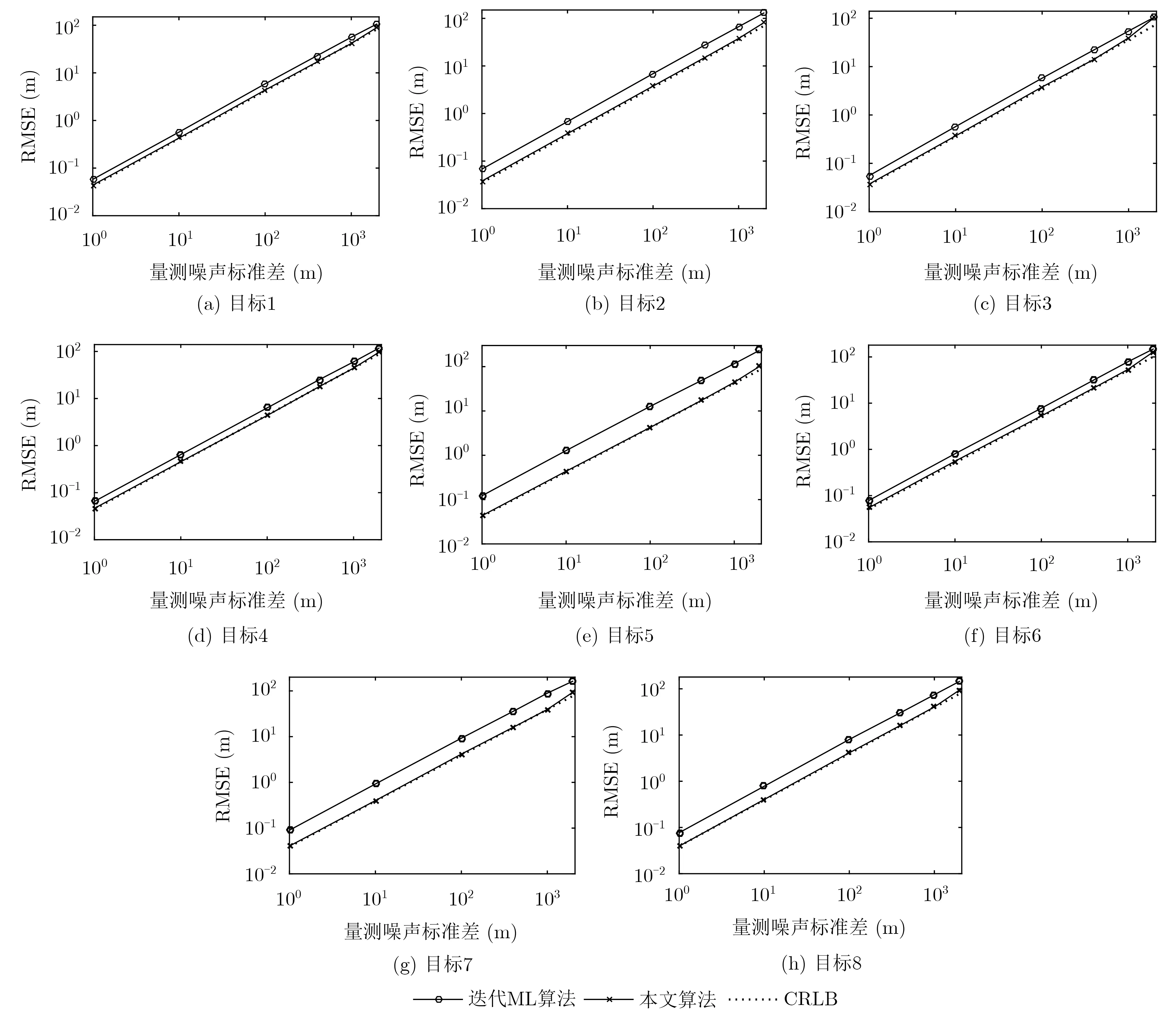
图4 不同量测误差条件下8个目标速度估计RMSE

图5 不同量测误差条件下固定偏差估计RMSE

6 结束语

本文研究了固定偏差下单站多外辐射源BR/ BRR多运动目标定位问题，提出了一种基于误差校正的迭代后验DLS算法。该方法选择合适的辅助变量建立多个运动目标参数和BR/BRR固定偏差联合估计新方程，利用辅助变量和目标参数的等式关系设计改进DLS算法，通过后验迭代进行误差校正进一步提高算法定位精度和全局收敛性。理论分析和仿真结果显示：

(2) 量测噪声较大( σe≤1000 m)时，本文算法目标位置和速度定位精度均能达到CRLB。

(3) 量测噪声适中( σe≤400 m)时，本文算法对偏差估计精度达到CRLB，实现较好误差校正。