距离相关噪声AOA协同定位下无人机路径优化方法

左 燕 刘雪娇 彭冬亮

(杭州电子科技大学自动化学院 杭州 310018)

1 引言

随着隐身飞机、反辐射导弹和电子对抗等技术发展，无源探测系统具有不主动发射电磁信号、隐蔽性好、覆盖范围广等优点[1]，已广泛应用于目标跟踪、监视、导航和无线通信等领域。

在无源探测系统中，角度信息(Angel Of Arrival,AOA)是基本的观测信息之一。基于AOA的定位跟踪算法相继提出，包括极大似然估计(ML)[2]、最小二乘估计(LS)[3]、伪线性估计(PLE)[4]、扩展卡尔曼滤波(EKF)[5]等。大量研究结果表明：AOA定位性能不仅取决于传感器量测精度，还与目标-传感器的几何位置有关[6]。当测角传感器(如红外传感器、光电设备、无源雷达)部署在多个无人机上，通过优化无人机(Unmanned Aerial Vehicles, UAV)位置可以进一步提高AOA协同定位性能[7]，AOA协同定位下无人机路径规划成为研究热点。

针对AOA协同定位问题，基于最大化FIM行列式指标(D准则)的最优几何分析[6]和UAV最优路径规划[7,8]相继提出。由于D准则可能导致大的估计偏差[8]，基于最小化CRLB的迹指标(A准则)下UAV路径规划随之提出[9,10]，通过非线性规划优化算法[11]在线计算满足各种状态约束和环境约束条件的UVA的轨迹，使跟踪目标状态估计接近CRLB。为满足无人机实时在线计算，参数化路径优化算法[12]被提出，该算法基于信息增益离线计算一组传感器-目标最优构型集合，在线选择最优UAV航迹，该方法只适合单个UAV。文献[13]采用归一化梯度算法计算UAV最优航迹，易陷入局部最优。

上述AOA协同定位问题假设量测噪声方差为常数，而理论[14]和实验[15]研究显示AOA量测噪声方差是距离的函数。文献[16]提出了一种联合最小二乘和非线性渐消滤波算法(LS-ISFEKF)。文献[17]基于广义CRLB(Generalized CRLB, GCRLB)[14]的迹最小化指标分析无约束下距离相关噪声AOA协同定位最优几何结构。文献[18]提出了一种距离相关噪声AOA协同定位下基于演化神经网络的UAV路径规划。不同于上述研究工作，本文主要创新工作如下：(1)提出了一种联合极大似然估计和变增益UKF滤波的定位跟踪算法，适应量测噪声方差随距离的变化；(2)基于GCRLB的迹最小化指标，分析了距离和角度约束下最优传感器几何构型；(3)考虑距离相关噪声特征，以最小化GCRLB的迹为目标函数，建立多约束UAV路径规划模型，结合罚函数和LM算法优化求解，兼顾性能和效率。

2 距离相关噪声AOA协同定位

在实际应用中测角传感器装载在多个UAV上，通过控制UAV运动方向使得传感器到达最佳探测位置，从而获得对目标更加精确的量测信息，减小定位误差。在传统UAV路径规划框架[7]的基础上，设计了距离相关噪声AOA协同定位方法总体框架(见图1)。给定距离相关噪声AOA量测，利用ML和变增益UKF获得目标状态的估计值，计算距离相关噪声AOA协同定位GCRLB指标。以GCRLB迹最小化为目标函数，建立多约束路径规划模型，结合罚函数和LM算法优化求解得到UAV的最优航向角，控制UAV运动到最优航路点。

2.1 距离相关噪声量测模型

2维空间下M个测角传感器分别部署在M个UAV上对目标定位。令目标位置Star=[xtar,ytar]T，速度传感器i的 位置Si=[xi,yi]T，速度则传感器i获得角度量测值

其中， θi为传感器i测 量的方位角，且- π ＜θi≤π。ni为 加性量测噪声，服从零均值，方差为高斯分布，即ni∼N(0,)。

在实际应用中，传感器方位角量测噪声方差与信号的信噪比SNR有关[14]。当传感器工作参数相同时，SNR仅取决于传感器和目标的距离，传感器i的量测噪声方差可以描述为[15]

图1 距离相关噪声AOA协同定位框架

2.2 目标运动模型

其中，Fk为 状态转移矩阵；ek为目标运动噪声，服从 均值为零，协方差为Q 的高斯分布。

2.3 ML-VUKF算法

考虑AOA量测噪声方差随目标-传感器距离变化特点，设计一种联合ML估计和变增益UKF算法(记为ML-VUKF算法)，具体如下：

(1) 初始值：采用ML估计算法[2]确定目标初始状态X ¯k|k。

(2) 生成Sigma点εnk及其权重wn

其中， N 为Sigma点的维数；λ 为标度参数，它确定围绕状态向量Xk均值的Sigma点的分布。

(3) 预测：计算Sigma点的一步预测，及相应量测预测值。

(4) 计算增益：根据目标一步预测值更新量测噪声方差，以此更新滤波器增益。

式(10)和式(11)中， R˜r为距离相关量测噪声方差。由于目标非合作，用目标一步预测值X ¯k+1|k代替目标位置真实值，计算 R˜r。利用式(12)计算增益，该值是目标-传感器距离的隐函数。

(4) 状态更新：根据新的量测更新目标状态和状态协方差。

3 GCRLB指标下最优传感器位置分析

3.1 GCRLB性能指标

考虑量测噪声与距离相关的特点，采用广义CRLB指标(GCRLB)[14]，以GCRLB的迹最小化为指标进行传感器和目标最优几何分布构型。

在高斯噪声假设下，距离相关量测噪声下AOA目标定位FIM为[14]

其中，

FIM的行列式为

GCRLB定义为FIM的逆[14]

GCRLB的迹为

3.2 无约束最优传感器位置分析

以GCRLB的迹最小化为定位性能指标，分析传感器-目标的最佳位置。将 A, B1和 B2具体形式代入式(24)，展开可得

式中，φij=θj-θi为 传感器i和 传感器j 的夹角。

(1) 给定任意距离 ri， 分析传感器最佳角度φij。最小化GCRLB的迹等价于优化问题

取sin 2φij=0,j /=i,i=1,2,···,M时，最 优 角度与距离 ri无 关，最优交会角为φij=±π/2(j /=i)。

(2) 给定任意角度 φij， 分析传感器i最佳距离ri。 将ai, bi, ci, di具体形式代入式(25)可得

上述函数f2(ri)随 着距离ri的减小而减小，因此固 定传感器之间夹角，传感器距目标越近越好。

3.3 约束最优传感器位置分析

考虑传感器最小探测安全距离约束以及UAV运动平台运动角度约束，分析角度约束和距离约束条件下传感器最优几何位置。

求导得到最优性条件

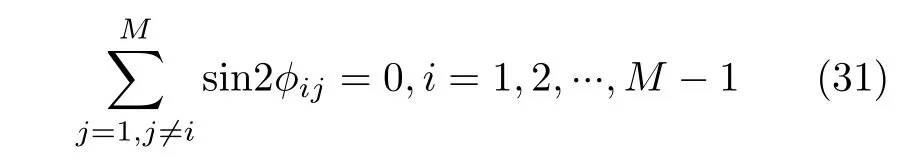
最优交会角为φij=π/M, GCRLB的迹最优值为

(1) 当π /2 ≤θmax-θmin≤2π时，最优性条件

(2) 当 π/M ≤θmax-θmin≤π/2 时， M个传感器最优分布满足式(33)的条件

(3) 当0 ≤θmax-θmin≤π/M时，对非线性目标函数(式(31))在区间[ θmin,θmax]进行梯度下降搜索[17]可 得最优传感器位置数值解。

4 AOA协同定位下UAV路径优化

在文献[7]的基础上，针对距离相关噪声特性，以GCRLB的迹最小化[14,18]为目标函数，考虑UAV运行过程中运动约束、通信和避碰约束、探测约束等，建立多约束AOA协同定位UAV路径规划模型。

其中， v 为UAV飞行速度，φi(k) 为 第i个UAV的航向角，φ (k)=[φ1(k),φ2(k),···,φM(k)]T; φmax为最大允许转弯率， rdmax为UAV对目标的最大安全探测距离，rsmax和rsmin分别为UAV之间最大安全避碰距离和最小通信距离；式(34)为目标函数；式(35)为UAV运动模型；式(36)为UAV转弯率限制；式(37)为UAV对目标最大安全探测距离约束；式(38)和式(39)分别为UAV之间最小通信约束和最大安全避碰约束。

该问题是带约束的非线性优化问题，通过构造罚函数将上述问题转化为如下无约束优化问题

无约束优化问题(式(40))可以采用梯度下降法[13]或牛顿法[7]迭代求解。牛顿法收敛快，但黑塞矩阵的逆求解时间复杂度高。梯度下降法时间复杂度低，但收敛速度慢，易陷入局部极小。本文采用LM算法[19]，它是梯度下降法和高斯牛顿法的自适应结合，当解远离最优值时梯度下降，在最优解邻域时快速收敛，满足动态场景的实时性。

5 仿真实验

仿真场景设置如下[7]：3个可移动传感器对1个目标进行定位。目标位置[10000, 3000] m，采样间隔T = 1 s。3个传感器分别装载在3个UAV平台。UAV1的初始位置为[1000, 1000] m, UAV2的初始位置为[2000, 0] m, UAV3的初始位置为[1000,-1000] m。3个UAV的运动速度均为40 m/s。UAV最大允许转弯率φmax=4°，UAV对目标的最大安全探测距离rdmax为20 km，UAV之间最大安全避碰距离rsmax为 7500 m，最小通信距离rsmin为200 m。所有UAV上部署精度相同测角传感器。考虑传感器测角量测噪声服从零均值高斯分布，且量测方差距离相关。3个传感器参考距离 r0为1500 m，参考距离对应的信噪比 SNR0为30 dB，路径损耗系数α为0.01。

首先，比较不同AOA定位跟踪算法。将本文所提ML-VUKF与ML-MEKF[5]和LS-ISFEKF[16]算法进行比较，蒙特卡洛次数为1000，图2给出不同定位跟踪算法下目标状态估计误差MSE比较曲线。

其次，研究相同精度测角传感器AOA协同定位下路径优化性能。将本文所提基于GCRLB的路径优化算法(记为本文算法)与基于CRLB的路径优化算法[7](记为优化算法[7])和常规直线轨迹飞行策略(记为直线轨迹)进行比较，图3至图5分别给出3种UAV路径优化算法下UAV飞行航迹，图6给出3种UAV路径优化算法下定位误差MSE比较曲线。

图2 不同AOA跟踪算法下估计误差MSE

图3 直线飞行策略下UAV飞行航迹

图4 优化算法[7]下UAV飞行航迹

图5 本文算法下UAV飞行航迹

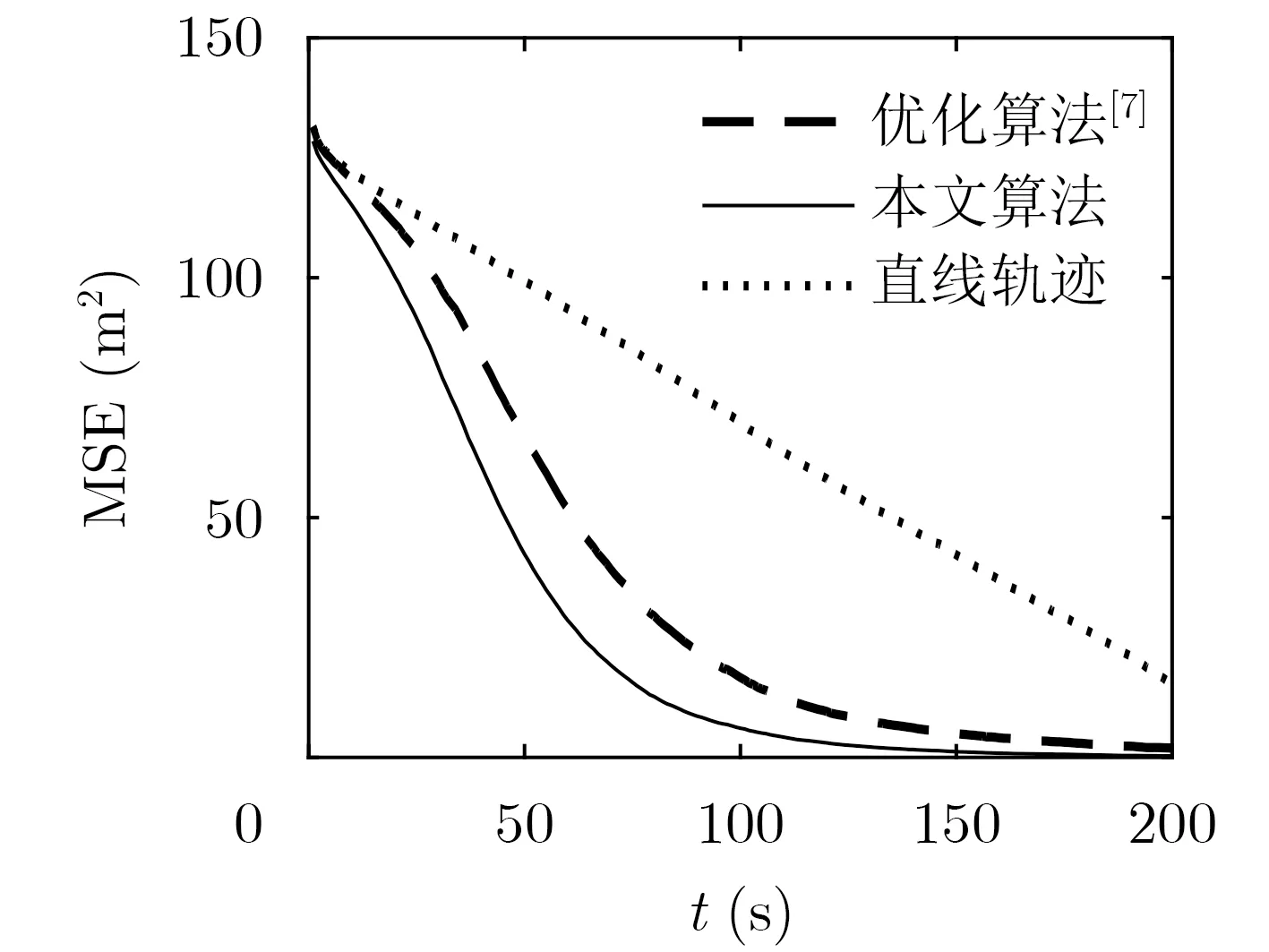
图6 不同算法下定位误差MSE

图7给出不同传感器个数下定位误差MSE比较曲线，随着传感器个数的增加目标定位误差MSE减小。对多个同类传感器组网，增加传感器个数有望提升目标定位精度。

最后，研究不同精度测角传感器AOA协同定位下路径优化性能。考虑不同精度的测角传感器，UAV1, UAV2和UAV3上部署的测角传感器在参考距离下的量测方差分别为 1°, 0 .8°和0 .1°。图8给出不同量测精度下AOA协同定位UAV下飞行航迹。将其余相同精度(均为 1°)测角传感器AOA协同定位下UAV飞行轨迹(见图5)比较，传感器测角精度 影响最佳传感器位置分布。

6 结束语

图7 不同传感器个数下定位误差MSE

图8 不同测角精度传感器协同定位下UAV飞行航迹

本文研究距离相关噪声AOA协同定位下UAV路径优化问题。首先针对AOA量测噪声方差随距离变化的特性，设计了一种ML-VUKF估计算法对目标定位。其次，基于GCRLB的迹最小指标分别分析了无约束和距离/角度约束条件下无人机和目标最优几何分布构型。最后，考虑UAV运行中实际约束建立UAV路径规划模型，并采用基于罚函数和LM算法优化求解。通过定位算法的改进和UAV路径优化，提高距离相关噪声AOA协同定位性能。理论分析和仿真结果显示：

(1) 给出了角度和距离约束下最优传感器位置分布：传感器和目标的最优距离为允许的最短距离rmin；当角度约束θmax-θmin≥π/M 时， M个传感器的最优交会角为 π/2 ；若θmax-θmin＜π/M，则采用迭代下降搜索算法在区间[ θmin,θmax]进行梯度下降搜索找到传感器最优位置数值解。

(2) 基于GCRLB迹最小化指标UAV路径优化策略下AOA定位性能优于基于CRLB迹最小化指标下路径优化算法[7]。传感器与目标的距离越近，量测噪声方差接近固定值，两者算法定位性能接近。传感器的个数增加可以提高AOA定位精度。

本文提出基于GCRLB的UAV路径优化问题为单步决策。考虑当前决策对长期定位性能的影响，开展基于GCRLB的多步决策下路径优化问题是下一步需要研究的工作。