基于策略学习的机票动态定价算法

卢 敏 张耀元 卢 春

①(中国民航大学计算机科学与技术学院 天津 300300)

②(中国南方航空股份有限公司信息中心 广州 510000)

1 引言

航空公司采用收益管理技术提升了2%至8%的票务年收入[1]。机票动态定价是收益管理的核心，旨在构建航班机票售价策略，将不同票价等级的机票适时地销售给不同的消费者，以实现收益最大化。

Gallego等人[2]使用强度控制理论求解了不确定需求下预期收入的上限。Otero等人[3]采用阶段类型分布和更新过程建模客户购买机票的时间及购买概率。Delahaye等人[4]通过细分商务和休闲旅客的不同价格敏感度进行动态定价。高金敏等人[5]研究了时变需求下动态定价模型。Selcuk等人[6]针对4种不同的价格需求关系提出了精确的动态规划方法。除了上述面向垄断市场环境的定价研究[1-6]，还有从竞争角度出发的定价研究[7,8]。Lin等人[7]构建了基于博弈论的实时价格预测模型。施飞等人[8]通过航空公司与旅客的动态博弈解决各等级票价的售票时间。

现有机票动态定价方法都建立在提前预测各票价等级的需求量基础之上。然而，实际应用中各等级票价的需求量受节假日、季节、售票时机等诸多因素影响。基于历史销售数据进行函数拟合的需求量预测方法存在预测偏差，降低了建立在需求量预测方法之上的模型性能。为此，本文提出基于策略学习的机票动态定价算法。其核心是不再直接预测各票价等级的需求量，而是从历史购票数据上学习具有最大期望收益的机票定价策略。在两趟航班两年历史销售数据上的多组模拟定价结果表明：相比于现行定价策略，策略学习算法的票务收益平均提升率分别为30.94%和39.96%，且比需求量预测方法提升了6.04%和3.36%。

目前存在将强化学习应用于收益管理领域的研究，如电动汽车[9]、广告竞价[10]、可再生能源管理[11]、机票超售及座位控制[12-15]。Gosavii等人[12]提出了面向超售和多等级票价的半马尔可夫决策模型。Shihab等人[13]采用深度强化学习优化航班座位控制策略。Qiu等人[14]建模了旅客行为驱动的航班定价。Lawhead等人[15]提出一种航班座位收益有界的动作评论算法。不同于上述工作，本文聚焦于采用离线强化学习求解机票动态定价策略。

2 航班机票动态定价算法

在机票销售期内以某票价等级出售机票，售票系统会得到立即收益，即座位销售数×票价等级×机票全价，同时减少航班剩余座位数。为了最大化后期座位收益，航班剩余座位数又影响下一时刻的机票定价。为此，机票动态定价受航班剩余座位数、定价策略和收益等相互影响，可建模为强化学习问题。

航班机票动态定价的强化学习要素分别为：(1)状态集 S 表示航班剩余座位数。设n 为某航班座位容量，航班在时刻t 的状态(剩余座位数)st∈S ={n,n-1,···,0} 。 (2)动作集 A表示所有的票价等级，本质为经济舱全票价的折扣率。航班在时刻 t采用的动作(票价等级)为 αt∈A 。(3)策略函数π (α|s)表示在状态s 下执行动作α 的概率。策略函数是算法的学习目标，使得算法根据它产生动作序列。(4)收益函数 r(s,α) 表示在状态s 下执行动作α 的立即收益，取值为p ×α×N ，其中p ,N分别为经济舱全价和销售的座位数。

引入动作值函数 qπ(s,α) 以 评估策略函数π(α|s)的好坏程度，见式(1)。式(1)的物理含义是给定状态s 沿着策略π 执行序贯性决策后预期总折扣奖励。

其中，P r(st+1|st=s,at=a)表 示在状态st下执行动作 at后 跳转到状态st+1的概率。由于机票销售过程无法建模上述转移概率而仅可观察剩余座位数st+1，采用时序差分法[16]更新动作值函数。

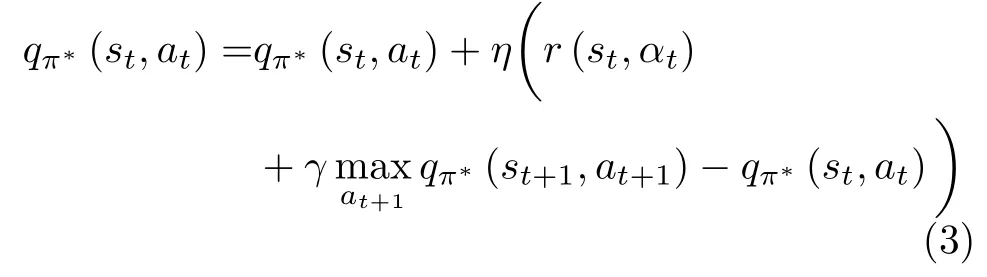
其中， η表示学习速率。当动作值函数通过更新达到收敛后，每个状态s 在最优策略π∗的 动作π∗(s)为

由于航班动态定价的状态空间和动作空间都离散且有限，提出基于策略学习的机票动态定价算法，见表1。算法首先初始化一个2维矩阵Q-table以表示动作值函数 q (s,α)，其中矩阵的行数为状态空间数| S|， 列数是动作空间数| A|。其次，在航班的第1天到 T -1天的历史销售序列上依次据式(3)和式(4)进行策略 π的评估和改进。重复上述循环操作 ，直至算法达到预先设定的最大迭代次数。

3 实验

3 .1 实验设置

3.1.1 数据集

实验数据集是航班历史机票销售序列，是由2010年1月1日到2011年12月31日的民航旅客订票日志PNR (Passenger Name Record)生成的。一条PNR是一次订票信息，主要字段包括旅客身份证号码(信息加密)、航空公司、航班号、出发机场和到达机场(机场三字码表示)、订单编号、票价等级等，示例见表2。

表1 机票动态定价策略学习算法

折中于算法在民航旅客订票日志上所有航班的运行时间，以及评价航班每一天动态定价策略，挑选在航线热度、经济舱总数、实际销售等方面差异较大的两个航班CA1501和JR1505进行实验，其统计信息见表3。民航旅客订票日志中票价等级的精度为0.0001，且各票价等级销售的机票数比较稀疏。意味着很多二元组(剩余座位数，票价等级)未在历史数据中出现，使得这些元组对应的动作值函数无法更新，导致后期动态定价存在较大的偏差。比如航班CA1501历史销售轨迹中产生了5737种票价等级，而各票价等级产生平均机票数为22.68，这表明动作值函数矩阵Q-table中某一列平均至少有255-22.68个元素未被更新，累计有5737×(255-22.68)个元素未更新，其中255是航班CA1501的总座位数。精确度为千分位也会产生类似的结论。为此，实验中将票价等级精度降至百分位，并在实验中分析万分位精度对航班座位收益的影响。

3.1.2 评价指标

为评价航班动态定价策略好坏程度，定义航班收益平均提升率ALR@T(Average Lift Rate at T days)：

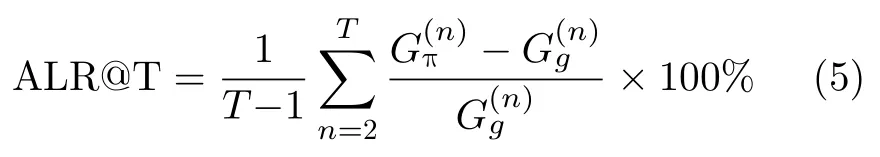
3.1.3 基准算法

(1)航班现行定价策略

(2)票价等级需求量预测方法

表2 旅客订票记录示例

表3 实验数据集的统计信息

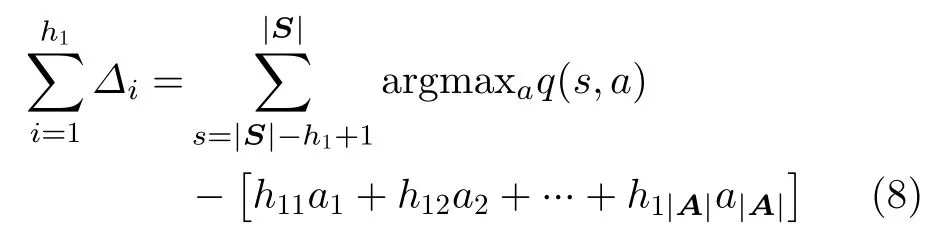
其中，| S|为 航班总座位数。依式(8)计算m 个周期的收益差，需求量预测方法和策略 π 在第n 天航班收益差为

3.1.4 参数设置和运行环境

航班CA1501和JR1505经济舱总座位数 N分别为255和52。算法需预先设置的参数分别为：学习速率 η =0.2,0.4,0.6,0.8 、折 扣 因 子γ =1、算 法 总迭代次数e pisodes=5000。算法硬件环境为Intel(R)Xeon(R) Silver 4110、主频3.4 GHz、内存126 GB。实 验训练共耗约142 h。

3.2 实验对比及分析

3.2.1 航班 CA1501实验结果

在航班CA1501进行了717组实验，其结果见图1(a)。相比于现行定价策略，动态定价策略 π的收益平均提升率A LR@T为30.94%；相比票价等级需求量预测方法，平均提升率为6.04%。

图1(a)中动态定价策略 π相比于现行定价策略的提升率曲线-策略πvs现行定价策略-可分为4段。在2010年1月2日到2010年2月10日，1月1日至1月3日票务收益较差，使得学习后的策略收益也低。1月4日收益较1月3日增长了115%，算法能快速学习此定价策略以用于后续定价。故此阶段内曲线出现骤增，平均提升率 ALR@T稳定至约35%。在2010年2月11日到2010年2月19日曲线出现第2次骤增，其原因是：2010年2月11日为农历腊月二十八，出现“倒春运”，即机票销售数和价格都明显下跌，期间平均收益仅为整体的32.29%。然而，定价策略π 是从2月11日之前销售数据上学习，导致策略 π的机票价格要高于“倒春运”期间价格，出现较大收益差值。第3段为2010年2月11日到2011年1月30日，曲线逐渐降低并趋于平稳，收敛至约21%。其原因是：在大量历史数据上的学习，动态定价策略与现行定价策略的收益差值逐渐减小。最后一次曲线提升发生在2011年2月1日，其原因是：2011年2月1日为农历腊月二十九，也出现“倒春运”，因在大量历史数据上的学习避免了类似第1次突变，趋于平稳。

图1(a)也列出了定价策略 π相比于需求量预测方法的提升率曲线-策略 πvs需求量预测方法。实验初期因训练数据较少，动态定价策略产生的收益低于需求量预测方法。随着训练数据的增加，策略学习方法与需求量预测方法的收益差距逐渐减小，曲线平稳提升并趋于稳定，最终收益平均提升率 为6.04%。

3.2.2 航班JR1505实验结果

相比于航班CA1501，航班JR1505收益更易受定价影响。航班JR1505上的610组实验结果见图1(b)。动态定价策略 π相比于现行定价策略和需求量预测方法的收益平均提升率 ALR@T分别为39.96%和3.36%。

从图1(b)可知，动态定价策略 π相比于现行定价策略的提升率曲线-策略 πvs现行定价策略，主要可分为3段。2010年1月26日到2010年11月10日为第1个增长期。定价策略 π通过不断学习以往经验，平均提升率A LR@T逐渐提升，在4月20日趋于平稳，收敛至25%。第2个增长周期发生在2010年11月2日，其原因是：航班JR1505在此后一个月机票销售收益较前一月平均降低了43.80%，使得收益差值增加，曲线逐渐上升。第3个拐点发生在2011年4月20日，其原因是：航班由淡季转为旺季，此后一月较上月收益提升41.22%。实际收益的提升使得差值逐渐减小，曲线回落并重新收敛至39%。此外，相比于需求量预测方法，策略学习方法随着不断学习，平均提升率 A LR@T平稳提升并趋 于稳定，最终收敛至约3%。

3.3 票价等级精度对收益的影响

表4表明不同的票价等级精度产生不同规模的票价等级，为此分析票价等级精度对算法性能的影响。表4列出2011年6月22日航班CA1501在票价等级精度为0.0001和0.0100的实验结果。万分位精度产生了4590个动作，而百分位精度缩减至120个动作。百分位精度较万分位在平均提升率 A LR@T上提升3.17%。

分析算法在精度为0.0100时性能提升的原因。图2(a)列出票价等级精度分别为0.0100和0.0001时定价策略 π在各状态上的票价等级差值。统计表明，不同精度下的模型在所有状态上采取的票价等级总体相差不大，票价等级差的均值为0.05，方差为0.006。仍有部分点波动较大，造成收益差距。图2(b)以波动点-剩余座位数196为例分析。当精度为0.0001时，采取的票价等级为0.8453，落在区间(0.84,0.85]频数为8。当精度为0.0100时，采取的票价等级为1.04，落在区间(1.03,1.04]频数为65。为此，精度为0.0100更易捕捉具有明显集中趋势的“众数”票价等级，以代表此状态下整体票价水平 ，而非选择出现频次最高的单一票价等级。

3.4 学习速率的影响分析

学习速率η 影响着算法的收敛速度和定价策略的收益，以2011年12月31日航班CA1501为例分析学习速率的影响。图3(a)指出学习速率为0.2, 0.4,0.6, 0.8时，算法收敛的迭代次数依次为4860, 2167,1274, 788。因此，经验上学习速率在0.2以上就能保证算法收敛。图3(b)指出算法在5000次迭代时，增大学习率不会对收益平均提升率 A LR@T产生影响，其中计算 A LR@T的基准算法为航班现行定价策略。

表4 票价等级精确度影响分析

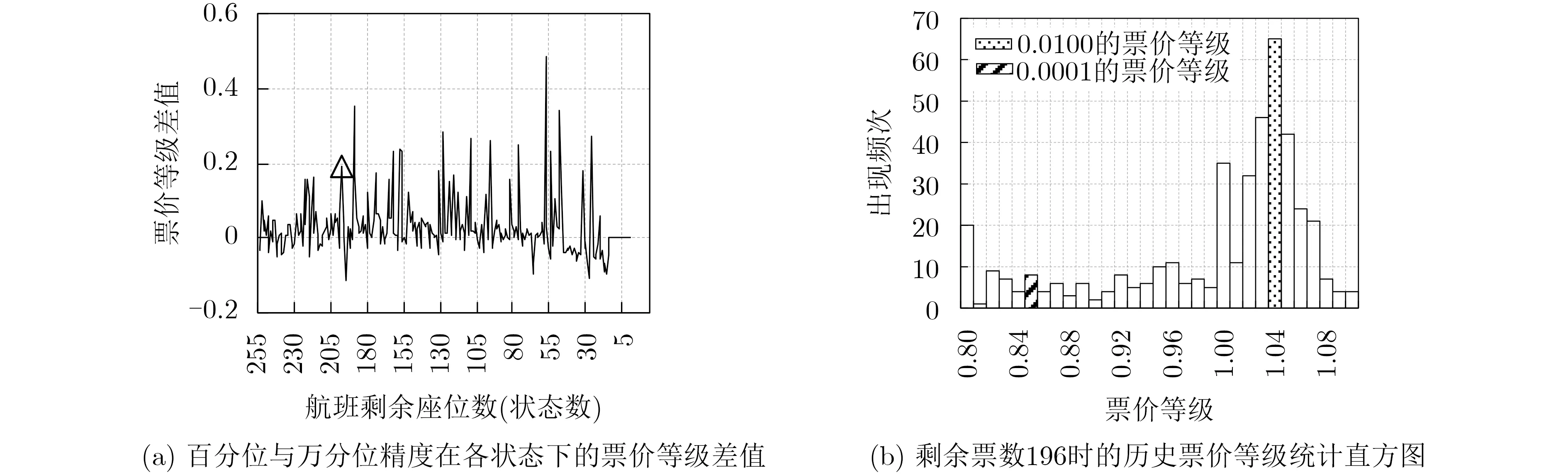
图2 2011年6月22日航班CA1501在精度为0.0100和0.0001下的实验对比

图3 学习速率对算法性能的影响

4 结论

针对航班票价定价过程中航班剩余座位数与机票价格相互影响，提出了基于策略学习的机票动态定价算法。算法通过定价策略评估和策略更新，输出具有最大期望收益的机票动态定价策略。在海量民航旅客订票日志上两个航班的多组模拟定价结果表明：相比于现行机票销售策略和需求量预测方法，算法在收益平均提升率上有显著的提升。后续将对航班状态的时序特征展开研究。