基于球面Haar小波和卷积神经网络的飞行员虹膜识别

贾 博 冯孝鑫 李 军 俞碧婷 赵 倩 吴 奇*

①(东航技术应用研发中心有限公司 上海 201707)

②(上海交通大学电子信息与电气工程学院 上海 200240)

③(伍伦贡大学 澳大利亚 伍伦贡 2500)

1 引言

随着机器视觉的不断发展，各种新兴的生物识别技术开始出现并得到广泛应用，虹膜识别就是其中很有代表性的一种。由于虹膜识别具有唯一性、稳定性、安全性等优点，以及虹膜作为眼球的一部分，一般情况下不会受到损坏，相对于其他生物识别技术来说具有较高的优越性，因此广泛应用于如移动支付、门禁系统以及智能手机和计算机的解锁等涉及身份信息确认的众多场景。但是传统虹膜识别由于拍摄和图像转换等原因准确率并不高，如何提高虹膜识别的准确率和识别速度就成为热门的研究话题。显然，提高虹膜识别有两种有效途径：一是提取更加有效的虹膜特征，二是建立更为有效的分类器。本文的出发点在于，提取一种更加新颖的虹膜球体表面特征，获取更加精细的虹膜球体局部信息。

2002年Ma等人[1]提出使用一组Gabor滤波器来捕获局部和全局虹膜特征，设计一种基于加权欧几里得距离的虹膜特征识别方法，该方法显著改善了识别精度与模型运行时间。Yao等人[2]提出了一种基于改进的Log-Gabor滤波器的虹膜识别算法。由于具有严格带通的特性使得Log-Gabor滤波器比复杂Gabor滤波器更适合于提取虹膜相位特征。Nabti等人[3]采用多尺度边缘检测方法作为预处理步骤以有效地定位虹膜，并提出了一种使用矩不变量的特征向量表示和基于异或运算的快速匹配方法。2012年，Proença等人[4]提出一种基于虹膜颜色和形状的多特征融合识别方案，实现无噪声虹膜动态划分。Santos等人[5]提出1维小波、2维小波、Gabor、局部二值模式(Local Binary Patterns, LBP)和尺度不变特征转换(Scale-Invariant Feature Transform, SIFT)的多特征融合的虹膜识别方法，识别结果得到了显著改善。Tan等人[6]提出结合虹膜纹理、虹膜颜色、皮肤纹理和睫毛分布的虹膜识别方法。这种方法包含了虹膜外部有效特征，但也使得运算更为复杂，且易受干扰。2015年Huo等人[7]提出一种融合Gabor滤波器和直方图变换的虹膜识别方法，该方法也获得了良好的识别效果。2016年Kumar等人[8]提出一种基于2维离散余弦变换(Discrete Cosine Transform,DCT)的虹膜特征提取与识别算法，其中2维DCT可以用于提取虹膜上最具区分度的特征。2019年刘元宁等人[9]使用2维Haar小波提取虹膜纹理特征作为频域特征并与使用二分统计局部二值模式提取的空域特征相结合，提出一种特征加权融合的虹膜识别算法。将Gabor滤波与Haar小波相结合，提取虹膜特征实现虹膜2次识别的方法也能取得较好的效果。

上述方法在不同数据集上都取得了不错的虹膜识别效果，但是这些研究大多使用虹膜平面图像信号，未曾涉及虹膜球体表面信号。虹膜是一种复杂球状体，其表面是一种复杂曲面，而不是一个平面。曲面的几何特征信息是虹膜图像的有效特征信息。显然，研究一种可以表达球体表面信号的方法对于虹膜识别至关重要。球面Haar小波基(Spherical Haar Wavelet, SHW)具有球状表面信号分析能力[10]，而目前比较有代表性的SHW主要有以下3种：

第1种是以Bio Haar小波基为代表的半正交球面Haar小波基，其对于平滑的函数和信号具有较好的处理能力，利用其定位特性，可以简单高效地实现很多球面图像处理算法，比如局部平滑和增强。但由于其为半正交小波基，不能使用K最大近似策略(K-largest approximation strategy)得到最佳近似，因此与其他正交或几乎正交(nearly orthogonal)的小波基相比，寻找Bio Haar小波基的最佳近似会更困难。

第2种为以Pseudo Haar小波基为代表的伪Haar小波基，其并不是L 2(S2,dω)空间中的基，与真正的球面Haar小波基相比，伪Haar小波基并不需要在运行时计算滤波系数，其滤波系数始终与平面的非标准Haar小波相同。伪Haar小波基不能表示较小的细节信息，与正交基和几乎正交基相比，在近似球面信号时效率更低。

第3种是以Nielson和Bonneau小波基为代表的几乎正交球面Haar小波基。当球面三角形域逐渐变为平面时，该类型小波基变为完全正交的小波基，其解决了对称性和完全正交性无法同时实现的问题，同时与Bio Haar小波基相比，在相同的分解尺度下以及使用相同比例的小波系数时，均方根误差更小，在提升了效率的同时计算复杂度并没有增加。但当球面三角网络细分层度较低时，其正交性较差，此时使用其近似球面信号误差较大。

由此可见，大部分球面Haar小波基都不可避免地存在各种缺点，无法保证在各种条件下对球面信号的分析和近似表示始终保持较高的精度。因此，本文聚焦一种正交对称的球面Haar小波基，它可以有效表示虹膜球体表面信号。目前，对正交对称的球面Haar小波基的研究很少见报道。它可以处理复杂拍摄条件下出现曲面扭曲，以及无法获得很好的特征表示等问题。

显然，发展正交且对称的球面Haar小波基对于虹膜识别是一种全新的特征提取方法，具有重要理论意义和巨大的应用价值。正交对称球面Haar小波(Orthogonal and Symmetric Spherical Haar Wavelet, OSSHW)基是以球面内接正八面体为基础使用球面三角形划分球面，并在此基础上构建一种离散的OSSHW基。本文提出一种基于正交对称的Haar小波和卷积神经网络的飞行员虹膜识别方案。使用OSSHW得到的虹膜特征输入卷积神经网络中进行识别，如图1所示。

图1 仿真实验流程图

本文的结构如下：第2节给出球面谐波函数以及各类球面Haar小波基；第3节给出正交且对称的球面Haar小波基的定义与推导过程；第4节给出仿真实验，使用球面谐波函数以及5种不同的球面Haar小波基对球面虹膜信号进行处理，提取虹膜特征，并使用构建深度学习网络实现对虹膜特征的识别，对比球面谐波函数和这些球面Haar小波基的优点与不足；第5节是结论。

2 球面Haar小波基与球面谐波函数

2.1 球面Haar小波基

2.1.1 Bio Haar小波基

考虑由测地球体构造形成的球面三角形Tj,k⊂S2,k ∈K(j)， 若α (Tj,k) 为三角形的球面面积，则定义尺度函数和双重尺度函数为

其中，χTj,k为特征函数。对于一般化的Haar小波的构造，本文只需要考虑一个确定的三角形 Tj,∗的子三角形 Tj+1,l=0,1,2,3，将这些基称为Bio Haar函数。小波函数(m=1,2,3)为

2.1.2 Nielson小波基

Nielson小波基是定义在嵌套三角形域上的Haar小波基，其主要特点为“几乎正交”，即当球面三角形域逐渐变为平面时，小波基变为完全正交的小波基。由于小波基的正交性在计算最佳近似时十分重要，在这方面，完全正交的小波基优于半正交小波基，具有几乎正交特性的Nielson小波基就是对半正交小波基的改进。

2.1.3 Bonneau小波基

Bonneau小波基针对Nielson小波基做了改进，Nielson小波基的重构矩阵各项为关于子三角形面积的2次项，Bonneau小波基同样为几乎正交的，但重构矩阵具有更低阶次的系数多项式。

2.1.4 Pseudo Haar小波基

Pseudo Haar小波基根据最优三角Haar小波基构造，球面小波基于测地线构造得到，使用测地平分线划分球面三角形。为在细分层l 的第i个三角形。对于第l层，定义第i个尺度函数(ω)为

l Tli

定义3种在第层与 相关联的小波函数为

2.2 球面谐波函数

球面谐波函数为球坐标下3维拉普拉斯方程角度部分的解，经过归一化后，球面谐波函数可以使用伴随勒让德多项式来表达，即

定义在球面上的函数f (θ,φ)可以使用球谐函数与系数的线性组合方式来表达，即

为研究球面谐波函数对于球面信号处理的能力以及使用球面谐波函数提取虹膜特征并用于虹膜识别的效果，本文尝试使用球面谐波函数对球面虹膜信号进行分解和重构，重构后的函数作为原球面虹膜信号的近似，对该近似球面虹膜信号进行可视化，从而可以直观地展示球面谐波函数对球面信号处理的效果。

对球面上的每一个采样点上通过求解伴随勒让德多项式来得到对应的一系列球面谐波基函数的函数值。将每一个采样点从球面坐标映射到2维纹理坐标中，有效地避免纹理扭曲现象，使用映射后的2维纹理坐标获取输入图像的采样点对应的信号值，使用蒙特卡罗积分估算法得到球面谐波基函数与原函数积分的近似值，从而获得系数。

根据球面谐波基阶数不同，获得的球面谐波系数的数量也不同，从而使用球面谐波系数对原信号进行近似重构时，效果也相应不同。重构原信号使用如式(7)

实验中使用虹膜图像作为原始信号，使用球面谐波函数对原信号进行分解，提取球面谐波系数，并使用球面谐波系数进行近似重构，并对重构出的函数进行可视化。

根据图2所示的重构图像可以看出，随着球面谐波基阶数的增加，重构出的球面信号具有越来越多的细节信息，但在阶数为60时，球面谐波系数已经有 6 12=3721个，重构出的信号与阶数为80时的重构信号相比，仍然丢失了很多高频细节，从而可以看出球面谐波函数在处理高频信号时的不足。在虹膜识别时，如果使用球面谐波函数进行虹膜图像的特征提取，虹膜中的很多细节纹理信息会丢失，而且形成的特征码维度会非常大，不利于后续的识别和处理。

图2 球面谐波函数重构图像

3 OSSHW小波变换

3.1 划分方案

OSSHW小波基定义在P={Tj,k|j ∈J,k ∈K(j)}上，位于最粗糙层级上的域T0,k由一个各面为三角形的多面体向球面投影得到，位于下一层级的域由4部分的细分形成。因此每一个 Tj,k具有4个子域。

子域通过在组成Tj,k的每一条边上插入一个新的顶点得到，因此，位于最粗糙层级的域T0,k是划分树集合的根节点，而P 由这些树的并组成。

与Schröder和Sweldens的划分方法不同，OSSHW小波基并未使用测地平分线来确定新的顶点的位置，而是通过保证3个外部的子三角形,和具有相等的面积来划分。这同时也是保证小波基同时具有正交性和对称性的关键。

3.2 尺度基函数

对于一个类Haar基，尺度基函数φj,k在其支撑区域Tj,k上为常数，因此

其中，ηj,k为归一化常数，使得尺度函数满足

根据 Tj,k的不相交性，对于确定〈的j，同在〉第j层的尺度基函数相互正交，即φj,k,φj,k′=0,k /=k′。根据在S2上的内积的定义，求得归一化常数和尺度函数分别为

图3 球面三角形划分方案

根据尺度基函数性质，得滤波系数为

3.3 OSSHW小波基函数

根据快速小波变换的理论，小波合成步骤可以通过如式(14)的矩阵形式表示

根据尺度基函数的性质，每一个第 j层的尺度基函 数φj,k都 可以写为第j +1 层 的尺度函 数φj+1,l的线性组合的形式，即

同时第 j 层的小波基函数ψj,m同样可以写为第j+1 层的尺度函数φj+1,l的线性组合的形式，即

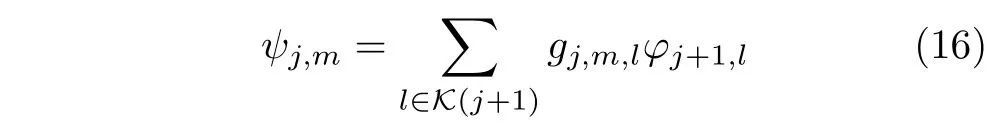
从而可以看出，若要求小波基满足半正交性，即需满足尺度函数与小波函数内积为0，若要求小波基满足正交性，即需满足两个不同的小波函数内积为0，根据内积的线性性质，则滤波系数需满足如式(17)的条件

在此基础上需满足外部3个子三角形面积相等的条件，此时，合成矩阵满足对称性，合并上文中推导出的小波基的半正交性以及正交性的条件，列出如式(18)的两个等式

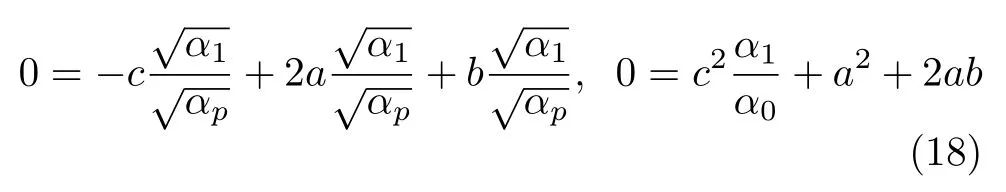
假定c =1，求解式(17)和式(18)两个等式可以得到OSSHW小波的小波基函数为

3.4 OSSHW实验分析

为比较各类球面Haar小波基近似球面信号的效果，分别使用Bio Haar小波基、Nielson小波基、Bonneau小波基、Pseudo Haar小波基以及OSSHW小波基对相同的输入信号进行小波变换，使用相同数量的系数对原信号进行最佳近似重构，其中，除半正交基Bio Haar小波基外，其余小波基均可以使用K最大近似策略得到最大的 k个系数即可。将重构后的信号与原信号进行比较，分别计算l1和 l2范数误差，得到不同小波基的误差随使用系数数量k 变化的情况，并绘制图像进行比较。

图4给出了虹膜信号不同球面小波基的两个范数误差与保留系数的关系。由于这些小波基的重构误差相对接近，因此横坐标使用对数坐标轴，以使曲线易于区分和对比。可以看到OSSHW小波基在细分层数为7时误差与Nielson, Bonneau和Pseudo Haar小波基非常接近。在 l2范数误差中，OSSHW小波基的重构误差小于其他小波基。4个小波基中，Nielson和Bonneau小波基的重构误差基本相等，随着保留系数数量的增加，它们的重构误差逐渐接近于OSSHW小波基。Bio Haar和Pseudo Haar小波基具有更高的重构误差。在 l1范数误差中，Bio Haar小波基的重构误差明显较高，其他4个小波基的误差基本相等。显然，OSSHW小波基对虹膜图像有部分优势。

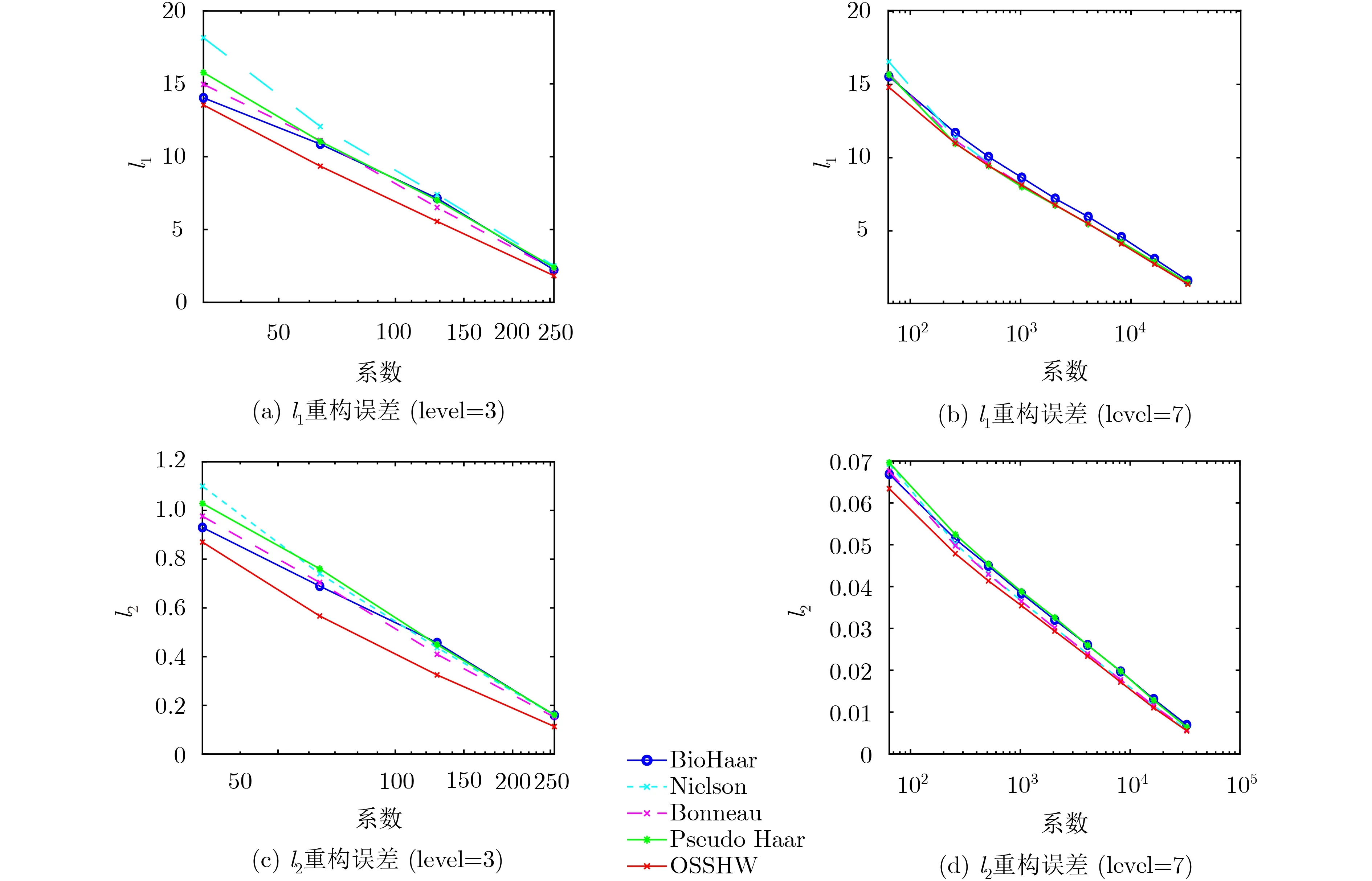
图4 虹膜信号重构误差

对于作为球面信号的虹膜图像，当细分层数为3时，小波基之间的差异显著增加。Nielson和Pseudo Haar小波基的 l1和l2范数误差较大，Bio Haar和Bonneau小波基的误差较小。随着保留系数的增加，除OSSHW小波基之外的4个小波基误差逐渐接近并且仍然高于OSSHW小波基。显然，OSSHW小波基比其他4个小波基更具优势。

表1给出了使用5种不同球面Haar小波基进行虹膜信号重构l2误差。表中数据为使用5层球面细分层数保留1.56%的小波系数时各类小波基的重构误差，可以看到，OSSHW与其他4种小波相比，误差更小，具 有更好的提取并近似球面信号精细特征的能力。

4 仿真

4.1 虹膜图像预处理

实验中使用的虹膜图像部分来自IITD虹膜数据库，另一部分为使用数字CMOS相机采集的东方航空公司飞行员的虹膜图像。由于采集到的虹膜图像通常包含眼睑、睫毛等眼睛的其他部位，同时也包含如拍摄过程中由于反光导致的瞳孔中的亮点等噪声干扰。因此在使用小波变换提取虹膜特征以及识别之前需要对虹膜图像进行预处理，保留虹膜纹理信息的同时尽可能地去除干扰因素。

首先需要对虹膜进行定位，即在一张虹膜图像中确定虹膜的内外边界以及瞳孔的位置。对于虹膜的内外边界，使用Canny边缘检测与Hough变换[12]来确定对应的边界圆。其中，为减小Hough变换的计算量，加快其运算速度，选择合适的比例系数按比例将原图像缩小。之后对虹膜图像进行裁剪，只保留虹膜外边界内部的部分，设定相应的阈值，同样使用Hough变换确定虹膜内边界圆的位置，如图5所示。

表1 使用5种球面Haar小波基进行虹膜信号重构l 2误差(保留1.56%的小波系数，level=5)

完成虹膜的定位后，需要将虹膜图像中的噪声干扰去除。首先，将图像中虹膜内边界内部区域即瞳孔部分的灰度值置为NaN，去除瞳孔中的亮点。对图像进行二值化，可以将睫毛和瞳孔的区域分离出来，由于之前已经得到了虹膜内外边缘的位置信息，因此以眼睛上睫毛为例，可以将瞳孔以上的虹膜外边界以内的区域选为感兴趣区域，在这个区域中检测睫毛，并确定睫毛的最低点。之后对原图像进行水平方向的Canny边缘检测，对得到的边缘图像使用Hough变换检测直线，即可大致确定眼睑的位置。最后将眼睑的位置与睫毛最低点位置比较，即可确定对虹膜图像上部分的裁剪范围，如图6所示。

使用同样的方法对眼睛的下眼睑和睫毛进行检测，并对虹膜图像进行裁剪。同时，以虹膜外边界内部的区域为感兴趣区域创建掩模，从而去除虹膜外边界周围的噪声干扰。为避免虹膜在图像中的位置不同对虹膜识别造成的影响，将虹膜调整到图像中心，即虹膜外边界圆心与图像中心点重合。最终得到图7所示的虹膜图像。

4.2 特征提取

对输入图像信号进行小波变换。可以证明，当层级j 趋向于无穷时，球面三角形上的函数与该三角形上的尺度函数相同。由于实验中无法将球面无限细分下去，因此将最精细层近似看作无穷层，可以通过将该层球面三角形上的函数值除以尺度函数的归一化常数得到尺度函数系数。

图5 检测得到虹膜内外边缘

图6 检测得到睫毛和上眼睑

图7 分离出的虹膜图像

从最精细一层的球面三角形开始，4个子三角形的尺度函数系数与分解矩阵相乘即可得到父三角形的尺度函数系数以及小波函数系数，以此类推，即可递归求得所有的系数。之后为方便寻找最大的k个系数，将最顶层的尺度函数系数和各层级的小波函数系数按线性索引存储，在系数矩阵中，小波函数系数按层级存储，而每一层级的小波函数系数按其所属的3个不同类型的小波函数分开存储。使用排序算法对系数进行排序，此步骤的计算复杂度为O(NlgN)， 之后选取从大到小排序后的第k 个和第 k+1个 系数的平均值作为阈值，保留前k 个系数，将第 k +1个及以后的所有系数置为0。从而可以 使用最大的k 个系数对原信号进行近似重构。

4.3 虹膜识别

本文使用的虹膜图像来自IITD虹膜数据库和中国东方航空公司的飞行员，包括来自112只眼睛的560张图像，每只眼睛5张图像。随机选取80%的图像作为训练集，20%的图像作为测试集。由于卷积神经网络能够更好地处理高维度数据，本文方法OSSHW的小波系数如前文所述细分层数为7时为131072，传统机器学习方法对于这种规模的数据学习非常困难，而卷积神经网络可以构建更有效的模型进行识别[13]。因此本文使用卷积神经网络来学习OSSHW变换提取的虹膜特征。卷积神经网络结构如图8所示。网络结构包含4个卷积层，使用1维卷积，每个卷积层中的卷积核尺寸均为4、步长为1。每个卷积层后连接BN层和池化层，4个卷积层后连接两个全连接层，神经元个数为1024，使用Dropout来防止过拟合，dropout rate设为0.5。

为验证OSSHW+CNN模型的优越性，与部分传统算法[14,15]以及深度学习算法[16,17]在IITD虹膜数据集上进行对比，实验采用正确分类率(Correct Classification Rate, CCR)作为评价此虹膜识别系统精确度的指标，表示正确分类次数与总分类次数之比。根据表2中数据，使用球谐函数+CNN进行虹膜识别的准确率为91.07%，显著低于使用5种球面Haar小波基时的准确率。其中Bio Haar小波基的识别准确率最低，仅为95.53%。在球面Haar基中，OSSHW小波基+CNN提供的虹膜识别准确率最高，为98.21%, Nielson+CNN提供的准确率为96.42%, Bonneau+CNN和Pseudo Haar+CNN提供的准确率为97.32%。

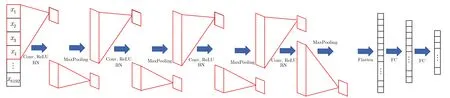
图8 卷积神经网络结构图

表2 使用不同球面信号分析方法的识别准确率

与主流虹膜识别算法相比，OSSHW+CNN模型的虹膜识别准确率高于传统算法以及绝大部分深度学习算法，仅仅略逊于IrisConvDeeper算法。而以IrisConvDeeper算法为代表的深度卷积网络均需构建复杂的深度卷积网络用于虹膜图像特征提取，模型的识别准确率及精细特征提取能力很大程度依赖于网络的深度和复杂度，因此具有参数量大、计算复杂度高、模型训练时间长等缺点。与之相比，本文提出的OSSHW小波基与CNN结合的虹膜识别框架主要使用球面小波基对虹膜精细特征进行提取生成特征向量，因此仅需构建包含4层卷积层的CNN模型即可实现对虹膜的高精度识别，训练时间、参数量以及计算复杂度均远远优于上述各类深度学习模型。考虑到虹膜识别系统运行速度等原因，OSSHW的球面细分层级设为5，使得提取的虹膜特征维度适中，保证了识别速度，但并不能完全保留虹膜纹理信息，从而也导致识别准确率优势不够明显。

5 结论

本文提出一种基于正交对称的球面Harr小波的虹膜识别方法，它能有效地避免平面虹膜图像造成的纹理扭曲现象，提高虹膜识别的准确率。本文的贡献主要归纳如下：

(1)提出一种基于球面Haar小波的使用球面信号来代替平面信号进行虹膜特征学习的方法，它比传统球谐函数以及其他各类球面Haar小波基具有更强的球体表面信息捕获能力。

(2)提出一种正交且对称的球面Haar小波基OSSHW的构建方法，并推导出其尺度基函数和小波基函数。

(3)对比分析了Bio Haar小波基、Nielson小波基、Bonneau小波基和Pseudo Haar小波基对球面虹膜信号进行分解和重构的性能。

(4)提出基于正交且对称的球面Haar小波和CNN的联合学习框架，实现虹膜图像的精确识别，并与主流虹膜识别算法进行比较。实验结果表明，使用具有正交性的球面Haar小波基相对于球谐函数和半正交小波基等各类球面Haar小波基具有更高的准确率。