在线优化参数的变时滞无模型自适应单值预测控制

侯小秋

(黑龙江科技大学 电气与控制工程学院，黑龙江 哈尔滨 150022)

针对复杂非线性系统难以建立被控系统数学模型的控制，侯忠生[1]教授提出了数据驱动控制的无模型自适应控制。笔者在近几年对时变时滞的非线性系统的无模型自适应控制做了一些研究，在文献[2-4]中对侯忠生教授提出的紧格式动态线性化存在的问题进行了分析，提出了具有辅助变量和辅助向量的改进的紧格式动态线性化方法。文献[2-3]中改进的紧格式动态线性化方法可适用于随机干扰和快变化干扰，文献[4]中改进的紧格式动态线性化方法可适用于慢变化干扰。文献[2-4]对在线修正参数的变时滞的无模型自适应PID控制进行了理论和仿真研究，对提出的改进的紧格式动态线性化方法的有效性进行了验证，文献[5]研究了自适应单值预测控制问题，文献[6-8]研究了无模型自适应预测控制问题。在上述研究的基础上，本文研究在线优化加权网络参数的变时滞的无模型单变量系统的自适应单值预测控制。文献[5-8]研究的自适应预测控制的加权网络参数为试凑法取值，无法保证控制算法最优，本文使用非线性递推最小二乘法对其进行在线优化，解决了试凑法确定加权网络参数取值不能使系统最优运行的问题。

1 改进的泛模型及参数估计

1.1 改进的泛模型

根据文献[2,4]的研究结果，当干扰为慢变化干扰和常值干扰，以及噪信比较小的快变化干扰和随机干扰时，给出改进的具有辅助变量的紧格式动态线性化方法的泛模型：

Δy(t)=q-dφ(t)Δu(t)+v(t)，

(1)

式中y(t)为系统输出，u(t)为系统输入，d为时滞，v(t)为辅助变量，φ(t)为偏导数参数，Δ为多项式，且Δ=1-q-1。

该泛模型克服了侯忠生教授提出的泛模型存在的几个问题，详细论述见文献[2,4]。

1.2 参数在线联合估计

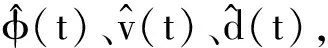
2 无模型单值预测控制

参考文献[5]的单值预测控制算法和文献[6-8]的无模型自适应预测控制，给出如下无模型单值预测控制算法。

由式(1)逐步迭代得到输出预测模型

(2)

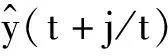
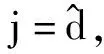
(3)

选取目标函数为

(4)

式中yr(t)为系统参考输入，θ(q-1)为加权网络，且

θ(q-1)=θ0+θ1q-1+…+θmq-m，

(5)

式中m为维数，θi(i=0,1,…,m)为加权网络参数。

把式(3)代入式(4)，并令dJ/du(t)=0，则有

(6)

亦即

(7)

从而得到控制算法：

(8)

式中θ′(q-1)为加权网络，且

θ′(q-1)=θ1+θ2q-1+…+θmq-(m-1)。

(9)

3 加权网络参数在线寻优

3.1 梯度表达式

由式(8)可得控制算法可调参数向量为

ηT=[θ0,θ1,…,θm]，

(10)

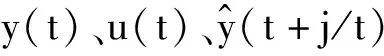
式(1)两边对ηi求偏导得

(11)

由式(11)可得∂y(t)/∂η。

式(2)两边对ηi求偏导可得

(12)

式(8)两边对θ0求偏导可得

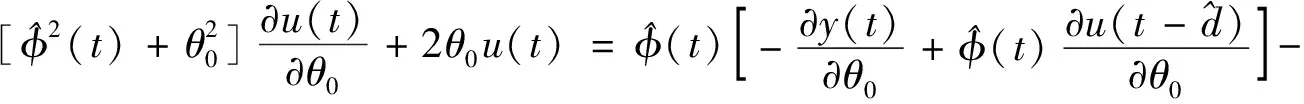
(13)

式(8)两边对θi(i=1,2,…,m)求偏导得

(14)

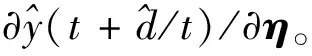
3.2 在线优化加权网络参数算法

将文献[10]中用于辨识的非线性递推最小二乘法经过改进，并应用此处进行加权网络参数寻优。

算法目标函数为

(15)

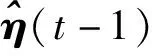
λ(t)=diag[λ1(t),λ2(t),…,λm+1(t)]，

(16)

(17)

将目标函数式(15)改写为

(18)

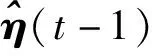
(19)

(20)

将式(19)和(20)代入式(18)可得

(21)

式(21)两边对η求偏导得到

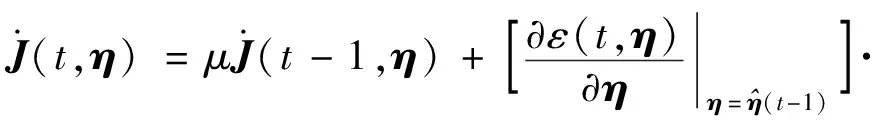
(22)

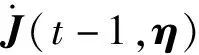
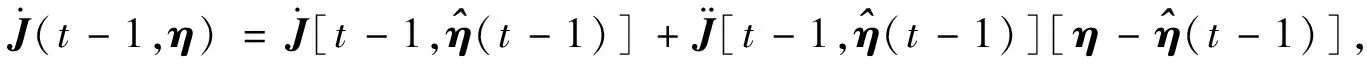
(23)

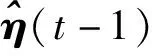
(24)

(25)

式中

(26)

式(22)两边对η求偏导，可得

(27)

则由式(26)和(27)得

(28)

由式(28)可得

(29)

则由式(26)和(29)可得

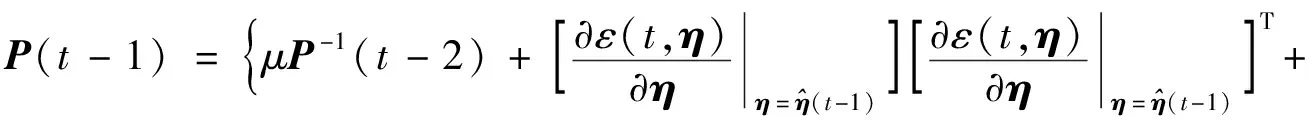
(30)

式中

(31)

式(17)两边对η求偏导可得

(32)

综上分析，由式(25)和(30)可构成加权网络参数的在线优化参数算法。式(30)的矩阵求逆及克服算法病态的λ(t)的确定可应用文献[11]的算法。

4 仿真研究

0≤t≤200时的被控对象模型(d=7)为

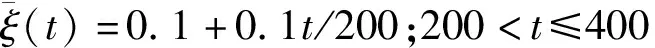
yr(t)=1(t)。

控制输入的饱和限幅为Umax=0.8，目标函数中的加权网络的维数m=2，加权网络参数初始值为

优化算法中的

P(-2)=106I，α=1，μ=0.98，

泛模型待估参数的初始值

采用MATLAB 7.01编制m文件程序实现仿真研究，图1给出系统的无算法参数优化和有算法参数优化的单位阶跃响应曲线。由图1(a)可看出无算法参数优化时的响应曲线有大的超调，在t=200时由于被控对象数学模型的改变，导致系统出现一定超调，由图1(b)的有算法参数优化的单位阶跃响应曲线可以看出，系统响应具有较小的震荡和超调，无稳态偏差，表明给出的泛模型逼近系统的性能优良，验证了给出的泛模型的有效性，同时说明泛模型待估参数的估计合理，加权网络参数的在线优化效果佳。

(a)无优化 (b)有优化

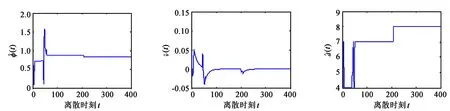
图2给出了加权网络参数的在线优化曲线，可以看出，系统运行处于动态时，算法的加权网络参数进行参数优化，系统运行处于稳态时，系统稳定的运行进入稳态控制目的，算法的加权网络参数合理有效无需优化，遵循算法的物理性质。

5 结论

(1)单变量系统的自适应预测控制与时变时滞无模型自适应预测控制相结合的研究，探讨时变时滞的在线优化加权网络参数的无模型单变量自适应单值预测控制。

(2)使用非线性递推最小二乘法对控制算法的加权网络参数进行在线寻优，克服了试凑法取值不能保证系统最优运行的问题。

(3)基于控制算法和系统泛模型及预测模型，理论推导了控制输入序列和输出及输出预测序列关于加权网络参数的梯度，算式简单，计算量小。

(4)将本文研究机理推广于多变量及偏格式动态线性化及全格式动态线性化，需进一步研究算法的稳定性。