螺杆压缩机转子动态特性研究

李志峰， 晁 瑞， 王智博， 张永涛， 万旭东

(陕西理工大学 机械工程学院，陕西 汉中 723000)

喷油式螺杆压缩机采用阳螺杆转子驱动阴转子运动，在压缩机内有润滑油可起到润滑、冷却和密封等[1-2]作用，但是螺杆转子之间的啮合转动会存在接触力，且接触力的波动对压缩机整体效能影响极大，故对转子间啮合力的研究很有意义。

国内许多学者均采用虚拟样机技术对转子间啮合力进行研究，李海林等[3]利用ADAMS软件模拟螺杆转子工况，对转子的转速进行了验证；吴万荣等[4]利用MATLAB软件仿真系统建立压缩机系统模型，并对其特性进行研究；刘军等[5]以挖掘机回转齿轮为模型，在ADAMS中进行啮合力仿真分析；王亮等[6]建立了采煤机传动系统的模型，对高速级齿轮的啮合力变化进行了分析。综上所述，对压缩机转子工作过程中的振动及啮合特性等研究较少。本文通过设计螺杆转子截形并建立螺杆转子模型，验证是否产生共振，并在ADAMS软件中对啮合力影响因素进行研究。

1 建立虚拟样机

以某型号螺杆压缩机阴、阳螺杆转子为研究对象，设定阴、阳转子求解的初始参数，阳转子节圆直径为74.545 mm，阴转子节圆直径为89.455 mm，传动比i=5 ∶6，中心距为82 mm。根据上述参数利用MATLAB软件求解得到阴、阳转子的齿形如图1所示。

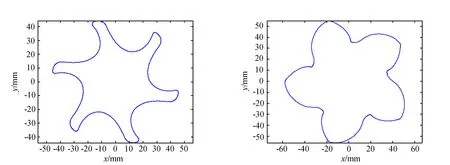
(a)阴转子齿形 (b)阳转子齿形

将MATLAB求解所得阴、阳转子一系列型线点数据在UG软件中进行离散点的拟合，得到端面型线，建立阴、阳转子的装配模型并检查是否存在干涉，同时建立压缩机虚拟样机如图2所示。

图2 螺杆压缩机转子几何模型

2 材料设置

压缩机螺杆转子的材料目前多采用合金结构钢40Cr，其物理参数分别为数值弹性模量E=210 GPa，密度ρ=7850 kg/m3，泊松比μ=0.3。对阴、阳转子上键槽、螺纹和倒角等影响较小因素进行简化，对其进行网格划分，保证其网格无关性。

3 运动学分析

3.1 接触力参数

ADAMS软件中接触力计算方法主要有Restitution-base contact和Impact-Function-base contact，前者主要采用惩罚参数和回归系数计算接触力，后者则是利用软件中IMPACT函数计算接触力，文中采用第二种方法。将做啮合运动的转子视为刚体，忽略阴阳转子之间的弹性振动和齿间间隙的误差，转子之间的碰撞力定义如式：

其中K为两螺杆转子的刚度系数(N/mm)，e为碰撞指数，x为两螺杆转子之间的挤压变形量(mm)，d为两螺杆转子之间的切入深度(mm)，C为最大阻尼系数。

接触力设置主要包括4个参数，即刚度系数K、碰撞指数e、最大阻尼系数C、切入深度d。刚度系数K(两螺杆转子受外载荷发生变形的物理量)计算公式[7-8]如下：

式中R1和R2分别为两转子接触处的径向值，μ1和μ2为两转子的泊松比，E1、E2为两转子的弹性模量。求得刚度系数 为1.036×106N/mm；碰撞指数e表述材料的非线性变化，查询文献[9]金属之间碰撞一般取1.5；最大阻尼系数C表述材料的阻尼属性，一般取0.1%～1%的刚度系数；切入深度d表述两转子碰撞时侵入深度，金属之间碰撞取0.15 mm。查询文献[10]知，金属之间添加润滑油后的接触动摩擦因素为0.05，静摩擦因数为0.08。

设置螺杆压缩机中阳转子某工况转速1500 r/min，因此给阳转子添加驱动角速度为9000(°)/s；如果直接给定恒值，软件仿真中易出错，故调用内部STEP函数设置阳转子角速度：STEP(time，0，0，0.2，-9000 d·time)，表示0～0.2 s内角速度平稳过渡到9000(°)/s后维持不变。在阴转子轴上添加负载转矩：STEP(time，0，0，0.2，-100 000 N·mm)，表示0～0.2 s负载转矩平稳过渡到-100 000 N·mm后维持不变。

3.2 转速验证

将上述参数设置好，设置EndTime为0.2 s，StepSize为0.000 1 s，进行仿真测试。

建立的虚拟样机中阴、阳转子转速0.2 s 内速度如图3所示，根据螺杆转子传动比关系，阴转子角速度应为7500(°)/s，测得阴转子的平均转速-7 536.13(°)/s，误差相差0.48%，符合压缩机工作时的传动比转速要求。

图3 阴、阳转子转速

3.3 阻尼对啮合力的影响

由图4可知，两个螺杆转子开始工作时，有明显的碰撞力波动，但基本保持在均值左右。在转速、刚度、载荷等不发生改变的情况下，选取0.1%、0.5%、0.9%刚度系数进行仿真可知，适当降低阻尼系数可以使接触力幅值大量降低，且使啮合力波动明显减小。

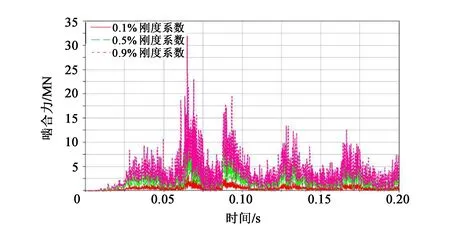
图4 不同阻尼系数下的时域图

以0.1%的刚度系数作为阻尼系数为例，仿真分析后的平均啮合力为5.097×105N；根据Hertz理论可知，两旋转体之间碰撞力计算公式为

其中Fn为法向接触力(N)，K为刚度系数(N/mm)，P为添加在转子上的载荷(N)，ρ为综合曲率半径(mm)，E为综合弹性模量。

理论计算求得螺杆转子的平均啮合力为4.662×105N，与仿真值相比较小，这是由于Hertz理论算法与ADAMS软件中内部Impact算法存在差异，但总体啮合力基本保持一致。

3.4 不同工况下的啮合力变化

分别对工况一到工况五进行运动仿真分析可得到表1中啮合力数据，由工况一到工况三可知在相同转速下，在阴转子上采用Step函数施加不同的负载转矩，可知随着负载转矩的增加，啮合力平均值和波动有一定上升趋势但基本保持不变。由工况三到工况五分析可知，在负载转矩保持不变的情况下，随着阳转子角速度增加，平均啮合力大幅度增加且波动也明显变大。

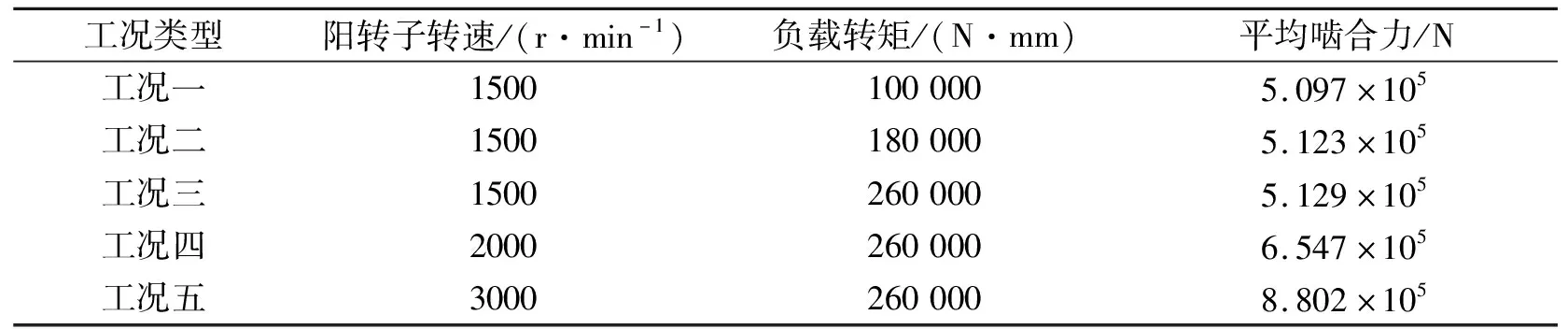
表1 不同工况下啮合力

4 结论

根据坐标变化和齿廓啮合原理，计算求得螺杆转子端面型线，在UG软件中建立了转子三维模型，进行运动学分析得到以下结论：

(1)在ADAMS软件中进行运动仿真可知：螺杆转子之间的转速符合传动比要求，且转子之间啮合力及其波动与阻尼系数、转速成正相关，负载对啮合力幅值影响较小。

(2)综合可知，利用虚拟样机技术对喷油式螺杆压缩机工作情况进行了模拟分析，为转子的寿命估算、优化设计等提供参考理论。