钛/铝层状复合材料界面损伤有限元模拟

陈 丽，樊瑜瑾

(昆明理工大学 机电工程学院, 云南 昆明 650500)

金属层状复合材料与单一金属材料相比具有较好的比强度,良好的导电、导热、耐高温氧化、抗磨损等性能，可广泛应用于汽车、航空航天、厨具用品、机械电子等工业领域[1-4]。由于结合界面性能薄弱，其中层与层之间的断裂是金属层状复合板的主要损伤形式之一，会严重影响材料的使用性能，因此对于界面的断裂行为研究很有必要。

目前，内聚力单元是研究复合材料界面层的有效方法，大量学者运用内聚力单元对复合材料层间损伤行为进行了一系列研究。内聚力模型的概念最初由Barenblatt[5]和Dugdal[6]先后于1959年和1960年提出。朱兆一等[7]基于内聚力模型，研究了纤维增强复合材料层合板胶接结构时的最大承载能力和界面损伤失效行为。田达等[8]基于内聚力模型，对增韧复合材料进行GⅠ断裂韧性模拟，研究界面参数法相刚度、能量释放率参数对复合材料性质的影响。周彬彬等[9]基于内聚力单元对锆-钛-钢复合板的剪切试验进行了有限元模拟，研究了断裂能和内聚力强度对于界面层损伤的影响。已有的对金属层状复合材料研究大多集中在其制备工艺或断裂失效方面[10-13]，而对金属层状复合材料界面方面的研究相比较少。

本文在结合内聚力模型基本原理的基础上，建立金属层状复合材料端部缺口弯曲(end-notch flexure，ENF)试验的有限元模型，对复合金属板的Ⅱ型断裂分层扩展过程进行仿真数值模拟，研究界面参数对弯曲性能的影响。

1 内聚力模型

内聚力模型的本质是描述原子或分子之间的相互作用，内聚力法则的具体表示为界面层张应力与界面相对张开位移的力学关系，张应力-张开位移的本构方程具有双线性、指数形式、梯形等形式，其中双线性本构关系是研究复合材料层间内聚力模型中最常用的一种本构关系，因此本文选用双线性型内聚力模型来开展界面分层破坏模拟研究，双线性内聚力模型本构关系如图1所示。

图1 双线性内聚力模型

其牵引-分离函数关系为

(1)

式中T为纵向剪切应力，δ为剪切位移，τf为剪切断裂的临界应力，δ0为剪切断裂应力对应的剪切分离位移，δf为剪切断裂的最大位移。

当材料的内聚应力小于剪切断裂的临界应力，即位移在δ0之前时，内聚力单元没有产生损伤，界面处于线弹性阶段，刚度K等于线段斜率，即

(2)

当材料的内聚应力等于剪切断裂的临界应力，即位移等于δ0时界面开始损伤，内聚力单元有多种判断初始损伤的准则，包括最大名义应力准则、最大应变准则、二次名义应力准则和二次名义应变准则等，本文用二次名义应力准则Quads来预测界面退化的初始阶段，具体形式为

(3)

式中σn代表的是纯正常模式的名义应力，σt代表的是在第一方向的名义剪应力，σs代表的是第二方向的名义剪应力。Nmax、Smax、Tmax分别为内聚力单元法向和两个切向方向的强度值，当三者平方和大于1时，开始出现损伤，〈〉为Macaulay算子，其表达式为

(4)

此时损伤开始发展，单元刚度开始下降，界面单元处于损伤软化阶段，对于界面损伤演化过程的软化过程，损伤演化类别有基于位移的损伤演化和基于能量的损伤演化两种，本文使用基于能量的线性软化，损伤起始以后应力更新为

(5)

其中

(6)

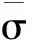
本文采用基于能量释放率的B-K准则作为判断界面最终破坏的失效准则：

(7)

其中Gshare=GⅡ+GⅢ，GT=GⅠ+Gshare，GⅠC、GⅡC、GⅢ为临界能量释放率，η为材料参数。

2 有限元分析模型

本文研究基于文献[14]的试验，采用有限元分析软件ABAQUS建立复合材料Ⅱ型断裂韧性端部缺口弯曲ENF试验的有限元模型，试验中钛/铝复合板由爆炸复合制成，ENF试件几何参数如图2所示，长度为70 mm，铝板厚度为3.5 mm，钛板厚度为2 mm，其中预制裂纹长度为25 mm。

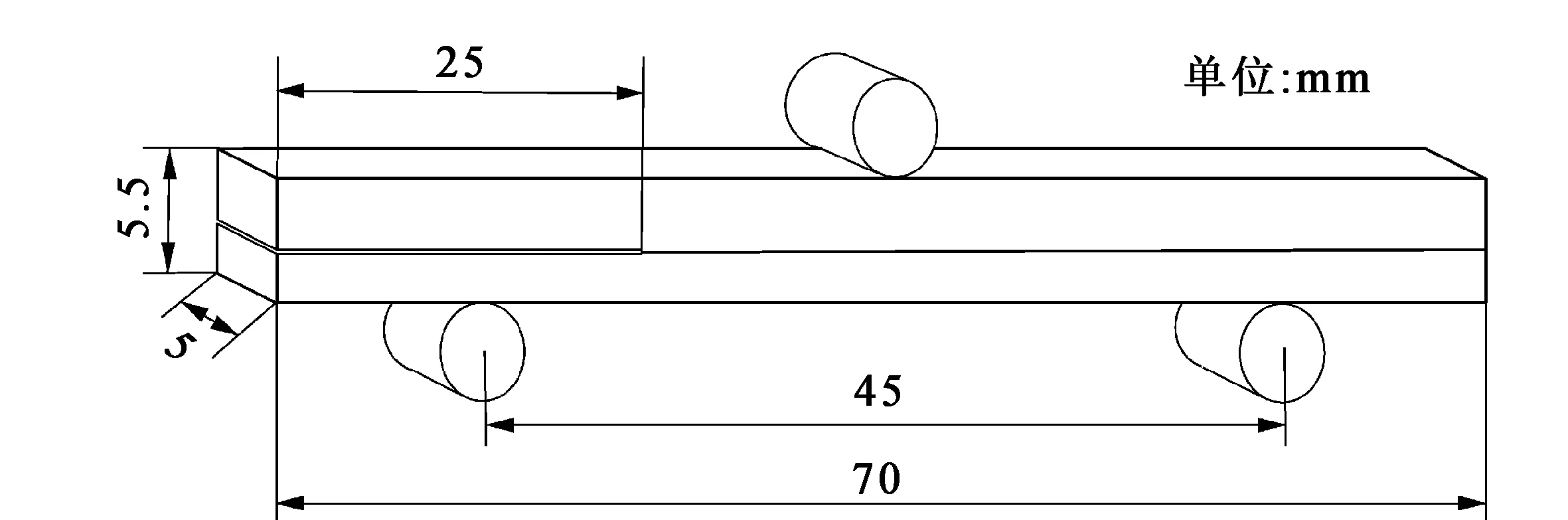
图2 ENF试件几何尺寸示意图

针对金属层状复合材料模型的建立，选择层间特性较好的实体单元建立三维有限元模型，如图3所示。金属板层选用八节点线性六面体单元C3D8R，减缩积分，沙漏控制，界面层采用ABAQUS中的内聚力模型(Cohesive Zone Model，CZM)八节点三维COH3D8粘结单元，厚度值为 0.1 mm。采用扫掠形式自下向上沿厚度方向划分网格。

图3 ENF试件的三维有限元模型

模型施加边界条件，底部两支座3个方向的自由度完全固定约束，加载头与板相切，加载头与点RF1刚度耦合，在RF1 上施加位移载荷-12 mm。支座与加载头和板之间的接触采用基于小滑动摩擦的surface-to-surface contact算法，接触中采用摩擦惩罚因子控制，惩罚因子取为0.2。当内聚力界面单元失效后，层合板的两个子板之间可能会发生穿透。因此，界面之间也需要设置罚刚度接触条件，避免发生穿透。

金属层在ENF试验中发生了弹塑性变形，本文采用幂指数强化模型σ=kεn来定义材料应力、应变关系[15]，界面层为各向同性，材料力学性能参数参考文献[14]，具体如表1、表2所示。

表1 金属层力学性能参数

表2 界面层力学性能参数

3 结果与分析

3.1 模型验证

有限元模拟结果如图4所示。为了验证有限元模拟结果的可靠性，将模拟结果与文献[14]的试验数据进行对比分析并绘制成载荷-位移曲线，如图5所示。由图可知本文仿真的峰值载荷为1 194.8 N，对应位移为9.5 mm，而文献中的峰值载荷为1120 N，对应位移为10.9 mm，则有限元分析结果的相对误差分别为6.7%和12.8%。通过有限元模拟结果与文献试验结果的对比，验证了本文模型的合理性和有效性。

图4 有限元模拟结果

图5 模拟结果与文献[14]结果对比 图6 不同界面刚度对应的载荷-位移曲线

3.2 界面参数对材料性能的影响

为了研究层间材料性能对复合材料数值模拟结果的影响，改变层间材料的界面初始刚度、Ⅱ型能量释放率和剪切强度值的大小，分析其对计算结果的影响。

改变内聚力单元界面初始刚度K的值，选取K为1×104、1×105、5×105MPa/mm的3种情况进行分析，结果如图6所示。由图可知，3种不同界面初始刚度的曲线基本上一致，峰值载荷及其相对应的位移变化在8%左右，说明界面刚度的取值对载荷-位移曲线影响较小。

改变Ⅱ型能量释放率的值，选取GⅡC为13.792、23.792、33.792 N/mm的3种情况进行分析，结果如图7所示。由图可知，在线弹性部分，3种不同能量释放率的曲线基本上重合，峰值载荷对于能量释放率的变化是敏感的，随着能量释放率的增大，峰值载荷值越大，其对应的位移也越大，非线性阶段下降趋势一致。

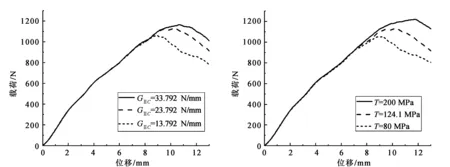
图7 不同能量释放率对应的载荷-位移曲线 图8 不同剪切强度对应的载荷-位移曲线

改变界面切向粘聚强度T的值，选取T为80、124.1、200 MPa的3种情况进行分析，结果如图8所示。由图可知，在线弹性阶段，3条曲线部分重合，剪切强度的变化对于峰值载荷及其对应的位移影响较大，界面剪切强度越大，曲线越高，峰值载荷越大，非线性变化趋势各异。

4 结论

(1)通过有限元软件ABAQUS建立了基于内聚力模型的金属层板ENF弯曲有限元模型，仿真得到了金属层板Ⅱ型层间裂纹扩展的载荷-位移曲线，通过与试验曲线对比，验证了有限元模型的有效性。

(2)界面参数对于金属层板的界面性能有一定影响，其中界面刚度对于性能的影响最小，能量释放率和剪切强度对其影响较大。峰值载荷随能量释放率的增大而相应增大，剪切强度会影响弹性上升段的斜率和峰值载荷，当剪切强度越大时，载荷位移曲线的斜率越大，峰值也越大。