水泥返高对深水高温高压井井口抬升高度的影响

郑双进 程霖 谢仁军 黄志强 武治强 钱肖峰

1. 长江大学石油工程学院；2. 中海油研究总院有限责任公司

在深水高温高压井开发过程中，由于地层高温流体对井筒内油套管以及环空密闭空间流体加热，致使井口抬升，容易导致井口螺栓失效、井口管线损坏等安全问题［1］，如墨西哥湾Marlin油田A-2井由于生产过程中的环空压力过高导致投产数小时后套管和油管破裂变形［2］，南海某气井由于温度效应导致采油树法兰拉脱从而造成天然气泄漏等事故。因此，开展水泥返高对深水高温高压井井口抬升的影响研究十分重要。早在1986年，Klementich、Aasen、McSpadden等人就通过对完井及生产阶段套管载荷分析，建立了单管柱和多管柱井口抬升高度预测模型［3-5］；Liang研究了通过优化水泥返深来控制井口抬升的方法［6］；国内李军［7］、林元华［8］、张智［9］、王宴滨［10］、卢亚锋［11］、董铁军［12］、徐刚［13］、龚宁［14］、张琦［15］、何轶果［16］、熊浩［1］、朱达江［2］、石小磊［17］等人考虑温差效应产生的热应力、环空热膨胀压力等因素建立了井口抬升高度预测模型，预测手段主要为理论数值计算、WellCat软件计算和有限元分析。调研发现，目前关于井口抬升预测方面的理论模型未考虑水泥环胶结强度的束缚影响，且未见水泥环胶结条件下开展井口抬升模拟实验的相关报道。

笔者考虑水泥环胶结强度影响，建立了井口抬升高度计算模型，基于自主研制的高温高压井口抬升模拟实验装置，开展了双层管柱不同水泥返高及多层管柱耦合且固井条件下的井口抬升模拟实验，得到了水泥石胶结对管柱伸长量的影响规律。分析表明本文建立的井口抬升计算模型可用于描述深水高温高压井井口抬升问题，为现场预测井口抬升高度和优化水泥返高提供技术参考。

1 井口抬升计算模型

1.1 单层套管井口抬升预测方法

假设深水高温高压井生产时自由段套管某段的温度由T0i(H)升高至Ti(H)，温度效应所致的单层套管轴向抬升量计算公式［18］为

式中，ΔLi为温度场引起的单层套管轴向抬升量，m；Li为第i层套管自由段长度，m；αc为套管钢材线膨胀系数，一般可取12.1×10-6；Ti(H)为第i层套管在H处生产过程中的温度，℃；T0i(H)为第i层套管在H处的初始温度，℃。

1.2 多层套管井口抬升预测方法

井口抬升高度受温度变化、自由段套管质量、油压、套压、包括井口装置在内的其他设备及固井段水泥环胶结等因素的影响。针对多层套管组成的井口，假设油气井生产一定时间后各层套管自由段长度不再增加，各层套管在井口连接在一起组成多管柱耦合系统，其受力分析如图1所示。

图1 多管柱系统受力分析图Fig. 1 Stress analysis diagram of multi-string system

多管柱系统刚度Kz=ΣKi。各层套管自由段的刚度Ki为［17］

温度变化导致井口抬升高度ΔLt为

其中

自由段套管重力导致井口抬升的高度ΔLm为

油压和套压导致井口抬升的高度ΔLe为

包括井口装置在内的其他设备导致井口抬升高度ΔLw为

固井段水泥环胶结导致井口抬升高度ΔLc为

则井口装置的抬升高度为

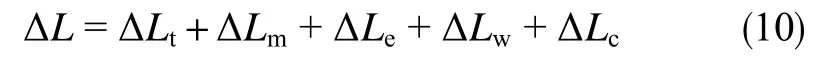
式中，Ki为第i层套管刚度，N/m；Ei为第i层套管的弹性模量，Pa；Ai为第i层套管壁横截面积，m2；εi为第i层套管热应变，无因次；αi为第i层套管线性热膨胀系数，℃-1；ΔTi,j为第i层套管第j段的温度变化值，℃；Li,j为第i层套管第j段的分段长度，m；Ft为多管柱系统受约束而产生的热载荷，N；qi为第i层套管的线重，N/m；rti为油管内径，m；rto为油管外径，m；rc为套管外径，m；pt为油压，Pa；pc为套压，Pa；Wh为井口装置等设备的重力，N；Pn为水泥环内界面胶结强度，Pa；Sn为水泥环内界面胶结面积，m2；Pw为水泥环外界面胶结强度，Pa；Sw为水泥环外界面胶结面积，m2。

人力资源管理信息系统是伴随着人力资源管理发展到一定阶段所产生的，它的出现代表着人力资源管理工作达到了一个更高的层次，这对人力资源管理从业者提出了更高的要求。因此，公司不仅要加强现代人力资源管理理论培训，还要加强信息技术培训，提升人力资源管理从业者信息技术应用水平，打造复合型人力资源管理团队，从而推动人力资源管理信息化建设，并以此为契机，推动企业整体信息化水平的提升。

2 井口抬升模拟实验

2.1 高温高压井井口抬升模拟实验装置

基于实验需求设计了一套高温高压井井口抬升模拟实验装置，如图2所示。本装置运用Ø244.5 mm-Ø177.8 mm-Ø114.3 mm-Ø73 mm管柱模拟构成A、B、C环空，其中Ø73 mm管柱长4.0 m，Ø114.3 mm管柱长3.5 m，Ø177.8 mm管柱长3.0 m，Ø244.5 mm管柱长2.5 m。Ø73 mm管内注满导热油，A、B、C环空均注入有不同密度的盐水以模拟环空保护液。装置底部和顶部均焊接为一体，并保证装置的整体强度、刚度和密封性。Ø73 mm管内加热棒长度为2.5 m，加热功率4 kW，控温精度±1.0 ℃，管柱伸长测量精度0.001 mm。

本文重点研究水泥返高对深水高温高压井井口抬升高度的影响，依托上述实验装置开展了水泥返高50%及100%条件下的双层管柱伸长模拟实验，以及多层管柱耦合且固井条件下的井口抬升模拟实验，对比笔者开展的多层管柱自由伸长模拟实验以及多层管柱耦合不固井条件下的井口抬升模拟实验［18-19］，获得了固井水泥胶结对井口抬升高度的影响规律。

图2 深水高温高压井井口抬升模拟实验装置结构示意图Fig. 2 Schematic structure of simulation experimental device of wellhead uplift of deepwater high temperature and high pressure well

2.2 水泥返高50%条件下的双层管柱伸长模拟实验

Ø73 mm管柱和Ø114.3 mm管柱构成双层管柱环空，水泥浆充填50%，水泥面以上充满密度1.03 g/cm3的盐水，Ø73 mm管内充满导热油，测量45～150 ℃条件下的管柱伸长量，温度每升高20 ℃测试一次。实验模型如图3所示，管柱伸长量实验数据见表1。

图3 双层管柱水泥浆返高50%实验模型Fig. 3 Experimental model of double-layer string with 50%cement top

从表1可看出，管柱伸长量随温度升高而变大，Ø73 mm管柱伸长量增长高于Ø114.3 mm管柱。Ø73 mm管柱管内温度上升较快，150 ℃稳定1.5 h后的伸长量为4.797 mm；依托该实验装置测试套管自由伸长状态下的Ø73 mm管柱井口抬升高度为5.246 mm［19］，本实验相比自由伸长状态下的井口抬升高度降低了约20%(0.449 mm)。Ø114.3 mm管柱由于受水泥石传热的影响，温度上升较慢，伸长量较小，150 ℃稳定1.5 h后的伸长量为3.871 mm；依托该实验装置测试套管自由伸长状态下的Ø114.3 mm管柱井口抬升高度为4.123 mm［19］，本实验相比自由伸长状态下的井口抬升高度降低了约

22.4%(0.252 mm)。

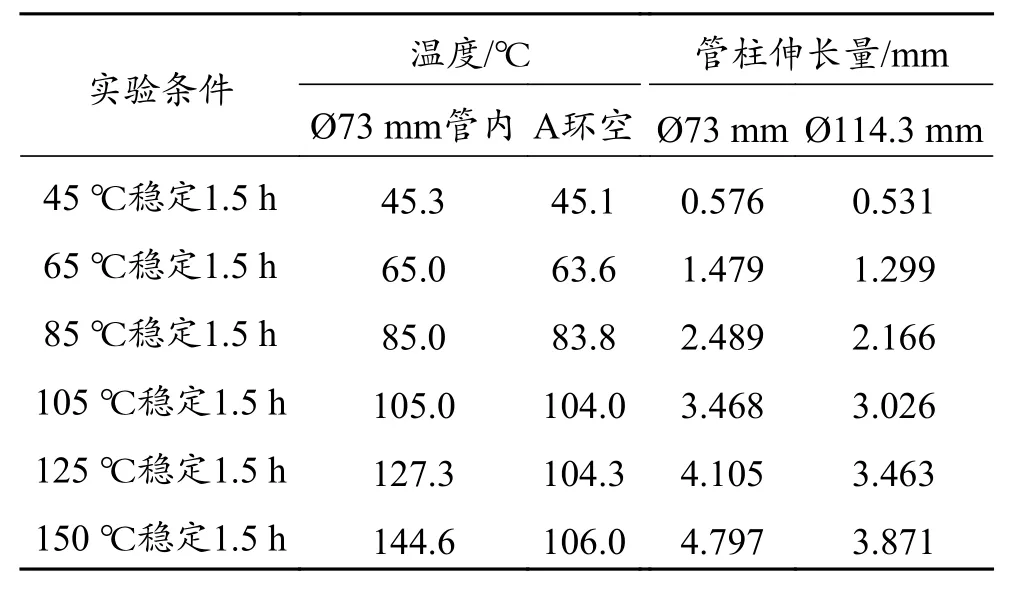
表1 水泥返高50%条件下的双层管柱伸长模拟实验数据Table 1 Simulation experimental data of double-layer string elongation under the condition with 50% cement top

2.3 水泥返高100%条件下的双层管柱伸长模拟实验

Ø73 mm管柱和Ø114.3 mm管柱构成双层管柱环空，环空水泥浆充填100%，Ø73 mm管内充满导热油，测量45～150 ℃条件下的管柱伸长量，温度每升高20 ℃测试一次。实验模型如图4所示，管柱伸长量实验数据见表2。

图4 双层管柱水泥浆返高50%实验模型Fig. 4 Experimental model of double-layer string with 50%cement top

表2 水泥返高100%条件下的双层管柱伸长模拟实验数据Table 2 Simulation experimental data of double-layer string elongation under the condition with 100% cement top

2.4 多层管柱耦合且固井条件下的井口抬升模拟实验

相比多层管柱耦合不固井条件下的井口抬升模拟实验［19］，本实验模型在Ø177.8 mm管柱外增加了一层Ø244.5 mm管柱。A环空充满密度1.03 g/cm3的盐水后封闭，B环空水泥返深50%，水泥面以上环空充满密度1.30 g/cm3的盐水后封闭，C环空水泥返深100%，Ø73 mm管内充满导热油，测量45～150 ℃条件下的管柱伸长量，温度每升高20 ℃测试一次。实验模型如图5所示，管柱伸长量实验数据见表3。

从表3可看出，在多层管柱耦合固井条件下，由于B环空和C环空部分管柱受到了水泥环的胶结作用，整体伸长量都受到了影响。Ø73 mm管柱150 ℃稳定1.5 h后的伸长量为4.280 mm，相比笔者在多层管柱耦合不固井条件下测试的Ø73 mm管柱伸长量5.143 mm［19］，降低了16.8%；Ø177.8 mm管柱150 ℃稳定1.5 h后的伸长量为2.572 mm，相比不固井条件下测试的Ø177.8 mm管柱伸长量4.044 mm［19］，降低了36.4%；Ø114.3 mm管柱150 ℃稳定1.5 h后的伸长量为2.867 mm，相比不固井条件下测试的Ø114.3 mm管柱伸长量4.558 mm［19］，降低了37.0%。

图5 多层管柱耦合固井条件下的井口抬升模拟实验模型Fig. 5 Simulation experimental model of wellhead uplift under the condition of multi-layer string coupling cementing

3 模拟实验与模型计算结果对比

基于笔者开展的多层管柱自由伸长模拟实验发现，管柱的线膨胀系数在(10～20) ×10-6/℃之间［19］，结合实测线膨胀系数，运用1.2部分所建立的井口抬升量计算模型，针对图5所示的实验模型和实验方案开展了井口抬升量计算，计算模型考虑多层管柱耦合受热应力、圈闭压力和水泥环胶结对管柱伸长的影响，此外采用相同的水泥浆体系配方开展了水泥环胶结强度测试，胶结强度平均值为2.35 MPa。管柱伸长量计算数据与模拟实验数据对比见图6。相比实验数据，基于模型计算的管柱伸长量平均误差6.05%，可以满足工程计算需要。

表3 多层管柱耦合固井条件下的井口抬升模拟实验数据Table 3 Simulation experimental data of wellhead uplift under the condition of multi-layer string coupling cementing

图6 多层管柱耦合固井条件下井口抬升量计算与实验数据对比Fig. 6 Comparison between calculated wellhead uplift and experimental data under the condition of multi-layer string coupling cementing

4 结论

(1)固井水泥环的胶结能力对管柱伸长具有不可忽视的影响，相比水泥返高50%工况，双层管柱水泥返高100%条件下管柱伸长量明显降低，相比多层管柱耦合非固井工况，固井条件下的井口抬升模拟实验管柱最大伸长量可降低36.5%左右。

(2)本文所建立的井口抬升计算模型与模拟实验相比误差小于10%，可用于预测实际井口抬升高度。为了降低井口抬升高度，采用低线膨胀系数管材，适当增加水泥返高以及提高水泥环胶结强度有助于降低井口抬升高度，促进深水高温高压井井口完整性。