基于模型试验的再生混凝土骨料包裹桩承载力计算理论研究

何 旭，王志佳，李胜民，段书苏，梁 平

(1 海南大学 土木建筑工程学院，海南 海口 570228；2. 广州华科工程技术有限公司，广东 广州 511450)

随着城市建设的可持续发展，大批量建筑垃圾的处理问题已成为学术界研究的焦点[1].建筑垃圾中的可再生混凝土骨料具有良好的透水性且拥有较高强度，Sachdeva[2]等在传统建筑垃圾处理的基础上将其作为颗粒桩材料用于地基处理.目前，颗粒桩技术在地基处理中已得到广泛的应用，已有研究表明：颗粒桩在处理地基中因土体提供的约束不足时易发生鼓胀破坏[1,3].为解决此问题，工程上采用土工材料对颗粒桩进行包裹为桩体提供附加约束，其中以包裹碎石桩技术最为常用.考虑到碎石是混凝土的基本原料，为节约工程建设成本，采用建筑垃圾中的再生混凝土骨料替换包裹碎石桩中的碎石，形成一种再生混凝土骨料包裹桩.

现有包裹颗粒桩承载特性的研究方法多围绕模型试验和有限元分析，为更好的满足包裹桩的工程应用，有关包裹颗粒桩承载特性的理论研究也非常有必要.基于此，Raithel[4]等基于碎石桩单元体首次提出了单元理论计算模型.Alexiew[5]在工程中利用该模型研究了土工材料对桩体承载和沉降的影响.发展至今，用于包裹桩承载力的计算方法主要包含：带有重要简化假设的近似计算法和基于复杂建模的有限元法[6].

带有重要简化假设的近似计算法以Brauns法为代表，假设包裹桩加固地基的受荷载区域无限，且桩径和桩间距不变桩和土体处于轴对称态，在未包裹桩体基础上考虑包裹材料的约束.因此，诸多学者对该方法展开了进一步的研究：杨有海[7]在Brauns法的基础上以加固土体的强度为基础，提出包裹桩承载力计算公式.Tandel[8]、赵明华[9]、Murugesan[10]、欧阳芳[11]和Ayadat[12]等以桩体鼓胀破坏为基础，采用极限平衡理论对桩体承载力展开了计算.赵明华[13]以Brauns法为基础，综合考虑包裹材料、土体约束及桩土接触面剪切力的影响，采用弹塑性理论推导了桩体承载力的计算方法.但以Brauns法为基础进行桩体承载力计算时，多以桩体计算深度处的竖向应力展开桩顶荷载预测，计算结果存在较大误差，偶然性较大.

采用基于复杂建模的有限元分析法进行桩体承载力计算时，所考虑的影响因素较多，计算模型与桩体实际受力较为接近，其计算结果较带有重要假设的简化算法更为精确.目前，部分关于包裹桩应力及变形研究均采用此方法进行，Wu[14]根据桩体体积应变和轴向应变的归一化关系，采用圆孔扩张理论研究了包裹桩的应力-应变关系，并探讨了各设计参数对桩体承载力的影响.Pulko[6]在考虑包裹桩的竖向应力分布及桩体鼓胀变形后，结合颗粒桩与刚性桩的计算方法提出了包裹桩在不同设计参数下的封闭解.Wu[15]在已有研究的基础上，由桩侧变形速率与偏应变的关系，建立了围压增量和套筒鼓胀的偏应力计算公式，同时对桩体承载性能展开了分析.Zhang[16-17]以包裹碎石桩的轴对称单元模型为基础，给出了桩体承载力及变形的精确弹性解.Lo[18]等人以单元模型为基础，结合数值研究给出了桩体沉降的完全耦合解.Duan[19]假定包裹桩破坏时土体和包裹材料保持弹性状态，推导了桩体承载力的弹塑性解.结合以上研究成果可知：基于复杂建模的有限元法计算过程繁琐，且不同文献所采用的计算方法均围绕各自的重点展开，缺乏统一的标准.因此，提出一种简单合理的包裹桩承载力设计计算方法非常有必要.

综上所述，已存包裹颗粒桩的理论算法多集中于包裹碎石桩，考虑到碎石与再生混凝土骨料的差异性，有关包裹碎石桩的理论算法已不能直接应用于再生混凝土骨料包裹桩.为更好地满足再生混凝土骨料包裹桩在工程中的应用，笔者对其承载力的计算理论展开研究，提出一种既适用于包裹碎石桩又适用于再生混凝土骨料包裹桩的承载力计算方法.理论推导过程中以模型试验结果为基础，在考虑桩土自重的基础上采用极限平衡理论和弹塑性理论，对以鼓胀破坏为主的再生混凝土骨料包裹桩在不同刚度和桩径下桩体承载力的计算方法展开研究，并基于试验结果对计算公式进行修正，以期为再生混凝土骨料包裹桩的工程应用提供设计计算方法.

1 单桩承载力试验研究

1.1 试验设计以全长包裹的再生混凝土骨料桩为例，对不同包裹刚度和桩径的桩体承载力展开研究，通过变化包裹材料层数以改变包裹刚度.试验相似比λ(λ为原型与模型桩径的比值)为10，模型桩长700 mm，桩径100 mm，长径比为7 ∶1.模型箱尺寸根据模型桩的影响区域大小进行确定，以避免模型箱边界对土体产生影响.已有研究指出包裹颗粒桩的影响区域大小为2～4倍桩径[20]，基于试验模型的最大桩径d为115 mm，最终确定模型箱尺寸为600 mm(长)×600 mm(宽)×900 mm(高)，模型箱材质为OSB板.试验共设计9组，分组详情如表1所示，其中1～6组研究包裹刚度的影响，1、2、7～9组研究不同桩径的影响.

表1 试验分组

为研究桩体的变形，采用6个型号为KSKS16-500-V10的拉线位移计对试验过程中桩身的变形进行监测.为保证桩身径向鼓胀变形值可有效传递至拉线位移计，单独设计了由拉线位移计、PVC管和软塑管共同组成的变形监测装置，PVC管和软塑管为拉线提供通道，减少拉线与土体接触产生的摩擦.模型施工时所有位移计均采用木支架固定于模型箱的边缘.拉线位移计安装过程中需对拉线进行预拉20 mm的位移量，避免桩体因拉线松弛无法监测到变形值，拉线位移计及布置如图1所示.

1.2 试验材料试验用的再生混凝土骨料由强度为C30的废弃混凝土块加工而成，最大粒径10 mm.试验土层由下部坚硬层和上部砂土组成，砂土取自海南省当地具有液化特性的海砂，最大粒径5 mm，由土工试验测得再生混凝土骨料和砂土的物理参数如表2所示，级配曲线如图2所示.根据统一土体分类标准，再生混凝土骨料和砂土分别归类为SP和GP.由级配曲线测得混凝土骨料和砂土的不均匀系数Cu分别为4.28和2.44，曲率系数Cc分别为2.51和1.09.坚硬层由粒径为5～10 mm的碎石组成，层厚100 mm.

表2 砂土和再生混凝土骨料参数

Mehrannia[21]等研究表明：包裹颗粒桩的实际工程应用中，土工材料的刚度采用范围为50～2 000 kN·m-1，土工格栅刚度一般低于4 000 kN·m-1.选择的包裹材料为尼龙质土工材料，并通过变化包裹的层数改变桩体的包裹强度.经万能试验机分别对1～4层的带缝制缝和未有缝制缝的试样展开宽幅拉伸试验[22]，拉伸试验结果如图3所示.取延伸率5%对应曲线的割线斜率为材料刚度，测得所选土工材料的最大刚度为145 kN·m-1.包裹材料采用Buckingham π[23]相似定理进行设计，其结果如表3所示.以相似设计反推原型包裹材料刚度为1 450 kN·m-1，满足工程要求.试验取带缝试样的测试参数为试验的设计指标，相关物理指标如表4所示.

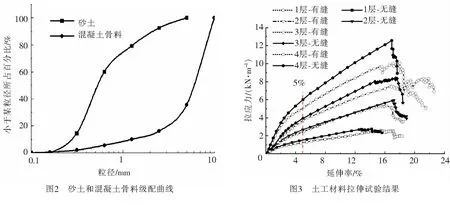
表3 土工材料相似比设计

表4 包裹材料拉伸强度指标

1.3 模型制作及加载试验模型土体包含2层，下层为粒径小于10 mm的碎石颗粒组成的坚硬层，坚硬层分2层施工并进行击实，每层厚50 mm.坚硬层施工完成后在其上放置2层土工材料，以阻止上层土体与坚硬层发生混合.上部土层为砂土层厚700 mm，砂土的填筑和桩体的施工同步分层进行，砂土每层压实后的层厚为100 mm.为确保每层砂土的密实度接近，施工前称重60 kg的砂土放入模型箱中压实使每层的填筑密度达到1 664.1 kg·m-3.

施工再生混凝土骨料包裹桩时，在模型箱中心固定一根长300 mm，内径与桩径一致的PVC套管，套管为桩体提供附加约束，防止桩体压实时混凝土骨料挤破包裹套筒并确保桩体的垂直度.PVC套管固定完成后，向套筒内放入土工套筒开始分层填筑混凝土骨料，为保证混凝土骨料达到1 387.3 kg·m-3的填筑密度，每层称重0.6 kg的混凝土颗粒放入包裹套筒内并击实.桩体击实采用采用直径20 mm，长1 000 mm的振捣棒进行，每层击实20次，每次从200 mm的高度自由落下，以确保每层混凝土骨料的相对密度相当.无包裹桩的施工直接在PVC套管内进行，其施工方法与再生混凝土骨料包裹桩相同.

桩体和砂土的同步施工过程中，每施工2层桩体后填筑一层砂土，桩体先于砂土施工并保持100 mm的高度差，成桩套管在桩体击实过程中缓慢提升，并始终与桩体保持50 mm的接触高度.当模型施工到桩体变形监测位置时安装拉线位移计，拉线位移计安装完成后重复上一阶段的施工直至模型施工完成.模型加载采用位移控制的等速率贯入法进行，位移速率1 mm·min-1.桩顶沉降量达到50 mm时试验结束(桩长的7%)[10].

1.4 试验结果试验通过变化包裹材料的层数以改变桩体的包裹强度，并采用了1～4的土工包裹材料对桩体进行包裹以探究包裹刚度对桩体承载性能的影响.拥有不同包裹刚度的桩体荷载沉降曲线(F-S)如图4所示.

由图4可知，增加包裹刚度能显著提高桩体极限荷载，当桩顶沉降值为50 mm时，对应极限荷载由无包裹桩体的2.6 kN提高到4层包裹的4.8 kN，提高近1倍，极限荷载随包裹刚度的增加而增大.当桩顶荷载F小于2 kN时，4种不同刚度包裹桩体的荷载沉降曲线几乎重合，此时包裹刚度的优势并未得到充分发挥；桩顶荷载大于2 kN后，曲线的斜率随着包裹刚度的增加而减小，不同刚度的包裹材料提供的约束性能开始发挥，当包裹刚度增加到102.2 kN·m-1时，荷载沉降曲线已接近为一条具有弹性材料性能的直线.

考虑到再生混凝土骨料为力学性能已受过损伤的材料，其强度较传统的碎石颗粒低.为研究再生混凝土骨料包裹桩在承载过程中混凝土骨料是否发生破碎，试验结束后取桩顶至200 mm桩体深度内的骨料展开级配分析，以探究桩顶荷载作用下骨料颗粒的破碎情况并采用Hardin[24]模型对颗粒的破碎大小进行度量.拥有不同包裹刚度的桩体极限荷载和芯料的破碎如表5所示.

表5 拥有不同包裹刚度的试验结果

由表5可知，桩体的极限荷载和破碎率随包裹刚度的增加增大.为了进一步研究包裹刚度对桩体极限荷载的影响规律，对表5中桩体极限荷载与包裹刚度之间的变化规律进行拟合，拟合结果如图5所示.

由图5可知，图中桩体极限荷载增长速率随包裹刚度的增加逐渐减小，通过图中拟合公式可得：当包裹材料刚度为100 kN·m-1左右时，桩所能承受的极限荷载达到最大值4.67 kN，大于该值后增一步增加包裹材料刚度桩体极限荷载不再发生变化.

为探究再生混凝土骨料包裹桩承载力与芯料破碎率的变化规律，现对再生混凝土骨料展开了侧限压缩试验，研究了不同粒径下的骨料破碎情况，图6为各粒径的再生混凝土骨料的相对破碎率随竖向荷载的变化曲线.

由图6可知，在试验过程中粒径5.00～10.00 mm试样的骨料破碎度明显高于其他粒径的试样.当竖向荷载小于10 kN时，颗粒的破碎度与竖向荷载几乎呈线性关系变化且粒径小于5.00 mm和自然级配的试样颗粒破碎值较为接近.竖向荷载在10～14 kN时所有曲线出现平台区，荷载大于14 kN时颗粒的破碎度显著增加.因此，将再生混凝土骨料作为颗粒桩材料用于地基处理时，在桩体施工和承载过程中应确保荷载小于14 kN并保证再生骨料的良好级配，以避免再生混凝土骨料因荷载过大产生过度的颗粒破碎.本文试验的最大荷载值为4.8 kN且相对破碎率小于0.2，可认为再生混凝土骨料只发生轻微的破碎，桩体可有效承担桩顶的荷载.

探究桩径影响时，试验采用了表1所示的4种桩径的全长包裹桩体进行试验，4种桩体的桩长为700 mm，均采用1层土工材料进行包裹.4种桩径的桩体荷载沉降曲线如图7所示.

由图7可知,桩顶沉降为50 mm时，桩顶极限荷载由桩径为56 mm的2.57 kN增加到桩径为115 mm的3.95 kN，总体承载能力提升54.3%.因此，增加桩体的桩径可有效提高再生混凝土骨料包裹桩的承载能力.桩径为56 mm和70 mm对应桩体的极限荷载值较为接近，桩径对桩体承载特性的影响不明显，4种桩径的桩体极限荷载如表6所示.

表6 不同桩径的桩体极限荷

为研究桩顶荷载作用下不同试验工况对应桩体的变形特性，沿桩身布置6只拉线位移计，用于监测桩身径向变形沿桩长的分布规律，最终规律如图8所示.

图8中径向变形率为所测变形量与原桩体周长的比值.由图8a可知,当桩体深度小于4倍桩径深度时，桩身径向变形率随着包裹刚度的增加而减小，在桩体4倍桩径以下深度内，包裹材料刚度大于49 kN·m-1时，增大包裹刚度对桩体的变形约束不明显.桩体的主要鼓胀变形区发生于桩顶至5倍桩径深度内，最大鼓胀变形位置位于桩顶.在5倍桩径深度以下区域无包裹桩体的鼓胀变形率接近0，而包裹桩在该区域发生了微小变形，变形率约为5%.由图8b可知，桩长保持不变时，随着桩径的减小径向变形率减小，而桩径为56 mm的桩体，桩身的变形波动较大.

2 单桩承载力理论研究

2.1 基本假定为简化再生混凝土骨料包裹桩单桩承载力计算，现做如下假设：

1) 再生混凝土骨料包裹桩承载过程中，桩体发生鼓胀破坏且混凝土骨料不发生破碎，土体与桩体的破坏满足摩尔库伦准则.

2) 在桩体计算区段的任意深度处，桩体和土体接触面处于极限平衡状态，再生混凝土骨料桩、包裹材料和土体满足变形协调条件.

3) 土工材料为线弹性材料，桩体发生鼓胀破坏时包裹材料处于线弹性状态且达到极限抗拉强度.

2.2 不同包裹刚度的桩体承载力研究无包裹再生混凝土骨料桩的承载力来源于桩周土体的侧向约束.因此，合理的展开桩周土体的约束力计算对桩体承载力的评价至关重要.已有文献[3,8,20,25-26]提出无包裹颗粒桩桩顶竖向承载力可采用式(1)展开计算.

σv=tan2(45°+φc/2)·σh,

(1)

σh=K0(q+γs·z0)+k·cs,

(2)

其中，φc为颗粒材料内摩擦角，K0为静止土压力系数，q为作用于土体表面的荷载，γs为土体重度，z0为计算深度，cs土体粘聚力，k为常数.

Kong[27]研究指出,土体提供的约束力σh处于静止土压力与被动土压力之间.文献[1,3,8,10,25-26]进行土体约束力σh计算时均采用静止土压力理论，使得(1)式得到的计算结果小于实际值，且该式多以计算深度所在点的竖向应力表观桩顶应力，其计算结果存在较大误差.现有文献研究发现：包裹桩主要鼓胀变形区段为于桩顶至5倍桩径深度范围内[3,10,25].结合本文试验结果，现取5倍桩径的桩体长度作为计算长度，并以该区段土体的总约束力对桩体承载力展开计算，计算示意图如图9a所示.

考虑到土体的约束力由桩体鼓胀变形诱导产生，故土体的约束力σhs采用被动土压力理论展开计算

σhs=tan2(45°+φc/2)·(γsz0+q)+2cstan(45°+φc/2),

(3)

其中，φs为土体内摩擦角.此时，桩顶竖向应力σv可通过对式(3)进行计算深度上的积分得到

(4)

(5)

土工材料的约束力σgeo，由土工材料宽幅拉伸试验所测极限抗拉强度Tmax和试验桩桩径r展开计算.计算模型如图9b所示，包裹材料提供约束力σgeo在y向的受力满足

(6)

由式(6)可得包裹材料的约束应力σgeo满足

(7)

联立式(4)～(7)展开桩体承载力计算，所得结果如表7所示.

表7 桩体承载力计算结果

α=0.000 001A2-0.001 9A+1.85，

(8)

(9)

采用式(9)修正后的承载力计算值如表7所示，其计算结果与试验结果的对比如图11所示.

由图11可知，修正公式的计算结果与试验结果较为接近.因此，以桩体主要变形区的总约束力展开计算，可有效对桩体承载力做出评价.

2.3 不同桩径的桩体承载力研究进行不同桩径的桩体承载力推导时，取图12所示的单元体为研究对象，展开再生混凝土骨料包裹桩的弹塑性分析.桩顶荷载作用下，桩体主要发生竖向和径向的变形，切向的变形较小可忽略不予考虑，因此，柱坐标下单元体的平衡微分方程为

5.思想和行为变得早熟。受网络等媒体、社会、家庭等因素影响，学生在目标追求、思想意识、兴趣爱好、言行举止等方面出现多元化趋势，思想行为早熟。

(10)

假设单元体变形前后的体积不发生改变，则桩体单元体积满足

πr2h=π(r+Δr)2(h-Δr)，

(11)

其中，r为桩体半径，h为所取单元的高度，Δr，Δh为单元体半径和高度的改变量.对式(11)整理，省略二阶微量可得[13]：

εz=-2εr

,

(12)

再生骨料包裹桩承受竖向荷载作用时，桩土接触面满足变形协调条件，由广义胡克定律可得

σr=σθ

,

(13)

此时，桩体鼓胀变形区达到极限状态，桩体骨料颗粒满足莫尔库伦破坏准则

τzr=cc+σztanφc

,

(14)

且单元径向应力σr和竖向应力σz满足

σr=σztan2(45°-φc/2)-2cctan(45°-φc/2)

,

(15)

联立(10)和(12)～(14)可得

(16)

对式(16)进行微分方程求解

(17)

其中，γc为再生骨料重度,C为任意常数.

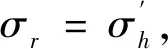
(18)

联立式(14)和(17)得

(19)

其中，B=tan2(45°+φc/2)，A=tan2φc·B.

对式(19)进行计算深度内桩体的体积积分可得出桩顶的极限荷载pv,

(20)

不同桩径的桩体承载力计算结果与试验结果如表8所示.

表8 极限承载力计算结果

由表8可知，计算值与试验值之间的误差值随着桩径的增大逐渐减小.为分析该原因，试验后在模型开挖过程中发现，桩径为56 mm和70 mm的再生混凝土骨料包裹桩在桩身100 ～300 mm的深度内发生了不同程度的局部弯曲，而桩径为100 mm和115 mm的桩体，桩身只发生不同程度的鼓胀变形未有弯曲现象产生，4种桩体的实际变形情况及变形示意图如图13所示.

因此，小桩径桩体承载力计算值与试验值之间存在较大误差，是由于小直径桩体承载过程中发生弯曲，导致桩顶荷载部分传递到土体中由土体承担，而理论计算中未考虑桩体局部弯曲.为使计算结果与试验结果更为接近，现对式(20)进行桩径上的修正，以考虑因桩体局部弯曲传递到土体中的竖向力Δpv.Δpv通过拟合试验结果与计算结果的差值β随长径比η的变化规律得出，拟合结果如图14所示，Δpv采用下式计算

Δpv=0.024 2η3-0.675 3η2+6.259 9η-18.912，

(21)

(22)

修正后的计算结果如表8所示，计算值与试验值的对比如图15所示.

由图15可知，计算结果和试验结果具有很好的一致性，采用式(22)能很好的展开不同桩径的再生混凝土骨料包裹桩承载力预测.

2.4 影响因素分析选取桩径d=100 mm、包裹刚度J=49 kN·m-1的桩体为研究对象，通过改变不同的γ，φ以及c值，得出3个因素的变化对桩体承载力的影响，具体变化值如表9所示.

表9 不同影响因素对桩体承载力的影响

在研究影响因素对桩体承载力的影响时，在展开某一参数的计算过程中其他参数取试验参数值保持不变.通过计算结果可知，土体的重度γs,土体及芯料的内摩擦角φ以及土体的粘聚力c对桩体的承载力具有显著的影响，土体重度γs和内摩擦角φs以及桩体材料的内摩擦角φc发生变化时，桩体承载力的变化幅值相对稳定，在取值范围的误差值波动最大为3.54%.土体的粘聚力值c发生改变时，桩体承载力的具有较大的波动范围，在取值范围的误差值波动达到28.21%.因此，展开桩体承载力计算时，在考虑承载力的直接影响变量外还应充分考虑计算土体的力学属性.

3 计算实例

目前，有关包裹刚度及桩径对再生混凝土骨料包裹桩承载特性的影响，还未出现较为系统性的研究.为进一步验证桩体承载力计算方法的合理与可行性，采用文献[28]中的包裹碎石桩为例对本文提出的计算方法进行应用.该文中所用土体、桩体芯料及包裹材料的物理参数如表10所示.在研究桩径对桩体承载力的影响时，所采用的桩径分别为60 mm、80 mm、100 mm，所有桩体均采用包裹材料1进行全长包裹；研究包裹刚度的影响时包裹桩的桩径为100 mm，所有桩体均保持长径比为5.

计算对象的实测值与计算值如表10所示.由表10可知，计算值与实测值较为接近，因此本文提出的再生混凝土骨料包裹桩承载力计算方法对包裹碎石桩也较为实用，在实际工程应用中能有效的对包裹桩承载力做出计算.

表10 文献[28]中土体和芯料的物理参数

表11 实例计算结果

4.小 结

以模型试验为基础对再生混凝土骨料包裹桩的承载力展开了理论研究，采用极限平衡理论和弹塑性分析对不同包裹刚度及桩径下的桩体承载力计算公式进行推导，并以试验结果为基础对计算公式展开修正，现得出以下结论：

1) 再生混凝土骨料包裹桩的包裹材料临界刚度约为100 kN·m-1，当包裹材料刚度小于临界刚度时，增加刚度能显著提高桩体极限荷载，但极限荷载增长速率会随包裹刚度的增加逐渐减小，当包裹材料刚度增加到临界刚度以上时，进一步增加包裹材料刚度不能明显改善桩体的承载能力.

2) 试验研究发现桩径为56 mm和70 mm的桩体，所能承受的极限荷载较为接近，且试验过程中在100～300 mm深度范围内出现了不同程度的局部弯曲，桩径为100 mm和117 mm的桩体承载能力较高，试验过程中仅出现桩体上部的压实及轻微鼓胀现象，未出现局部弯曲.因此，在工程应用中，应保证再生混凝土骨料包裹桩具有合理桩径，以避免局部弯曲破坏现象的发生.

(3) 理论计算表明，桩-土自重对建筑垃圾包裹单桩影响较大，进行再生混凝土骨料包裹桩设计时应充分考虑，提高包裹材料强度和桩径是改善桩体承载性能的有效途径，通过计算实例发现，本文有关再生混凝土骨料包裹桩承载力计算方法对包裹碎石桩同样适用.因此，本文提出的方法可有效推进包裹桩的工程应用.