改进的正弦余弦算法求解广义绝对值方程的最小一范数解
2021-04-25雍龙泉贾黎延海
雍龙泉贾 伟 , 黎延海
(1. 陕西理工大学 数学与计算机科学学院, 陕西 汉中 723001;2. 陕西省工业自动化重点实验室, 陕西 汉中 723001)
广义绝对值方程是指
Ax+B|x|=b,
针对多个解的广义绝对值方程,寻找稀疏解及最小一范数解已成为当前的一个研究分支[18-19].广义绝对值方程的稀疏解即求解如下零范数优化问题
(1)
其中,‖x‖0表示向量x中非零元素个数.零范数优化是一个NP-hard问题,通常的做法是采用凸松弛技巧,把稀疏解问题L0(x)转化为如下L1(x)范数优化
(2)
L1(x)范数优化问题是一个凸优化,在一定条件下,L1(x)范数优化问题的解恰好就是原问题L0(x)的稀疏解.因此研究求解L1(x)范数优化具有重要的意义.
求解问题(2)可以采用约束优化算法、交替方向法等.笔者采用一种新型的群智能优化算法:正弦余弦算法(Sine Cosine Algorithm, 简称SCA)来寻找广义绝对值方程尽可能多的解,进而在其中选取最小一范数的解.
1 适应值函数的建立
文献[19]中给出了具有多个解的广义绝对值方程,并指出广义绝对值方程解的存在性不仅与矩阵A,B有关,与向量b也有关.针对具有多个解的广义绝对值方程,为了采用智能算法求得最小一范数解,定义智能算法的适应值函数

(3)
作为优化目标函数,当且仅当f(x)=0时,则找到广义绝对值方程的解.通过多次执行算法,就有可能找到广义绝对值方程尽可能多的解,再从中选取一范数最小的解.因此,问题的关键还是求解(3).
2 正弦余弦算法
SCA是一种新型的群智能优化算法,由澳大利亚学者 Mirjalili 于 2016 年提出[20].
SCA算法步骤:
设置参数: 种群大小N,优化问题维数D,常数a=2,迭代次数Tmax;在可行域中随机选取N个个体组成初始种群;t=1;计算当前每个个体的函数值,并记录最优个体位置P(t);
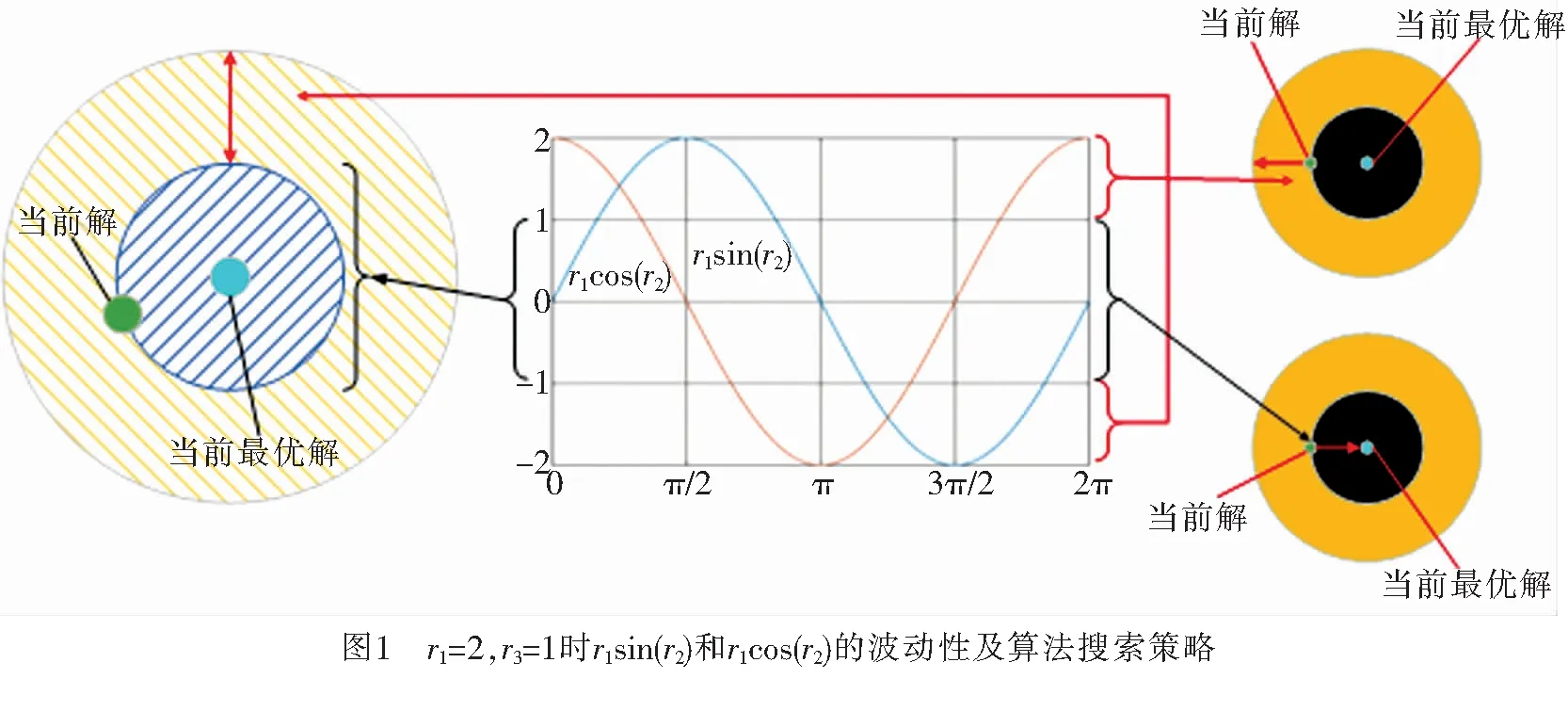
while (t fori= 1 toNdo forj= 1 toDdo 根据式r1=a-at/Tmax计算r1的值; (4) ifr4< 0.5 ; (5) else ; (6) end if end for end for 对每一个新的个体检验是否在可行域内;若不在可行域内则做越界处理; 计算每个个体的适应值并更新种群的最优个体位置P(t);t=t+1; end while SCA算法的特点是基于正弦函数(5)和余弦函数(6)值的震荡变化来达到寻优目的.在SCA算法中,参数有r1,r2,r3,r4;r1控制算法从全局搜索到局部开发的转换,r1逐渐减小;当r1>1时,函数r1sin(r2)与r1cos(r2)值才有可能大于1或者小于-1;当r1≤1时,函数r1sin(r2)与r1cos(r2)值必在-1和1之间[21].SCA算法设计原理,当|r1sin(r2)|>1或者|r1cos(r2)|>1时,算法进行全局搜索;当|r1sin(r2)|≤1或者|r1cos(r2)|≤1时,算法进行局部开发,如图1所示. SCA提出至今已经3年多,发展迅猛,更多的SCA算法见文献[22-25].参数r1线性递减,控制着算法的搜索过程.因此,对控制参数r1的改进需要进一步研究,可以进一步考虑非线性递减的函数,如抛物线函数、指数函数等来改进r1. 表1中给出了更多参数r1的表达式.图2~3给出了r1的图像. 表1 控制参数r1的表达式 将2个广义绝对值方程的算例转化为无约束优化(3),采用SCA和ISCA算法求解,程序用MatlabR2009a编写,参数设置N=30,a=2,Tmax=10 000,例1和2搜索空间为-7≤xi≤7. 例1 考虑广义绝对值方程:Ax+B|x|=b,, 其中 分别采用SCA与ISCA计算可知该问题的2个解为 其中,x(1)为最小一范数解. 2种算法都能获得该问题的最小一范数解,图3给出了2种算法的收敛性曲线. 例2 考虑广义绝对值方程:Ax+B|x|=b,其中 分别采用SCA与ISCA计算可知该问题的4个解为 其中,x(2)为最小一范数解. 2种算法都能获得该问题的最小一范数解,图4给出了优化问题目标函数的图像及2种算法的收敛性曲线. 综合图3和图4可知,相同条件下,ISCA算法收敛优于SCA.最小一范数解与稀疏解具有一定的内在关系,但是二者并不等价.已有结果表明在有限等距性质(Restricted Isometry Property, RIP)和有限等距常数(Restricted Isometry Constant, RIC)条件下,最小一范数解和稀疏解的等价性[26-27].因此,通过研究最小一范数解,可以为研究稀疏解提供一些近似结果.
3 改进的正弦余弦算法



4 数值算例




