齿轮图的星边染色

张东翰

(商洛学院 数学与计算机应用学院，陕西 商洛 726000)

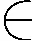
1 主要定义和引理

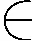
图G的一条边e称为被剖分，是指删除其并加上连接其2个端点的一条长为2的路.

2 主要结果

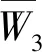
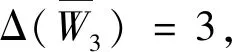
f(v0vi)=i(i=1,2,3),f(v1u1)=3,f(v2u2)=1,f(v3u3)=2,f(u1v2)=f(u2v3)=f(u3v1)=4，

证毕.

情形1v1u1染颜色2

u1v2只能从集合{1,3,4}中选择颜色.当u1v2染颜色1时，那么v0v1u1v2v0是一个2-色圈，矛盾.当u1v2染颜色3时， 那么v1u1v2v0v3是一个2-色路，矛盾.当u1v2染颜色4时，那么v1u1v2v0v4是一个2-色路，矛盾.因此,v1u1不能染颜色2.

情形2v1u1染颜色3

u1v2只能从集合{1,4}中选择颜色.当u1v2染颜色1时，那么v2u1v1v0v3是一个2-色路，矛盾.当u1v2染颜色4时，v2u2只能从集合{1,3}中选择颜色，分v2u2染颜色3和v2u2染颜色1两种情况讨论.

情形1)v2u2染颜色3

u2v3只能从集合{1,2,4}中选择颜色.当u2v3染颜色1时，那么v1v0v3u2v2是一个2-色路，矛盾.当u2v3染颜色2时，那么v2u2v3v0v2是一个2-色圈，矛盾.当u2v3染颜色4时，那么v2u2v3v0v4是一个2-色路，矛盾.

情形2)v2u2染颜色1

为了保证星边染色的条件，很容易看出u2v3只能染颜色4，v3u3只能染颜色2，u3v4只能染颜色1,v4u4只能从集合{2,3}中选择颜色.当v4u4染颜色2时，那么u4v4v0v2u1是一个2-色路，矛盾.当u4v1染颜色3时，那么u4v4v0v3u2是一个2-色路，矛盾.

因此，v1u1不能染颜色3.

情形3v1u1染颜色4

此时可以用情形2相同的分析方法而得出矛盾.

f(v0vi)=i(i=1,2,3,4),f(v1u1)=f(u2v3)=4,f(u4v1)=f(u1v2)=3,

f(v3u3)=f(v4u4)=5,f(v2u2)=1,f(u3v4)=2,

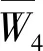
证毕.

f(v0vi)=i(i=1,2,3,4,5),f(v1u1)=f(v4u4)=3,f(u1v2)=f(u5v1)=4,

f(v2u2)=f(u4v5)=1,f(u2v3)=f(u3v4)=5,f(v3u3)=f(v5u5)=2,

证毕.

证明根据引理2～4，可知当时3≤n≤5，结论成立. 下面证明当n≥6时，结论也成立.

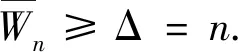
f(v0vi)=i(i=1,…,n),f(v1u1)=3,f(u1v2)=4,
f(v2u2)=1,f(u2v3)=5,f(v3u3)=2,f(u3v4)=5,

综上所述，定理1成立.

证毕.