机械臂的改进区间二型模糊神经网络控制
2021-04-25徐拥华杨永峰佃松宜
杨 威,徐拥华,杨永峰,胡 怡,佃松宜*
1.衢州光明电力投资集团有限公司赋腾科技分公司,衢州 324000 2.国网浙江电力有限公司衢州供电公司,衢州 324000 3.四川大学电气工程系,成都 610065
0 引 言
近年来,双关节机械臂被广泛应用于各个领域,提高工业生产效率.但是,机械臂的各个关节处存在耦合性,使得系统存在强非线性,而且机械臂运动过程中,难以获得完整或者全部的模型参数,也难以将模型参数视为线性函数.因此,机械臂系统中的结构和非结构的动态不确定性是双关节机械臂系统面临的典型挑战之一.
在处理不确定性和非线性的问题上,函数逼近技术可以在极小的误差范围内估计未知非线性函数.目前,自适应控制器与通用逼近器的结合已广泛应用于机械臂的轨迹跟踪控制上,常用的逼近器如神经网络[1]、自回归小波神经网络[2]、小波神经网络[3]和模糊系统[4].在文献[5]针对轨迹跟踪精度受内部摩擦和外部干扰的影响,提出一种基于径向基函数神经网络的自适应控制方法,利用RBF神经网络对机械臂的动力学模型进行辨识;在文献[6] 针对存在外部扰动及建模误差的机械臂轨迹跟踪控制问题,提出基于模糊滑模的鲁棒轨迹跟踪控制器,模糊滑模控制器采用自适应模糊逻辑修正指数滑模趋近律中的常数项;在文献[7] 针对水下复杂工作环境下机械臂控制性能易受影响,提出基于模糊RBF神经网络的智能控制器,通过模糊RBF神经网络对水下机械臂动力学方程中的水动力不确定项进行总体识别并拟合.自1965年ZADEH提出模糊集理论以来,很多研究人员证明了模糊系统具有解决高度不确定性非线性系统问题的能力[8].相比于一型模糊系统的单值前件和后件,区间二型模糊系统的区间前件和后件更适用于处理模糊信息,可看成是一型模糊系统的集合,这也说明了区间二型模糊系统处理非线性性能优异于一型模糊系统.但是,现有的区间二型模糊系统在寻找上下输出的交叉点过程中常用KM算法,而KM算法存在计算量大、耗时长的问题,导致难以应用于实际工程控制中.文献[9]中,提出了用自适应控制因子q1和q2替代KM算法.在文献[10]中,提出了利用自适应调节因子在上输出yr和下输出yl之间进行自适应调节.与自适应控制因子相比,自适应调节因子只需要更新一个自适应参数,大大减少了计算量.因此,自适应调节因子在代替KM算法上有巨大的优势.
本文将自适应调节因子应用到区间二型模糊系统中,提出带有自适应调节因子的区间而行模糊神经网络逼近器.实际上,神经网络和模糊系统在面对非线性和不确定系统时各有优缺点.神经网络的知识表示能力较差,模糊系统缺乏自学习能力.模糊神经网络是神经网络与模糊系统的融合,拥有了专家经验、模糊系统处理模糊信息的能力和神经网络的自学习能力.
基于以上讨论,本文的主要贡献是:(1)针对双关节机械臂系统,提出带有自适应调节因子的区间二型模糊神经网络逼近器的自适应反演控制方法,避免KM算法导致的计算量和耗时的问题,实现高精度、响应快的轨迹跟踪.(2)通过李雅普诺夫稳定性分析,证明了系统的有界性,同时导出了自适应律.(3)通过与一型模糊逼近器的自适应反演控制方法,仿真结果证明了所提出的控制方法跟踪性能更好.
1 改进区间二型模糊神经网络逼近器
本节介绍一个改进的区间二型模糊神经网络逼近器,如图1所示.在处理未知非线性函数上,区间二型模糊系统比一型模糊系统具有更好的逼近性能,有着明显的优势.相比于传统的二型模糊寻找上下输出的交叉点办法,本文利用自适应调节因子代替KM迭代算法,在上输出和下输出建立自适应调节,有效减小计算复杂度和耗时.
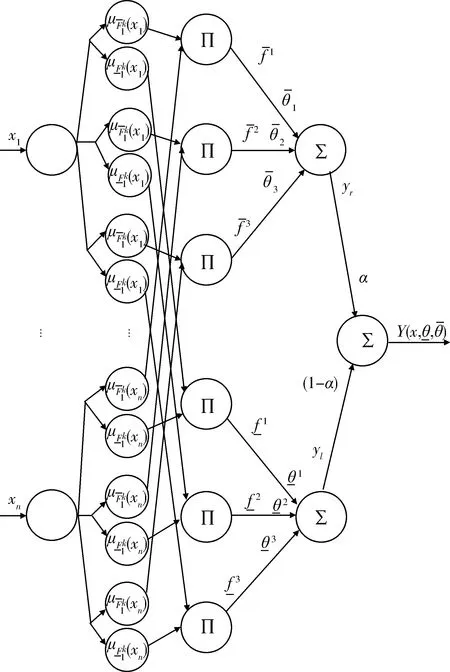
图1 改进区间二型模糊神经网络逼近器Fig.1 Improved interval type-2 fuzzy neural networks approximator
在改进区间二型模糊神经网络逼近器的规则库中,每条模糊规则是以下形式:
thenyisθkk=1,…,N
(1)
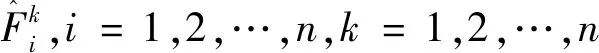
对于每一个输入向量x1,x2,…,xn,第k条规则的激活区间φk的上下界如下:
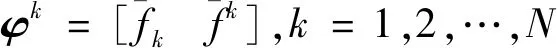
(2)
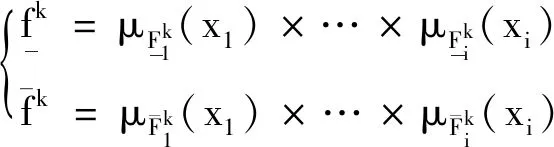
(3)
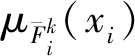
利用中心降型方法将区间模糊集变成区间单值集,具体形式如下:
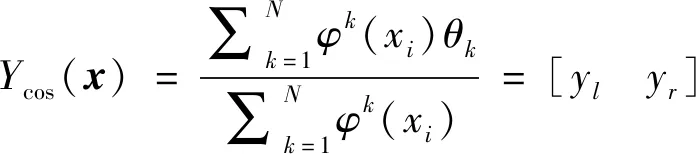
(4)
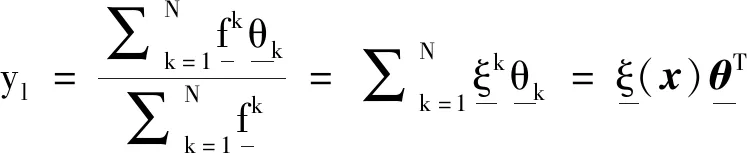
(5)
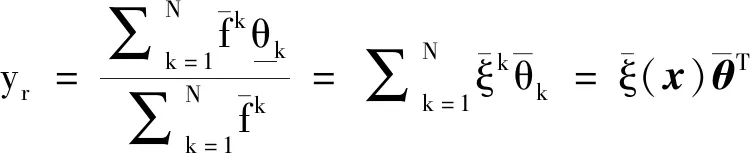
(6)
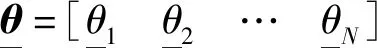
(7)
KM算法常用于确定连接下输出yl和上输出yr的交叉点,但是一般需要迭代循环2到6次才能找到交叉点,不可避免地耗时高和计算量大.自适应因子α在下输出yl和上输出yr中建立自适应调节过程,可以解决KM算法迭代计算过程的问题,提高算法实用性.
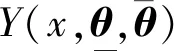
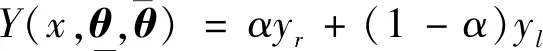
(8)
将式(5)和(6)代入(8)中,可得
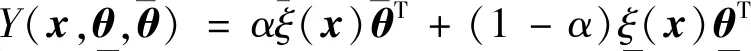
(9)
从式(9)可知,改进区间二型模糊神经网络逼近器的输出由下输出yl和上输出yr两部分组成,其中自适应因子α在下输出yl和上输出yr中建立自适应调节过程,避免KM算法带来的高计算复杂度和耗时的问题.
2 问题描述
考虑如下一类非线性双关节机械臂系统:
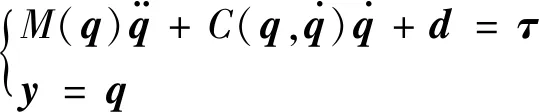
(10)
式中
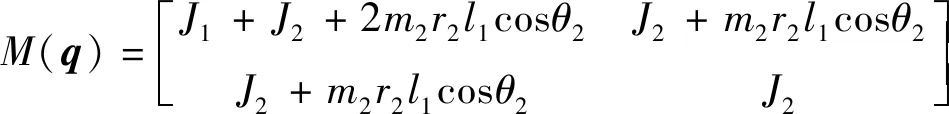
(11)
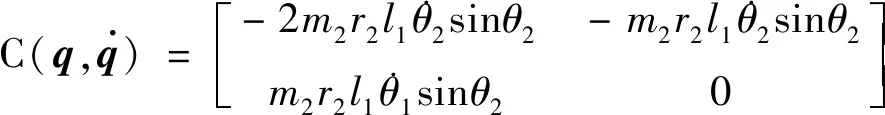
(12)
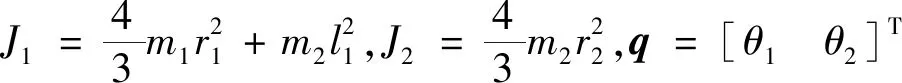
假设系统参数是未知但有界的,且系统具有如下特性:
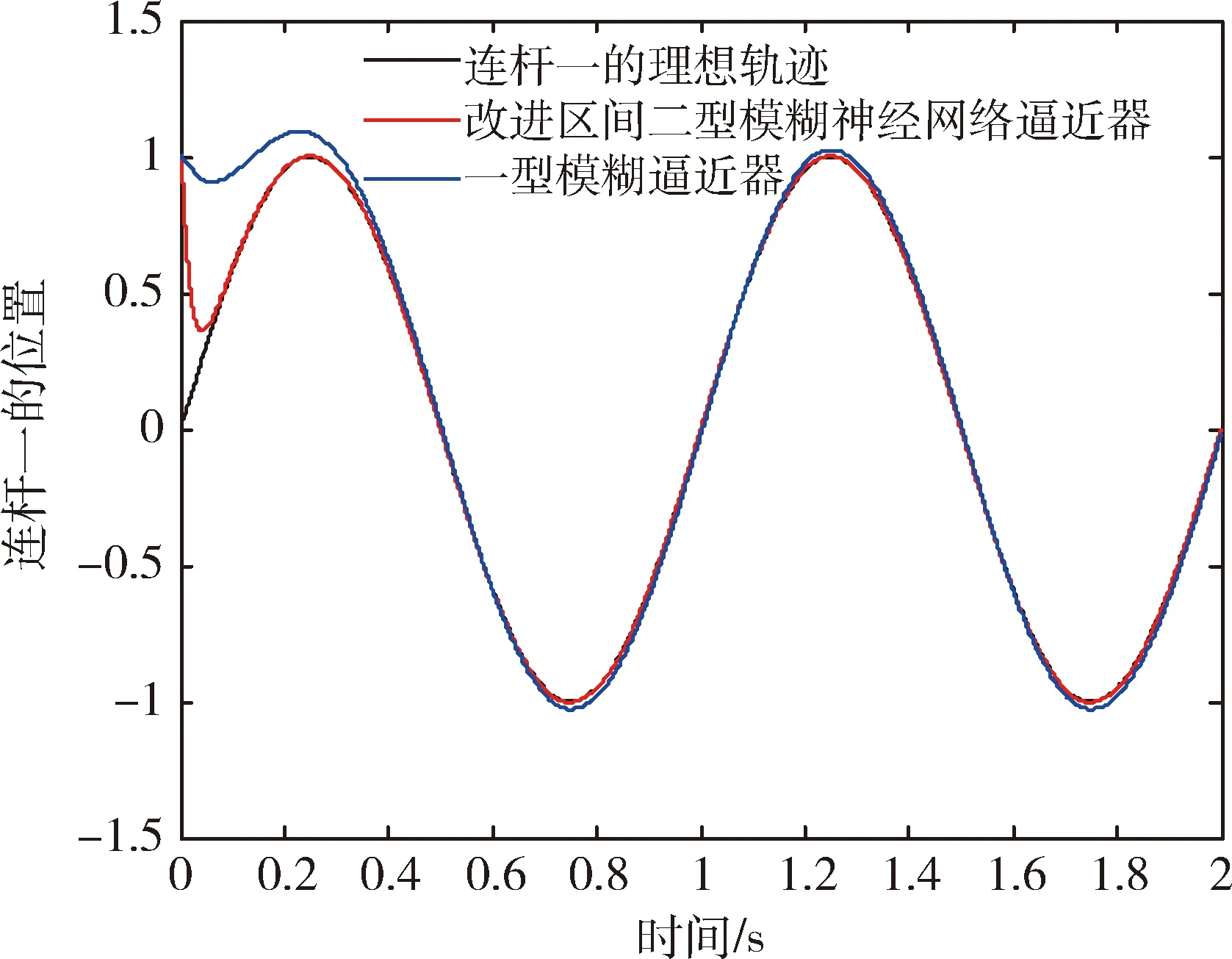
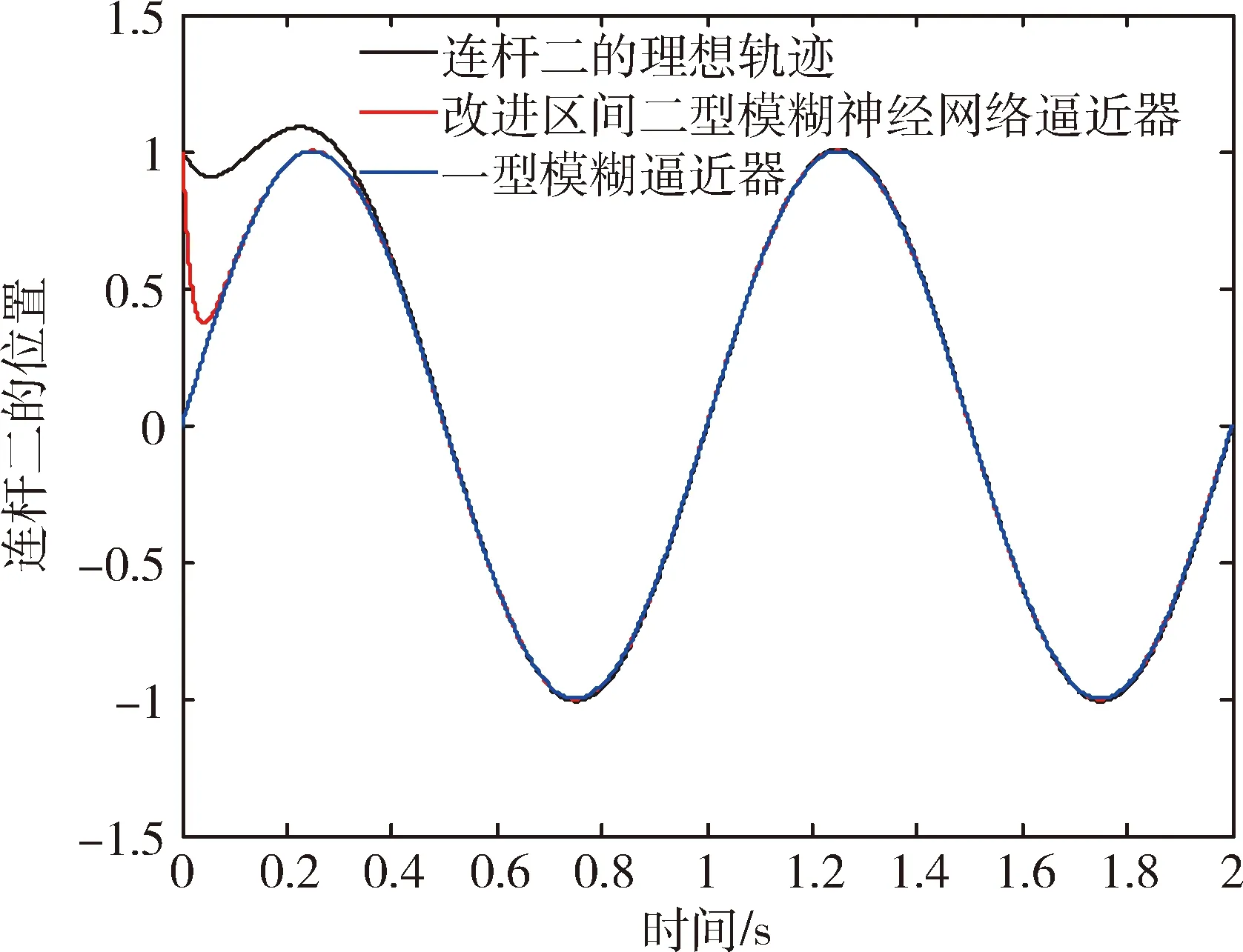
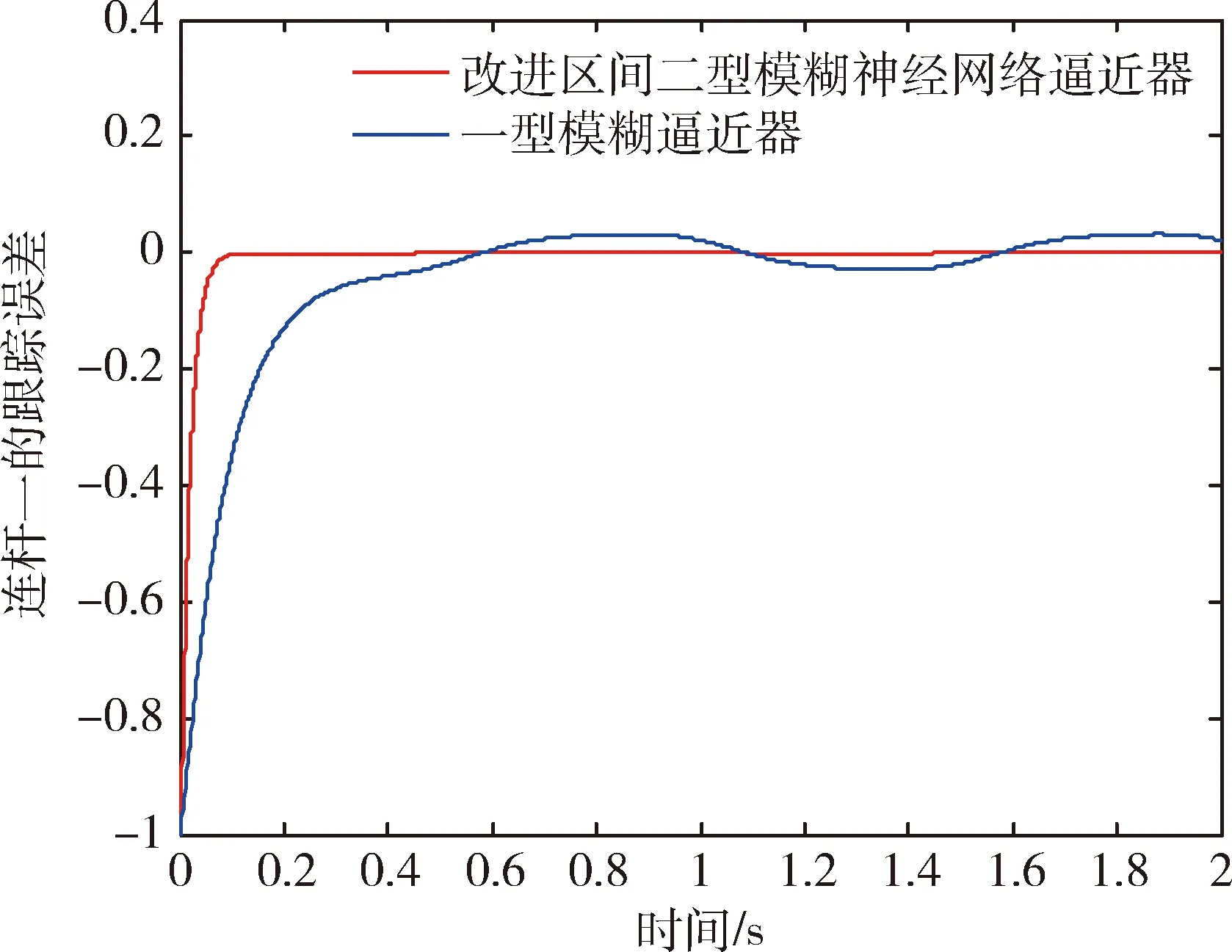
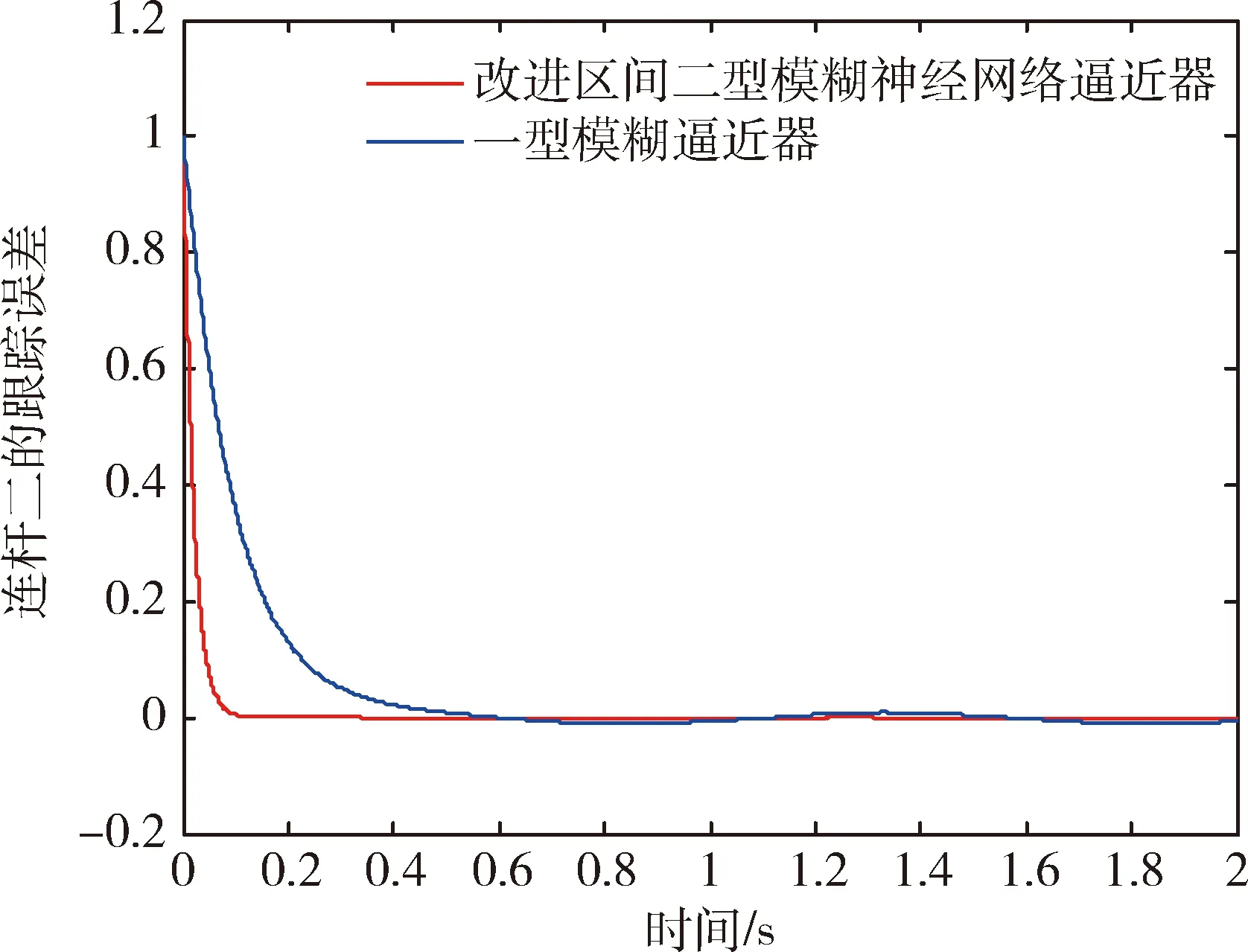
(1)惯性矩阵M(q)是正定对称矩阵并且有界,存在σ0>0,σ0∈R,则0 (13) 其中M-1(x1)和C(x1,x2)都是未知非线性函数. 在本节中,针对不确定性参数的双关节机械臂系统,设计基于改进区间二型模糊神经网络逼近器的自适应反演控制器.自适应反演控制器的设计思路分为两步. 第一步:定义误差z1=x1-yd,x1和yd分别为机械臂的角度和期望轨迹. (14) 其中λ1是一个非负常数. 由z1=x1-yd,求导可得 (15) 选择如下Lyapunov函数 (16) 对其求导可得 (17) (18) 选择如下实际控制律: τ=-λ2z2-z1-f (19) 其中λ2是一个非负常数. 选择如下Lyapunov函数 (20) 对其求导可得 (21) 将控制律(19)代入上式中,可得 (22) 由于g包含了双关节机械臂系统的惯性量以及向心力和哥氏力矩,这些属于模型信息,在实际工程中难以准确获得.因此,使用改进区间二型模糊神经网络逼近器对未知非线性函数g进行估计. 根据所提的改进区间二型模糊神经网络逼近器,则非线性函数f(x)为以下形式: (23) (24) (25) 定义如下自适应参数的控制律 (26) (27) (28) 对于整个系统,选择如下Lyapunov函数 (29) 对其求导可得 (30) 因此,可得 (31) 代入式(25)可得 (32) 则 (33) 将自适应律公式(26)-(28)代入上式可得 (34) 其中 (35) (36) (37) 定义c0=min{2λ1,2(λ2-1)/σ0,k1,k2,k3},则 (38) 假设外部干扰d∈Rn有界,因此存在D>0,满足如下不等式:dTd≤D,则 (39) 其中 (40) 解方程式(39),可得 (41) 其中V(0)为V的初始值. 由公式(41)可知,李雅普诺夫函数V(t)为非增函数,由于所有信号的有界性,根据Barbalat引理,系统渐近稳定. 在这节中,为了验证基于改进区间二型模糊神经网络逼近器的自适应反演控制算法的可行性及跟踪性能,与基于一型模糊逼近器的自适应反演控制算法进行对比.最后的仿真结果证明了所提控制算法的跟踪性能更优异,可实现高精度跟踪及快速稳定. 对于改进区间二型模糊神经网络逼近器,上下隶属函数的选取如下 (42) 系统参数选取如下:m1=0.765,m2=0.765,l1=0.25,l2=0.25,r1=0.15,r2=0.15. 图2 连杆一的跟踪曲线Fig.2 Tracking trajectory of link 1 图3 连杆二的跟踪曲线Fig.3 Tracking trajectory of link 2 图4 连杆一的跟踪误差Fig.4 Tracking error of link 1 图5 连杆二的跟踪误差Fig.5 Tracking error of link 2 为了更好直观比较两种控制算法的跟踪性能,用以下性能指标表示,分别是误差平方积分(integrated square error,ISE),误差绝对值积分(integral of absolute error,IAE)和时间乘误差绝对值积分(integrated time and absolute error,ITAE),计算公式如下: (43) (44) (45) 从以上仿真结果可以看出,基于改进区间二型模糊神经网络逼近器的自适应反演控制器在参考轨迹跟踪上有着更好的跟踪能力.即使存在外部干扰,跟踪误差也快速收敛到零的小邻域.从图4以及表1可以看出,一型模糊逼近器的跟踪误差较大,而改进区间二型模糊神经网络逼近器跟踪误差平稳,超调小,稳定时间快.以上仿真结果证明,基于改进区间二型模糊神经网络逼近器的自适应控制跟踪性能优于一型模糊逼近器,可以获得更好的稳态性能,提高逼近精度. 表1 性能指标Tab.1 Performance Index 由于双关节机械臂是一个高度非线性系统,并且难以准确获取各个模型参数信息.针对双关节机械臂的轨迹跟踪控制,本文提出基于改进区间二型模糊神经网络逼近器的自适应反演控制器,模糊神经网络是神经网络与模糊系统的融合,拥有了专家经验、模糊系统处理模糊信息的能力和神经网络的自学习能力.利用区间二型模糊神经网络逼近器估计未知非线性函数,其中的自适应调节因子取代KM算法,有效减小降型过程中的计算复杂度和耗时,增加了算法的实用性.通过李雅普诺夫方法证明了系统的稳定性.仿真结果表明,相比于基于一型模糊逼近器的自适应反演控制器,所提基于改进区间二型模糊神经网络逼近器的自适应反演控制器可实现快速响应、更短的稳定时间和更高的跟踪精度.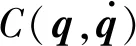
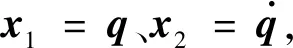
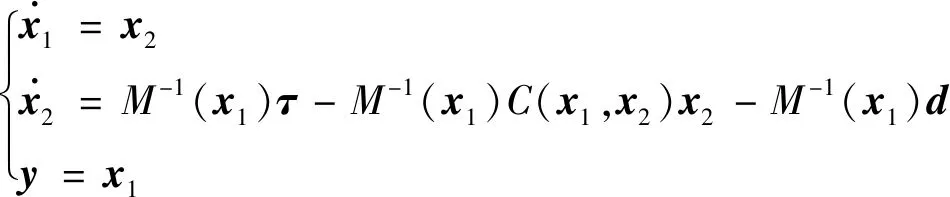
3 控制器设计
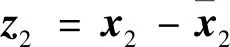
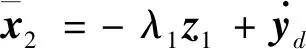
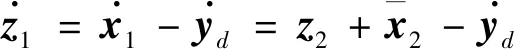
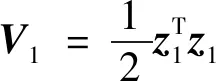
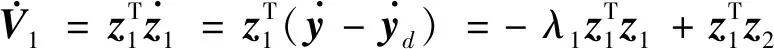
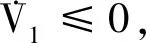
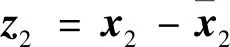
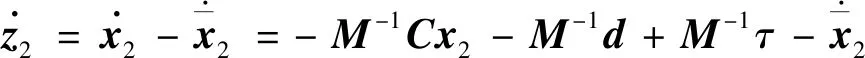
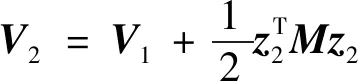
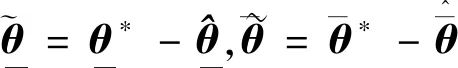
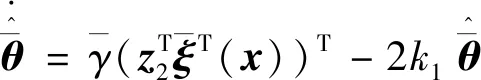
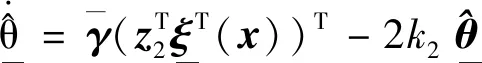
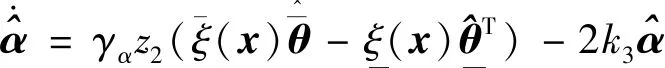
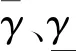
4 稳定性分析证明
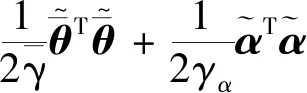
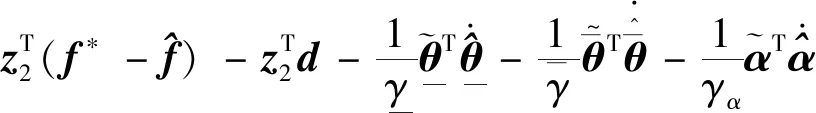
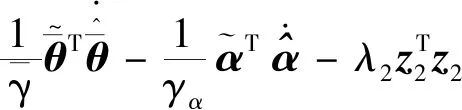
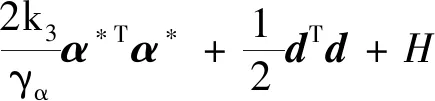
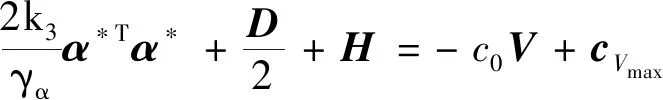
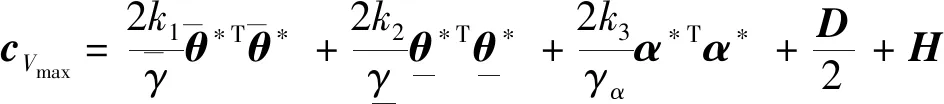
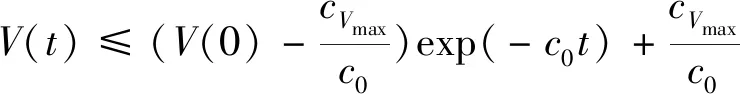
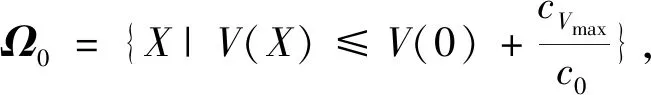
5 仿真与结果
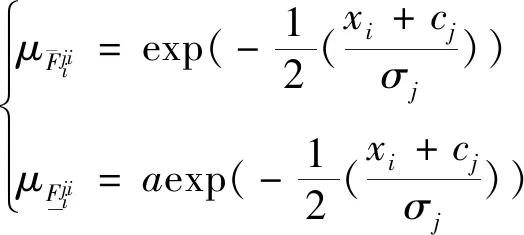
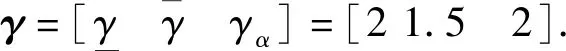
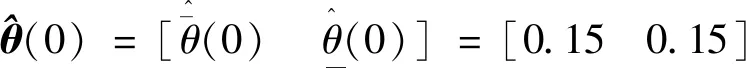
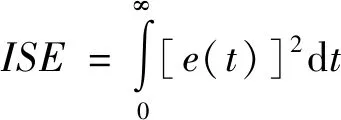

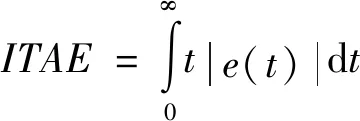

5 结束语
