近圆低轨卫星星座相位保持方法
2021-04-25王露莎李栋林
曾 光,王露莎,李栋林
航天器在轨故障诊断与维修实验室,陕西 西安 710043
0 引 言
低轨卫星星座在轨运行过程中受到地球非球形引力、日月引力、太阳光压、大气阻力等各种摄动力的影响,导致轨道高度发生衰减、相对相位发生变化,影响整个星座构型,进而影响覆盖和重访特性.当相对相位超出规定门限后,需要实施相位保持控制,确保星座构型精度维持在指标范围内.
计算星座中卫星相位偏差时需要选择一个参考基准,参考基准选择通常有两种方案,一种是在星座中选择固定的一颗卫星作为基准星,计算其他卫星的相对相位;另一种方案是基于特定的优化目标选择一个虚拟的星座基准.
如果星座有高度保持和相位保持的双重要求,在实施相位保持时需要兼顾高度保持;如果星座无高度保持要求,则可以实施单纯的相位保持控制.本文的研究针对的是后一种情况.
关于星座相位控制,文献[1]针对低轨Walker星座研究了星座构型演化及相应的维持策略;文献[2-3]结合摄动分析讨论了导航卫星星座相位保持的初值偏置问题;文献[4-5]研究了卫星星座的站位保持技术;文献[6]提出了一种基于动态调整参考轨道的星座相对相位保持策略;文献[7]提出了一种由相对相位变化量间接求取半长轴偏差,采用极限环控制的相对相位自主保持策略;文献[8]通过分析国内外星座控制技术,总结了星座的控制策略.本文在这些研究成果的基础上,进一步按照星座各星轨道衰减一致和不一致两种情况,分别提出了参考固定基准星和虚拟基准星的相位保持策略,同时分析了实际控制误差对控制策略选择的影响,最后通过仿真算例对两种策略进行比较.
1 数学模型
1.1 卫星相位漂移特性
地球J2非球形引力摄动是低轨卫星轨道的最主要摄动因素,而其余摄动项均为地球J2非球形引力摄动的二阶以上小量.对于近圆轨道,地球J2项非球形引力引起的轨道平均根数摄动变化率为[9]:

(1)

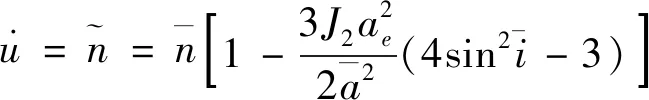
(2)
式(2)表明,对于近圆轨道,考虑地球J2项非球形摄动,卫星相位长期变化率与卫星平半长轴和平轨道倾角有关.
如果低轨卫星星座中的所有卫星标称轨道倾角一致,则星座中卫星的平半长轴差异是引起星座构型漂移的主要因素.低轨卫星平半长轴变化主要受到大气阻尼摄动影响,一个轨道周期时间内,大气阻力引起的轨道平均半长轴衰减量为:

(3)
式中,CD为大气阻尼系数,A/m为卫星面质比,ρ为大气密度.如果星座中卫星面质比存在差异,则卫星半长轴衰减率不一致,进而会导致星座构型发生漂移.
1.2 卫星相位偏差表达式
1.2.1 参考固定基准星
参考固定基准星的方法需要在星座中选择一颗基准星j,基准星不控.参考固定基准星时,相位偏差的计算方法如下:
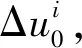

(4)
星座中其他卫星相位偏差为:

(5)
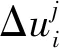
1.2.2 参考虚拟基准星
参考虚拟基准星的方法是根据星座中所有卫星实际相位,依据优化规则实时构造虚拟的星座构型,所有的卫星相位偏差都是相对于这个虚拟的星座构型.参考虚拟基准星时,相位偏差的计算方法如下:
(1)计算虚拟基准星的相位
(6)
指标函数U最小的条件是:

(7)
解算式(7)得到b的最优值为:

(8)
(2)计算所有卫星相对于虚拟基准的相位偏差分别为:

(9)
1.3 卫星相位偏差演化
1.3.1 参考固定基准星
根据参考固定基准星的相位偏差计算方法,设基准星为j,星座初始状态为:

(10)

(11)
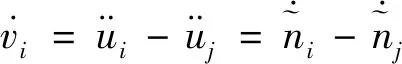
(12)
1.3.2 参考虚拟基准星
根据参考虚拟基准星的相位偏差计算方法,设星座初始状态为:

(13)

(14)
对于近圆轨道有:

(15)
1.4 相对相位保持方法
1.4.1 各星衰减率一致条件下保持策略

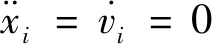
(16)

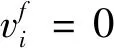
(17)
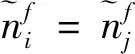
(18)
也就是说,当星座中第i颗星的相对相位偏差超出门限值时,在忽略控制误差时,第i颗星的目标角速度为基准卫星的角速度.
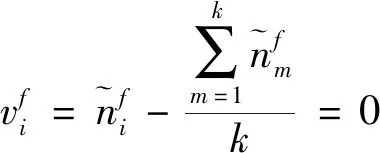
(19)
进而得到:
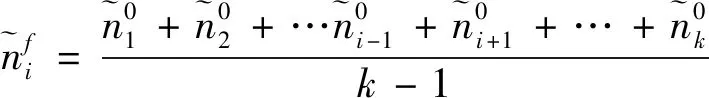
(20)
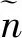
1.4.2 各星衰减率差异条件下保持策略
当参考固定基准星时:

(21)
当参考虚拟基准星时:

(22)

(23)
从上式可以看出卫星控后相位差变化趋势是一条抛物线.下面分两种情况进行讨论:
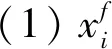
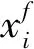

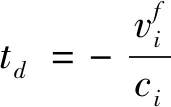
(24)
代入式(23),得

(25)

当ci>0时

(26)
当ci<0时
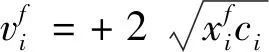
(27)
当参考固定基准星时,卫星i理论控后角速度为
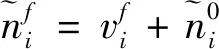
(28)
理论控后角速度为
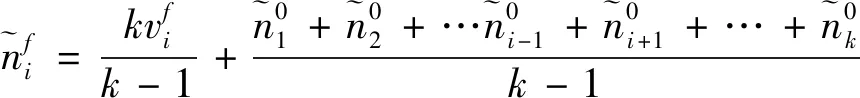
(29)

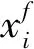
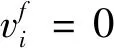
(30)
当参考固定基准星时,卫星i理论控后角速度为:

(31)
理论控后角速度为:
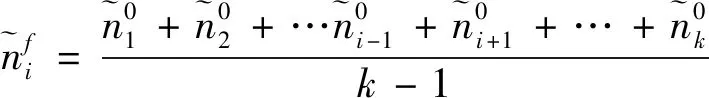
(32)
1.5 考虑控制误差的保持策略
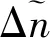

(33)

(34)
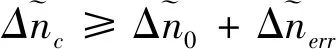
(35)

(36)


(37)

图1 衰减率一致条件下控制效果Fig.1 Control effects under the condition of consistent rate of decay

图2 衰减率不一致且和ci正负同号条件下控制效果Fig.2 Control effects under the condition of inconsistent rate of decay and the same positive or negative signs of and ci
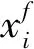
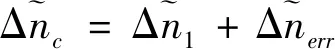
(38)
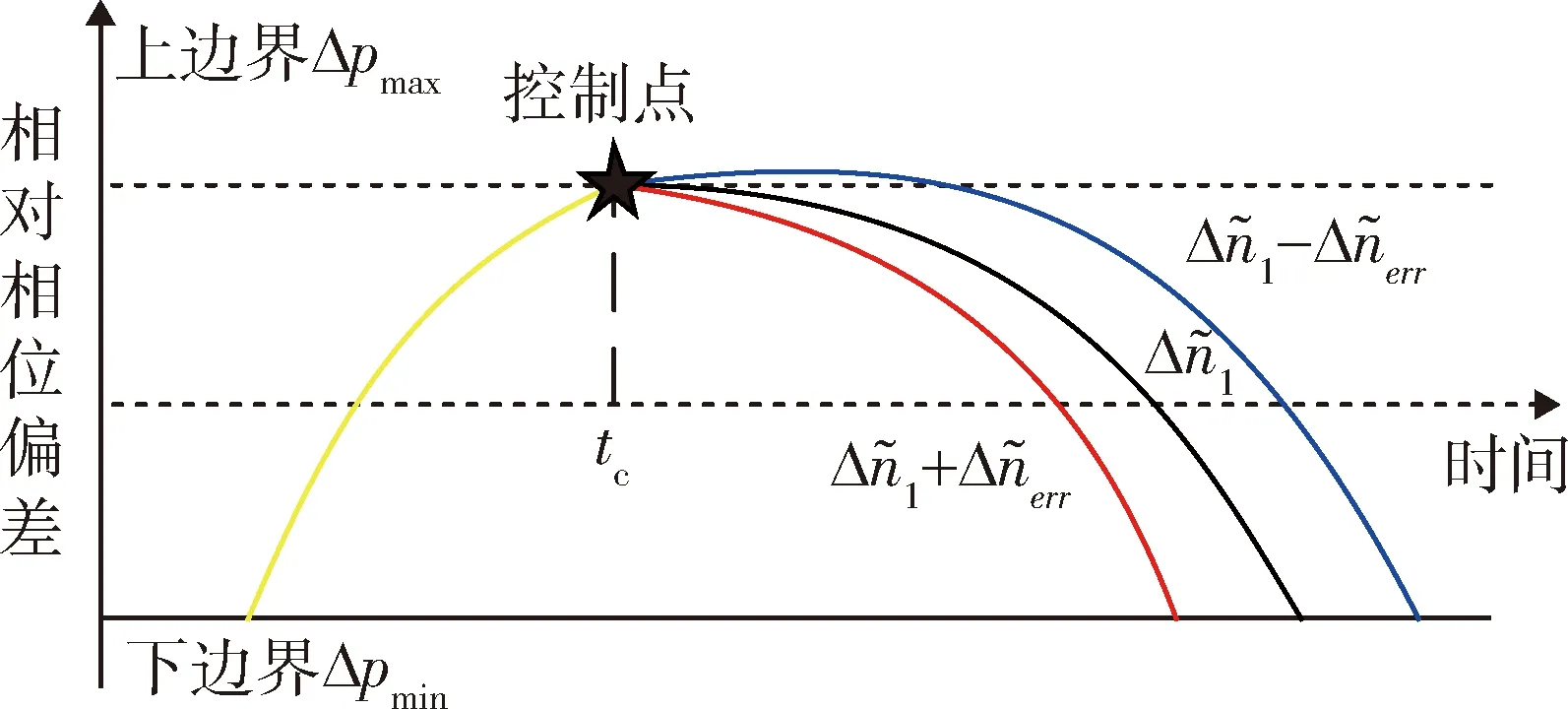
图3 衰减率不一致且和ci正负异号条件下控制效果Fig.3 Control effects under the condition of inconsistent rate of decay and the different positive or negative signs of and ci
2 仿真计算
2.1 仿真方案
以参考码为18/3/1的Walker星座为研究对象,轨道倾角为55°,相位保持范围为±4°,标称轨道高度900 km.
设星座组网后各星初始半长轴为6378140 m±50 m的随机变量,初始相位偏差为±4°的随机变量,卫星每次的控制误差为±15 m的随机变量.轨道预报采用解析法,考虑地球非球形摄动、日月引力摄动、大气阻尼摄动、太阳光压摄动.
分两种情况进行仿真,一种是星座内各星半长轴衰减率一致,另一种情况是星座内各星半长轴衰减率存在差异,但均为常数.分别在这两种情况下仿真参考固定基准星和参考虚拟基准星两种相位保持控制方法在控制频率、控制量上的差异.
2.2 仿真结果
仿真条件1:星座中各星轨道衰减率一致将星座中各星轨道周期变率均设置为-0.0001 s/天,仿真计算20年内星座相位保持情况.分别用参考固定基准星(第一颗星)和参考虚拟基准星的方法仿真星座中各星的相位偏差的演化过程,当相位偏差超过门限(±4°)时,按照式(18)和式(20)给出的控制量实时相位保持控制,仿真控制效果时考虑控制误差影响(实际控制量=理论控制量+随机控制误差).参考固定基准星的仿真结果如图4所示,参考虚拟基准星的仿真结果如图5所示(每个平面选择一颗星展示).从图中可以看出,两种方法均有效,都可以满足相位保持要求.
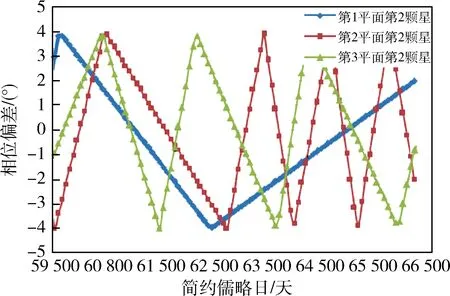
图4 衰减率一致条件下参考固定基准星的仿真结果Fig.4 The simulation results with the fixed reference star under the condition of consistent rate of decay

图5 衰减率一致条件下参考虚拟基准星的仿真结果Fig.5 The simulation results with the virtual reference star under the condition of consistent rate of decay
为分析两种方法在控制频率和控制总量上的差异,共仿真100组不同初值状态下情况取平均值,参考固定基准星方法控制次数平均为61.1次,半长轴控制总量平均为1598.1 m;参考虚拟基准星方法控制次数平均为63.4次,半长轴控制总量平均为1641.2 m.统计结果如图6~7所示.

图6 轨道衰减率一致条件下控制次数比较Fig.6 The comparison of control times under the condition of consistent rate of decay
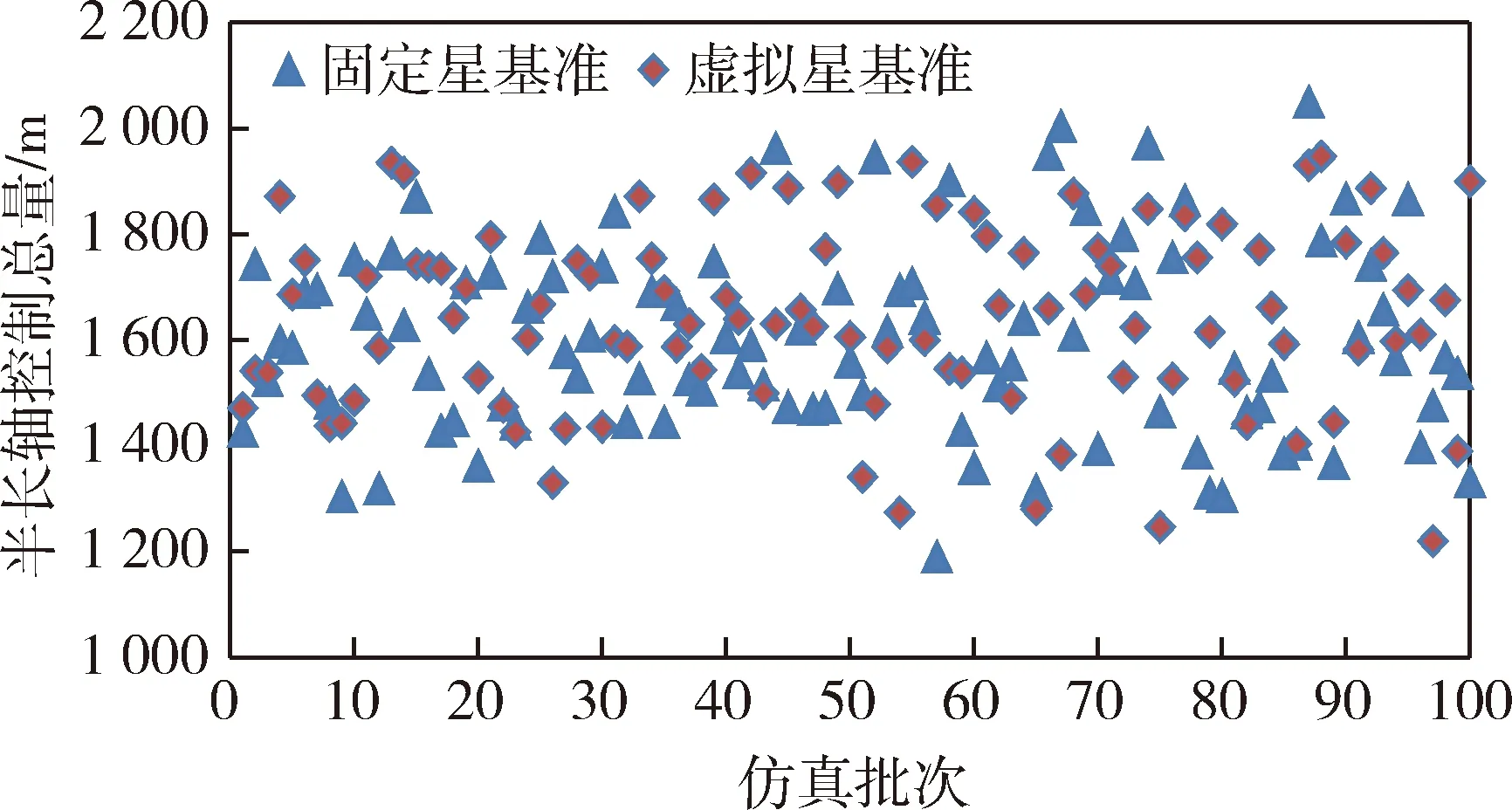
图7 轨道衰减率一致条件下燃料消耗比较Fig.7 The comparison of fuel consumption under the condition of consistent rate of decay
仿真条件2:星座中各星轨道衰减率存在差异
为仿真轨道衰减率存在差异的情况,星座中各星轨道周期变率在-0.003 s/天~0.0 s/天之间随机产生,仿真计算10年内星座相位保持情况.其它仿真条件同仿真条件1.按照式(28)、式(29)、式(31)和式(32)给出的控制量实时相位保持控制,仿真控制效果时考虑控制误差影响.参考固定基准星的仿真结果如图8所示,参考虚拟基准星的仿真结果如图9所示.从图中可以看出,两种方法均有效,都可以满足相位保持要求.

图8 轨道衰减率不一致参考固定基准星的仿真结果Fig.8 The simulation results with the fixed reference star under the condition of inconsistent rate of decay
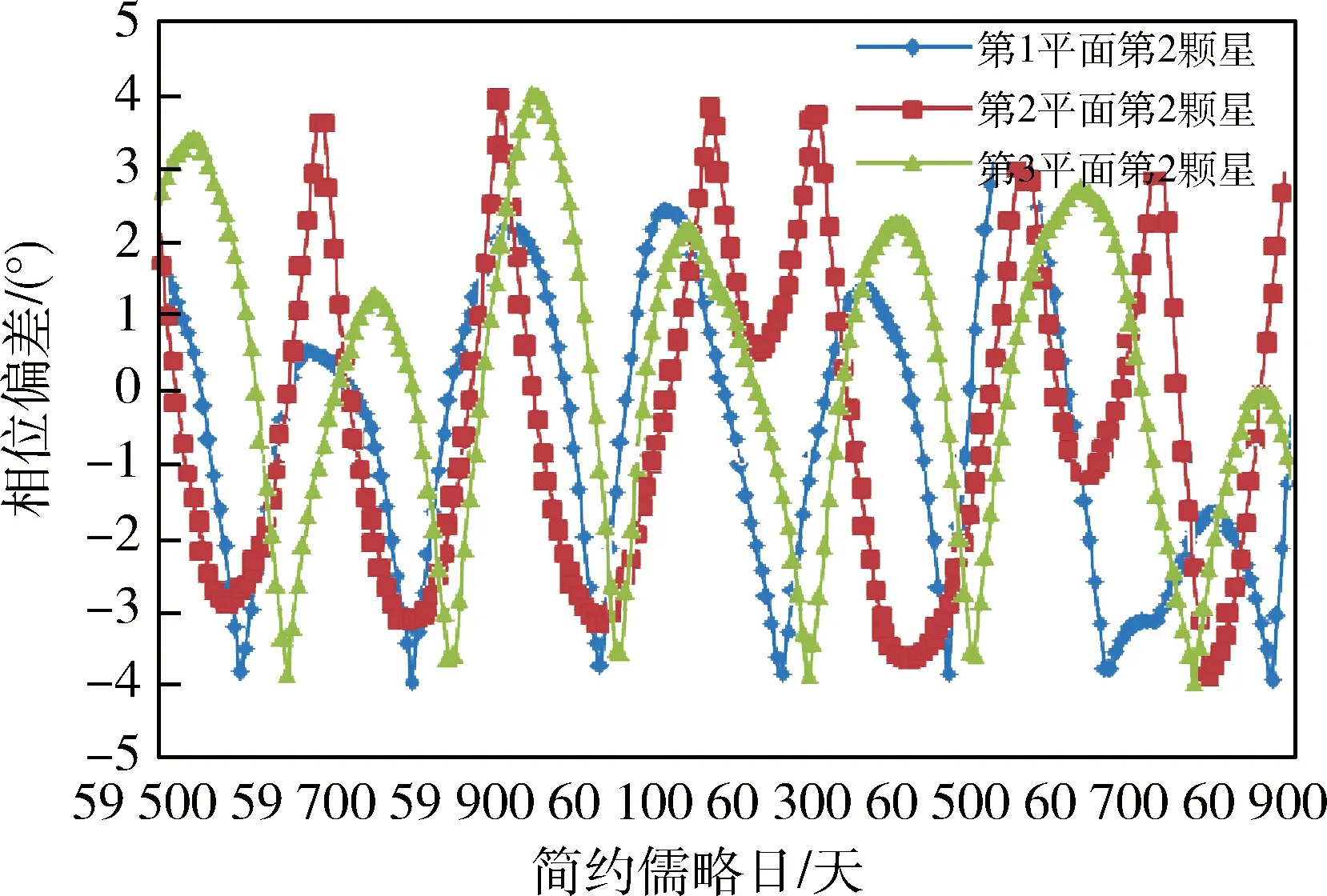
图9 轨道衰减率不一致参考虚拟基准星的仿真结果Fig.9 The simulation results with the virtual reference star under the condition of inconsistent rate of decay
为分析两种方法在控制频率和控制总量上的差异,共仿真100组不同初值状态下情况取平均值,参考固定基准星方法控制次数平均为242.8次,半长轴控制总量平均为37067.9 m;参考虚拟基准星方法控制次数平均为328.2次,半长轴控制总量平均为46538.8m.统计结果如图10~11所示.
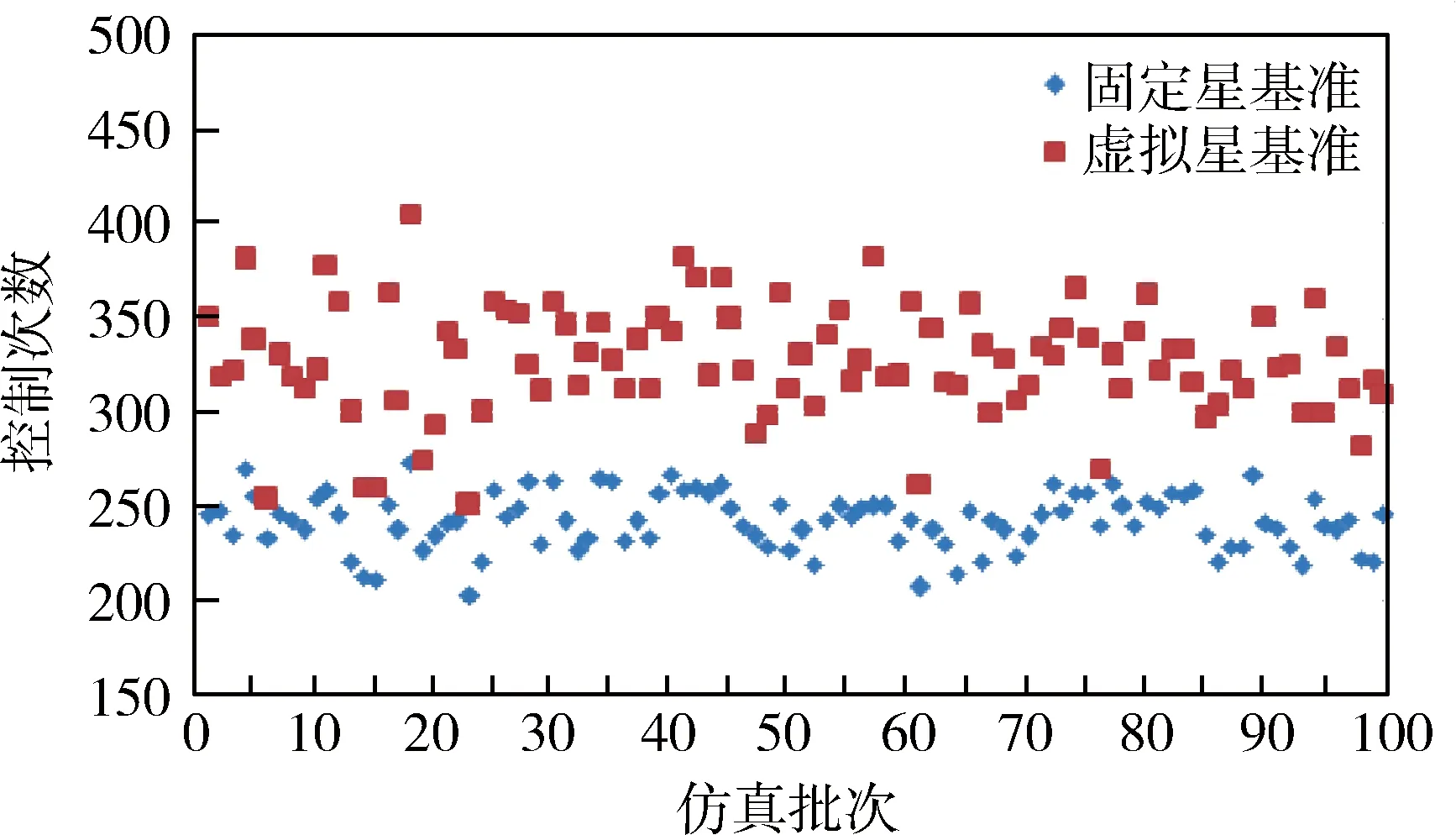
图10 轨道衰减率不一致条件下控制次数比较Fig.10 The comparison of control times under the condition of inconsistent rate of decay

图11 轨道衰减率不一致条件下燃料消耗比较Fig.11 The comparison of fuel consumption under the condition of inconsistent rate of decay
3 结 论
本文研究了无轨道高度保持要求的低轨星座相位保持控制方法,按照星座中各星轨道衰减一致和不一致两种情况,分别提出了参考固定基准星和虚拟基准星的相位保持策略,经过仿真分析可以得到如下结论:
1)星座中各星轨道衰减率一致,或星座中各星轨道衰减率存在差异,参考固定基准星和参考虚拟基准星两种相位保持控制方法均能够完成日常相位保持任务
2)星座中各星轨道衰减率一致时,参考固定基准星和参考虚拟基准星两种相位保持控制方法在控制频率、控制量上无显著差异;
3)星座中各星轨道衰减率存在差异时,参考固定基准星在控制频率、控制量上明显优于参考虚拟基准星相位保持控制方法.
