一种小行星探测陆标导航方法

张成渝，梁 潇，华宝成，武延鹏，王安然，张依诺

北京控制工程研究所,北京 100090

0 引 言

小行星探测任务已经被列入中国深空探测4次重大任务[1]，通过一次发射实现近地小行星2016HO3取样返回和主带彗星133P绕飞探测.小行星的各种特性不确定性高，需要接近小行星进行观测与建模.利用小行星表面特征建立导航陆标，结合实时观测图像给出精确导航结果.小行星探测下降着陆段的精确相对导航是小行星探测任务的一个关键技术，影响任务的成败.

在小行星探测下降着陆段，距离小行星过近，小行星的亮度增加，并且逐渐扩充整个相机视野，此时基于恒星参考的光学导航失效了.同时，小行星的表面特征显现出来，可以将这些特征作为陆标，用来确定航天器的位姿[2].以往探测任务表明，小行星下降着陆段大多采用基于陆标参考的光学导航，即陆标导航，部分任务情况如表1所示[3-11].

表1 部分小行星探测任务陆标导航简介Tab.1 Introduction to landmark navigation of some asteroid exploration missions

由GASKELL[12-13]提出的高精度三维重建方法Stereophotoclinometry (SPC)，可以生成一种广义表面特征SPC陆标(L-map/maplet).BHASKARAN等[14]提出的On-Board Image Registration for Optical Navigation(OBIRON)系统，是一种基于SPC的地面导航技术.利用NEAR和MUSES-C[15]探测任务的图像进行了地面测试，在Dawn探测任务中作为地面光学导航方法.OSIRIS-Rex探测任务由Lockheed Martin(LM)[16-17]公司开发的自然特征跟踪(NFT)，是一种基于SPC陆标的星载光学导航方法.基于SPC陆标的导航方法，通过多次探测任务不断发展，已经成为一种自主实时高精度导航方法.

国内众多学者也对小行星探测下降着陆段的光学导航进行了研究.黄翔宇等[18]提出了利用激光测距仪和光学导航相机测量三个特征点的图像坐标和到探测器的距离，由此得出探测器的相对位置.邵巍等[19]提出了一种利用PCA-SIFT算法提取的特征点作为导航陆标，并结合三维模型和虚拟拼接地图进行探测器自主着陆的导航算法.

上述基于SPC陆标的导航方法仅适用于初始相机位姿偏差较小的情况，因为图像相关匹配的搜索范围最大为陆标图像.而实际导航过程中，会出现初始相机位姿偏差较大的情况，需要扩大相关匹配搜索范围.本文提出一种基于SPC陆标的高精度导航方法，通过初始相机位姿渲染陆标的预测图像和生成陆标的提取图像，并进行图像匹配，得到亚像素精度的陆标中心点图像位置，再结合三维位置即可解算相机位姿.将相关匹配搜索范围扩展到整个观测图像，在初始相机位姿偏差较大时也满足要求.

1 陆标导航

对于小行星下降着陆过程，陆标导航将几个(大于3)陆标中心点作为观测点，求解航天器位姿，如图1所示.如果能得到高精度的陆标中心点3D-2D点对，显然利用陆标导航求解的位姿精度也高.本文主要研究如何根据陆标地形模型确定高精度陆标中心点图像位置.

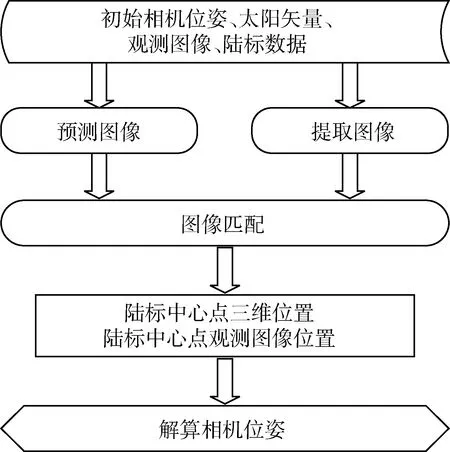
图1 陆标导航Fig.1 Landmark navigation

首先，利用初始相机位姿、太阳矢量和陆标数据，渲染陆标的预测图像.其次，利用初始相机位姿和陆标数据，从观测图像中生成陆标的提取图像.然后，将预测图像与提取图像进行图像匹配，获取陆标中心点观测图像位置.最后，获取几个陆标中心点的3D-2D点对，利用PNP算法求解相机位姿.

陆标包括小行星表面图像中的图像特征；陨石坑、石头等小行星突出表面特征；广义表面特征，一个局部区域，而非明显的特征；甚至是人工陆标.早期常以陨石坑作为陆标，但目标天体可能不存在陨石坑，需要更广义的陆标.SPC陆标定义为小行星表面的一个小面片，一个小型数字地形模型，一般为99×99的栅格[20]，如图2所示.每个陆标包含的数据有：陆标的坐标系定义及小行星固联系下陆标中心点位置，陆标上每点的反照率数据、高程数据[21].采用SPC技术生成地形模型精度高，但陆标分辨率往往与观测图像分辨率不同.

图2 小行星表面的一个陆标Fig.2 A landmark on the surface of an asteroid

理想情况下，初始相机位姿偏差较小，即与真实相机位姿差异较小，陆标导航对初始相机位姿进行更精确修正.但实际运行中，陆标导航往往利用惯性导航等提供初始相机位姿输入，必然会出现初始相机位姿偏差较大的情况.因此陆标导航必须确保在较大偏差情况下同样满足精度要求.

1.1 图像渲染

陆标被SPC生成后，利用初始相机位姿以及太阳矢量，根据SPC光照模型，结合陆标每一点的法向量和反照率，逐点计算灰度值，直接渲染生成陆标的预测图像[22].SPC光照模型计算陆标点k处灰度Ik为

Ik=ΛakRk+Φ

(1)

式中，Λ是乘法常数，Φ是背景常数，由SPC计算或者图像标定给出.ak是点k的相对反照率，由SPC给出.Rk是Lunar-Lambert函数[23]

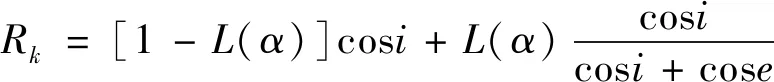
(2)

Lunar-Lambert函数是Lommel-Seeliger和Lambert反射函数的组合.其中入射角i定义为太阳方向矢量(从表面点到太阳的方向)与表面点法向量的夹角，反射角e定义为相机方向矢量(从表面点到相机的方向)与表面点法向量的夹角，相位角α定义为太阳方向矢量与相机方向矢量夹角.遵循Gaskell的惯例，L(α)的定义为：

L(α)=e-α/60

(3)

由于SPC生成的模型精度高，所以利用SPC陆标渲染预测图像具有较好的真实性，如图3(a)所示.图像渲染方法快速简单，可用于星载导航.但预测图像与陆标模型分辨率一致，不是观测图像分辨率.

1.2 图像提取

从观测图像中生成与预测图像相同分辨率的提取图像，解决预测图像与观测图像分辨率不一致问题.利用初始相机位姿和陆标数据将陆标逐点投影到观测图像中，并利用双线性插值计算灰度值，生成提取图像.由于都对陆标进行逐点运算，所以提取图像与预测图像均为陆标分辨率，如图3(b)所示.

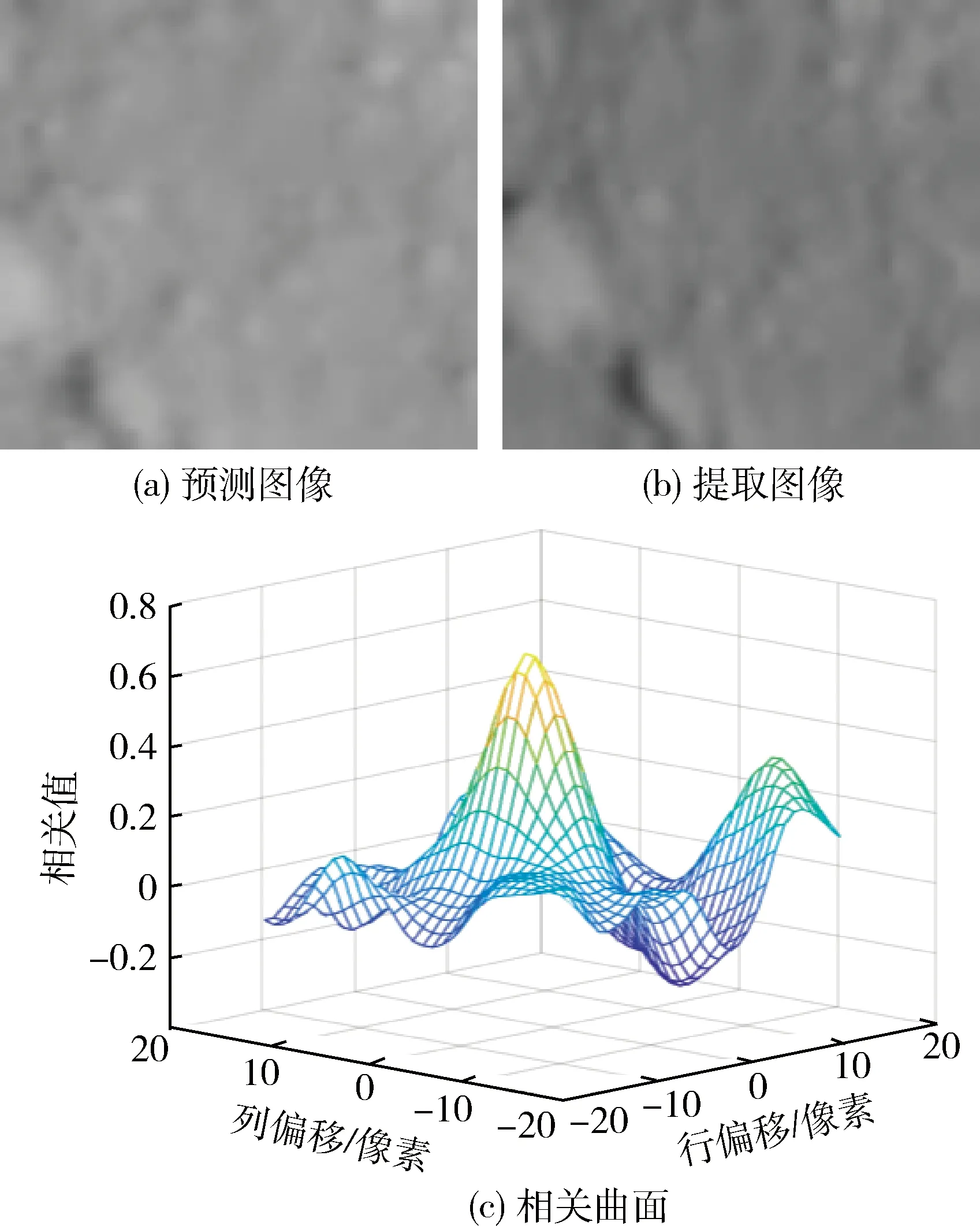
图3 陆标图像示意图Fig.3 Illustration of landmark image

利用初始相机位姿生成的提取图像，往往不能完全对应陆标，甚至远远超出陆标对应图像区域.

1.3 图像匹配

图像匹配的基本原理是对预测图像和提取图像执行相关匹配，用互相关函数来描述两幅图像的相似程度.使用归一化互相关(NCC)来计算相关系数：

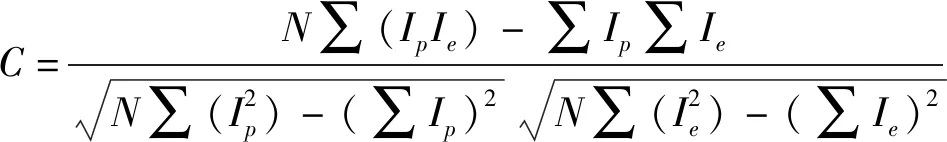
(4)

其中N是参与相关的像素数量,Ip和Ie分别是预测图像和提取图像.C为相关值，其取值范围为[-1,1]之间，便于度量相关程度.越接近1表示越相关，0.6以上即为强相关.

利用初始相机位姿可以得到陆标中心点对应的初始观测图像位置，不是最终位置.通过不断偏移预测图像，并与观测图像相关，生成一个相关曲面，如图3(c)所示.获取相关曲面的最大相关值点，该点对应的偏移为最终偏移值.陆标中心点的初始观测图像位置加上这个偏移值，就得到陆标中心点的最终观测图像位置.

本文提出一种组合相关匹配方法进行图像匹配，能够快速精准给出陆标中心点观测图像位置，并在初始相机位姿偏差较大时同样得到精确结果.

1.3.1 全局相关匹配

根据模板匹配原理，将预测图像作为模板图像，将观测图像作为搜索图像，将提取图像作为搜索子图，在观测图像上搜索与预测图像最相似的提取图像.由于搜索范围可以覆盖整个观测图像，因此称该方法为全局相关匹配.

利用初始相机位姿生成提取图像时，如果对陆标每个点投影生成的图像坐标逐点偏移，就会得到新的陆标投影坐标.再对新投影坐标利用双线性插值获得灰度值，就生成新提取图像.即通过投影坐标整体偏移，得到陆标提取图像的偏移.该方法在搜索中不断生成与预测图像分辨率一样的提取图像，保证了相关匹配的顺利进行.在不断搜索偏移过程中，生成不同提取图像，分别与预测图像进行归一化互相关，生成一个相关曲面.寻找最大相关值点，该点对应的偏移加上陆标中心点的初始观测图像位置即为最终观测图像位置.如图4所示，蓝色块表示观测图像，黄色块表示未偏移的初始提取图像，深红色块表示偏移后得到的最佳提取图像(最大相关偏移对应图像)，淡红色块表示预测图像.

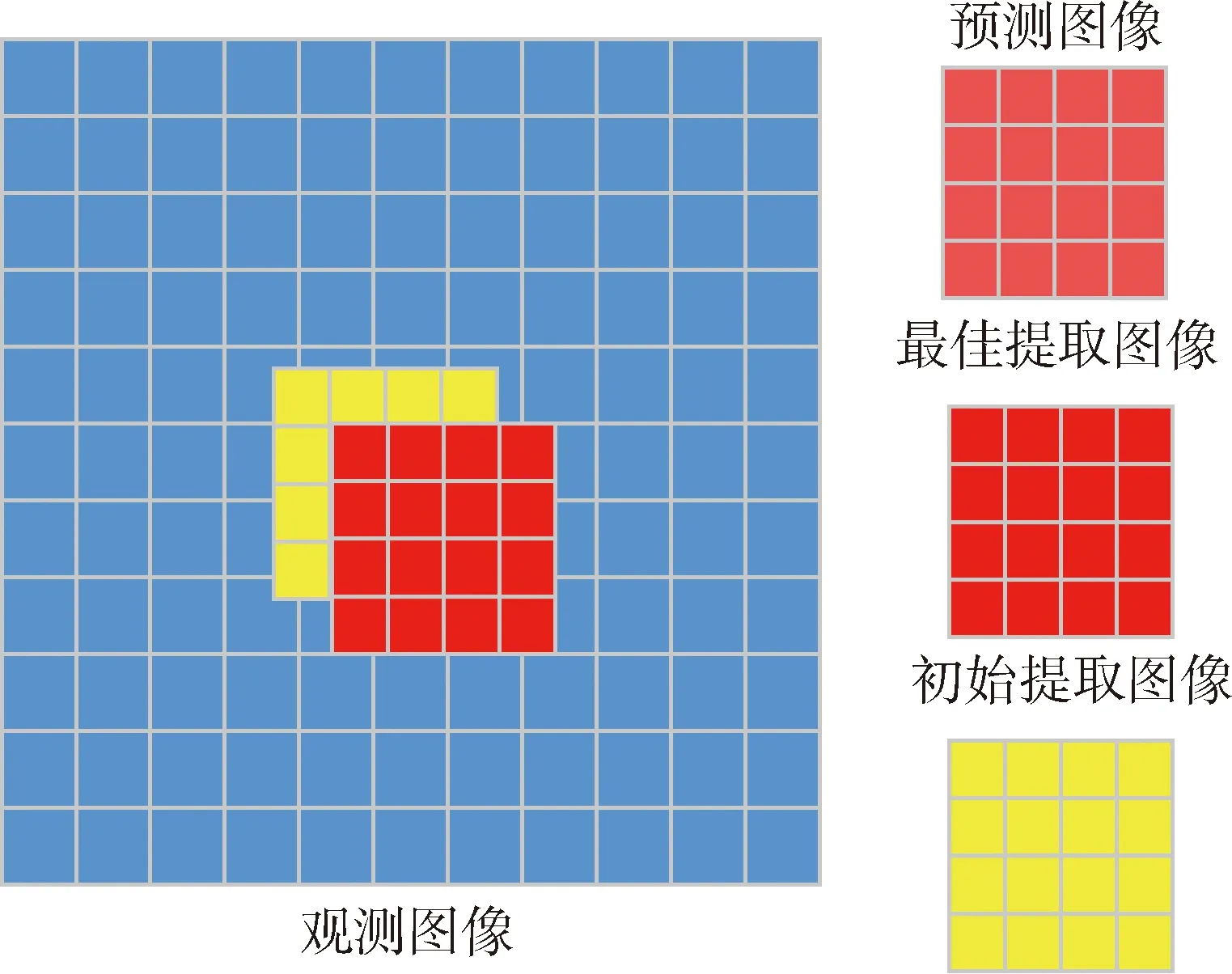
图4 全局相关匹配示意图Fig.4 Illustration of global image cross-correlation matching

1.3.2 局部相关匹配

一般而言，进行模板匹配时，搜索图像远远大于模板图像.如果将提取图像作为搜索图像，预测图像作为模板图像，此时搜索图像与模板图像大小一样，而且分辨率一致.由于最大搜索范围为提取图像大小，因此称该方法为局部相关匹配.

利用初始相机位姿生成提取图像，将预测图像在提取图像上进行相关搜索，两者重合时表示未偏移.在不断偏移过程中，产生不同的重叠部分，将提取图像与预测图像的重叠部分进行归一化互相关，如图5所示.生成一个相关曲面，寻找最大相关值，此时的偏移作为陆标分辨率下的偏移，需要转化为观测图像分辨率下的偏移.预测图像中陆标中心点对应一个提取图像匹配点，将该匹配点的观测图像位置作为陆标中心点的最终观测图像位置.

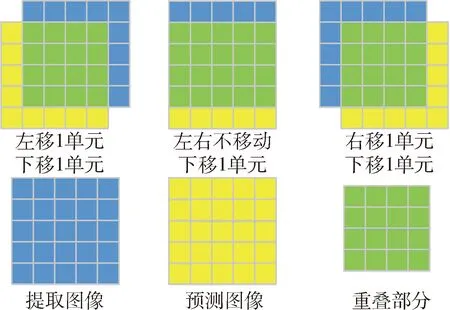
图5 局部相关匹配示意图Fig.5 Illustration of partial image cross-correlation matching

全局相关匹配的最大搜索区域为整个观测图像，参与相关计算的为预测图像和提取图像的全部像素；但是每次偏移都需要生成新的提取图像，实时性差.局部相关匹配的最大搜索区域为提取图像，参与相关计算的为预测图像和提取图像的重叠部分像素；只需要生成一张提取图像，实时性好.目前基于SPC陆标的导航方法大多采用局部相关匹配方法，由于搜索范围仅为陆标图像大小，所以仅适用于初始相机位姿较小的情况.

1.3.3 组合相关匹配

理想条件下，输入初始相机位姿偏差都较小，运用局部相关匹配即可.但探测器实际运行中，由惯性导航给出的初始相机位姿可能具有较大偏差，或者是由其它导航方法切换到陆标导航时偏差往往较大.当初始相机位姿偏差较大时，初始提取图像可能仅对应小部分陆标，甚至完全不对应陆标.局部相关匹配得不到准确解，而使用全局相关匹配扩大搜索范围能得到准确解.但是搜索范围扩大，全局相关匹配的实时性会变得极差.本文采用一种将全局相关匹配作为粗匹配和将局部相关匹配作为精匹配的组合相关匹配方法，在初始相机位姿偏差较小或较大时都能进行高精度图像匹配，同时具有较好实时性，如图6所示.

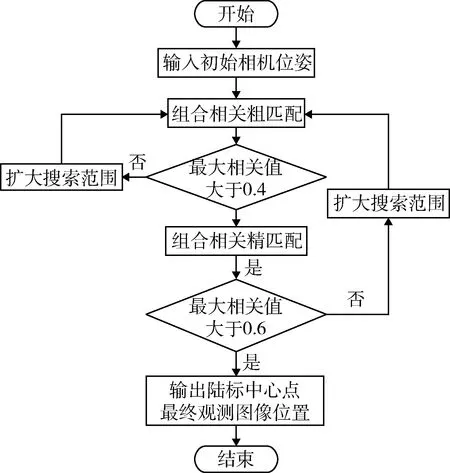
图6 组合相关匹配Fig.6 Combined correlation matching

首先，利用全局相关匹配进行粗匹配搜索，记下最大相关值对应的提取图像.对于粗匹配最大相关值设定一个阈值0.4，小于0.4表示图像弱相关和不相关，需要扩大搜索范围重新粗匹配；大于0.4表示中等相关和强相关就进行精匹配.如果粗匹配搜索范围大，可采取等间隔搜索，比如每隔5或10个像素进行搜索，减少运行时间.然后，针对粗匹配最大相关值对应提取图像，利用局部相关匹配进行精匹配，采用逐像素搜索.同样对精匹配最大相关值设定一个阈值0.6，小于0.6也需要扩大搜索范围重新粗匹配；大于0.6表示强相关和极强相关，达到精准匹配.最后，将两次匹配的偏移和作为最终偏移量，得到陆标中心点最终观测图像位置.

初始相机位姿偏差由初始提取图像与陆标真实观测图像的差异反映，相机位姿偏差越大，图像差异越大.距目标近距离时较大相机位姿偏差引起的图像差异可能很小，但远距离较小相机位姿偏差引起的图像差异可能很大.初始相机位姿偏差越大，粗匹配搜索范围越大，搜索间隔越大.当初始相机位姿小偏差时，粗匹配的搜索间隔可以减小为1.搜索间隔还与陆标大小有关，要保证相邻搜索具有较大重叠，至少大于1/2陆标尺寸.

1.4 位姿解算

利用预测图像与提取图像进行匹配，得到几个(大于3)陆标中心点的高精度图像位置和三维位置点对，即可采用PNP算法解算相机位姿.PNP算法通过多对3D-2D匹配点，利用最小化重投影误差来精确求解相机位姿.常见的PNP算法有直接线性变换(DLT)、P3P、EPNP、UPNP等.图像位置精度越高，3D-2D点对应越准确，相机位姿估计越准确.

2 仿真分析

运用Hayabusa大约7 km轨道拍摄的真实观测图像“st_2417397906_v_ddr”，结合实验室利用SPC生成的陆标数据作为输入.针对上述算法，对5个59×59的陆标进行了仿真测试.仿真条件：MATLAB R2018b，64位Windows 10，处理器为Intel (R) Core(TM) i7-8750H CPU @ 2.20 GHz 2.21 GHz.

给定相机一个较小偏差，将相机姿态按照ZYX方式分别旋转-1°、0.01°、-0.01°，同时将相机平移-55 m、87 m、0 m，三种相关匹配方法的最大相关值如表2所示，都大于0.6，没有明显差异.行误差、列误差定义为陆标中心点最终观测图像行、列坐标与真实行、列坐标差值，如图7、图8所示，除去个别值，行和列误差都在一个像素内.其他仿真结果如表3所示，三种匹配方法的均方根误差都达到亚像素精度，但实时性差异较大.根据最大相关值和均方根误差，三种匹配方法准确性差异不大.但根据运行时间，全局相关匹配实时性很差，组合相关匹配实时性较好，局部相关匹配实时性最好.

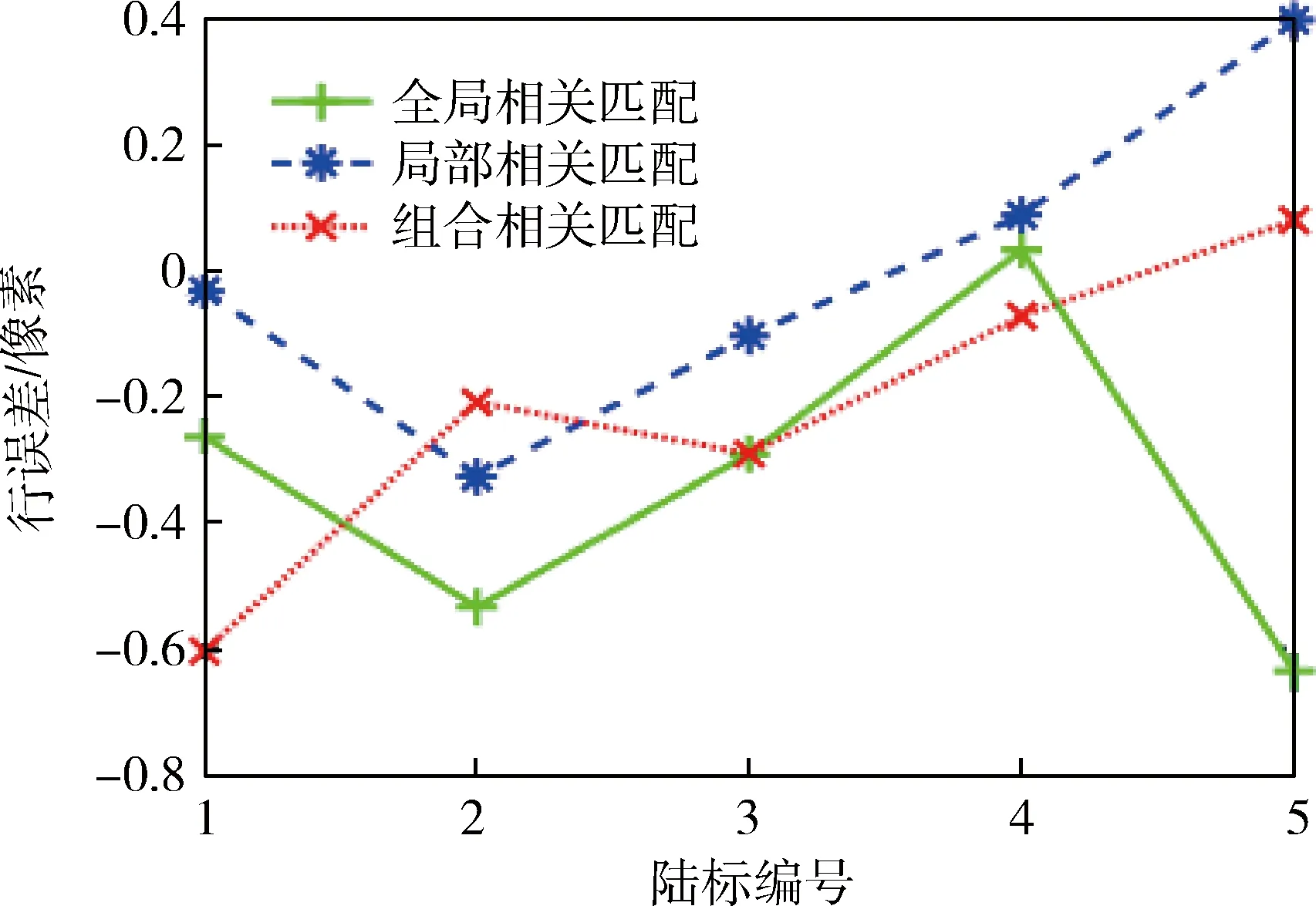
图7 较小偏差仿真行误差Fig.7 Row error of small deviation simulation

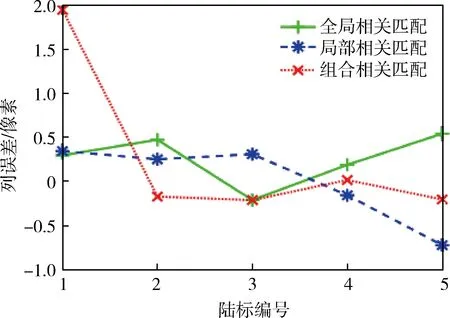
图8 较小偏差仿真列误差Fig.8 Column error of small deviation simulation

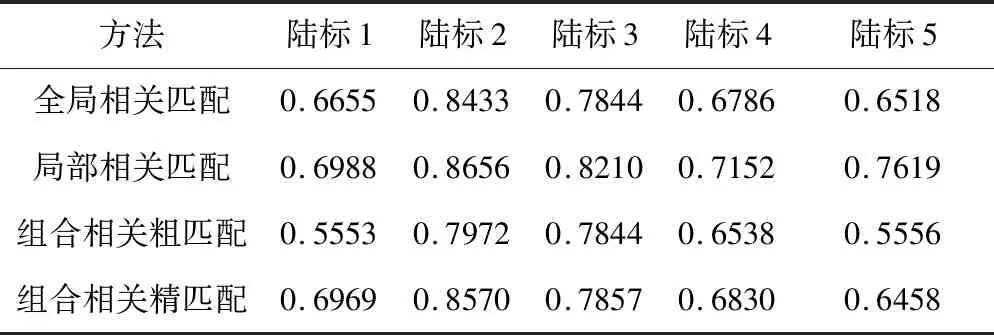
表2 较小偏差仿真最大相关值Tab.2 Maximum correlation value of small deviation simulation

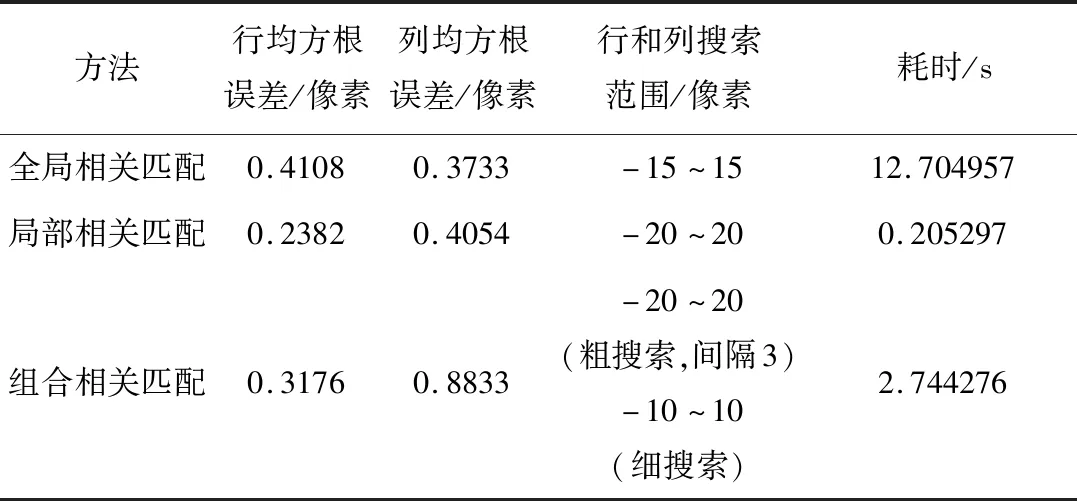
表3 较小偏差仿真结果Tab.3 Results of small deviation simulation

给定相机一个较大偏差，将相机姿态按照ZYX方式分别旋转-1°、0.2°、-0.2°，同时将相机平移-55 mm、87 mm、0 m，此时局部相关匹配方法失效，利用初始相机位姿生成陆标提取与预测图像差异过大，如图9所示.只能采用全局相关匹配或组合相关匹配方法，如图10所示，最大相关值如表4所示，两种方法差异不大.组合相关粗匹配最大相关值都大于0.4，精匹配都大于0.6.行误差、列误差分别由图11、图12所示，除去个别值，行和列误差都达到亚像素精度.其它仿真结果如表5所示，均方根误差都达到亚像素精度，但实时性差异巨大.组合相关匹配方法保证了准确性，又显著提高实时性.

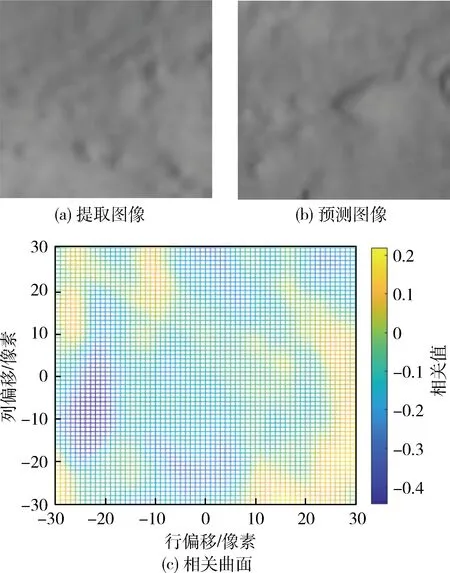
图9 局部相关匹配示意图Fig.9 Illustration of partial image cross-correlation matching

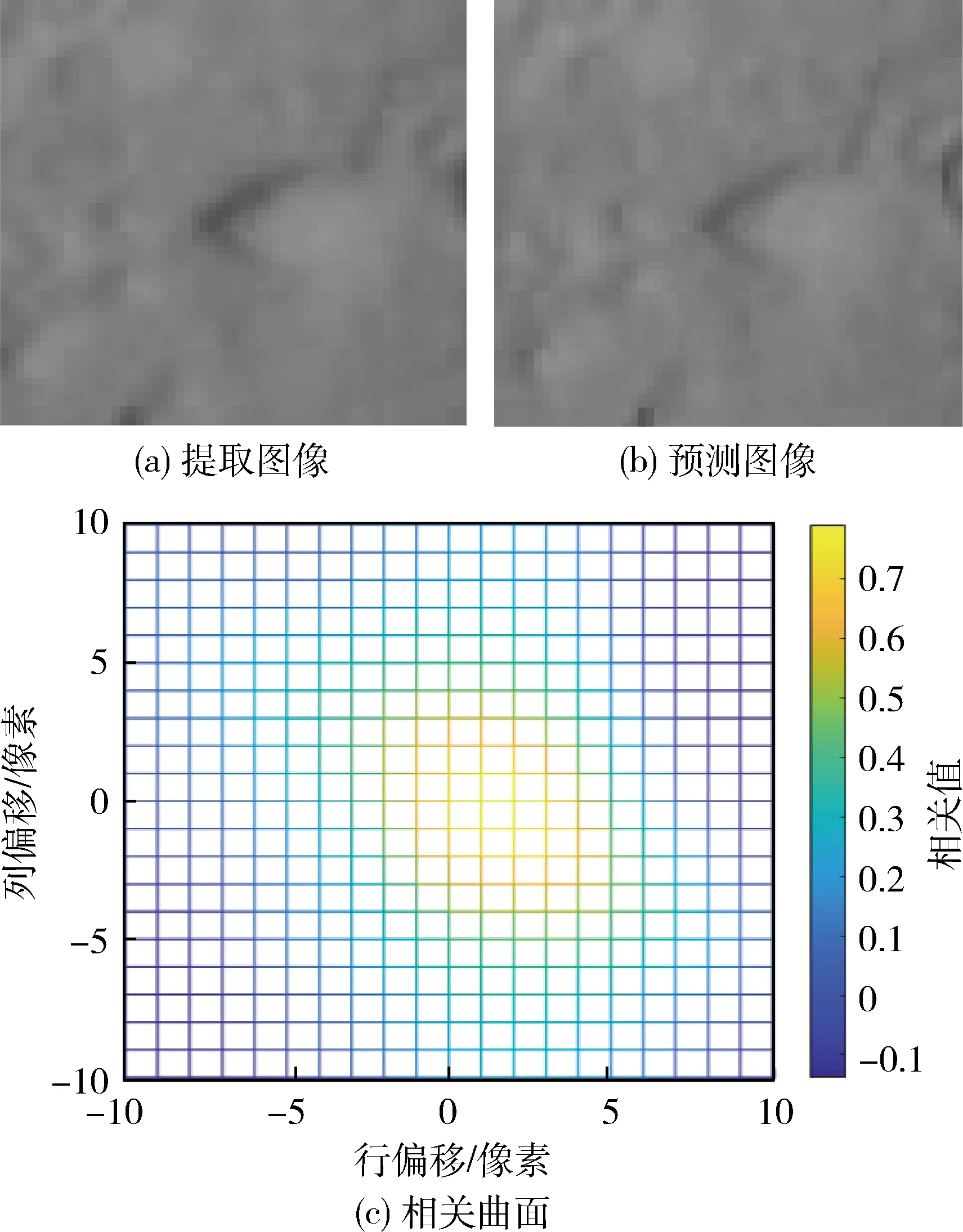
图10 组合相关精匹配示意图Fig.10 Illustration of combined correlation refined matching

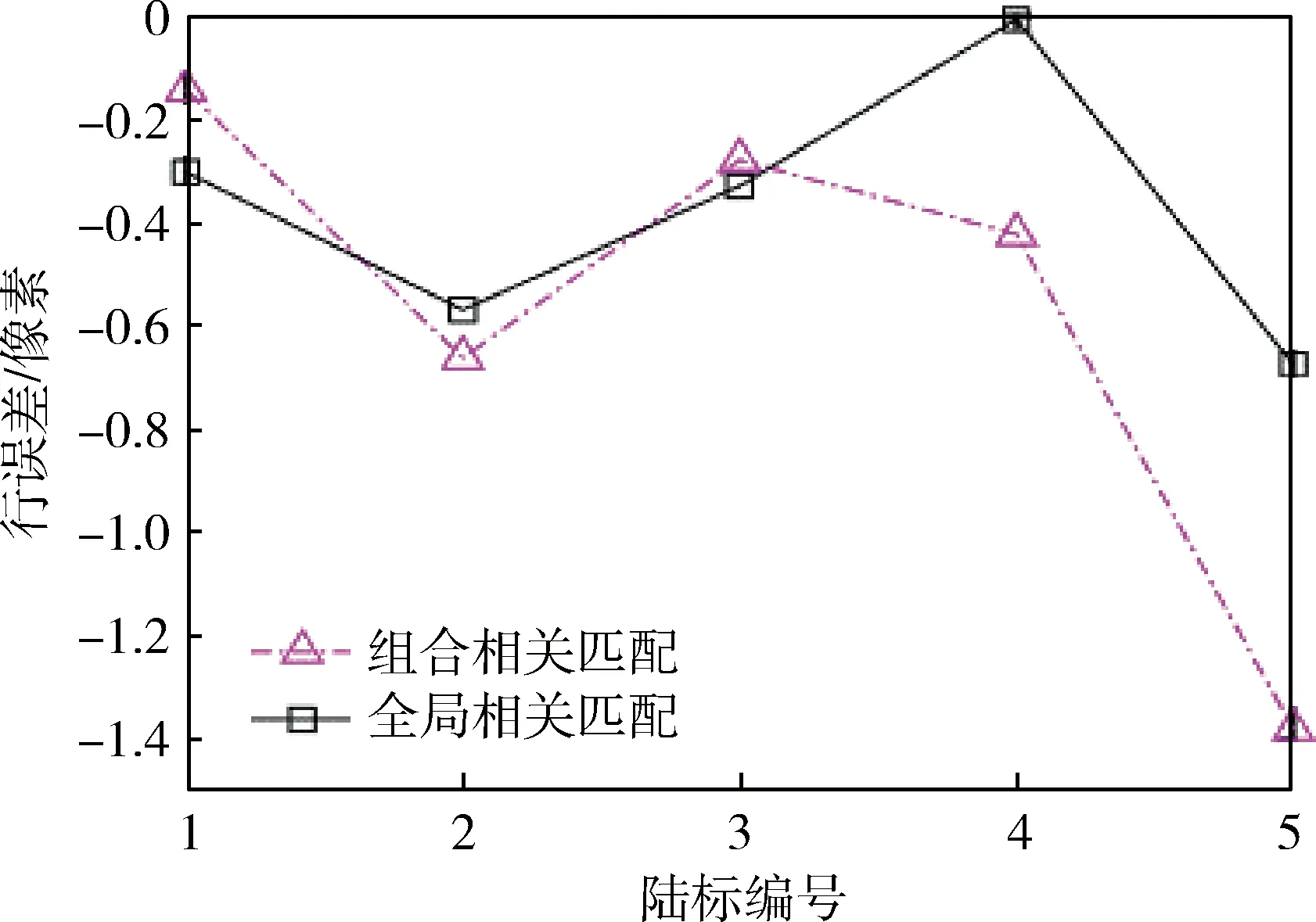
图11 较大偏差仿真行误差Fig.11 Row error of slightly large deviation simulation

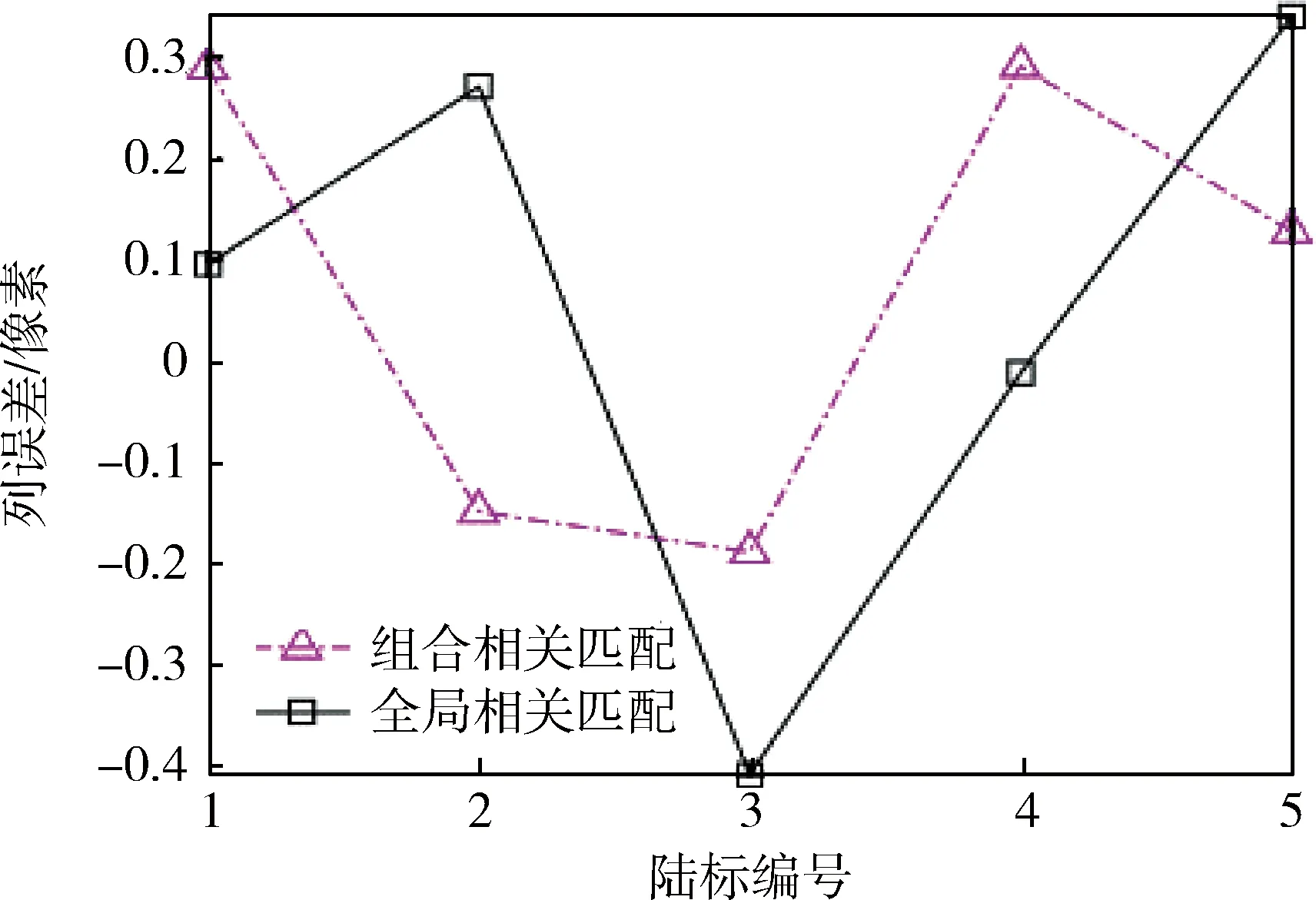
图12 较大偏差仿真列误差Fig.12 Column error of slightly large deviation simulation

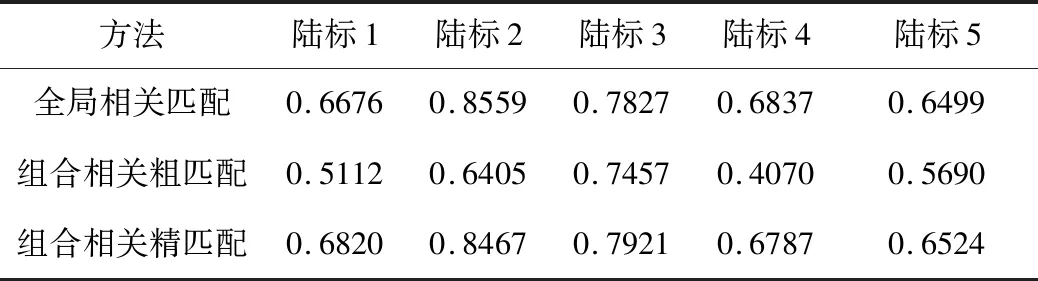
表4 较大偏差仿真最大相关值Tab.4 Maximum correlation value of slightly large deviation simulation

表5 较大偏差仿真结果Tab.5 Results of slightly large deviation simulation

目前已有基于SPC陆标的导航方法大多采用局部相关匹配方法，而本文所提陆标导航方法采用组合相关匹配方法.根据仿真结果显示，两者精度差异不大，都能够获取亚像素精度的陆标图像位置.而且本文导航方法在初始相机位姿偏差较大时同样得出精确解；并具有较好实时性，运行时间小于10 s，远小于全局相关匹配.

3 结 论

本文给出了一种基于SPC陆标的高精度相对导航方法.根据SPC光照模型直接渲染陆标的预测图像，并运用双线性插值生成陆标的提取图像，再使用组合相关匹配进行图像匹配，得到亚像素精度陆标中心点观测图像位置，即可利用PNP算法进行位姿估计.解决了在陆标与观测图像存在分辨率差异下的图像匹配问题，同时在初始相机位姿偏差较大时同样满足亚像素精度.但是初始相机位姿偏差很大时，该导航方法不适用，需要利用其它手段重新给出较为准确的初始相机位姿输入.通过仿真分析，所提方法能达到亚像素的图像位置确定精度，且实时性较好.后续工作一方面研究组合相关粗匹配的搜索范围、搜索间隔的具体选取依据.另一方面移植嵌入式，优化算法达到星载运行要求.