基于模糊强化学习的多柔性梁振动控制仿真
2021-04-25邱志成杜佳豪
邱志成,杜佳豪
华南理工大学机械与汽车工程学院,广东 广州 510641
0 引 言
随着科学技术的不断发展,人们对宇宙的探索不断进行着.仅在2018年,全球共执行114次发射任务[1].对航空航天器的功能要求使得航天结构大型化、复杂化、柔性化.航天航空器柔性结构在运动过程中容易产生残余振动,且频率低,时间长.结果,可能导致控制的性能下降.更糟糕的是各个柔性结构之间存在耦合关系.在最坏的情况下,可能会导致受控系统的不稳定[2],甚至造成疲劳损坏.
柔性梁粘贴压电传感器和致动器这种智能材料,也称智能结构,在主动振动抑制中的应用广泛[3].娄军强等[4]以压电陶瓷为致动器对旋转柔性机械臂系统进行振动抑制;GARCIA等[5]利用压电陶瓷贴片对柔性连杆机器人进行振动控制.多柔性梁振动存在耦合关系,非线性因素等,其主动控制是一个研究热点与难点.ABE等[6]提出了一种双柔性连杆点对点运动抑制残余振动的前馈控制方法;PRADHAN与SUBUDHI[7]提出一种新的非线性自适应模型预测控制器,用于双链柔性机械臂在不同载荷作用下的末端位置控制;ROSENZWEIG等[8]提出了一种基于预测水平向下采样的运动块法对末端弹性联接的多柔性梁结构进行振动抑制.
柔性梁的建模方法常见的有假设模态法、有限单元法等,利用Lagrange方程,结合变分法、虚功原理等方法进行建模[9].ANDREAS和THOMAS[10]使用Hamilton原理,对多柔性悬臂梁结构进行了建模;张娟等[11]对带有压电陶瓷作动器和传感器的平面智能柔性梁进行了有限元动力学建模.
近年来,强化学习控制得到了广泛关注.强化学习是机器学习的一个重要分支,其本质是描述和解决智能体在与环境的交互过程中学习策略以最大化回报或实现特定目标的问题[12].徐意钧等[13]提出一种基于概率推断式强化学习的关节控制方法以提高空间机械臂的自主操作能力.PRADHAN等[14]利用强化学习技术,对一个双连杆柔性机械臂的末端轨迹和振动进行实时自适应控制.
本文将研究多柔性梁耦合结构的残余振动,为此搭建多柔性梁耦合结构平台,采用有限元法,对该结构进行理论建模分析;设计了模糊强化学习控制器与PD控制器和自抗扰控制器,对多柔性梁的残余振动进行控制仿真,结果与PD控制器和自抗扰控制器进行比较.
1 多柔性梁结构有限元建模
为研究多柔性梁耦合结构特点,搭建了多柔性梁结构平台,以三柔性梁为例.为了给后续仿真提供环境模型,采用有限元法建立系统运动模型.
1.1 多梁耦合结构
如图1所示的为多梁耦合结构.隔振平台上安装有多柔性梁耦合结构.多柔性梁包括了3只柔性梁,一端固定,相邻两梁之间存在弹簧联接,最外边的柔性梁有弹簧与固定端联接.靠近自由端有激光位移传感器作为检测装置.
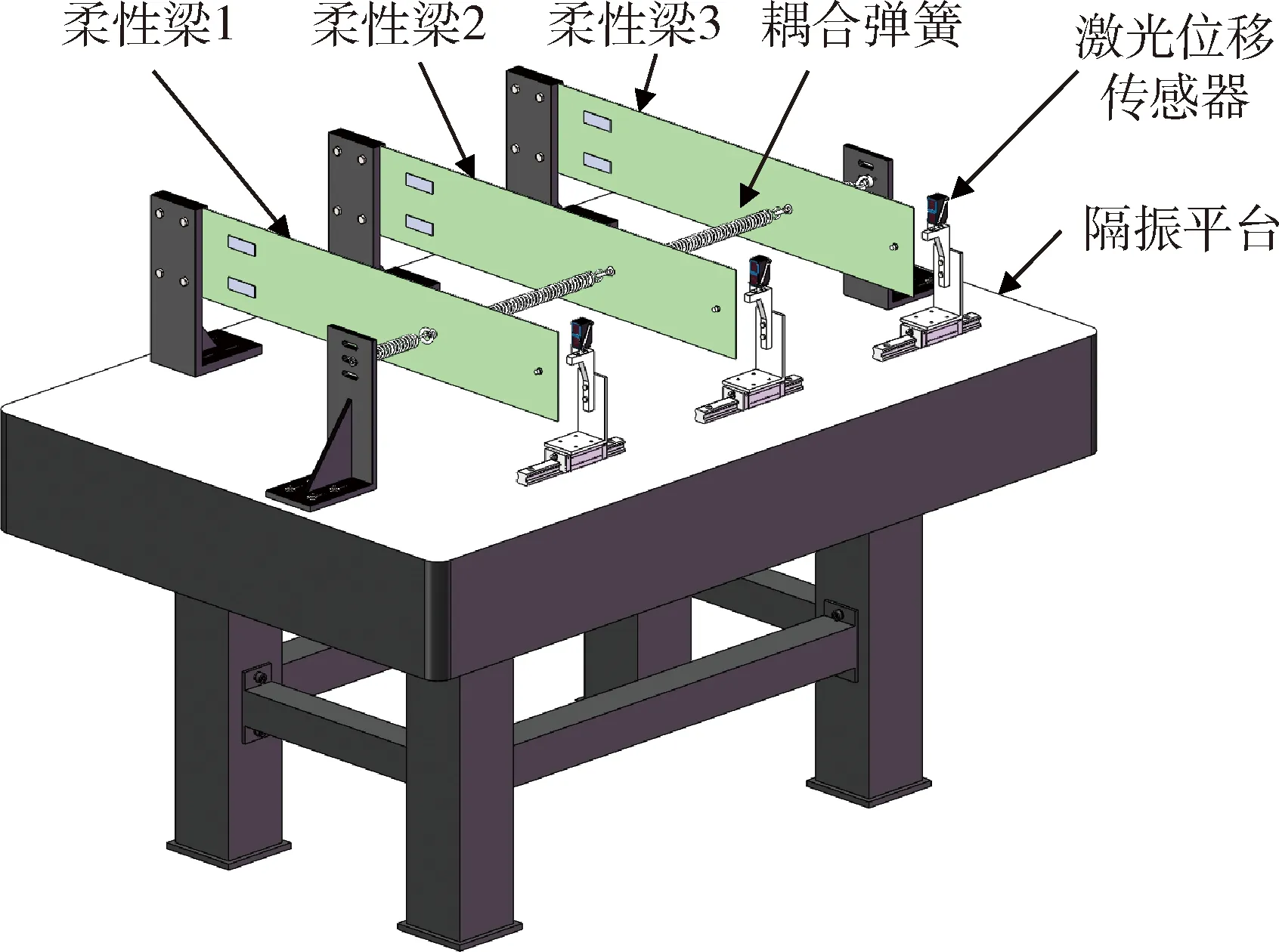
图1 多柔性梁结构Fig.1 Multiflexible beams structure
如图2所示为多柔性梁结构示意图.柔性梁靠近固定端粘贴有压电驱动器,双面对称粘贴,用于控制.一根梁上所有压电驱动器施加的电压相同.各梁接近末端添加有附加质量块.柔性梁使用环氧板制成,压电驱动器为压电陶瓷片.
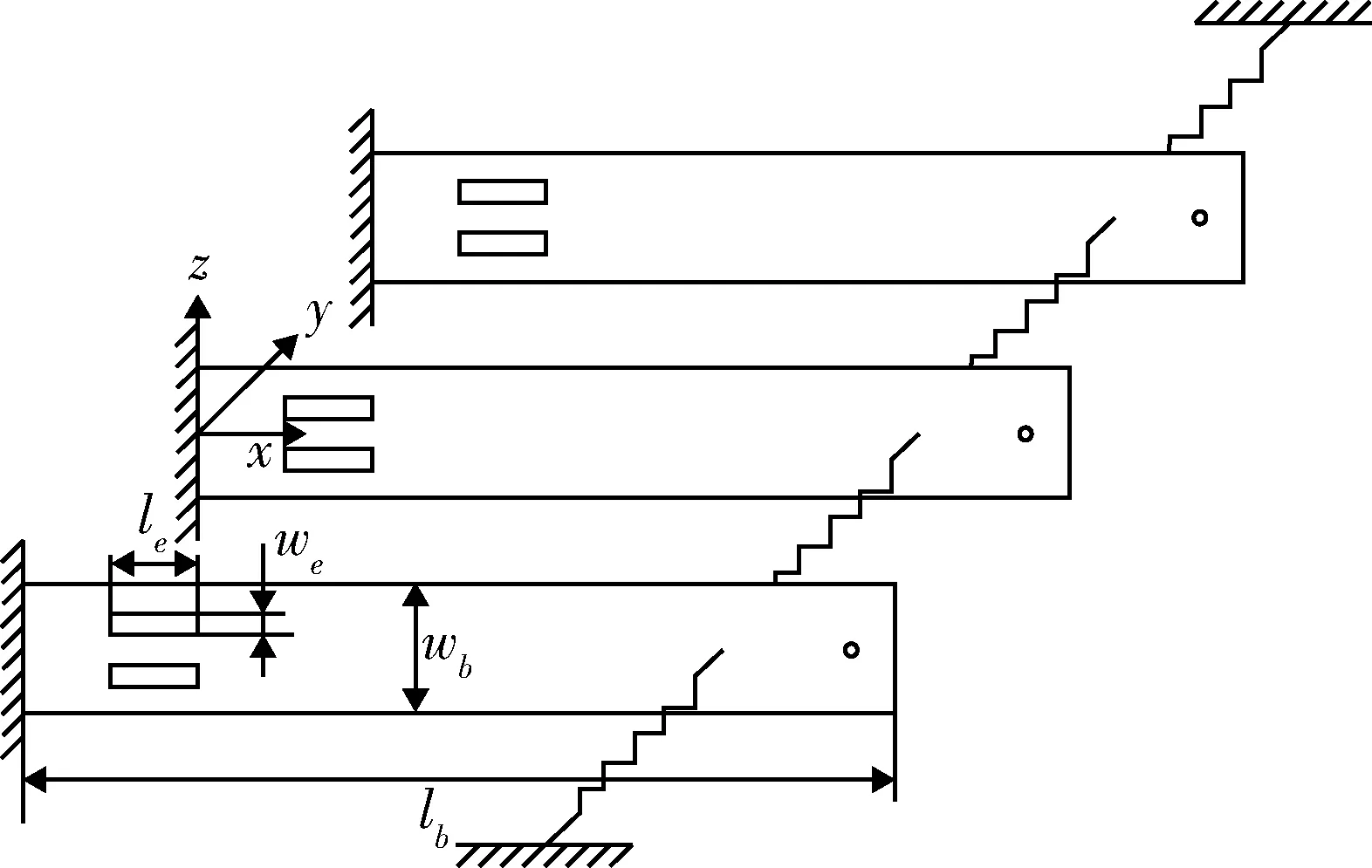
图2 多柔性梁结构示意图Fig.2 Schematic diagram of multi flexible beam structure
柔性梁的位置与激光位移传感器的位置均可在隔振平台上自由调整.弹簧刚度及附加质量块可以自由更换.
1.2 单元分析
如图3所示,为普通梁单元,图4所示为双面粘贴的压电梁单元,基于Euler-Bernoulli梁理论进行建模.
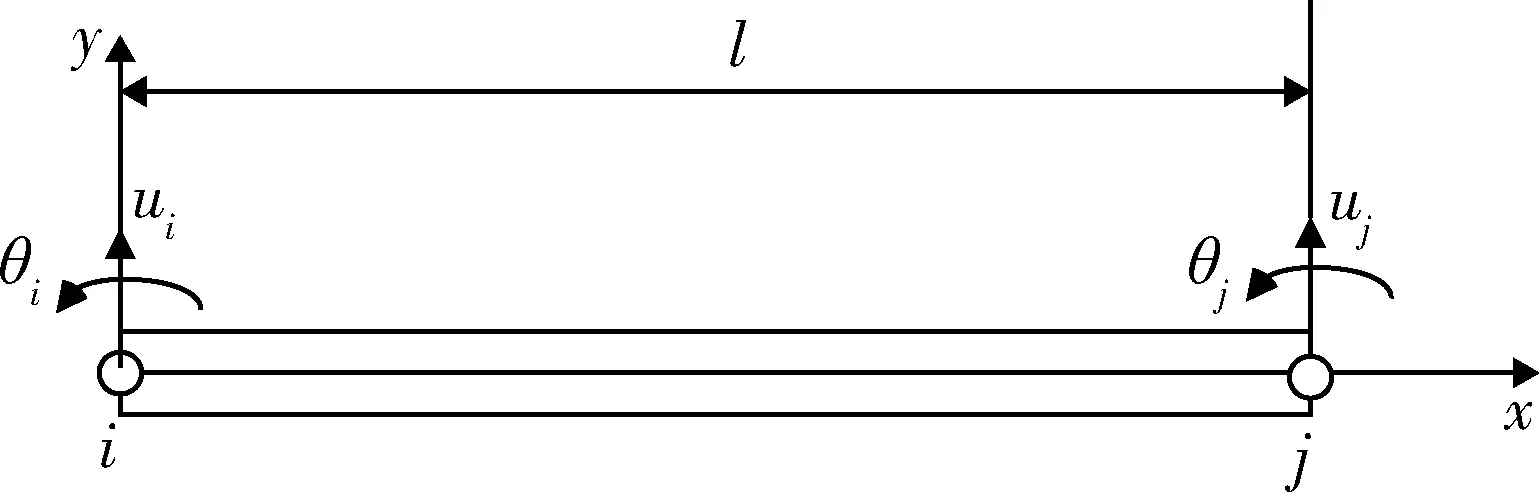
图3 梁单元示意图Fig.3 Schematic diagram of beam element
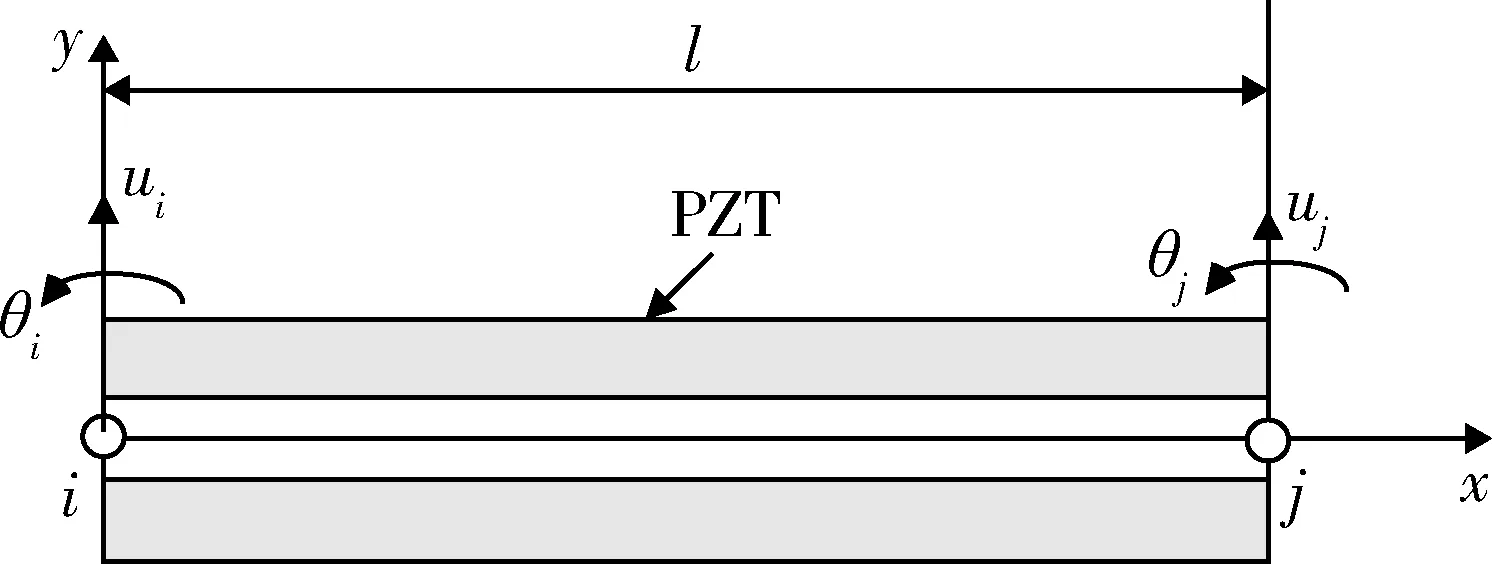
图4 压电梁单元示意图Fig.4 Schematic diagram of piezoelectric beam element
由Hamilton原理可知
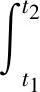
(1)
式中,L=T-U+Wf,T表示动能,U表示弹性应变能,Wf表示外力功[15].
(1)动能
普通柔性梁单元的动能为
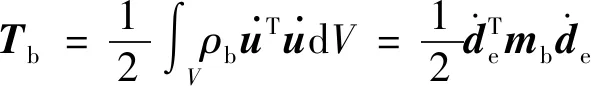
(2)
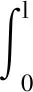
对于压电柔性梁单元的动能为
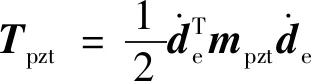
(3)

(2)应变能
普通柔性梁单元的应变能为
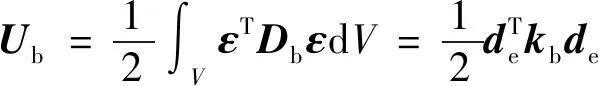
(4)
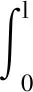
对于压电梁单元的应变能为
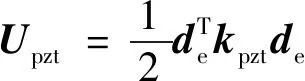
(5)
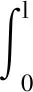
(3)外力功
设存在集中力fe作用于梁单元节点上,则普通柔性梁单元的外力功为
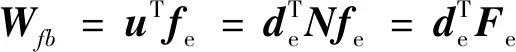
(6)
对于压电梁单元,则存在控制驱动力
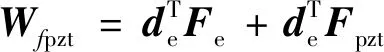
(7)
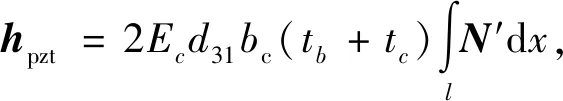
由式(1)可以得到两种单元的运动方程
此外,梁与梁之间的弹簧单元有
kspde=fsp
(8)
式中ksp表示弹簧的刚度矩阵.
最后是测量单元,采用的是激光位移传感器,其单元输出为
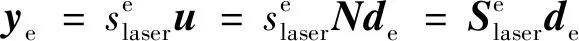
(9)
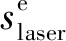
1.3 单元组装
将多柔性梁结构划分为有限数量的单元,如图5所示,将各个单元组装,并通过删除法添加固定约束,可以得到多柔性梁的总体运动方程
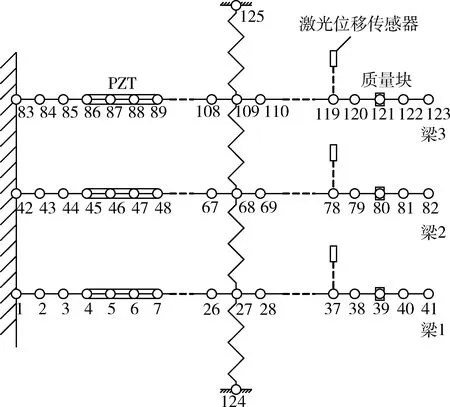
图5 单元节点示意图Fig.5 Schematic diagram of cell node

(10)
式中,M为总体质量矩阵,Λ=k0M+k1K为瑞利阻尼矩阵,其中k0、k1为质量阻尼系数和刚度阻尼系数;Fc=HcUc为压电驱动力矢量,Hc为总体的控制力系数矩阵,Uc为控制电压矢量,F为其他外力矢量,d为总体自由度矢量.
激光位移传感器输出可以表示为
Y=Slaserd
(11)
其中Slaser为总体测量系数矩阵.
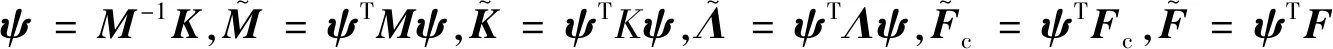
可以得到状态空间方程
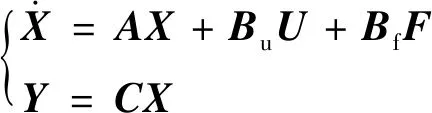
(12)

2 多柔性梁耦合结构特性
2.1 模态特征
所使用的材料以及结构尺寸如表1所示,弹簧刚度如表2所示,附加质量块均为0.05 kg.
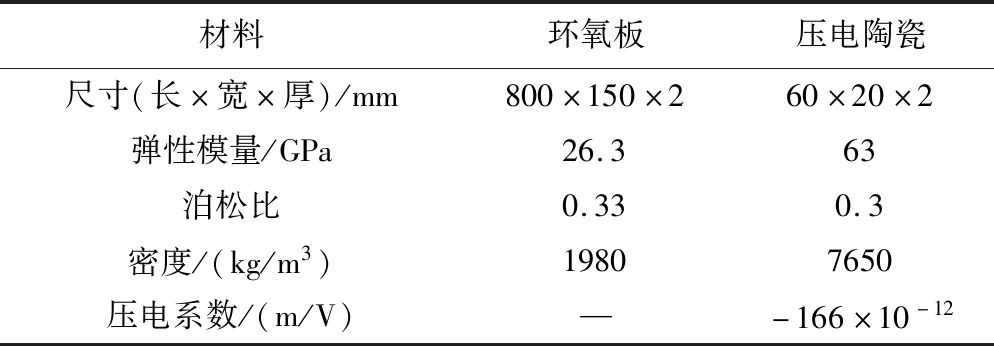
表1 材料属性Tab.1 The material properties

表2 弹簧刚度Tab.2 Spring stiffness
通过上述有限元建模方法,每个梁单元长度均为0.02 m,得到多柔性梁耦合结构的模态频率如表3所示,以及其对应的振型特征,如图6 (a)~(f)所示.可见前3阶模态频率较为接近,第4阶模态频率约为前几阶6倍,而之后的4到6阶频率又较为接近.多柔性梁耦合结构的残余振动呈现了密频的特性.
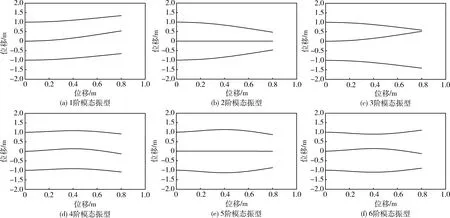
图6 各阶模态振型特征Fig.6 Modal characteristics of each order
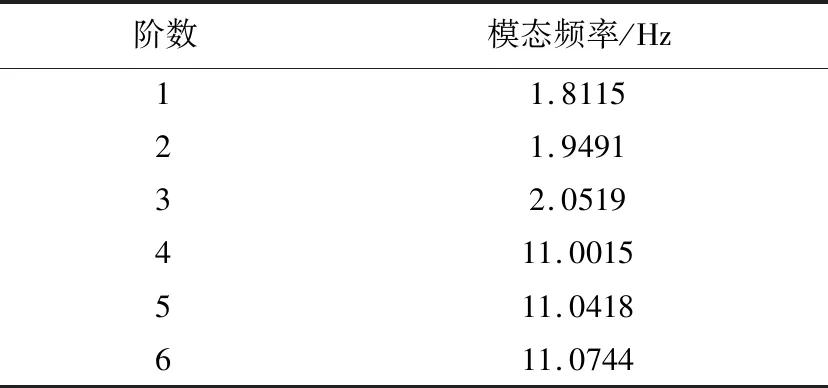
表3 模态频率Tab.3 Modal frequencies
2.2 模态截断模型
由于残余振动主要集中在前三阶模态中,为简化模型,仿真所采用的模型截取前三阶模态.不考虑施加的其他外力,仅考虑控制力作用,则式(12)的模态截断模型可以写成
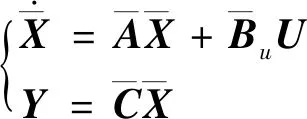
(13)
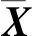
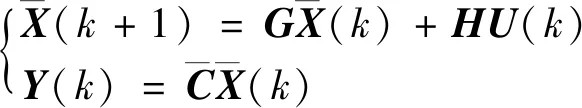
(14)
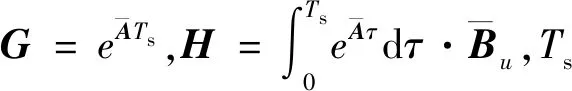
2.3 振动响应特性
如图7及图8所示,分别为激励1梁和激励2梁时所引起的响应,可见梁与梁之间存在着耦合关系,且有“此消彼长”的特点.
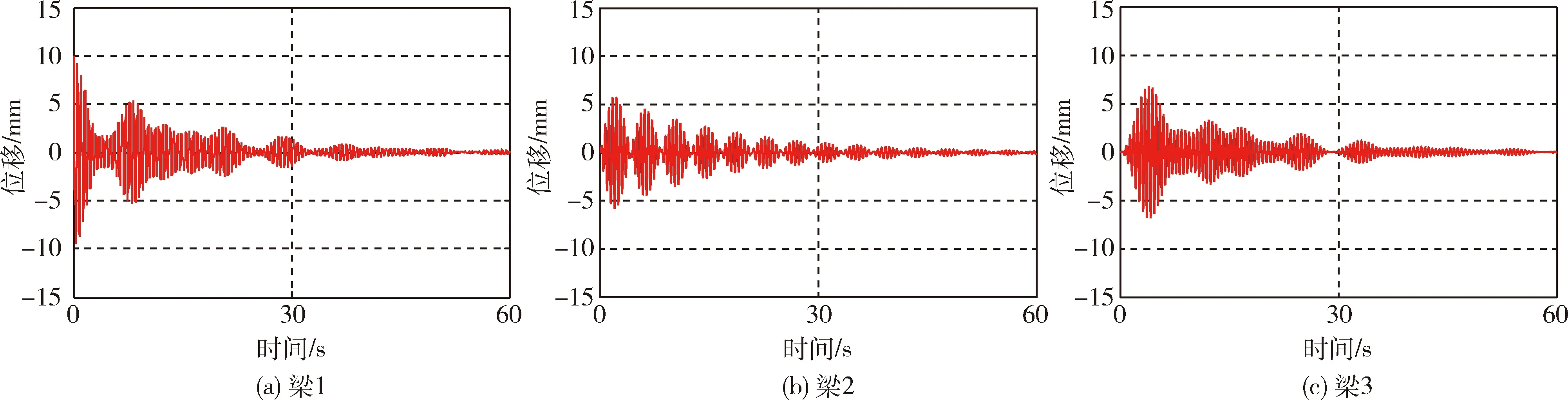
图7 激励梁1的振动响应Fig.7 Vibration responses of excitation beam 1
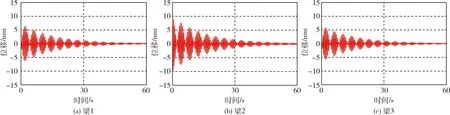
图8 激励梁2的振动响应Fig.8 Vibration responses of excitation beam 2
激励梁1时,梁1与梁3的振动主要为前三阶模态结合,梁2主要为1阶和3阶结合.三梁耦合呈现密频特性,拍频特征.而激励梁2时,三梁的振动均主要为1阶和3阶频率结合.三梁耦合也呈现密频特性,有很明显的拍频特征,且振动时间长,特别是小幅值振动.
3 控制器设计
3.1 自抗扰控制器
自抗扰控制由韩京清[16]提出,并在多个领域得到了应用.根据文献[17]设计多柔性梁结构自抗扰控制器如图9所示,其控制律为
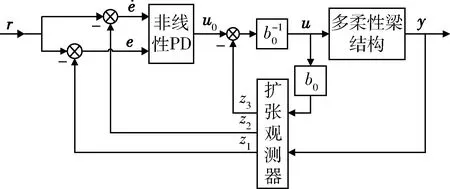
图9 自抗扰控制器控制框图Fig.9 Block diagram of active disturbance rejection controller
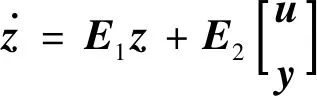
(15)
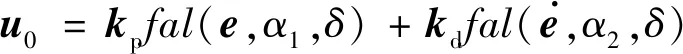
(16)
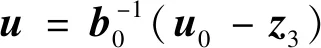
(17)
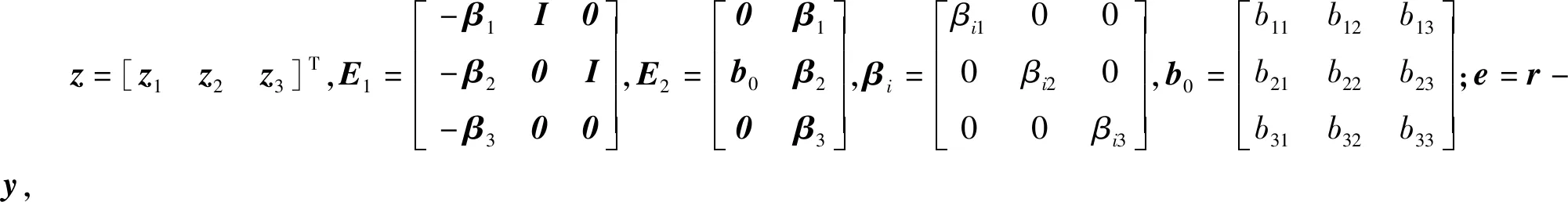
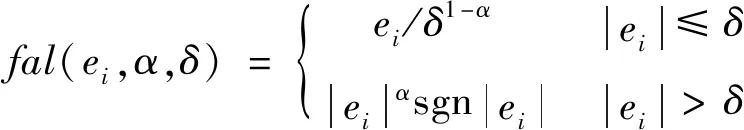
(18)
3.2 模糊强化学习控制器
强化学习在离散动作方面取得了许多成果,但难以处理连续动作方面问题,为此引入T-S模糊作为解决途径[18-19].
T-S模糊规则如下:
Ri:ifs1isFi1and...snisFin
thenui,1withqi,1or...ui,jwithqi,j.
式中,sm表示第m个状态,Fim为第i条规则相应的模糊集,m=1,2,…,n;ui,j为第i规则的后件第j个动作,qi,j为所对应的状态动作价值.由此可以建立模糊控制电压表{ui,j},以及动作价值表{qi,j}.
则对第i条规则有激活度
κi(s)=μ1(s1)×μ2(s2)…×μn(sn)
(19)
式中μm(sm)表示第m个状态隶属度.对激活度进行归一化操作有
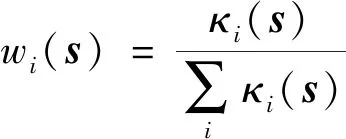
(20)
T-S模糊后件的选择通过ε-贪婪策略进行,即有1-ε的概率选择状态动作价值最大的动作,ε的概率选择其他动作,如下所示
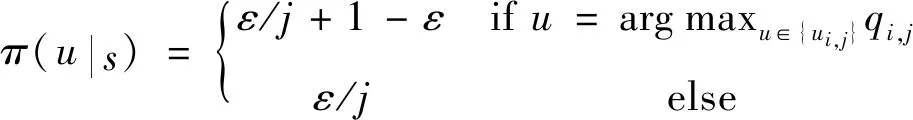
(21)
式中,π(u|s)表示在状态s下选择动作u的概率.
T-S模糊的实际输出为
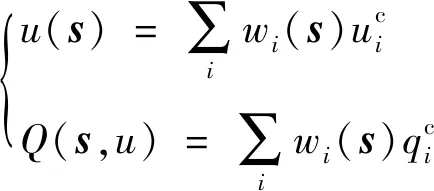
(22)
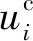
而强化学习目标为使得累计回报期望最大,即
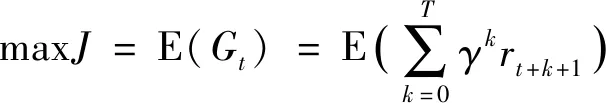
(23)
式中rt+1表示t时刻与环境互动后获得回报值,γ为折扣系数.而Q(s,u)反映当前状态s下采取控制电压u,所能获得的未来累计回报期望,即
Q(s,u)=E(Gt|st=s,ut=u)
因此,只要动作状态价值收敛,随着策略参数ε的减小,就能收敛到最优动作序列.
记动作状态价值的TD误差为
δt=rt+1+γQ(st+1,ut+1)-Q(st,ut)
对于每条规则后件的更新为
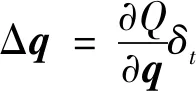
(24)
引入资格迹能有效加速训练效果[20]
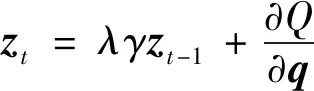
(25)
式中,λ为加权因子;zt为资格迹矢量,z0=0.则后件更新为
qt+1=qt+αδtzt
(26)
式中α表示更新步长.
对于多梁控制可以视为分别单独进行控制,对于模糊规则后件动作的设置,采用等差扩展的方法,即
式中,ui,mid表示所扩展动作的中项,nj与nmid分别为ui,j与ui,mid的对应项数,di为公差.
回报设置为
r=-sTKs-uTΓu
(27)
式中K与Γ分别为状态权重与电压权重.
如图10所示,为模糊强化学习控制框图.图11为控制流程图.
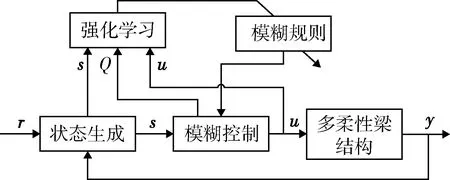
图10 模糊强化学习控制框图Fig.10 Fuzzy reinforcement learning control block diagram
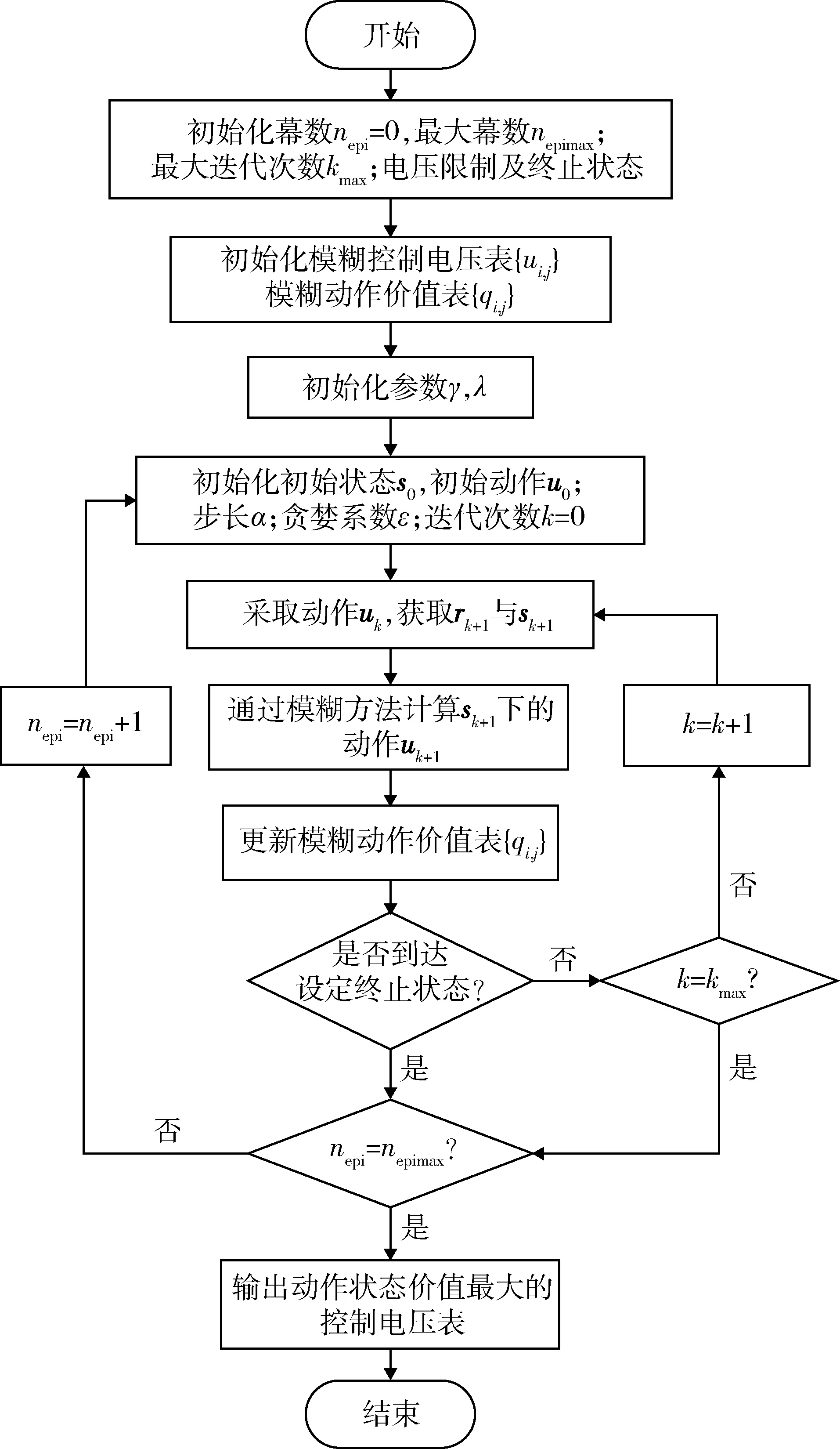
图11 模糊强化学习控流程图Fig.11 Flow chart of fuzzy reinforcement learning control
4 数值仿真
4.1 PD控制器仿真
PD控制器控制律如下所示:
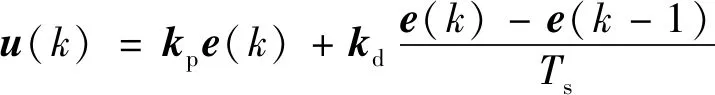
(28)
式中,e(k)=r(k)-y(k),r(k)表示参考值,u(k)为控制输入,kp,kd分别为比例项增益系数矩阵和微分项增益系数矩阵.
在MATLAB中进行仿真,以激励梁1为例,设置梁1初始位移为10 mm,振动1 s后控制介入;控制电压u∈[-150,150]V.
PD参数选择为比例kp=diag{23,23,23},微分kd=-diag{1.5,1.5,1.5}.如图12所示为PD控制各梁的振动情况;如图13所示为各梁控制电压图.可以看出PD控制大幅值振动衰减迅速,但是小幅值的振动持续时间较长.
图12 PD控制下各梁振动Fig.12 Vibration of each beam under PD control
图13 PD控制下各梁控制电压Fig.13 Voltage of each beam under PD control
4.2 自抗扰控制器仿真
在MATLAB中进行仿真,以激励梁1为例,设置梁1初始位移为10 mm,振动1 s后控制介入;控制电压u∈[-150,150]V.

如图14所示为自抗扰控制器各梁的振动情况;如图15所示为各梁控制电压图.自抗扰控制器控制效果略优于PD,但其结构也更为复杂.
图14 自抗扰控制下各梁振动Fig.14 Vibration of each beam under ADRC control
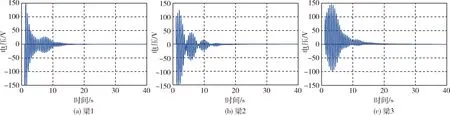
图15 自抗扰控制下各梁控制电压Fig.15 Voltage of each beam under ADRC control
4.3 模糊强化学习控制器仿真
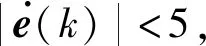
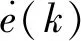
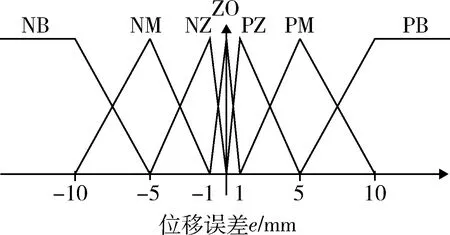
图16 位移误差模糊集Fig.16 Displacement error fuzzy sets
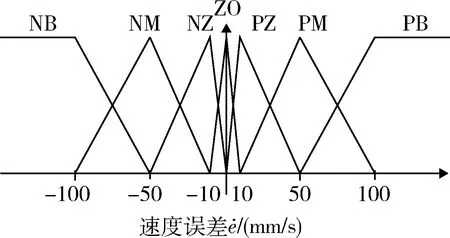
图17 速度误差模糊集Fig.17 Speed error fuzzy sets
设置折扣系数γ=0.99,加权因子λ=0.6.贪婪系数ε随着幕数nepi变化为ε=0.5×0.99nepi,步长α也随幕数nepi变化,α=0.8×0.99nepi.
如图18所示为第1次训练的控制效果与第500次训练控制效果对比;图19所示为第1次训练的控制电压与第500次训练控制电压对比.可以看出,第1次训练中的控制电压较为紊乱,控制几乎无效果,而在第500次训练时,控制效果得到很明显的提升.
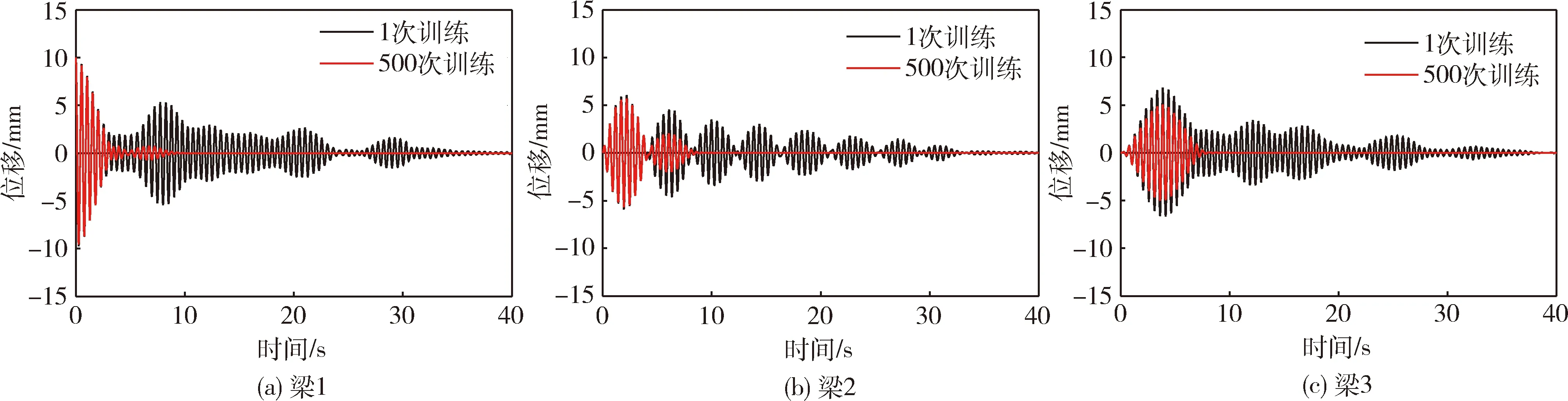
图18 模糊强化学习控制下各梁振动Fig.18 Vibration of each beam under FRLC
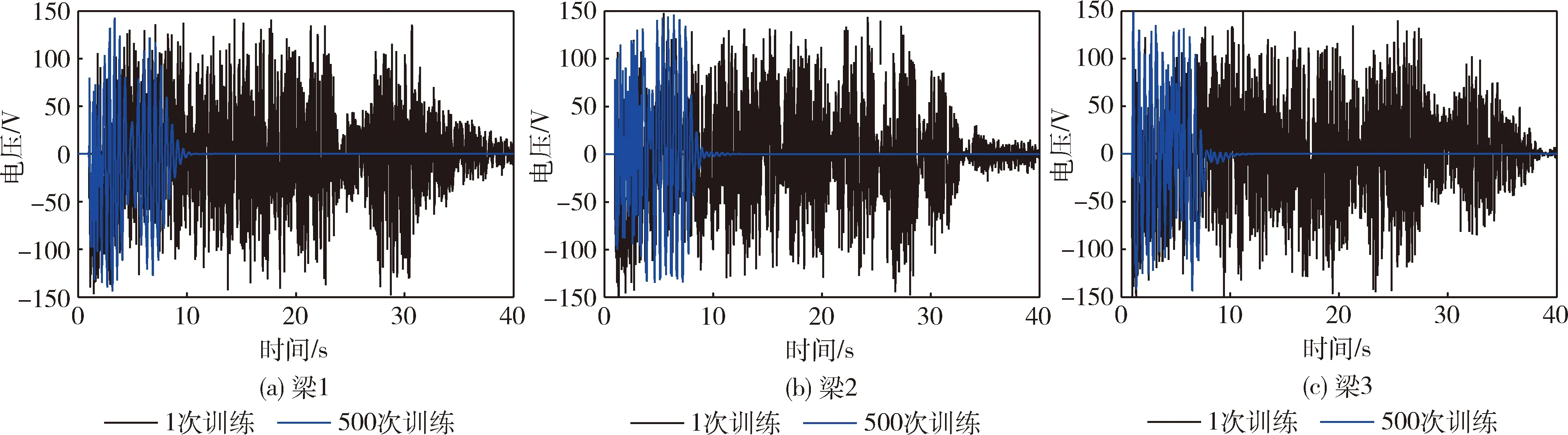
图19 模糊强化学习控制下各梁控制电压Fig.19 Voltage of each beam under FRLC
为了解决训练开始控制电压大范围跳动可能造成对压电片的损伤,且初期几乎无控制效果的问题,鉴于模糊控制表具有很好的可移植性,使用PD控制电压初始化设置扩展动作的中项umid,公差d=5 V,扩展数量为21.其控制效果如图20与图21所示.可见训练开始时的效果接近于PD控制效果,经500次训练后控制效果有明显提升.
图20 PD初始化模糊强化学习控制各梁振动Fig.20 Vibration of each beam under FRLC with PD initiated
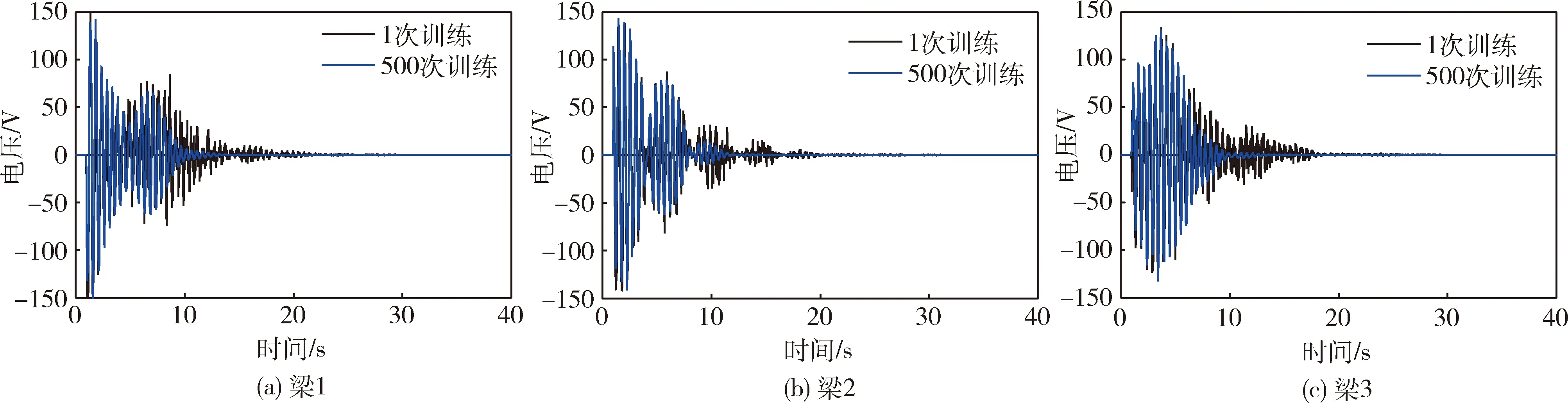
图21 PD初始化模糊强化学习下的各梁控制电压Fig.21 Voltage of each beam under FRLC with PD initiated
图22显示每幕到达设定终止状态时所经历的时间.虽然到达终止状态时间存在一定的变动,但总体趋势可以明显看出,随着幕数增加,到达终止状态的时间越来越短,然后逐渐趋平.
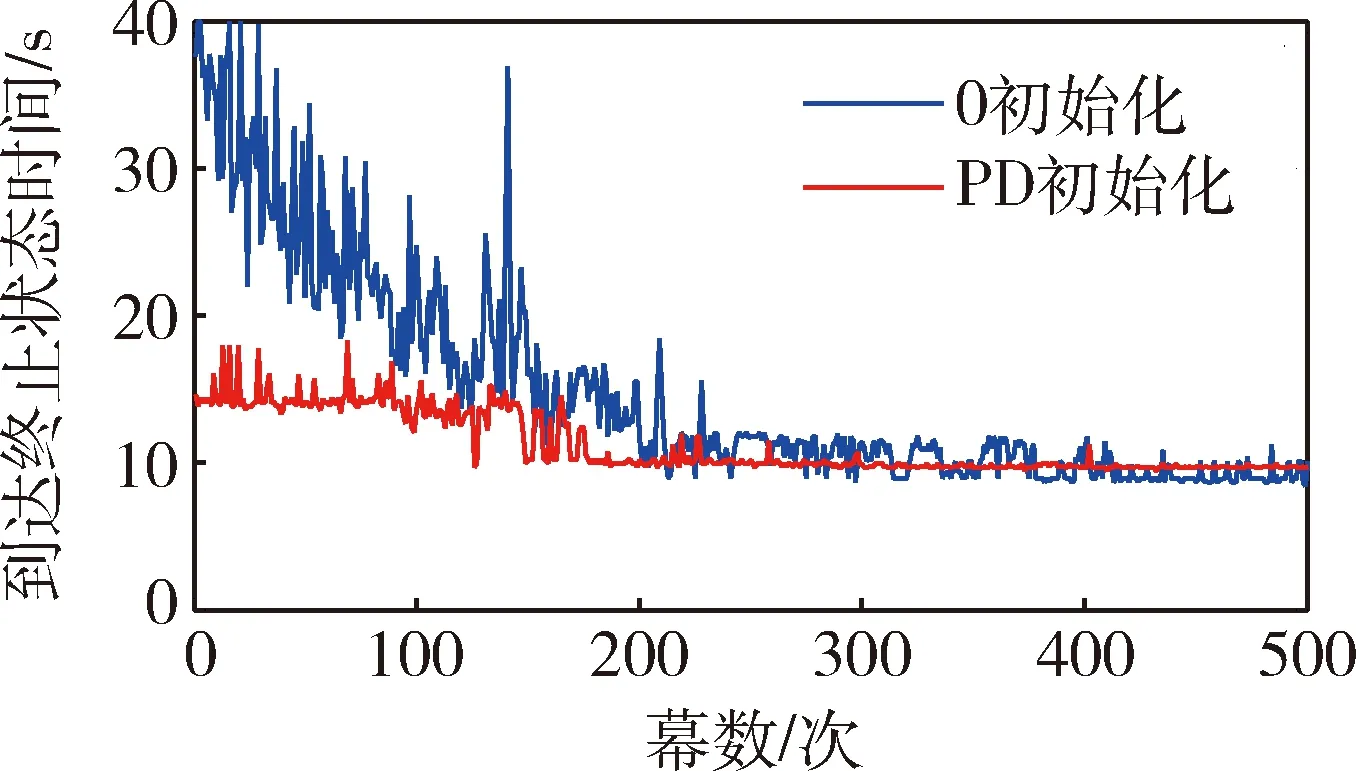
图22 训练过程Fig.22 Training process
相比于自抗扰与PD控制器,模糊强化学习控制能够更好的抑制小幅值振动.自抗扰控制器到达终止状态时间需要13.5 s左右,而经过500次训练的模糊强化学习控制器到达终止状态仅需要10 s左右.
5 结 论
针对多柔性梁残余振动的主动控制,本文分析了残余振动密频的特点,设计了模糊强化学习控制器,并进行训练及控制的仿真,采用PD初始化控制电压表能在初期得到较好效果.结果显示模糊强化学习控制器能有效地控制多梁残余振动,特别是小幅值的振动.
