鲸豚表皮微尺度柔性变形的减阻原理研究

黄苗苗，张 楠，卜淑霞，朱爱军，张 华

（中国船舶科学研究中心水动力学重点实验室，江苏无锡214082）

0 引 言

无论对于水面舰船还是水下航行体，快速性一直都是综合航行性能的关键组成部分之一。经过长期的研究和发展，通过线型优化降低阻力的空间和幅度越来越小，进一步的减阻必须借助于新型减阻技术。海洋鱼类体表结构经过亿万年的自然优化选择，进化形成了许多特异结构和优异减阻功能，具有非凡的低阻高效游动能力。仿生减阻研究的重要启示首先来自于对海豚的研究[1-2]。1936年，英国生物学家James Gray[1]基于海豚快速游动现象提出了著名的格雷悖论，从而引发了之后几十年对海洋高速鱼类仿生减阻研究的热潮[3-7]。

国外在上世纪六十年代就开展了仿生柔性面的减阻研究，包括实验及数值计算方法研究[8-11]。我国从上世纪末开始柔性面的理论和试验研究，如中国船舶科学研究中心的张效慈[12]开展了柔性面减阻降噪的理论分析；黄微波等[13]采用CFD 模拟研究了定常随行波作用下的涡街形式。整体来看，与国外相比我国在仿生柔性面减阻方面的研究较少，特别是数值计算方面有待深入研究。

Carpenter 等[14]在研究海豚皮肤时发现：海豚表皮光滑，在皮肤表面下隐藏着一些纤维结节，当海豚游动时，随着滑过海豚体表的水流剪切力的增大，海豚皮肤逐渐由光滑转变成具有一定几何形状的非光滑形态，从而实现减阻目的。也就是说，活体海豚皮肤的柔性是自主依靠肌肉上下垂直抖动形成表面有规律的动态起伏。而这方面的研究比较欠缺，因此，本文开展了鲸豚表皮微尺度柔性变形的非定常数值计算研究。

1 生物观测

在柔性面计算参数的选取时，本文参考了国外文献中的海豚表皮观测结果。虽然用肉眼观察比较模糊，但是在很多齿鲸（如海豚）的皮肤表面确实分布着波纹状的规则沟嵴。这些沟嵴较浅，在海豚死后会因为皮肤松弛而模糊或消失不见，同时很难在皮肤的组织切片中观察到，文献中采用快速固化方法对活体齿鲸亚目动物的皮肤嵴进行了压印和测量[15]。

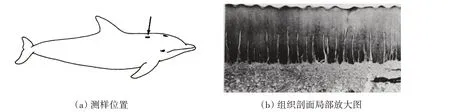
图1 海豚背部皮肤嵴[15]Fig.1 Surface cutaneous ridges on the dorsal thorax of a dolphin[15]

由于这种皮肤嵴的尺寸很小，都是微米（μm）量级，观测活体鲸豚尚需使其处于安静状态，并借助于特别的处理方法。对于研究仿生减阻的人，我们关心的是这种皮肤嵴在鲸豚高速游动过程中是如何变化发挥作用的，抑或是不动即可减阻？本来通过实时观测就能直接回答这个问题，但是目前的测试水平尚达不到，因此本文开展了这方面的数值研究工作来进行探索。

2 计算方法

文中采用计算效率高，预报精度也能满足工程实用的RANS 方法对柔性表皮开展阻力流场的数值模拟，数学控制方程包括连续性方程和Reynolds方程[16]，湍流模型采用k-ε模型。

文中数值计算涉及的柔性变形依靠动网格技术实现。对于动网格，在任意一控制体∂V（边界是运动的）上，标量ϕ积分形式的守恒方程为

守恒方程中的时间导数项采用一阶后向差分格式写作

图2 是本文计算模型，顶部为刚性无变形的平板固壁，底部为柔性面，两者为平行状态。左侧设为水流入口，右侧设为出口，计算中出入口均设为周期性边界条件。计算域底部边长记为L，计算域大小为L×L×5L，顶、底部距离Δz=5L，以防止顶部固壁边界层影响下层流场。本文计算模型采用结构化网格，网格总数为400万。

图2 计算域及柔性面上的网格分布Fig.2 Computational domain and mesh pattern for compliant surface

本文选用刚性波来代替海豚可能不变形的波状规则沟嵴，用驻波和流向随行波来代替海豚皮肤可能的柔性变形，尚不考虑其表面的弹性影响。

刚性波面表达式为

驻波柔性面表达式为

流向随行波柔性面表达式为

3 模拟结果

为了探寻可能的仿生减阻方案，本文对刚性的及柔性的波状壁面进行了阻力数值模拟，作为对比，同步计算了刚性平板。计算工况Re范围为106～107。

3.1 计算精度检验

3.1.1 与实验结果比较

本文计算方法与试验结果给出的平板壁面无量纲速度分布曲线如图3 所示，图中圆点为Abra⁃ham的经典实验结果[17]，实线为本文数值计算结果，两者总体吻合良好。

3.1.2 与经典拟合公式比较

采用Schlichting 平板湍流边界层壁面局部摩擦系数近似公式（7）[18-19]，计算本文刚性平板局部摩擦系数，并与数值模拟结果对比。如表1所示，两者差异基本在1%之内，说明本文的数值计算方法是可行的。

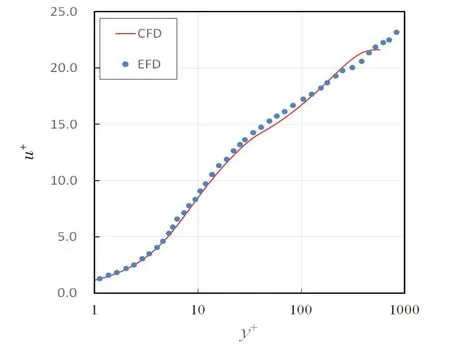
图3 平板壁面无量纲速度试验对比Fig.3 Comparison of dimensionless velocity on plate between the simulation and experiment results

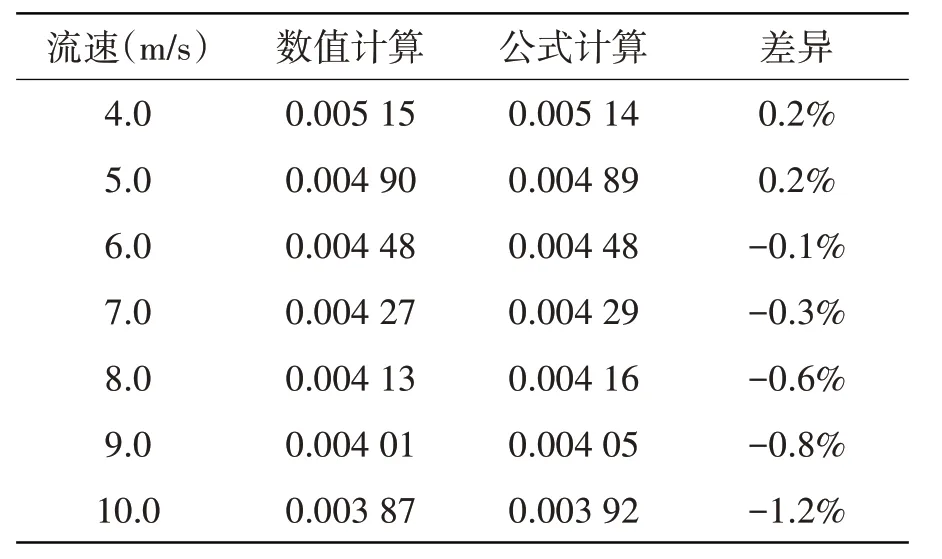
表1 平板摩擦阻力系数对比结果Tab.1 Comparison of plate friction coefficients

3.2 流场分析

针对不同壁面表达式（4）～（6），选取入口速度5 m/s时的流场开展对比分析。下文中涉及的流向剖面为本文计算域中y=0.5L处的xz平面，如图4所示。

3.2.1 刚性波面ζ = acoskx

图5给出了对应的速度云图。右向流动的边界层内，由波峰→波谷→波峰形成的壁面凹陷，产生了流道周期性收缩扩散区，对应了近壁面流场的高速与低速区。故速度等值线呈波状分布，且与波面基本上呈反相。其中波谷→波峰面为迎流物面，它的压力显然应该高于相邻波峰→波谷的背流面。于是产生流向的压差阻力，这是平板绕流不存在的。

图4 流向剖面示意图Fig.4 Streamwise section

图5 刚性波面流向剖面速度云图Fig.5 Velocity magnitude of rigid wave surface

图6 则是这一凹陷区的速度矢量图。对于右向流动，它清楚显示了顺时针旋转的驻涡存在。这一驻涡将使凹陷区相当部分壁面速度梯度比平板小，甚至梯度变负。这样，即使在波峰处，速度梯度高于平板，但其总粘性阻力将比平板低。由于顺时针驻涡的存在，流向最大流速不在刚性波面的波谷处，而是在波谷稍后的下游处，所以速度波状等值线的“谷”仍然对应壁面波峰处，而“峰”则对应壁面波谷稍后的下游处。

图6 刚性波面近壁区速度矢量图Fig.6 Velocity vector of rigid wave surface

图7 驻波柔性面流向剖面速度场云图Fig.7 Velocity magnitude of active compliant surface with standing waveform

3.2.2 驻波波面ζ = acoskxcosωt

图7 为稳定计算结果中选取的一个周期内速度云图。自t=0 时刻（图7（a））起：节点A、B 之间波面从波峰降至平面（t=T/4），再降至波谷（T/2），一直在让出流道空间，对应z 向便存在较大低速影响区；而此时相邻的节点BC 波面自波谷至平面（T/4），再至波峰（T/2），不断压缩流道空间，从而z向为较小的高速影响区。故其速度等值波状线与运动的驻波面反相。

虽然波峰、波谷不断在交替变化，但造成壁面高低不平必然会产生压差阻力。若驻波最大波高与刚性波一致，在t＞0 时驻波壁面的高低不平程度低于刚性波壁面，可以预期对应的压差阻力将比刚性波小。

图8 给出了驻波面的峰→谷→峰凹陷区，同样存在顺时针旋转的驻涡，这意味着其摩擦阻力应低于平板。

3.2.3 流向随行波ζ = acos( kx - ωt)

对于随行波壁面上任意两个质点，它们对应的z向无穷远处均为来流u，而它们自身仅在z向上下运动，规律完全一样，只差相位。这就注定了边界层流场的速度等值线，应该有随行波面类似形状，并且是同相的。图9的速度云图证实了这种分析。

在大地坐标系中观察波峰→波谷→波峰形成的凹陷区。对于刚性波面，位置、大小都是不变的；对于驻波面，位置不变，波高呈周期性正负变化。虽然随行波以波形的波速c=流向移动，但波面质点x位置固定不变。只是位于“波峰→波谷”波面上的质点总是以有规律的正z向速度驱赶流体，使“峰→谷”波面以流向速度c挤压凹陷区中的流体空间，而凹陷区中的“谷→峰”波面上质点以一定规律沿负z向速度运动，使谷→峰波面以流向速度c让出空间，接纳上游被驱赶来的流体，如图10速度矢量所示。

图8 驻波柔性面近壁区速度矢量图Fig.8 Velocity vector of active compliant surface with standing waveform

图9 随行波柔性面流向剖面速度场云图Fig.9 Velocity magnitude of active compliant surface with traveling waveform

这一物理过程表明，随着流向波速由零（刚性波面）开始增加，“谷→峰”波面将由第3.2.1 节中迎流面角色转变为不断让出流场空间的角色，压力分布由高变低；而“峰→谷”波面由第3.2.1 节中背流面角色转变为不断驱赶、挤压流体向下游的角色，压力分布由低变高。从而使压差阻力由刚性波面的值不断减小，乃至变为推力。

这一物理过程同时表明，流向波速由零增加，意味着凹陷区中近壁面流向速度增加，并逐渐减弱原刚性波面凹陷区中的驻涡强度。只要波速足够大，驻涡强度会低于驻波、刚性波，乃至消失，并不断使壁面正向速度呈梯度增加。所以可预计到摩擦阻力将不断增加。

图10 随行波柔性面近壁区速度矢量图Fig.10 Velocity vector of active compliant surface with traveling waveform

3.3 阻力的数值预报

对文中四种面板开展阻力模拟对比，涉及的无量纲参数如下：

式中，δv为壁面粘性单位，λ为柔性面波动的波长，a为柔性面波动的波幅，T为波动周期，u为流速，c+为随行波无量纲行波波速。

式中，Ft为总阻力，Fp为其中压力积分值，Fτ为其中的剪切应力积分值，s为面板表面积。结果处理中柔性面与平板均取实际面积，驻波形式的柔性面面积做周期变化，因此取最大与最小波幅的面积平均值。受力分析均采用计算稳定后的结果，其中流向随行波及驻波柔性面均选取计算稳定后两个周期内的时历监测值作为最终计算取值。

为了便于比较，表2～4中所有算例的波陡全部一样。

3.3.1 刚性波面ζ = acoskx

从表2可以看出，刚性波面摩擦阻力系数Cτ如同平板一样，随来流速度增加而下降。由于第3.2.1节所述顺时针驻波的存在，相同来流速度下，刚性波面摩擦阻力系数Cτ均比平板小。

边界层内来流经刚性波面，所产生的压差阻力系数Cp随速度增加而增加。但刚性波面总的阻力系数Ct=Cp+Cτ仍然在所有算例中都高于平板，所以刚性波面相对于平板是增阻的。

3.3.2 驻波波面ζ = acoskxcosωt

表3同样显示，随着来流速度提高，驻波波面的摩擦阻力系数与平板一样，是下降的，由于第3.2.2节所述驻涡的存在，Cτ均比平板小。

边界层来流经驻波波面后，同样产生了压差阻力系数Cp。而驻波波面的总阻力系数Ct仍然均高于对应的平板。所以，驻波波面是增阻的。

表3 平板与驻波变形的柔性面阻力对比计算Tab.3 Resistances of rigid plate and active compliant surface with waveform acoskxcosωt

3.3.3 流向随行波波面ζ = acos( kx - ωt)

表4 给出的是随行波面与平板阻力系数的比较。根据第3.2.3 节流动物理过程及机理分析，将重要参数波速c+=与其他参数一起列于表4中。

表4 平板与流向随行波变形的柔性面阻力对比计算Tab.4 Resistances of rigid plate and active compliant surface with waveform acos( kx - ωt)

（1）Case 12与Case 13、Case 19与Case 20是两组除波速外，其他条件完全一样的随行波。计算值比较表明，无论来流是低速还是高速，波速提高，Cτ增加，Cp下降。

（2）Case 12到Case 20算例，结合表3刚性波面情况，可说明：当c+从零开始增加，随行波摩擦阻力系数将从低于平板值增加，约在c+≈0.93 时与平板持平，随后超过平板；而随行波的压差阻力系数将从刚性波Cp＞0开始逐步下降，约在c+≈0.73时开始变为Cp＜0，并继续减小。

（3）随着c+由零增加，随行波总阻力系数Ct=Cp+Cτ从大于平板开始，逐步下降，在C+≈0.63 左右时，达到平板水平；C+继续增加，Ct开始小于平板，并在C+≈1.61,Ct≈0；C+继续增加，Ct＜0。对应的减阻百分数η（正值增阻、负值减阻）：C+＜0.63,η ＞0;C+≈0.63,η ≈0;C+＞0.63,η ＜0。

（4）表2～4数据说明，海豚表皮仅当以流向随行波形式做精细生物运动时才能实现减阻。3.3.4 减阻效率

（1）有用功率

前面的数值模拟是通过给定流向随行波这种柔性壁面的运动形式w( x,t )=̇来求解流场，研究阻力成因。如图11所示，在实际中，总需要力F⇀( x,t )来驱动柔性表皮以实现这种运动w( x,t )。无论是海豚还是仿生体，在减阻时，一定会寻求效率的最大化。若来流速度（或前进速度）为u时，表皮做随行波运动，可减阻Δf，则获得的有用功率为N0= u ⋅Δf。

（2）输入功率

不失一般性，对于流向随行波可以在任意一时刻t0取一个波长λ 内的波面来研究仿生物体输入功率Ni。

为实现流向随行波，此时波面上任意一质点必须具有z向速度w= aω sin( )kx - ωt0。而这样变速运动，波面应该具有数值解给出的P( )x,t0分布。所以海豚或仿生物体必须具有驱动力F( x,t0)dx = P( x,t0)ds ⋅cos θ( x,t0)= P( x,t0)dx 来维持波面存在。即F( x,t0)= P( x,t0)。

图11 随行波柔性面受力分析示意图Fig.11 Diagram of forces on traveling waveform surface

（3）减阻效率η0

定义

式中，Δf ( λ )为一个波长内的减阻值。

表4 给出了在Case 1～Case 9 算例中，c+=0.75 时，减阻效率最大。应该注意的是，表4 结果仅说明：海豚及仿生物体不会或不应该一味追求减阻率；确实存在最佳组合，使流向随行波的减阻效率最高；对于任何一个预期前进速度，特定物体（已有a+，λ+）应该有一个最佳波速c+，使得节能效率最大，对于仿生物体来说将有一个权衡的最佳组合（c+，a+，λ+），使得减阻率与减阻效率均比较理想。

4 结 论

基于前人对海豚表皮微尺度观测结果，本文提出了仿生柔性表皮三种可能的数学模型：刚性波形、驻波波形及流向随行波形。通过数值计算进行了减阻预报和机理分析，获得了以下结论：

（1）RANS方程及动网格技术较好地描述了二维波形壁面的边界层流场，预报了阻力成分；

（2）刚性波、驻波、低波速的流向随行波摩擦阻力系数Cτ小于平板的机理是：对右向来流，在波峰→波谷→波峰形成的凹陷区存在顺时针旋转的驻涡，这降低了壁面右向流速度梯度，甚至部分改变了梯度符号。

（3）流向随行波摩擦阻力系数Cτ随波速增加而增加（由小于平板转而大于平板）的机理是：随行波波面质点始终无流向速度，而波面却以波速在挤压近壁面流体进行流向运动，从而使原本低波速时存在的驻涡逐渐消失，并使壁面速度呈梯度增加。

（4）流向随行波压差阻力系数Cp随波速增加逐渐减小，甚至变向成推力的机理是：波速增加，随行波凹陷区峰→谷波面质点向上运动的速度随之增加，挤压流体加剧而提升波面压力，谷→峰波面质点向下运动速度也随之增加，更快速地让出空间而使该波面压力进一步下降。

（5）刚性波、驻波的总阻力系数Ct都大于平板，流向随行波随波速增加Ct一直不断下降，由大于平板转为小于平板。海豚柔性表皮，唯有流向随行波形式才有可能减阻，仿生航行体MEMS技术应该要有流向随行波功能。

（6）针对不同的来流速度（或者前进速度）具有一定参数特征（a+，λ+）的流向随行波，存在最佳波速，使得减阻效率最大，进化使海豚巡航时会遵循此原则。而对η0寻优，对流向随行波仿生体进行设计具有重要参考价值。

（7）从本质上讲，流向随行波是推力发生器，本文对随行波Cp机理的阐述应该同样适用于蛇形运动等具有随行波鳍的水下生物。

致谢：在此对惠昌年研究员在本文编写过程中提出的宝贵意见表示感谢。