低傅氏数兴波数值预报的不稳定现象及其解决方案
2021-04-24梁川,赵峰
梁 川,赵 峰
(中国船舶科学研究中心,江苏无锡214082)
0 引 言
船舶航行于水面,并伴随有相应的船行波,自由液面的存在是船舶性能数值预报的一个显著特征。很长一段时间内,船舶粘性流动和自由面的计算是分开考虑的,即用势流理论方法处理自由面兴波,而另外通过求解RANS 方程来计算船体的粘性边界层,这种分离处理的方法,不能考虑粘性和自由面之间的耦合作用。随着计算机性能的快速提升和相关CFD 算法的深入发展,特别是诸如VOF、Level Set 等自由面捕捉方法的发展和成熟,使得同时考虑粘性和自由液面影响的船舶CFD 技术获得了长足的进步,取得了众多应用成果[1-7],并愈来愈朝着数值水池应用愿景方向发展[8-9]。
傅氏(Froude)数(式(1))是一个衡量流体惯性力与约化重力(流体质点受到重力与浮力的合力,在其他位置为零,在自由面存在一个阶跃)比值的无量纲参数,是一个区分船舶性能与类别的重要参数,其区分定性作用类似于航空中的马赫(Mach)数。

在采用CFD 技术进行船舶水动力性能研究时,其难点主要在Froude 数范围的两端,即高傅氏数(Fr>0.5)和低傅氏数(Fr<0.15)工况。
高傅氏数船舶常见于一些高速快艇,其计算难点主要在于船体兴波作用很大、船体姿态变化剧烈、船体运动与兴波作用强烈耦合等非线性特征突出,相关的CFD技术在不断研究和发展中。低傅氏数船舶常见于大型油轮和超大散货船,随着船舶绿色环保理念的提升,运输船舶越来越向大型化方向发展,对于低傅氏数船舶性能的数值预报也越来越具有显著的工程价值。低傅氏数工况的计算难点主要在于随着Froude 数越来越低,计算将变得越来越不稳定,且这一不稳定现象,在自研求解器或者商用求解器(如CFX,Fluent和StarCCM+等)中普遍存在。
在低傅氏数船舶粘流数值模拟方面,已有不少学者进行了相关研究。典型的如Toxopeus 等[5],统计研究了四款主流求解器(MARIN 水池的ReFRESCO、Iowa大学的CFDSHIP、ECN 大学的ISIS-CFD 和商用软件STAR-CCM+)对标模KVLCC2 做偏航运动模拟(聚焦于Fr=0.064 2 工况)的流动情况,其中,ReFRESCO 和CFDSHIP 未考虑自由面影响,ISIS-CFD 和STAR-CCM+对自由面进行了考虑,不过文中未提及考虑自由面后可能出现的计算不稳定现象。
目前,关于该不稳定现象的文献报导很少,分析和解释这一现象的更少。这主要是当Froude数较低时,自由面兴波的作用较小,通常会当做叠模(自由面处设置为对称边界条件)来进行处理。然而,针对该问题的深化研究除了理论上解释关于某个计算现象的疑问外,同时也有其实际应用价值:(1)低傅氏数工况,兴波阻力虽较小但并不表示不存在,而且自由面的存在对粘压阻力存在一定影响,比如水池试验获取船舶形状因子的方法主要在低傅氏数段进行,目前ITTC 推荐方法经常失效的一些特殊情况(球艏贴近水面,方尾浸没),均与自由面对粘压阻力的影响有关;(2)对于船舶在波浪中低速航行的工况,自由面将无法采用叠模处理。
本文将针对低傅氏数工况兴波数值预报不稳定的现象展开相关研究,尝试分析其背后的数值机理,并提出相应的解决方案。
1 现象描述
笔者在进行DTMB5415标模(CFD WorkShop 2010标模[4],高、中、低三个典型航速算例分别对应Fr=0.41、0.28 和0.138)阻力计算时,发现低Froude 数工况计算反常,留心记录并与相关业内人士交流讨论后,发现这个现象在船舶CFD 模拟中普遍存在,是一类共性问题。其主要表现为:(1)计算波形十分反常,且随计算时间增加兴波范围和幅度越来越大;(2)计算的阻力曲线波动很大,总体来看是计算不稳定的典型特征。
由于本文所关注的低傅氏数工况兴波数值预报不稳定现象在诸多CFD求解器中普遍存在,因此,关于本文所采用的CFD 方法只作一个简要介绍:基于求解不可压RANS方程的CFD 求解器、计算网格生成采用重叠网格技术、自由面处理采用Level Set方法。在数值实践初期,采用平时初步总结出的一套参数设置进行计算,也称为常规设置,如表1所示。下面以标模DTMB5415在Fr=0.138和Fr=0.28时举例说明相关现象。

表1 阻力计算常规参数设置Tab.1 Regular CFD settings for resistance computation
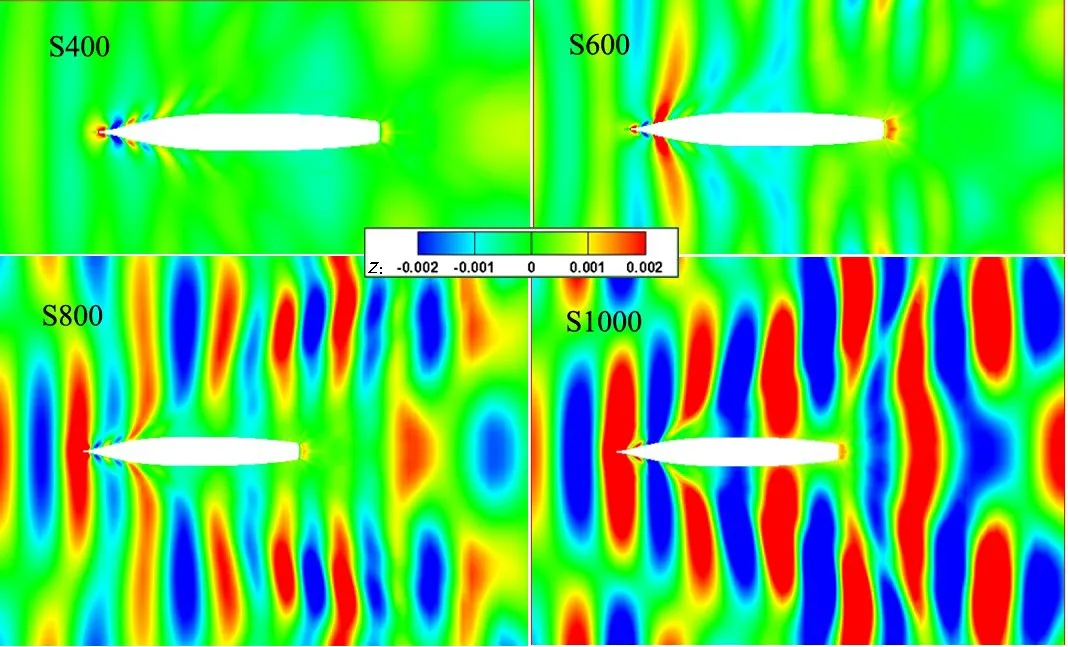
图1 Fr=0.138工况常规设置下不同时间步的波形对比Fig.1 Comparison of wave contours at different time steps with the regular settings when Fr=0.138

图2 Fr=0.28工况常规设置下不同时间步的波形对比Fig.2 Comparison of wave contours at different time steps with the regular settings when Fr=0.28
图1 为Fr=0.138 工况,常规设置下不同时间步的波形对比图,随着时间的推移,波动的范围和幅度越来越大,波面的能量越来越积聚,这与真实的低傅氏数兴波很小的特征明显不符;图2 为Fr=0.28 工况的波形对比图,可以看出,波形变化稳定,与物理直观相符。
图3为Fr=0.138和Fr=0.28工况总阻力系数随时间变化曲线。可以看到,Fr=0.28时波动的幅值更小且呈逐渐缩小趋势,而Fr=0.138时波动振幅很大(通常Froude数越低,振幅越小),且波峰波谷的包络线呈震荡变化。
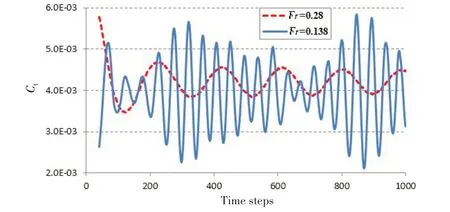
图3 常规设置Fr=0.138和Fr=0.28工况总阻力系数随时间变化对比Fig.3 Comparison of Ct curve over time steps with the regular settings when Fr=0.138 and Fr=0.28
上述种种现象表明,在同样采用常规设置情况下,低傅氏数(Fr=0.138)工况的计算出现了非常明显的不稳定现象。
2 控制方程离散格式数值分析
出现上述现象是因为在比较低的傅氏数下计算,其计算稳定性不如高傅氏数情况,而计算稳定性与控制方程的离散格式的数值特性密切相关,特别是差分格式的数值耗散特性,具体可以参见相关教材[10-12]。
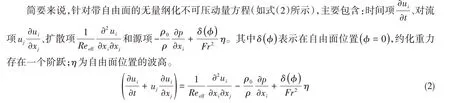
需要通过离散差分来近似表达各微分项,离散格式和原微分形式之间的差异(更高阶的数值耗散或者数值色散项)将影响数值计算的特性。特别是偶数阶的数值耗散项,将很大程度上影响计算的稳定性。
一般来说,采用隐式格式或者迎风格式将产生数值耗散(数值粘性),增加计算稳定性;采用显式格式则会产生数值逆耗散,增加计算不稳定性,如控制方程中不同变量的分离求解(即通过采用上一时间步的结果,假设其他变量已知,然后轮流求解当前变量,并通过不断迭代达到收敛),将引入不稳定因素。在不可压N-S 方程求解中,一般采用分离求解的策略,如式(2)中的源项,即采用显式处理,从而引入不稳定因素。
针对控制方程(式(2)),按照常规设置的离散格式(时间二阶隐式格式、对流二阶迎风格式、扩散项二阶中心差分格式、源项采用显式处理)进行数值耗散项(离散格式和原微分形式之间差异中的偶数阶微分项)分析。
以时间项为例,二阶隐式差分格式与原微分项的差值为

暂不关注其他项,不难推导出式(2)的数值耗散形式,如式(6)所示:
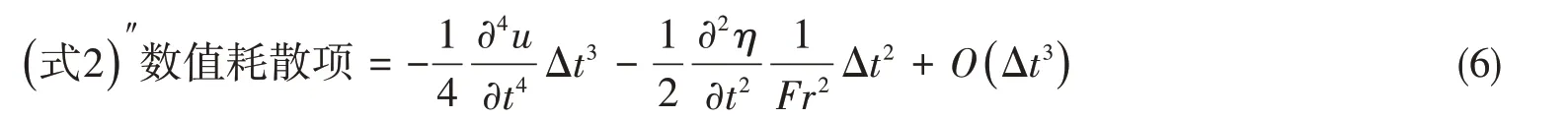
另外,同理易得时间项采用一阶隐式的数值耗散形式,如式(7)所示:
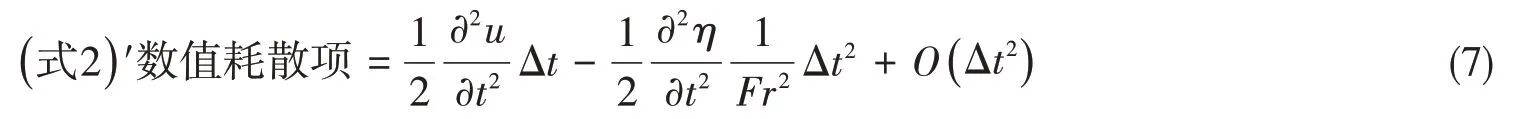
3 源于理论指导的数值实践
与Froude 数相关的逆耗散项有使计算发散的趋势,因此数值实践的思路可围绕如何来抑制这一趋势展开,包括两个方面,一是增加数值正耗散,另一个是减小数值逆耗散。
增加正耗散:一个是增加时间项耗散,比如时间差分由二阶隐式改为一阶隐式,实际上对于阻力计算这种稳态问题,用一阶格式比较合适;另一个是增加对流项耗散,比如由二阶格式改为一阶格式,但是这种方法对计算结果影响较大,要慎用。
减小逆耗散:从逆耗散项的表达式中可以看到,减小时间步长Δt可以减小逆耗散。
图4 为在常规设置基础上,分别将时间项改为一阶隐式(图4(c))、将时间步长缩小5 倍取Δt=0.002(图4(b))与常规设置(图4(a))在相同来流时间下的波形对比图,另将三者在y=0.08Lpp处的波形曲线绘制于图4(d)。可以看到,和常规设置相比,大范围的不合理波动均得到了不同程度的抑制,其中,采用时间一阶隐式的方案在船体周围展现的合理波形更加丰富,缩小5倍时间步长的方案在船体外围仍存在一些不合理的波动。仔细分析数值耗散公式(式(6))会发现:减小时间步长既会减小逆耗散,同时也会减小时间项正耗散;单纯增加正耗散(时间二阶隐式改一阶隐式)效果最好。
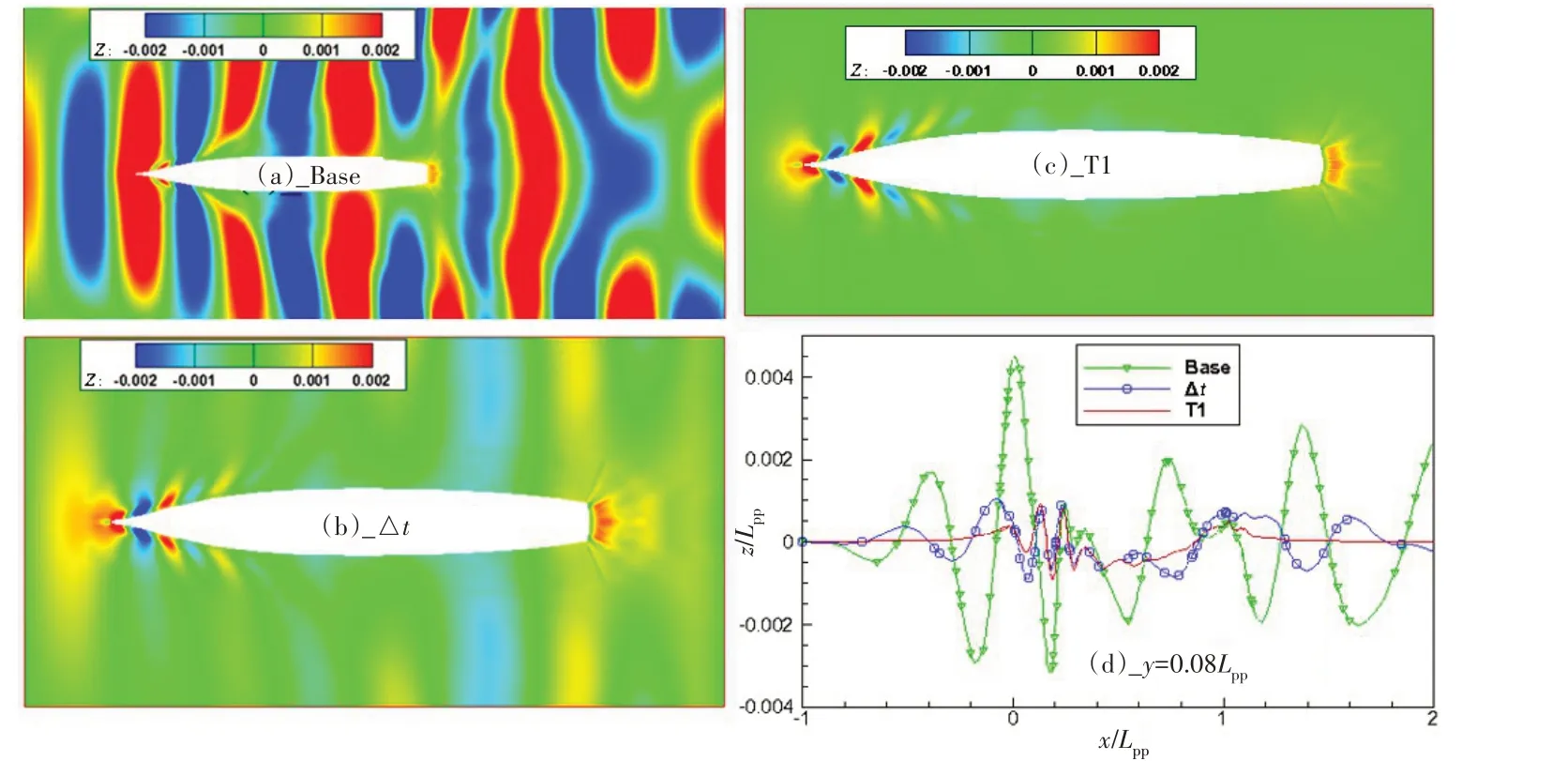
图4 Fr=0.138工况不同参数设置的波形对比图Fig.4 Comparison of wave contours with the different settings when Fr=0.138
图5 是Fr=0.138 工况不同设置下总阻力系数随时间变化曲线,可以看到:与常规方案相比,采用时间一阶隐式的方案,波动的幅度大幅缩小,并最终趋于稳定;从总阻力系数的平均值来看,两者相差无几,且与试验值吻合良好。
另外,从正常的低傅氏数流动的波形范围和波高幅值来看,傅氏数越低,波形范围越小(波长越短,且主要集中在船首附近)、波高幅值也越小。因此,在进行网格划分时,为了能够捕捉到自由面处的流动,自由面位置常需要布置更加细密的网格,具体为水平方向重点对船体首尾区域加密,同时垂直方向也需进行适当加密。由于本文常规设置的自由面网格已经采用了较好的加密布置,本文未进行自由面网格加密的数值对比实践。
图6 是Fr=0.28 工况,时间一阶隐式和常规设置下总阻力系数随时间变化曲线,可以看到曲线的波动幅度相差不大,一阶隐式略小,这与Fr=0.138 工况差异明显,从侧面验证了计算稳定性与Froude数平方呈反比的理论推导,也指出低傅氏数的不稳定现象尤其值得关注。
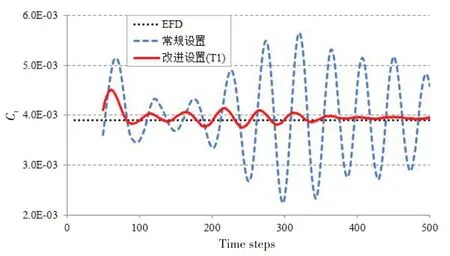
图5 Fr=0.138工况不同设置下总阻力系数随时间变化曲线Fig.5 Comparison of Ct curves over time steps with the different settings when Fr=0.138

图6 Fr=0.28工况不同设置下总阻力系数随时间变化曲线Fig.6 Comparison of Ct curves over time steps with the different settings when Fr=0.28
另外,由自由面产生的逆耗散项形式可知,当Froude 数持续降低,逆耗散项将持续平方指数增大。此时,单独靠一种方式将很难控制计算稳定性,需要多种方式联合使用,例如在使用时间一阶隐式的同时,还需要减小时间步长。
图7 为在Fr=0.1 时,时间均采用一阶隐式、时间步长分别为Δt=0.01 和Δt=0.005 时,总阻力系数随时间变化曲线。可以看到:在Δt=0.01时,即使采用时间一阶隐式格式,总阻力曲线也会出现比较大幅度的高频振荡;当Δt=0.005 时,曲线才变得光滑。当Froude 数继续降低,经测试,Fr=0.05 时,在采用一阶隐式时间格式的同时,时间步长需取Δt=0.002才能获得光滑的结果。

图7 Fr=0.1工况不同设置下总阻力系数随时间变化曲线Fig.7 Comparison of Ct curves over time steps with the different settings when Fr=0.1
4 结 论
本文针对船舶在低傅氏数兴波数值预报中容易出现计算不稳定的普遍现象展开了相关研究,从控制方程离散差分格式出发,推导出船舶CFD所特有的(带自由面)不稳定项形式,从理论上来解释这一现象。同时,根据所推导的数值耗散项的表达形式,进行了充分的数值实践研究,提出了低Froude数计算稳定性的控制策略供相关从业人员参考借鉴:
(1)对于阻力计算这类稳态问题,适合于采用时间一阶隐式格式;
(2)减小时间步长能够有效抑制发散;
(3)适当加密自由面附近的网格;
(4)综合应用上面三种策略。
需要说明的是,由于控制策略的具体细化与所采用的求解器有很强的关联性,当遇到低傅氏数计算不稳定问题时,本文所给的策略将起到一个方向指引的作用。
致谢:本文的完成也得益于与吴乘胜研究员、李胜忠研究员、邱耿耀高级工程师、蒋一工程师以及其他相关科研人员的启发性交流,作者在此对他们的贡献表示由衷的感谢!
