水下仿生柔性胸鳍摆动水动力特性试验研究

张纪华，刘乐华，杨晓光，马雪泉

（1.北京机电工程研究所，北京100074；2.上海船舶运输科学研究所，上海200135）

0 引 言

水下仿生潜航器具有高效推进、高机动等良好性能，仿生胸鳍推进是模仿鱼类左右对称的柔性胸鳍运动而兴起的一种仿生推进模式，典型的海洋生物是俗称“魔鬼鱼”的蝠鲼。针对水下仿生胸鳍推进集成，日本科研工作者Imae采用柔性乙烯树脂薄膜和淬火钢带，以刚性双四杆机构驱动胸鳍前缘带动胸鳍鳍面实现摆动运动[1]；德国Festo 公司研制了胸鳍摆动的仿生鱼Aqua_ray[2]；新加坡国立大学选用PVC 片材料作为胸鳍研制了MantaDroid 仿蝠鲼机器鱼[3]，并完成了长航时的续航试验；新加坡南洋理工大学与中国国防科学技术大学联合开发了仿蝠鲼机器鱼，样机两侧胸鳍分别由三组独立控制的具有一定柔性的鳍条驱动，并采用类鱼漂的机构进行深度控制[4]；国防科技大学采用多鳍条驱动方式研制了仿胸鳍样机[5]；哈尔滨工业大学研制了SMA 驱动的仿蝠鲼机器鱼[6-7]，实现了高稳定性和无噪声推进；北京航空航天大学研制了多型仿牛鼻鲼Robo_Ray样机[8]，并自行搭建了小型测力实验水槽[9]，完成了样机水池游动试验和样机测力试验。现有的研究成果中，仿生胸鳍推进样机侧重于仿生机构设计、无模型的仿生胸鳍推进游动控制及系统集成[10]等，从研制流程上基本忽略了仿生胸鳍推进水动力设计这一极为关键的环节，这也是造成仿生胸鳍推进效率低下的重要原因。此外，对于仿生胸鳍推进水动力特性的研究，还主要依赖于流场的数值计算，且数值仿真计算缺乏柔性材质的胸鳍与水流相互作用，造成水动力数据失真。为此，本文通过研制仿生柔性胸鳍模型及驱动控制系统，搭建试验测试系统，采用拖曳水池测力试验的方法对仿生柔性胸鳍摆动过程受力进行测试，获得仿生柔性胸鳍在不同运动参数时的受力数据。

1 试验装置与方法

1.1 试验水池

试验水池选择上海船舶运输科学研究所船模拖曳试验水池，如图1所示。水池主要参数为：总长192 m，有效试验长度160 m，宽10 m，水深4 m，拖车运行速度0.01～10 m/s。试验水池配备NI 公司集成化数据实时采集分析系统。

1.2 试验模型

1.2.1 物理模型

本文依据生物胸鳍原型轮廓，研制了仿生柔性胸鳍试验模型，如图2 所示。该模型由鳍条、硅橡胶蒙皮经过浇筑、固化和脱膜等过程制作而成，硅橡胶确保试验模型产生柔性光滑的变形运动。

试验模型展长为1.29 m，根部最大弦长为1.1 m，根部剖面最大厚度为0.24 m。仿生胸鳍试验模型的前、中、后三根鳍条外接三个伺服电动缸，试验模型在电动缸推拉丝杠同步往复运动的带动下产生左右摆动，在电动缸推拉丝杠异步等时差往复运动的带动下产生左右摆动和鳍面扭转，调节电动缸丝杠线位移、频率以及异步时间差实现试验模型运动参数和运动形态的变化。

1.2.2 模型运动

仿生胸鳍试验模型运动由三根鳍条带动，本文设计了鳍条的正弦周期性运动规律如下：

图1 船模拖曳试验水池Fig.1 Ship model towing tank

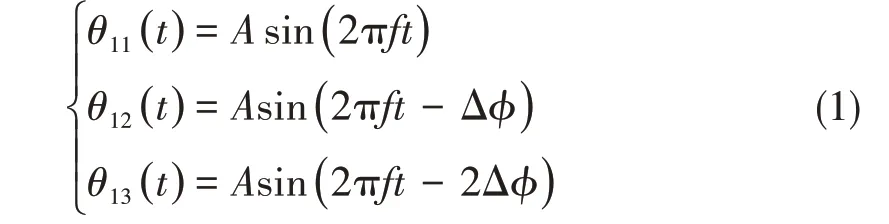
图2 仿生胸鳍试验模型Fig.2 Experimental model of bionic flexible pectoral

式中，θ11，θ12，θ13分别为前中后三根鳍条与铅垂面的夹角；A 为角度幅值，单位为°；f为摆动频率，单位为Hz；Δϕ为相邻鳍条间的相位差，单位为°。图3为前中后鳍条运动定义，Fx和Fy分别为模型受到的推力和侧向力。

1.3 试验模型安装

试验模型安装如图4 所示。仿生柔性胸鳍试验模型的前、中、后鳍条与对应的电动缸相连，形成仿生胸鳍运动系统。整个运动系统以竖直垂吊的方式通过测力天平传感器、支撑板等连接，被固定在水池拖车的模型安装测试机构上。鳍面转动轴心与水面齐平，试验时随着拖车沿导轨在水池内前后运动。此时模型全部浸没在水池中，且其摆动过程中不会露出水面产生额外的兴波阻力干扰。支撑和驱动作用的电动缸直线推杆会在水面以上滑行，但其产生的兴波阻力相比于模型全沾湿受到的力而言比重较小，暂时可忽略其影响。

仿生胸鳍试验模型拖曳水池测力试验包含两部分运动，一部分是外部运动，一部分是自身运动。外部运动的产生源于水池拖车的带动，沿导轨方向在水池内前后运动。试验模型自身的运动依靠前、中、后鳍条的运动牵连产生，具体实现是：各鳍条在电动缸的带动下，以鳍条根部为支撑点，左右摆动，实现沿展长方向的摆动；前、中、后鳍条在电动缸异步相位（通过设置启动时间延迟实现）驱动的带动下，实现鳍面的扭转。通过改变电动缸的频率、施加到鳍条上的驱动位移、异步相位差等参数，可实现仿生胸鳍试验模型运动频率、摆动幅值和相位差的变化。测力天平传感器感受仿生胸鳍试验模型受到的电压变化信号，并通过电线、信号采集器输送到计算机，完成试验数据的采集与处理。

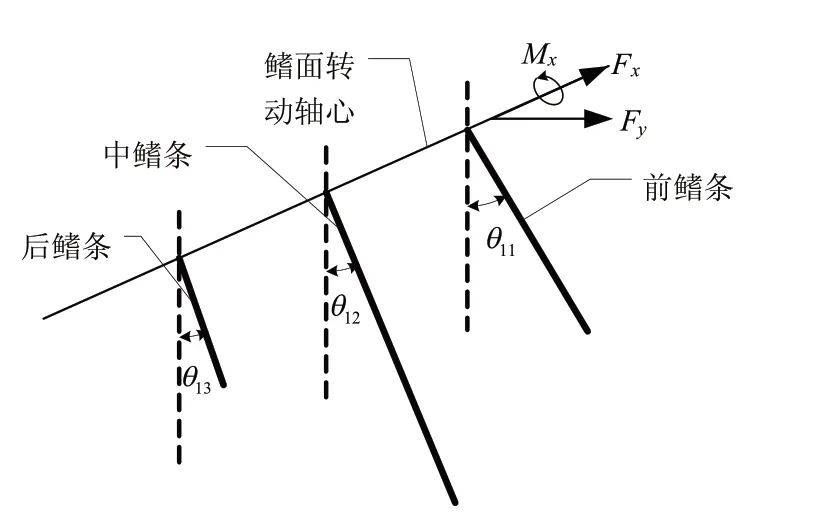
图3 前中后鳍条运动定义Fig.3 Locomotion definition of front fin,middle fin and back fins

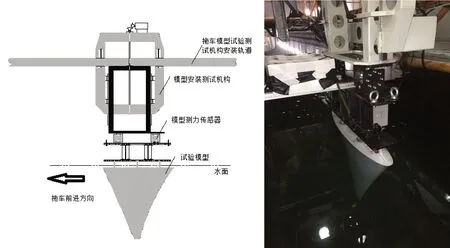
图4 试验模型安装Fig.4 Installation of experimental model

1.4 测力天平传感器

试验天平传感器（如图5 所示）采集频率为200 Hz，三通道最大量程分别为：推力Fx测量通道1.5 kN、侧向力Fy测量通道1.5 kN、扭矩Mx测量通道0.16 kN⋅m，单向测力精度为0.5%，串扰度误差小于2%。

为了提高测力试验平台与仿生胸鳍试验模型连接的刚度，采用两个三分力天平传感器串联。两个天平传感器前后共轴线布置，并与仿生胸鳍试验模型转动轴线平行且共平面，以便于数据处理时力与力矩的解算。测力天平传感器可以测量模型受到的水平轴向力和垂直于试验模型鳍面的侧向以及绕试验模型转轴转动的扭矩。试验模型受力与天平测量数据的关系为

式中，Fx1、Fy1、Mx1、Fx2、Fy2、Mx2分别为测力天平1、测力天平2 采集的力和力矩信号；h 表示测力天平传感器轴心到模型转动轴的距离。

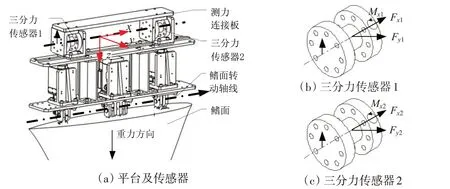
图5 测力天平传感器Fig.5 Force balance

1.5 试验方法

仿生柔性胸鳍摆动拖曳水池试验过程中，首先将拖车开至船坞，完成试验模型与拖车的固定连接（胸鳍尖端距离水池底部2 m 左右），检查无误后将拖车缓慢开至预定港位；然后电动缸上电，胸鳍运动控制发控系统（如图6 所示）按照预定工况发出电动缸作动指令，电动缸单向启动至丝杠的最大位置，延迟30 s后鳍条在电动缸的带动下在铅垂面内产生周期性左右摆动，拖车延时60 s后启动并缓慢加速至试验速度；最后待拖车速度稳定后，测力天平传感器采集胸鳍受力的电压信号，通过信号转换获得模型受的力和力矩，截取几个周期内的数据作为最终结果。通过控制电动缸输出的频率、输出轴位移以及3个电动缸之间作动时间间隔获得鳍条不同频率、摆幅和相位差。

试验过程中，拖车速度保持为0.4 m/s，对应流动的雷诺数Re为5.16×105。

图6 上位机控制界面Fig.6 PC control interface

2 试验结果分析

2.1 仿生胸鳍运动形态分析

图7给出了仿生胸鳍典型摆动工况下仿生柔性胸鳍模型的形状变化图像。仿生胸鳍在驱动系统的带动下产生了左右摆动+鳍面扭转耦合的主动柔性大变形，模型胸鳍尖端的薄壁区域受到水流的阻滞作用，发生了较为严重的不规则被动变形，此现象较好地反映了胸鳍的柔性特征。

图7 水下仿生胸鳍摆动形态图像Fig.7 Shape image of underwater bionic pectoral fin oscillation

2.2 流场形态分析

图8 给出了仿生胸鳍典型摆动工况下尾流场形态。在尾流场中产生了明显的尾涡，相邻尾涡的旋向相反，并沿仿生胸鳍转轴中心线等间距排布，对比图8（b）中卡门涡街形态，仿生胸鳍摆动尾涡呈现与卡门涡街旋转方向相反的结构特征，可称之为反卡门涡街形态，这也是仿生摆动推力产生的根源。分析系列的试验图像发现（见图9～10），摆动频率越大，尾流中相邻涡核水平间距L 越小；摆动角度幅值越大，尾流中相邻涡核纵向间距H越大。

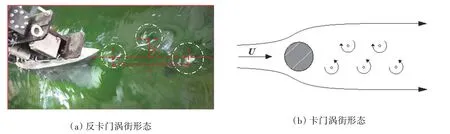
图8 尾涡流场试验图像Fig.8 Experimental image of vortex flow

图9 不同频率下涡核水平位置Fig.9 The horizontal distribution of vortex core region under different frequencies

图10 不同摆动角度下涡核纵向位置Fig.10 The vertical distribution of vortex core region under different swing angle

2.3 水动力特性分析

2.3.1 水动力参数定义

此外，定义Ct_max、Ct_min 分别为推力系数周期性震荡幅值的最大和最小值，Cn_max、Cm_max 分别为侧向力系数、力矩系数周期性震荡幅值的最大值（最小值与最大值的绝对值相等）。

2.3.2 运动频率影响

图11给出了仿生胸鳍模型不同摆动频率下（分别为0.2、0.3、0.4 Hz，此时拖车速度、摆动角度和相位差均一致）的水动力特性变化曲线，图中曲线的负值代表正推力（与运动方向相反，下同）。图中结果表明：频率越大，推力曲线Ct峰值和均值也越大（由负推力变为正推力）、侧向力曲线Cn和绕胸鳍转动轴的力矩曲线Cm峰值也越大；仿生胸鳍摆动过程中柔性鳍面受到流体力的作用，胸鳍材料产生明显的弹性变形（0.4 Hz工况下尤为明显），导致整个胸鳍发生不规则形状变化影响，推力曲线Ct在均值上下呈现不对称现象，均值线以上Ct曲线时间行程较长，且频率越大，这种非对称现象越显著；侧向力曲线Cn和力矩曲线Cm受鳍面不规则形状变化影响较小，呈现较好的正弦变化特征。

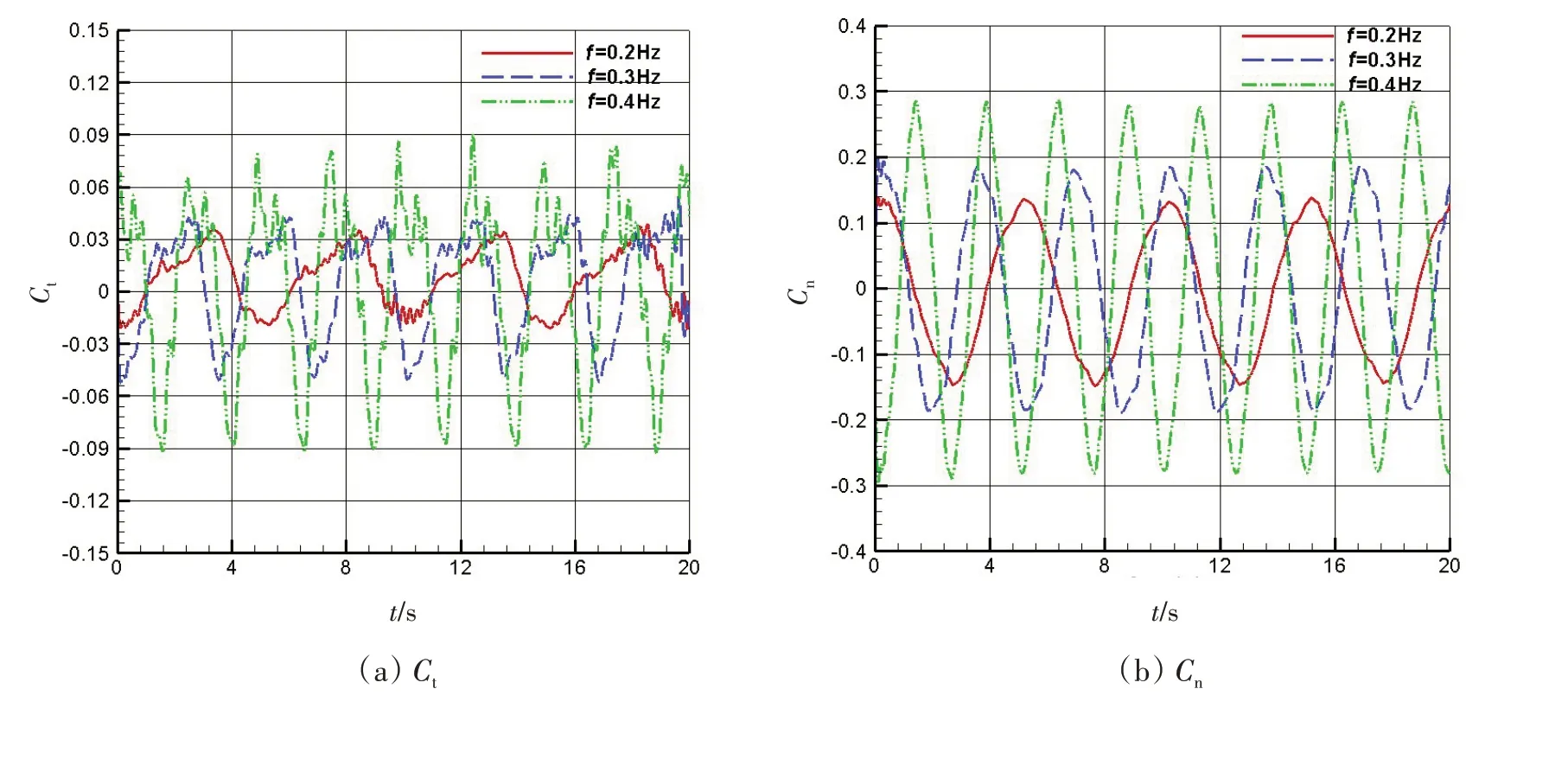
图11 频率对水动力参数影响曲线Fig.11 The hydrodynamic parameter curves under different frequencies

将各力系数在周期内进行平均计算，获得力系数周期均值随柔性胸鳍运动频率变化关系，如图12所示。图中，无量纲推力均值为正，代表此时试验模型受到的水动力为阻力（下同）。随着频率的增大，柔性胸鳍受到的正向推力均值在减小，表示此时净推力在增大，即推力均值随频率增大而近似线性增大。此外，各力和力矩系数周期振荡的最大幅值随频率增大而近似线性增大。

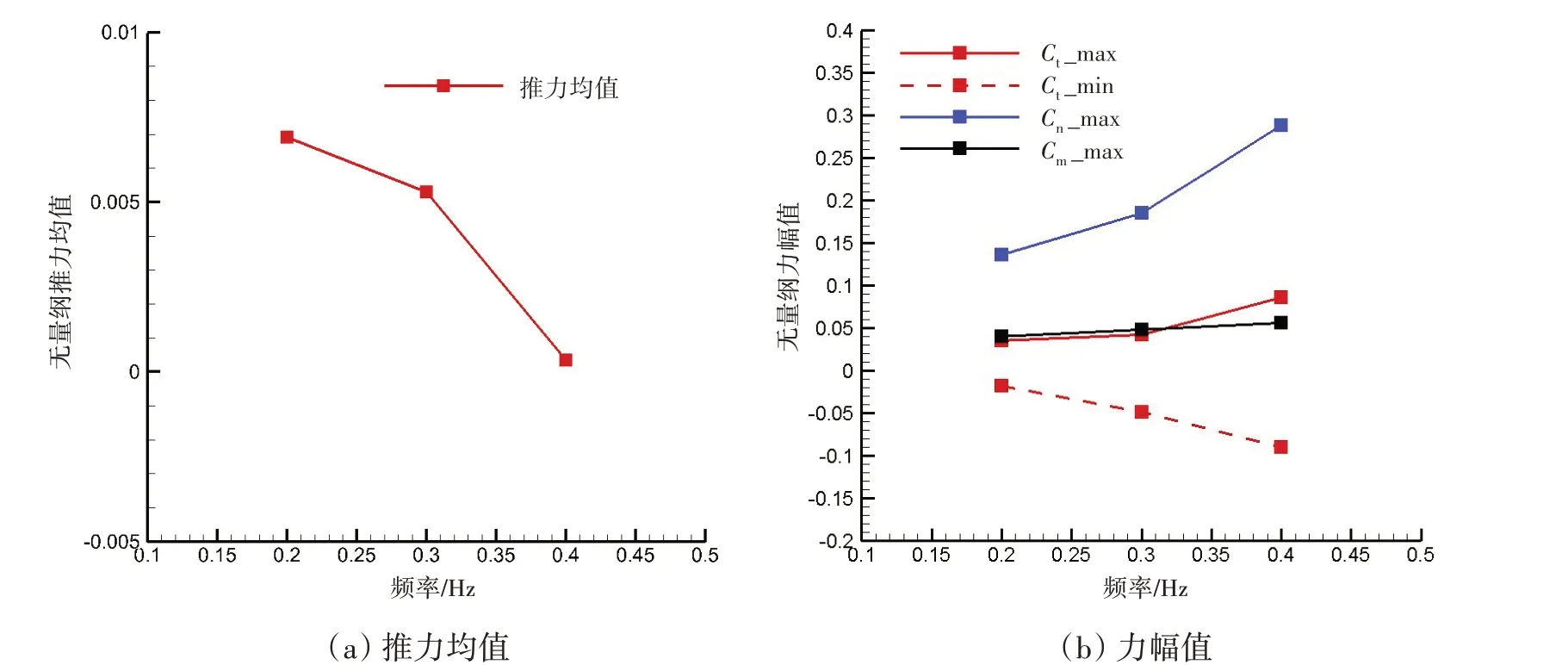
图12 频率对水动力参数均值、幅值影响曲线Fig.12 Influence of frequency on the average and the amplitude of hydrodynamic parameters

2.3.3 摆动角度幅值影响

图13给出了仿生胸鳍模型不同摆动角度下（此时拖车速度、摆动频率和相位差均一致）水动力特性变化曲线。图中曲线表明：摆动角度越大，推力曲线Ct峰值和均值也越大（由负推力变为正推力）、侧向力曲线Cn和绕胸鳍转动轴的力矩曲线Cm峰值也越大；与水动力曲线受频率影响变化特性类似，柔性鳍面不规则形状变化引起了推力曲线Ct均值上下曲线呈现不对称现象，摆动角度越大，非对称现象越显著；侧向力曲线Cn和力矩曲线Cm受鳍面不规则形状变化影响较小，呈现较好的正弦变化特征。

图14给出了力系数周期均值随柔性胸鳍摆动角度变化关系。随着摆动角度的增大，柔性胸鳍受到的正向推力均值也在减小，表示此时净推力在增大，即推力均值随摆动角度增大而近似线性增大。此外，各力和力矩系数周期振荡的最大幅值随摆动角度的增大而近似线性增大。

图13 摆动角度对水动力参数影响曲线Fig.13 Influence of swing angle on hydrodynamic parameters

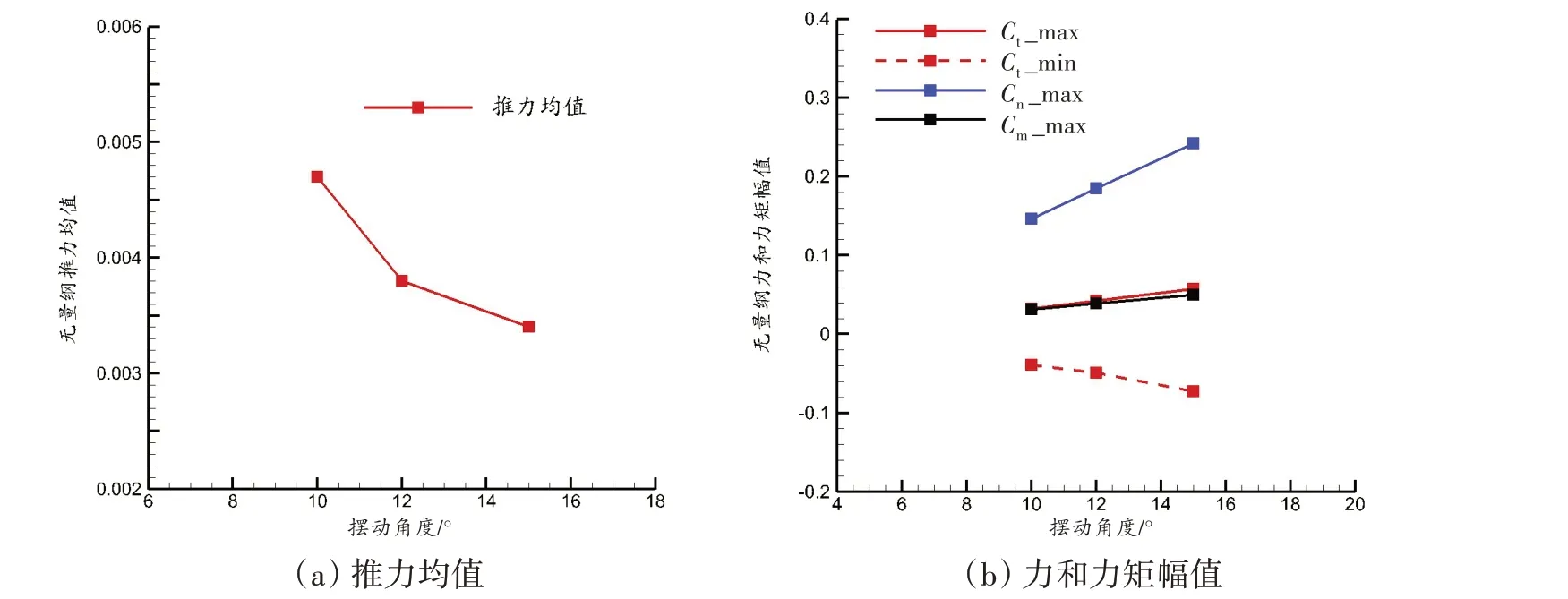
图14 摆动角度对水动力参数均值、幅值影响曲线Fig.14 Influence of swing angle on the average and the amplitude of hydrodynamic parameters

2.3.4 相位差影响

图15给出了仿生胸鳍模型不同相位差下（此时拖车速度、摆动频率和摆动角度一致）水动力特性变化曲线。图中曲线表明：相位差越小（此时对应鳍面整体扭转较小），推力曲线Ct峰值越大、侧向力曲线Cn和绕胸鳍转动轴的力矩曲线Cm峰值也越大；与水动力曲线受频率影响变化特性类似，柔性鳍面不规则形状变化引起了推力曲线Ct在均值上下呈现不对称现象，均值线以上Ct曲线时间行程较长，相位差越小，非对称现象越显著；侧向力曲线Cn和力矩曲线Cm受鳍面不规则形状变化影响较小，呈现较好的正弦变化特征。

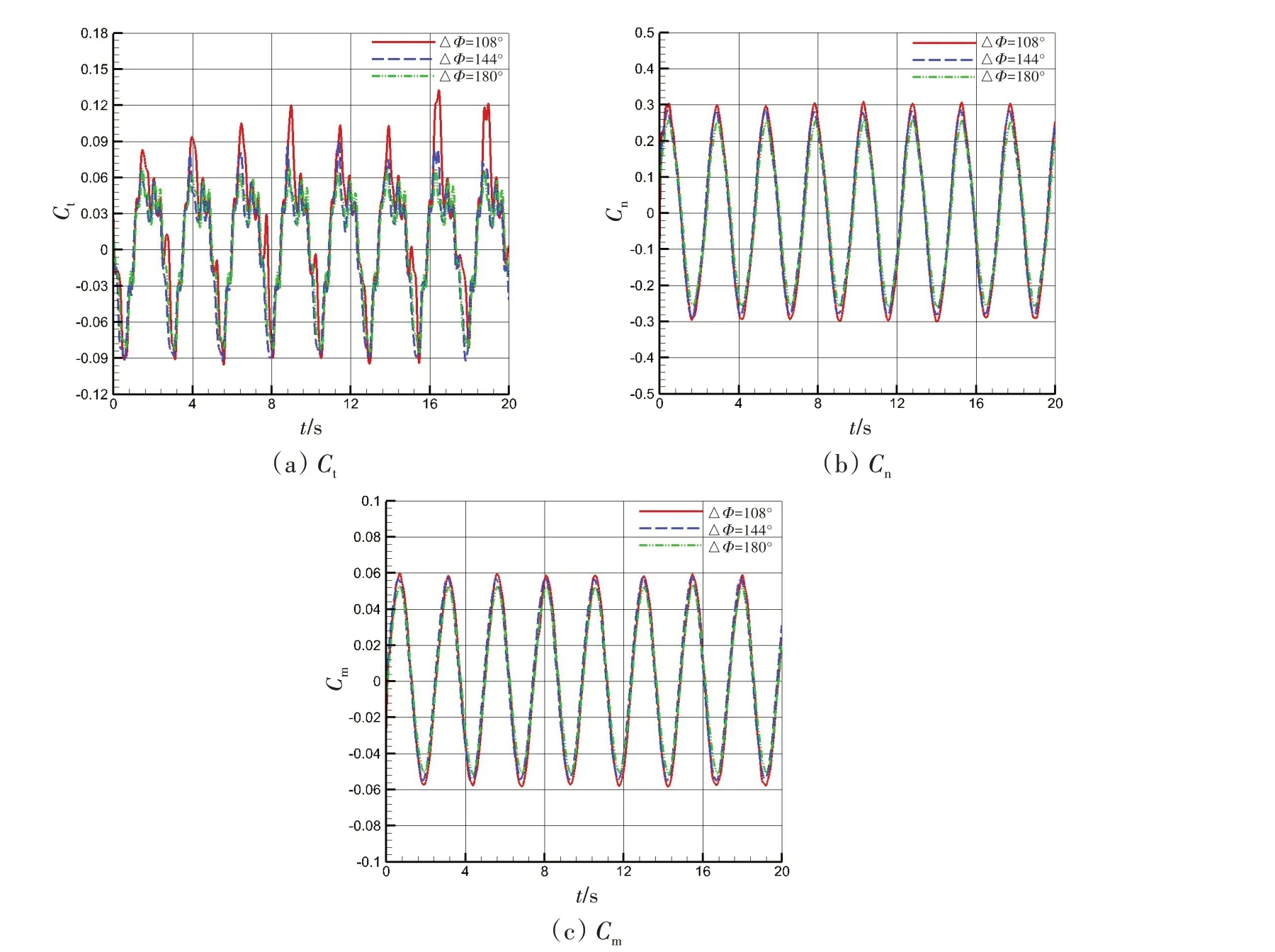
图15 相位差对水动力参数影响曲线Fig.15 Influence of phase difference on hydrodynamic parameters

图16给出了力系数周期均值随柔性胸鳍运动相位差变化关系。随着相位差角度的增大，柔性胸鳍受到的正向推力均值呈现先减小后增大现象，表示此时净推力先增大后减小，即存在一个最佳相位差，使柔性胸鳍推力达到最大值。各力和力矩系数周期振荡的最大幅值随相位差变化减小。

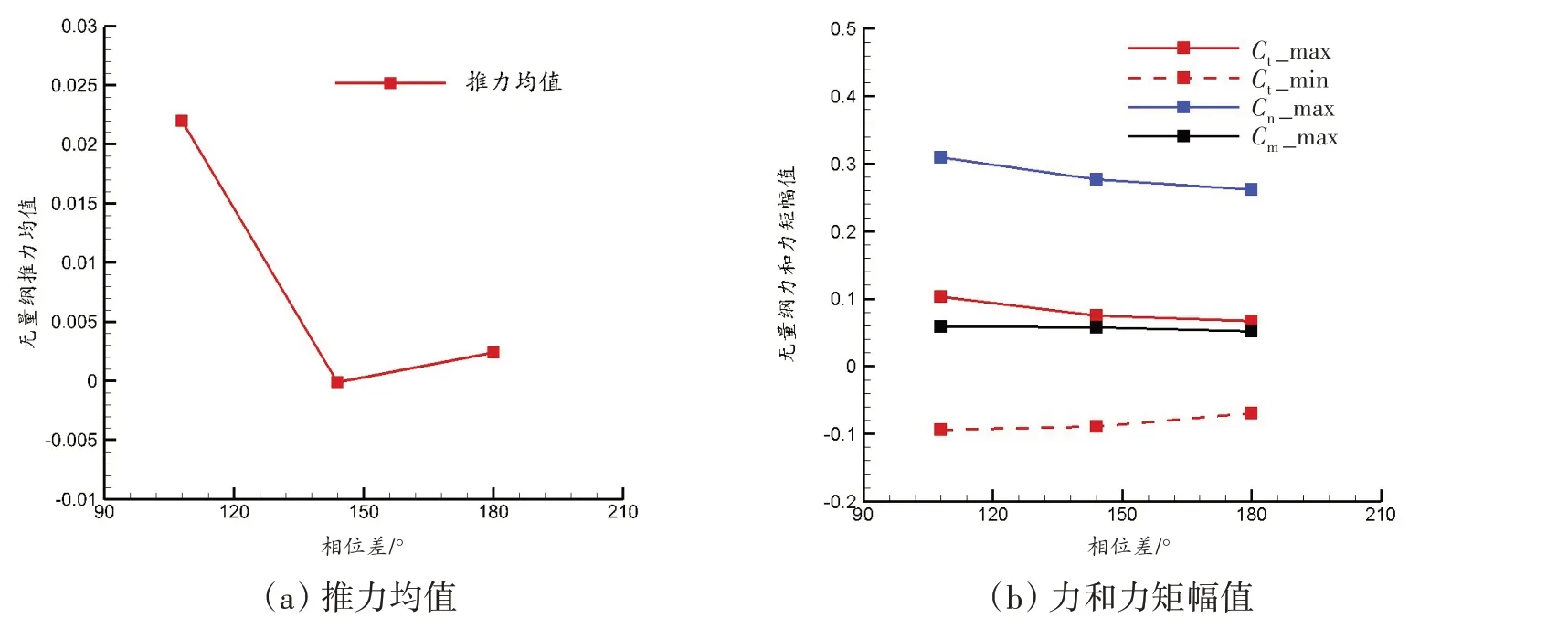
图16 相位差对水动力参数均值、幅值影响曲线Fig.16 Influence of phase difference on the average and the amplitude of hydrodynamic parameters

3 结 论

本文针对仿生柔性胸鳍推进模式下水动力特性研究，研制了仿生柔性胸鳍测力试验模型及驱动控制系统，首次在大型拖曳水池环境下完成了仿生胸鳍摆动过程测力试验，试验测试了频率、摆动角度、相位差等因素对仿生胸鳍模型水动力的影响，通过试验结果的分析获得如下结论：

（1）仿生柔性胸鳍模型摆动过程中受到水流的阻滞作用，模型胸鳍尖端的薄壁区域发生了较为严重的不规则被动变形，此现象较好地反映了胸鳍的柔性特征。

（2）仿生胸鳍摆动过程中，在尾流场中产生明显的反卡门涡街，且摆动频率越大，相邻涡核水平间距就越小；摆动角度幅值越大，相邻涡核纵向间距就越大。

（3）仿生胸鳍摆动频率越大、摆动角度越大、胸鳍鳍条间的相位差越小，胸鳍产生的推力、侧向力和转动力矩峰值就越大；受仿生胸鳍摆动过程柔性鳍面不规则形状变化的影响，推力曲线Ct在均值上下呈现不对称现象，频率越大、摆动角度越大、相位差越小，非对称现象就越显著；侧向力曲线Cn、力矩曲线Cm受鳍面不规则形状变化影响较小，呈现较好的正弦变化特征。

（4）频率越大、摆动角度越大，柔性胸鳍净推力就越增大，且推力均值、各力和力矩系数周期振荡的最大幅值随频率、摆动角度增大而近似线性增大。

（5）相位差越大，柔性胸鳍净推力先增大后减小，各力和力矩系数周期振荡的最大幅值也减小。可以推断，存在一个最佳相位差，使柔性胸鳍推力达到最大值。