仿生胸鳍的三维尾涡结构与参数影响分析

2020-04-10李宁宇苏广胜赵云鹤孙向东张嗣祺苏玉民

海洋工程 2020年1期

李宁宇，苏广胜，赵云鹤，孙向东，张嗣祺，苏玉民

(1. 哈尔滨工程大学水下机器人技术重点实验室，黑龙江哈尔滨 150001; 2. 中国石油天然气管道工程有限公司，河北廊坊 065000; 3. 杭州和利时自动化有限公司，浙江杭州 310000)

近年来，利用鱼类游动的推进机理所研制的仿生水下机器人在海底地形扫描、海洋资源开发等领域的应用日益增多。就游动时所依靠的生理部位来讲，可分为身体和/或尾鳍(body and/or caudal fin, 简称BCF)游动模式以及中央鳍和/或对鳍(median and/or paired fin, 简称MPF)游动模式[1]。由于相对简单的设计和较高的推进性能，当前的仿生推进系统多采用BCF模式[2-3]，然而不少种类的鱼采用MPF模式进行姿态控制、提供辅助推进力等，以及在低速前进时直接将胸鳍作为主推进器[4]，海龟、企鹅等也使用类胸鳍的鳍状肢来推进身体向前游动。

有关仿生拍动翼(可看作胸鳍的一个简化模型)的研究发现，反卡门涡街为二维拍动翼尾流场的重要特征[5-6]，然而对于三维翼而言，其尾流场则由两个倾斜涡列所支配[7-8]。而胸鳍的形状和运动比三维翼更加复杂，胸鳍尾涡结构的关键特征究竟是什么还有待研究。

Suzuki等[9]开发了仿黑鲈鱼机械胸鳍推进系统，并开展实验研究工作，分析胸鳍的瞬时以及时均水动力特性。Li等[10]利用FLUENT软件及其动网格技术分析了胸鳍非定常运动尾流场中流向、展向系列切片上的涡的脱落和耗散过程。Lauder等[11]和Bozkurttas等[12]试验观测了太阳鱼稳定游动状态下的胸鳍几何和运动学数据，并进行与试验相匹配的数值模拟以提供详细的流场和水动力定量信息。陈宏等[13]建立了在胸鳍摆动模式下仿生机器人游动的物理模型，利用理论方法计算巡游时所受流体力，并进行数值仿真分析。Ramamurti等[14]对濑鱼胸鳍的游动行为进行数字化，并实施了相应的三维准定常和非定常胸鳍绕流数值研究。苏玉民等[15]开发了非定常涡格法程序，用行程时间比来模型化胸鳍的运动，计算分析了仿生胸鳍的推进性能。Hu[16]研究了在基于阻力的游动模式下胸鳍的水动力学问题，利用CFD计算给出了胸鳍的推力、推进效率和二维流场涡量分布。上述研究在仿生胸鳍的水动力性能预报和流场定量信息的获取方面取得了一些有价值的成果，但胸鳍三维尾涡结构的非定常演化过程还没有被深入地探讨，并且缺乏对胸鳍运动参数影响其水动力性能的机理的理解。

首先参考活体鱼胸鳍试验和运动学分析的有关文献进行仿生胸鳍计算模型的建立，然后通过与模型试验和其他数值方法的比较，验证所采用的数值方法模拟胸鳍绕流问题的精确性和可靠性，接下来研究仿生鳍瞬态运动过程中的尾涡结构演化与非定常水动力的关系，并探明支配胸鳍尾流场的关键涡结构，最后关注运动参数对仿生鳍的水动力性能和流场涡结构的影响，并根据研究成果对仿胸鳍推进系统的设计提出合理化建议。

1 胸鳍的计算模型

参考真实胸鳍的游动试验[17-18]，CFD计算中的仿生鳍几何模型如图1所示，其中鳍的最大弦长C为0.155 m，展弦比约为1.2，仿生鳍的尺寸约为试验中黑鲈鱼的胸鳍的6.2倍。

图1 仿生胸鳍的模型Fig. 1 Model of a bio-inspired pectoral fin

隆头鱼科模式鱼类胸鳍的典型游动模式有基于升力的游动模式和基于阻力的游动模式，其中前者由纵倾和上下拍动运动组成，而后者由纵倾和前后拍动运动组成[4]以及Kato[18]对黑鲈鱼胸鳍的观测和运动学分析，这种鱼的胸鳍可作为基于阻力的游动模式的典型。胸鳍的前后拍动运动可以表达为

φR(t)=φRC-φRAcos(2πf)

(1)

式中：φRA为前后拍动运动的幅值，φRC为前后拍动运动的平均值，f为运动频率，t为时间。

胸鳍的纵倾运动可由下式给出：

φFE(t)=φFEC-φFEAcos(2πf+ΔφFE)

(2)

式中：φFEA为纵倾运动的幅值，φFEC为纵倾运动的平均值，ΔφFE表示前后拍动与纵倾运动之间的相位差。图2中给出了在一个周期内胸鳍非定常运动的8个典型瞬时，为便于表明在胸鳍运动过程中鳍和鱼体的相对位置的变化，鱼体也被绘制出来以更清楚地显示胸鳍的运动情况(鱼体仅为显示目的并不包含在当前的数值计算中)。

图2 在一个周期内的胸鳍运动情况Fig. 2 Motion of the pectoral fin during one period

仿生拍动翼/鳍的研究中常用的无量纲参数，雷诺数(Re)和斯特劳哈尔数(St)，定义如下：

Re=UC/ν

(3)

式中：ν为流体的运动黏性系数。

St=fC/U

(4)

基于所建立的坐标系统，胸鳍的推力系数CT和升力系数CL可以表示为

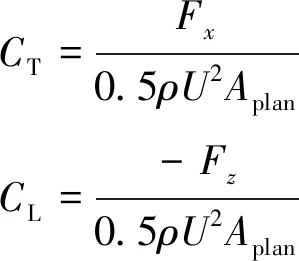
(5)

式中：ρ为流体密度，Fx为推力，-Fz表示升力(考虑到z轴向下)，Aplan为胸鳍的投影面积。对CT和CL分别在一个运动周期内取平均，有：

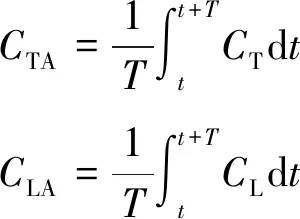
(6)

式中：CTA为平均推力系数，CLA为平均升力系数，T表示周期。

推进效率为胸鳍的平均输出功率Pout与平均输入功率Pin的比值，可用来流速度与平均推力的乘积来计算Pout，而Pin通过水对胸鳍做负功而被水吸收，最终得到计算胸鳍的推进效率的公式为

(7)

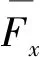
2 数值方法

鉴于在本研究中所应用的数值方法(一种浸入式边界方法)已在文献[19-21]中被详细阐述，这里仅对该方法的一些基本特征加以简要描述。控制胸鳍绕流问题的方程为非定常、不可压缩、三维Navier-Stokes方程：

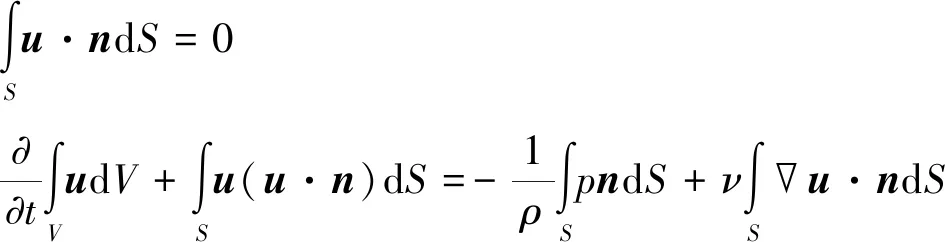
(8)

式中：u和p分别表示流体的速度和压力，ρ为流体的密度。采用有限体积法离散。一个分裂步方法(fractional-step method)[22]被用于压力速度耦合方程组的求解，流场网格划分形式为规则的六面体网格，物面网格划分形式为三角形网格。浸没边界对流体的影响通过引入虚拟单元(ghost-cell)来表示，这种方法的主要思想是利用流场的局部插值重构来满足物面的压力和速度边界条件。

3 结果与讨论

3.1 数值方法的验证

在文献[19-21]中，已通过若干算例对上述数值方法进行了广泛的验证，包括绕固定球体的流动、做大幅度运动的拍动翼和均匀流中圆柱体受迫振荡。本节针对所关注的仿生胸鳍水动力性能数值模拟，首先进行网格和计算域的无关性研究，然后将浸入边界法计算结果与试验结果和前人采用其他数值方法得到的结果进行比较，进一步验证本文数值方法的正确性。

数值计算中所采用的标准网格如图3所示。胸鳍表面由13 732个三角形网格离散；背景流场由693万个笛卡尔网格离散，为清晰显示流场中的网格分布细节，三个相互垂直的网格切片被给出；计算域(边界条件已在图中标出)的尺寸为10C(x)×4C(y)×6C(z)。在胸鳍附近的核心区域内以间距为0.008 6C的均匀网格提供极高的分辨率。在核心区域之外，网格向计算域的外边界迅速拉伸(对于近尾流区保证拉伸因子在3%以内)。网格无关性研究通过将胸鳍表面网格数和核心区域内3个坐标方向上的网格数加倍来实施，同时为保证整个网格系统的光滑性外部区域的网格数也做适当增加，细化后的流场网格总数为2 355万。计算域无关性研究是将计算域尺寸在3个坐标方向上扩大一倍来进行，在此过程中核心区域及其网格划分保持不变，而在外部区域使用与上述标准网格同样的拉伸因子。

图4给出了在数值计算中最后3个周期内(4T～7T)推力系数随时间的变化情况，此时流动已达周期性稳定状态(时间步长为T/400)。可以发现，在标准网格(nominal grid)、细网格(finer grid)和更大的计算域(larger domain)上计算得到的推力系数非常接近。因此，在接下来的模拟中采用标准网格，这样既能保证计算结果的精确性，也能使计算所需的时间和内存减少。

图5给出了在相同条件下的试验结果和各种数值方法的计算结果。经过7个运动周期的模拟流场已达周期性稳定状态，图中的是最后一个运动周期的模拟结果。总体来看，浸入边界法和Wang等[23]的试验结果，而苏玉民等[15]的势流理论方法由于没有考虑流体的黏性而与试验结果差距较大。进一步地对比可以发现，浸入边界法计算得到的CT随无量纲时间的变化曲线有与试验吻合较好的平缓波峰，而从FLUENT计算结果中则可看到较为尖锐的波峰。

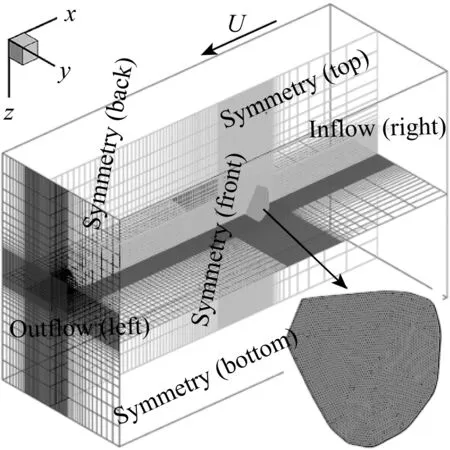
图3 计算域和网格分布Fig. 3 Computational domain and grid distribution

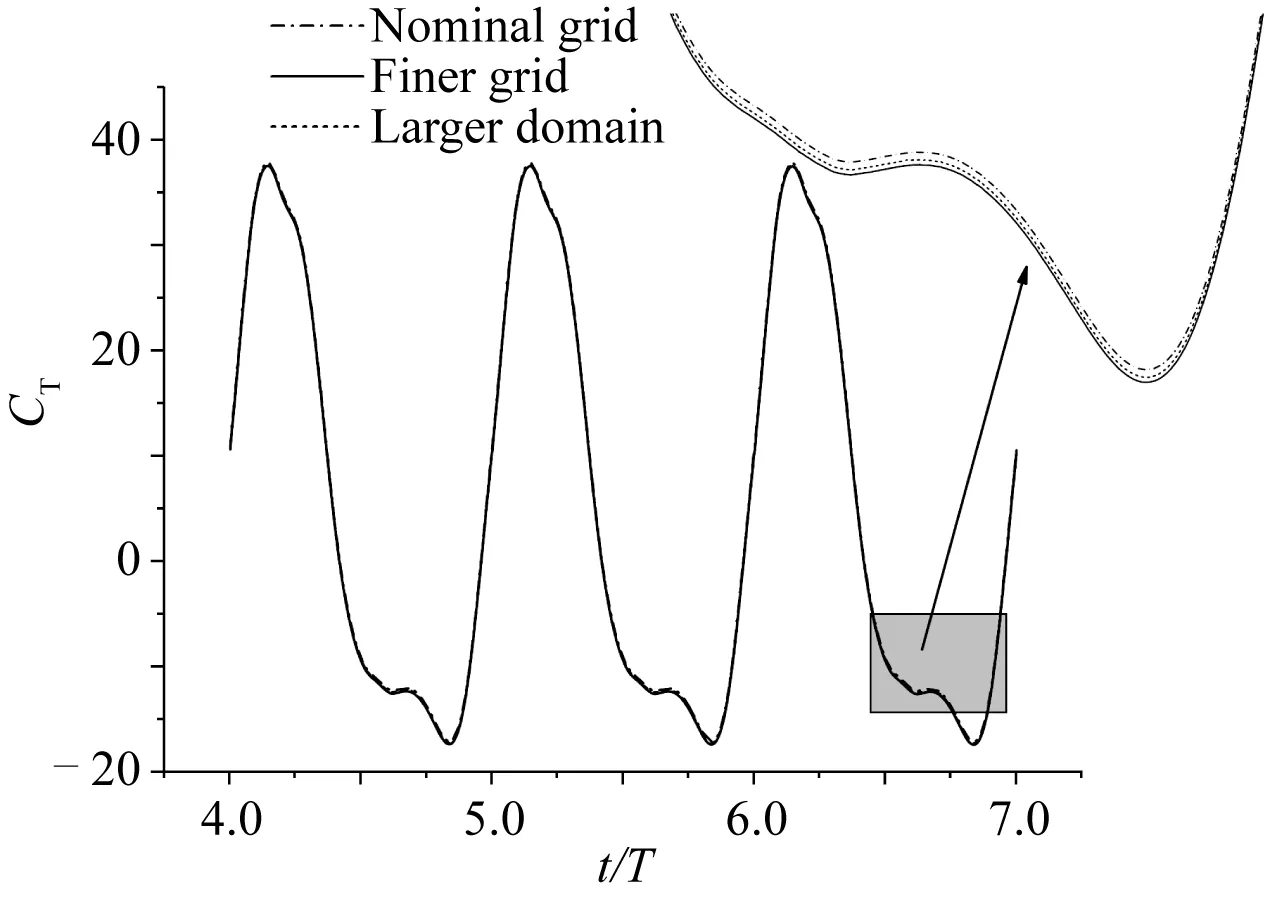
图4 不同网格和计算域下推力系数随时间的变化Fig. 4 Variation of thrust coefficient with time for different grids and computational domains

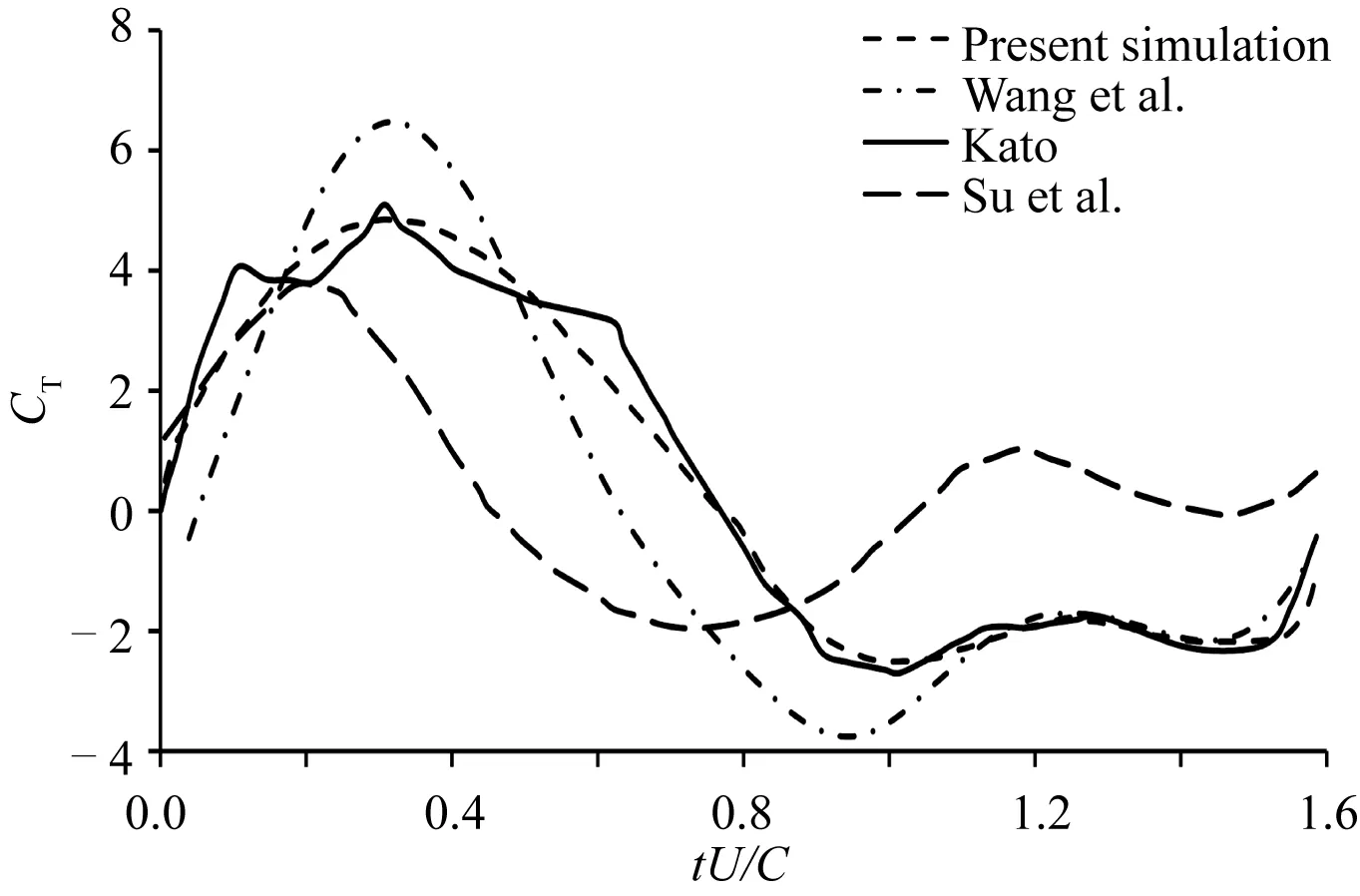
图5 推力系数数值与试验结果比较Fig. 5 Comparison of numerical and experimental results of thrust coefficient

3.2 胸鳍的非定常水动力和三维尾涡结构

3.2.1 推力系数和升力系数的脉动

图6给出了一个运动周期内胸鳍的水动力系数随时间的变化。其中雷诺数和斯特劳哈尔数的取值分别为Re=2 500和St=0.55，所选取的Re和St值均包含在Lauder和Jayne[17]的黑鲈鱼胸鳍试验所给出的无因次参数范围(1 756≤Re≤4 389和0.32≤St≤0.89)之内，还将在3.3节中对St的影响进行讨论。数值计算中其他的运动参数为φRC=30°，φFEC=-30°，φRA=30°，φFEA=30°，ΔφEF=90°，类似的参数取值已在有关胸鳍推进性能分析的有关文献[9, 18]中被采用。从图6中可以看到，胸鳍推力系数和升力系数曲线在每个运动周期均只有一个峰值。根据当前的计算，胸鳍在前半个周期主要产生推力，而在后半个周期主要产生升力。鉴于此在有关试验和数值研究[24]中，通常把胸鳍在一个周期内的划水过程分成两个阶段：动力划水(power stroke)阶段和恢复划水(recovery stroke)阶段。

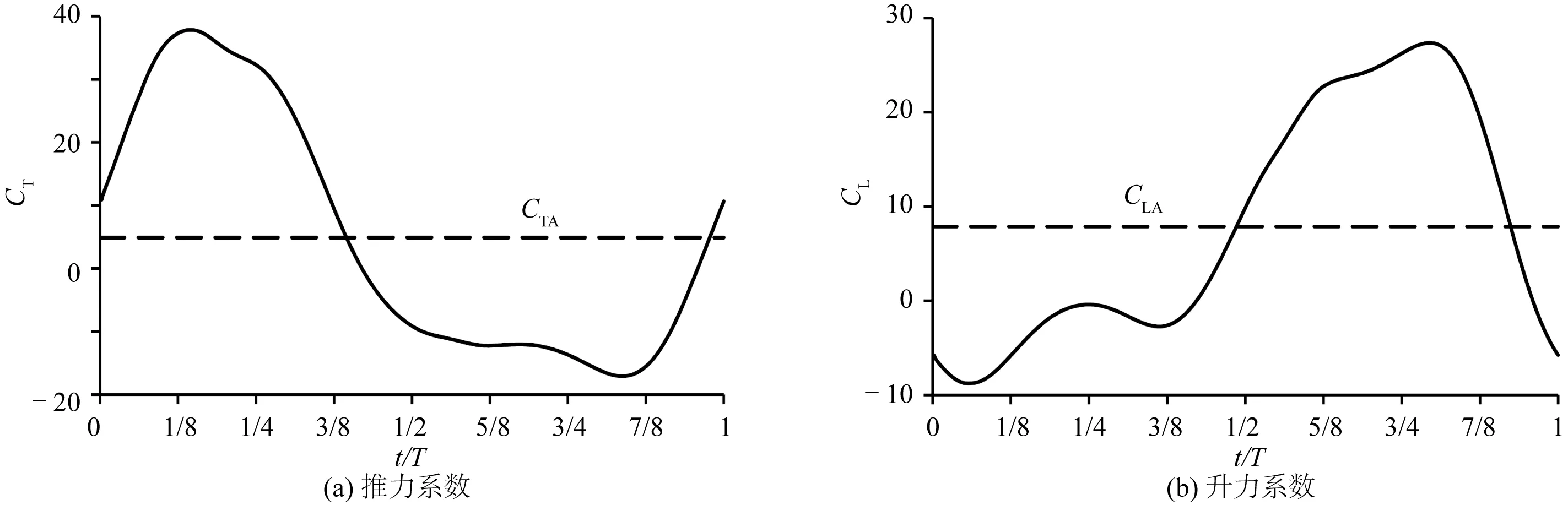
图6 水动力系数随时间的变化Fig. 6 Variation of hydrodynamic coefficients with time

3.2.2 尾涡结构与推进机理分析

一个周期内胸鳍运动的8个典型瞬时的三维尾涡结构(左图)、下游表面压力分布(中间图)和上游表面(迎流面)压力分布(右图)如图7所示。三维空间涡结构的识别采用Q判据[25]，左图中涡结构的颜色反映了涡量的大小，两侧表面压力分布图中胸鳍上的矢量为局部表面力。

1) 动力划水阶段

图7(a)给出了一个运动周期的初始时刻的情况。梢涡TV1、腹侧边缘涡VEV1和背侧边缘涡DEV1已从仿生鳍上脱落，尾流场中的两个涡环R1和R2为前面的两个运动周期所产生。

再来看1/8周期时的情况，如图7(b)所示，胸鳍上游表面有大片的低压力区出现，这是由附着在鳍边缘的马蹄形涡结构所诱导的，该涡结构的形成与胸鳍的快速向后摆动有关，它由新梢涡TV、新腹侧边缘涡VEV和新背侧边缘涡DEV连接而成。大片的低压力区意味着该运动瞬时仿生鳍的上游和下游表面之间有大压差力存在，而且该瞬时胸鳍表面和上游来流之间好的垂直度也有利于压差力在推力方向的分配，所以仿生鳍的推力在该瞬时几乎达到峰值(参考图6(a))。

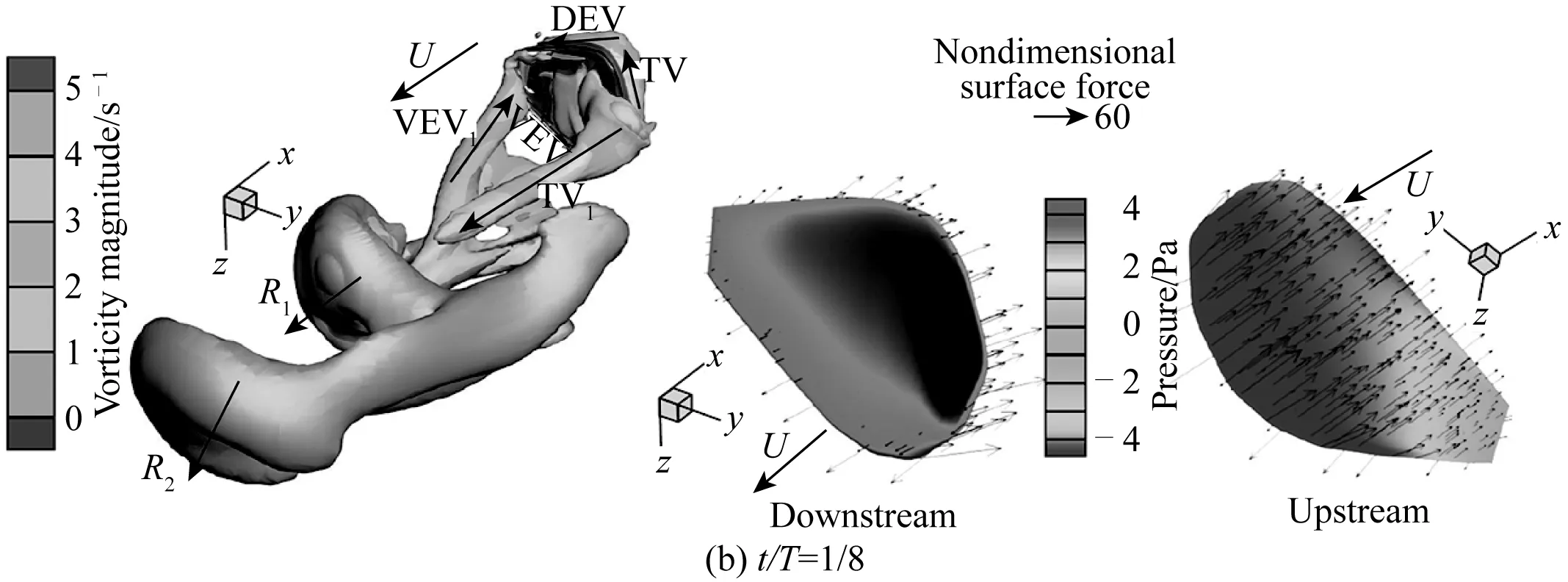
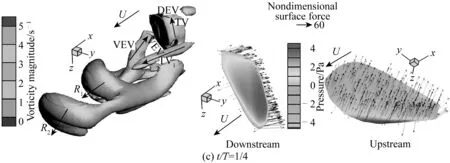
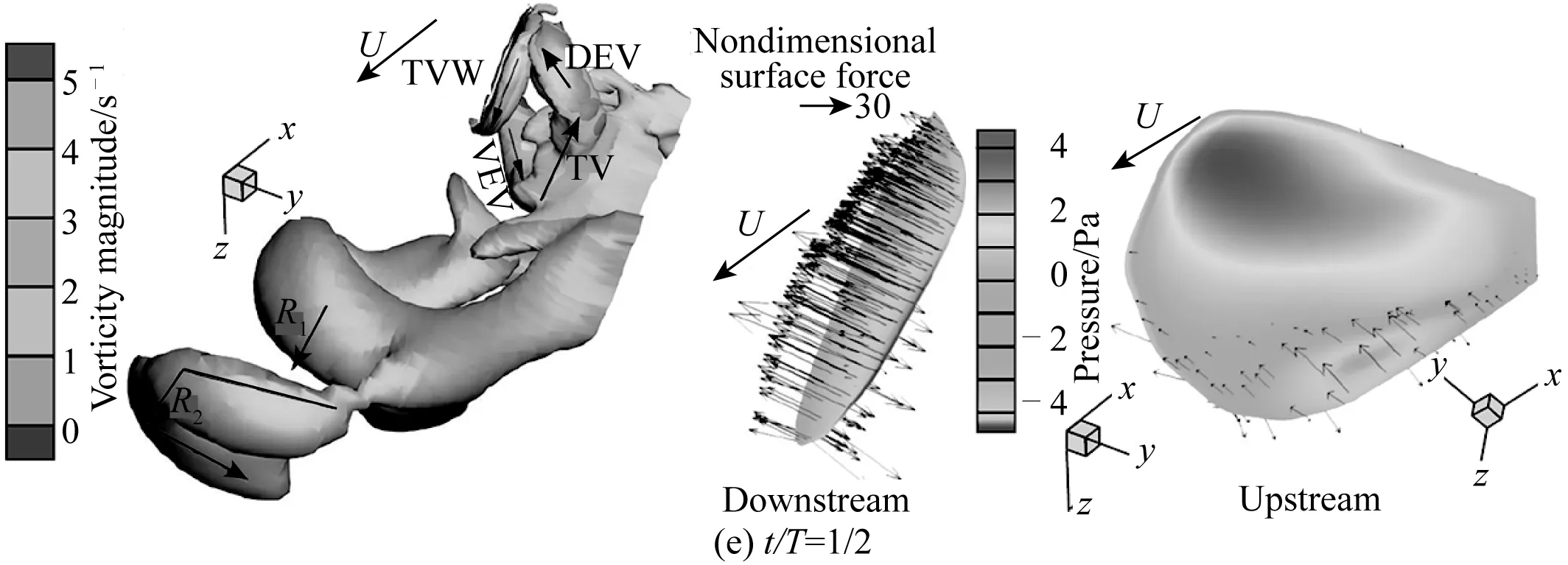
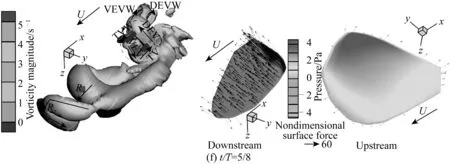
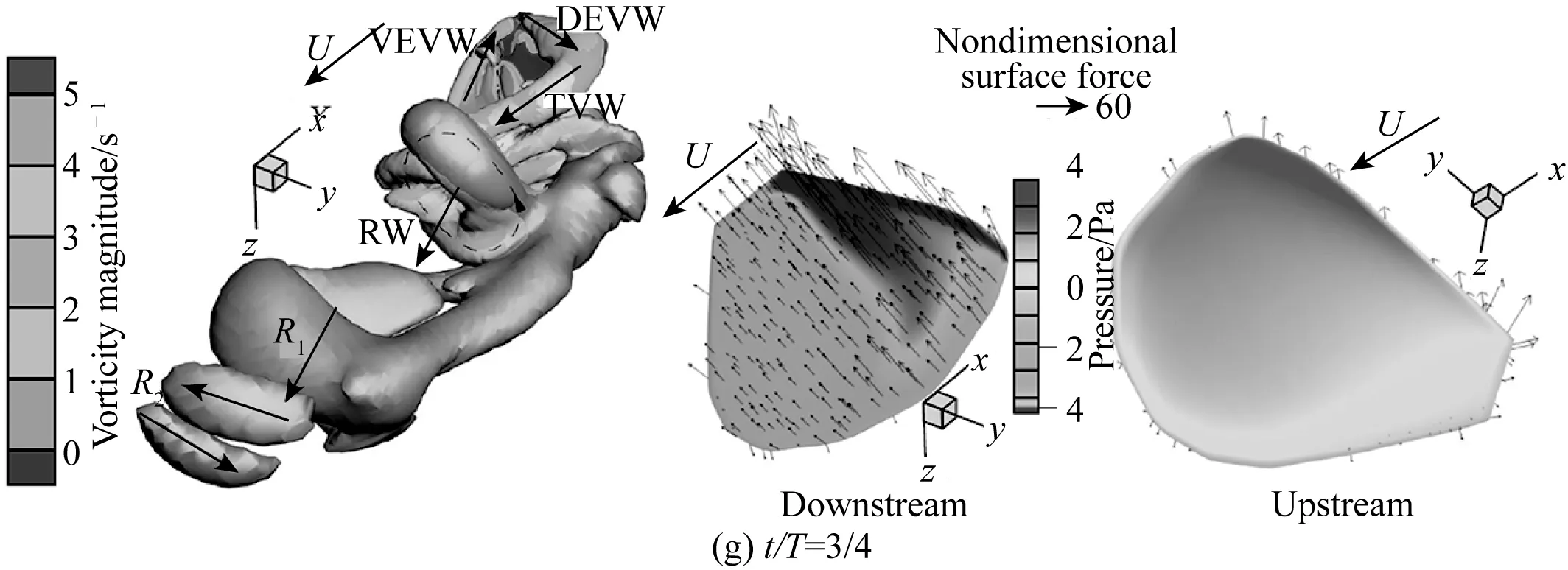
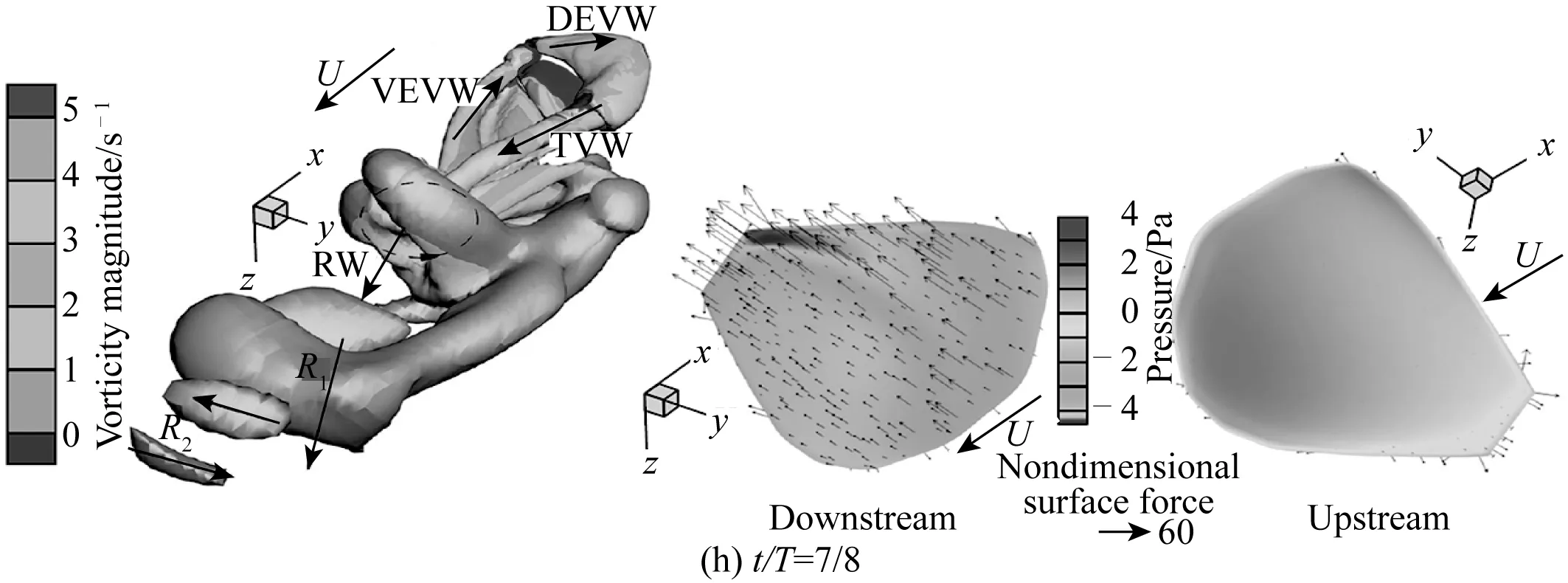
图7 典型瞬时的三维尾涡结构和鳍表面压力分布Fig. 7 Three-dimensional wake structure and pressure distribution on the fin surface at typical instants

图7(c)给出了1/4运动周期时的情况，可以看出，梢涡TV和背侧边缘涡DEV从鳍上脱落的过程已经开始，R1和R2两个涡环伴随着一定程度的耗散被尾流带向下游。

下一个运动相位(t/T=3/8)如图7(d)所示。TV连同部分的DEV和部分的VEV从胸鳍上脱落，这导致迎流面的低压区相比于前一时刻(t/T=1/4)继续减小。

2) 恢复划水阶段

在图7(e)中，即t/T=1/2的运动相位下，涡结构TV+VEV+DEV已经完全从胸鳍上脱落，鳍梢处又有新梢涡TVW正逐渐成长。

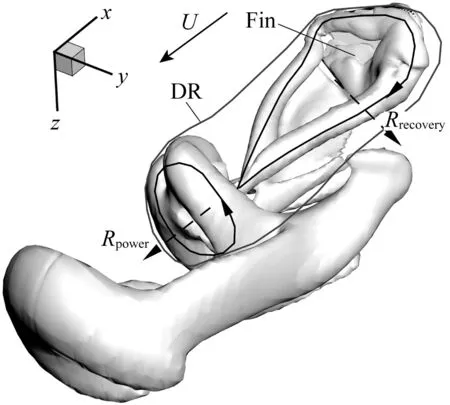
图8 胸鳍特有的三维双环涡Fig. 8 Particular three-dimensional dual-ring vortex for pectoral fin

t/T=5/8运动瞬时的情况如图7(f)所示，图7(e)中脱落的马蹄形涡与TVW相连而产生了一个新的涡环，胸鳍的腹侧边缘和背侧边缘又分别有新的附着涡VEVW和DEVW生成。

图7(g)给出了t/T=3/4时的尾涡结构和压力分布，新梢涡正在RW的诱导下被拉伸。仿生鳍向前摆动的同时，DEVW和VEVW上的涡量不断积累。在强大的DEVW的诱导下，一个显著的低压力区在胸鳍的背侧边缘附近出现，同时下游表面该区域存在较大压差力的事实也可从表面力矢量分布中看出，而且在这个运动相位时鳍面与升力轴之间的垂直度较好，导致被分解到升力方向的压差力比重增加。在上述这些因素的共同作用下，仿生鳍在3/4运动周期时的升力接近峰值(参考图6(b))。

图7(h)给出了7/8周期时的情况，此时仿生鳍在本周期的划水过程即将完成。TVW、VEVW和DEVW正在从鳍上逐步脱落，下一个运动周期的TV1、VEV1和DEV1(见图7(a))实际上正是从这些涡结构发展而来，同时RW这个涡环将发展成图7(a)尾流场中的涡环R1，这样下一个周期的仿生鳍运动和三维尾涡演变的循环即将开始。

3) 胸鳍尾涡结构的关键特征——三维双环涡结构。

以上关于推进机理的探讨事实上揭示出胸鳍三维尾涡的一个重要特征——双环涡结构，该特殊涡结构是由动力划水所生成涡环RW(R1)与恢复划水所生成涡环TVW+VEVW+DEVW (TV1+VEV1+DEV1)以接近垂直的角度相连而形成的。为使这一点变得更加清晰，绘制了图8，其中Rpower表示动力划水阶段所产生的涡环，它与恢复划水涡环Rrecovery一起构成了胸鳍独特的双环涡结构DR。

3.3 斯特劳哈尔数对水动力性能与尾涡结构的影响

对于仿生翼/鳍推进及鱼类游动来说，斯特劳哈尔数St是一个关键的无因次数，它特征化了流场涡结构和水动力性能[7]。就仿生翼及鱼类尾鳍而言，研究表明推进效率在St=0.3附近取得最大值[7, 26-27]。本小节分析St对胸鳍尾流场和推进性能的影响，及考查胸鳍推进的最优St。

1) 三维尾涡结构

在胸鳍一个划水动作的循环完成(t/T=1.0)时，不同St下的三维流场涡结构如图9所示，其他运动参数的取值与3.2节一致。能够观察到，胸鳍运动产生的尾涡随斯特劳哈尔数的增大而在涡强上有所增加，特别是对于胸鳍附近的涡结构(如TVW+VEVW+DEVW)而言。另外，模拟也发现在低St(0.25)时，前半个周期所生成的涡环RW与后半个周期所生成的涡环TVW+VEVW+DEVW分离。同时也可以看到，远尾流区的涡环取向随斯特劳哈尔数的增加而有所改变(即水平轴与涡环轴向间的夹角变小)，从而在涡环所引起的射流中流向动量成分的比例提升。

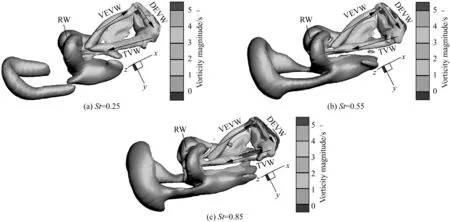
图9 尾涡结构随斯特劳哈尔数的变化Fig. 9 Variation of wake structure with Strouhal number

2) 水动力性能

St的改变对推力系数和效率的影响如图10所示。可以看出，胸鳍的平均推力随斯特劳哈尔数的增大而增加，这是由流场涡结构强度的增加和涡环的取向变化所导致的(见图9)，这两个因素造成与推力产生密切相关的射流的流向动量变大，进而引起推力的增加。

另一方面，效率随St的增加而先增大后减小。定量来看，效率先从22%(St=0.25)较快地提升到44%(St=0.55)，然后又较缓地降低到32%(St=0.85)。开始时效率随St的提升可解释为推力随斯特劳哈尔数的增大。达到最佳后效率随St的降低有以下两个原因: 1) 尾涡的强度增加(参考图9)使得更多的能量被尾流所携带； 2) 各涡结构之间的联系增多(参考图9)使得黏性抵消效应变得更显著，从而引起胸鳍向后射流动能的额外损耗。

以上数值模拟及分析表明：就胸鳍推进来说，也同样存在最优的St使效率最佳。本节的研究指出胸鳍的最优斯特劳哈尔数约为0.55，这与Lauder等[11]的试验得到的胸鳍进行常规游动时的斯特劳哈尔数的值0.54很接近。

图10 不同斯特劳哈尔数下的水动力性能Fig. 10 Hydrodynamic performance for different Strouhal numbers

3.4 相位差对水动力性能与尾涡结构的影响

1) 三维尾涡结构

在胸鳍一个划水动作的循环完成(t/T=1.0)时，不同St下的三维流场涡结构如图11所示，其他运动参数的取值与3.2节一致。不难发现，在所研究的相位差范围内胸鳍的尾涡结构是相似的，但ΔφFE=45°时的鳍梢部涡结构TVW相比于两个更高的相位差的情况更强。也可以看出，ΔφFE=45°时胸鳍的尾流宽而短，这种发散的尾流通常是低推力和效率的指示。在高相位差135°时，一个值得注意的现象是特殊柱状涡HV的出现，它由呈螺旋形的涡丝构成，在升力翼的尾流场中也出现了类似的螺旋形涡结构[28]，比较90°和135°时的平均升力模拟结果，发现后者比前者高了21%。Bozkurttas等[12]在胸鳍尾流场中也观察到了相似的螺旋形柱状涡。

图11 尾涡结构随相位差的变化Fig. 11 Variation of wake structure with phase angle

2) 水动力性能

图12给出了推力系数和效率随相位差的变化。当前的计算表明，在ΔφFE=90°时胸鳍同时取得最高的推进效率(44%)和平均推力系数(4.91)。当相位差以90°为标准值增加或减小时，均可以看到推力和效率的降低。具体地，相位差为135°和45°时的平均推力系数分别为3.57和2.23，推进效率分别为24%和15%。胸鳍在低相位差(45°)时产生较小的推力和效率与该相位差下的发散尾流(见图11)有关，而且从定量计算结果来看相位差以90°为中心上升和下降时所引起的胸鳍推进性能指标下降并不是对称的，胸鳍在高相位差(135°)时效率的降低与升力增加(相比90°时增加了21%)所导致的在垂向方向的能量损失增多有关。