钢靶分层厚度抗平头弹侵彻能力的影响规律研究

李小军，李 伟，谢长友，盖希强，王江波，高光发

(1 军事科学院防化研究院，北京 102205；2 南京理工大学机械工程学院，南京 210094)

0 引言

金属材料具有广泛的应用范围，同时也是军用防护材料使用最多的材料，45#钢是一种中碳优质结构钢，具有良好的综合力学性能。胡昌明等[1]、陈刚等[2-3]对45#钢进行一系列动静态力学试验，拟合了J-C本构模型的参数；王丽娟等[4]分析了45#钢高速冲击下的变形动态响应。

单层和多层靶板的抗侵彻性能已经引起研究者的注意，Radin等[5]对单层和多层铝靶抗钝头和锥形弹进行了一系列试验研究，发现抗侵彻性能随着分层降低，即单层靶的抗侵彻性能高于相同总厚度的多层靶。Teng等[6]使用ABAQUS建立了仿真模型，对单层和双层靶抗平头和锥头弹体的侵彻性能进行了研究，结果表明，分层结构提高了靶板对平头弹的抗侵彻性能。邓云飞等[7-8]等研究了单层板和接触式三层板对平头弹和卵形弹的抗侵彻性能，分析了靶体结构对靶体抗侵彻性能和失效模式的影响。Deng[9-11]等研究了层数、弹丸强度、层数间隙对钢板抗冲击的影响同时也对弹丸的穿孔行为进行了详细的分析。

文中在上述研究基础上，进行了长杆弹侵彻半无限靶板的仿真与试验对比研究，验证了材料参数的有效性和准确性，基于验证后的45#钢材料模型，利用ANSYS/LS-DYNA大型有限元软件，对靶板分层厚度与弹丸直径之比T/D抗平头弹的侵彻性能进行数值模拟，得到每种工况下的侵彻深度，分析了不同速度下靶板分层厚径比的最佳抗侵彻性能，为复合多层装甲的防护设计提供参考。

1 仿真计算模型

1.1 几何模型

弹体直径D为6 mm，长度L为60 mm，靶板直径为10D，即建立长径比(L/D)为10的平头长杆弹和直径为60 mm一系列不同厚度T的靶板。图1为不同T/D靶板的示意图。

图1 不同T/D的仿真几何模型示意图

当T/D=1时，图1中的T就为6 mm，总靶板由15个分层靶板组成。由于弹体、靶板及加载方向的对称性，建立了1/4的实体模型，采用8节点六面体单元和 Lagrangian算法，长杆弹和靶板的材料都为45#钢。在靶板的边界上施加固定约束，弹体与靶板、靶板之间采用单面侵蚀接触，关键字为CONTACT_ERODING_SINGLE_SURFACE，此接触算法的优点是计算时间快，特别适用于接触数量多、规律性研究的仿真计算。

1.2 材料模型

弹体和分层靶板均采用Johnson-Cook(J-C)模型，本构方程为:

(1)

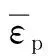
表1 弹丸和靶板45#钢材料主要参数

2 模型验证

利用25 mm口径轨道炮进行了弹芯直径为6 mm、弹长为90 mm的杆弹侵彻直径为80 mm、厚度为110 mm的45#钢靶板试验，采用高速摄影观察长杆弹的飞行姿态和着靶角度，并测量弹丸的飞行速度，图2为试验所用弹丸的结构图。

图2 脱壳穿甲弹结构图

图3 弹丸飞行过程高速摄像图

图3为长杆弹从发射到侵彻靶板过程中的高速摄像图，可以看出弹丸在整个飞行过程中飞行稳定，出炮口后弹托已经开始张开(图3中第1阶段)，经过一段距离的飞行，弹托已经分离(图3中第3阶段)，但由于靶板距炮口只有2 m的距离，导致弹芯和弹托并不能完全分离，但这并不影响弹芯的侵彻；在侵彻靶板时弹丸着靶角为0°，即弹丸垂直侵彻靶板(图3中第4阶段)。

利用LS-DYNA仿真软件建立与试验条件相同的1/4仿真模型，并在对称面上施加对称约束，靶板的侧边施加固定约束，模拟靶板被固定的条件。图4为杆弹速度为1 516.2 m/s时靶板的侵彻试验和仿真结果对比图，从图中可以看出，试验侵彻深度与仿真结果对比较好，且弹坑形状也相同，但初始的弹坑直径不同，这是由于仿真模型中没有考虑弹丸的圆锥尾翼。

图4 速度为1 516.2 m/s时试验与仿真对比图

图5为不同速度V杆弹侵彻靶板侵彻深度P的试验与仿真数据对比图，从图中可以看出，试验侵彻深度与仿真绝大多数相差在2%以内，值得注意的是当速度为1 316.9 m/s时，仿真与试验侵彻深度相差7.2%。

图5 不同速度杆弹侵彻靶板仿真试验侵彻深度图

根据图4和图5，发现试验弹坑和数值模拟弹坑基本一致，试验侵彻深度和数值模拟侵彻深度相差较小，并且随着速度的增加，两者侵彻深度的增加具有很好的一致性，验证了仿真模型和材料参数的有效性和准确性，同时说明数值仿真模型能够准确的描述长杆弹侵彻试验。

3 仿真结果分析与讨论

图6为T/D=1的靶体分层厚度在不同速度下侵彻后剩余的弹体图，由于靶板的可变形性和杆弹在侵彻过程中的塑性流动变形导致杆弹侵彻端面出现外翻现象，呈现蘑菇头形状，值得注意的是，随着速度的增大，杆弹的剩余弹体也越来越少，杆弹头部外翻的也越多。

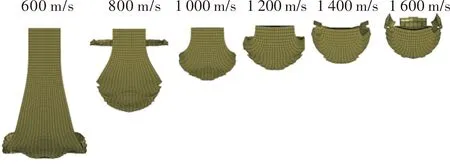
图6 不同速度杆弹侵彻T/D=1靶后剩余弹体

图7为杆弹以1 600 m/s的速度撞击T/D=1靶体结构的典型过程图，分别截取了杆弹穿过每层靶板的Mises应力云图，从图中可以看出，靶体的变形主要是局部变形，整体靶板的变形很小，当靶板穿过第1层靶板时，第2块靶板已经发生了塑性流动，靶板的正面已经出现凹坑，背面有鼓起的部分，但由于后续靶板的作用力，导致凸起部分不太明显；当弹丸完全侵彻贯穿1层靶板时，靶板中间向上隆起，第1层最为明显，后续隆起高度逐渐变小。

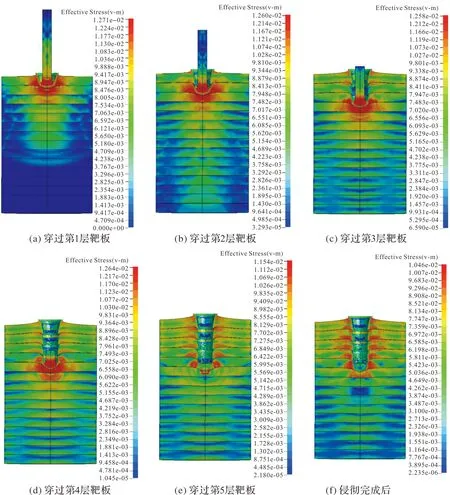
图7 靶体T/D=1时的典型侵彻过程

图8为不同速度杆弹侵彻靶体厚径比为T/D=1时的速度和加速度时程曲线，由图8可以看出，侵彻速度越大，侵彻停止的时间越快，侵彻过程中的最大加速度也较大;当杆弹速度为600 m/s时，杆弹的加速度近似于一个定值，当速度大于800 m/s时，弹丸的速度和加速度历程具有一定的相似性。

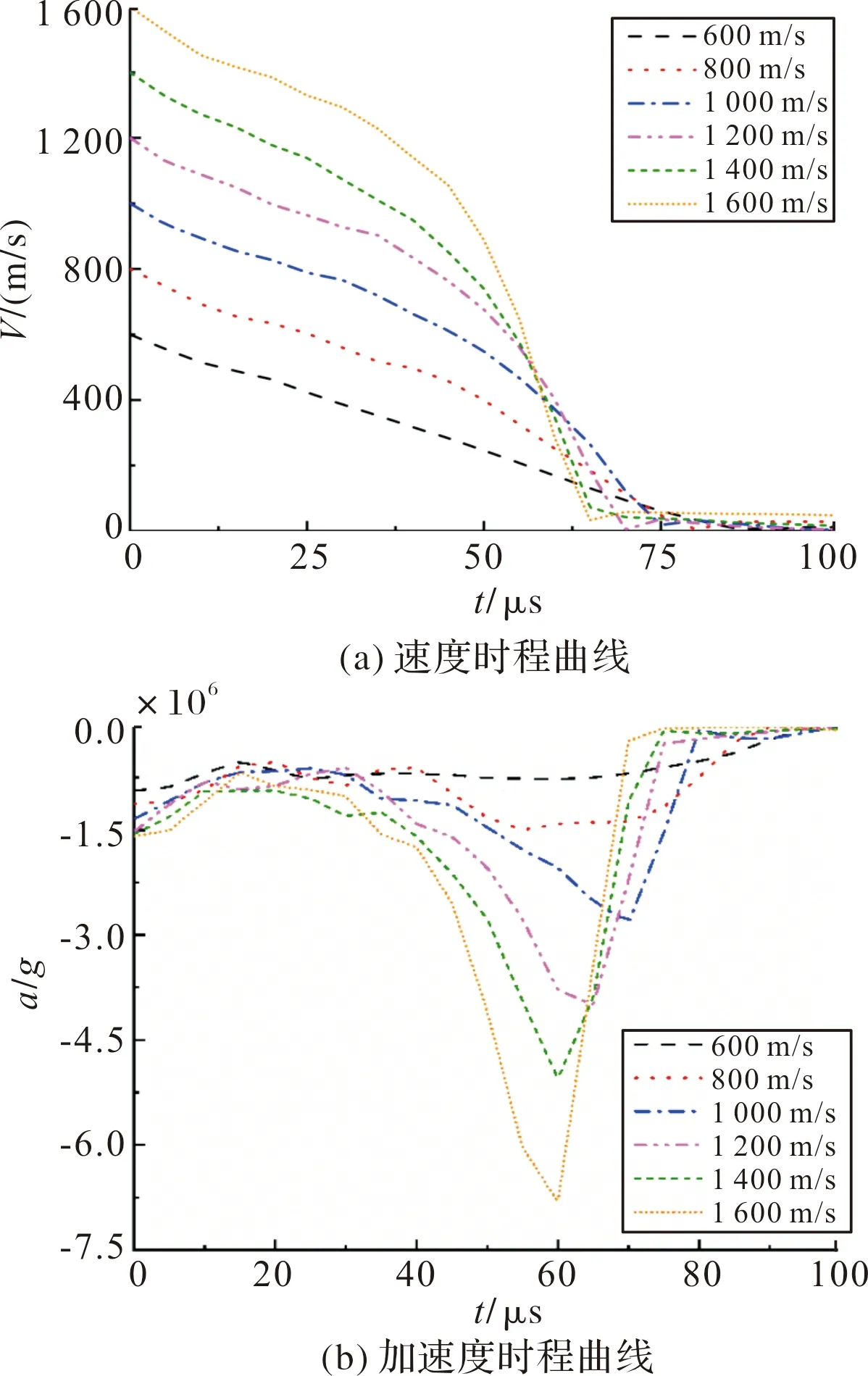
图8 靶体结构T/D=1时侵彻速度和加速度曲线

图9为长杆弹侵彻T/D分别为0.5，0.75，1，2，3，4，5，6，7，10分层靶板的侵彻深度曲线，从图中可以看出，随着速度的增加，每种分层靶板的侵彻深度都随之增大，且增加趋势具有一致性；在速度低于1 000 m/s时，所有分层靶板的侵彻深度随速度的增加较慢，而速度在1 000～1 600 m/s时，侵彻深度随杆弹速度的增加增大较快，趋于直线增加；在低速情况下，所有分层靶板的抗侵彻性能相差不大，但在速度大于1 200 m/s时，靶板分层T/D(≤1)的值越小，侵彻效率越高。

图9 不同T/D靶板的速度与侵彻深度曲线

为了更直观地观察靶板不同分层的抗侵彻性能，图10给出了靶板分层厚径比与侵彻深度在不同速度下杆弹侵彻的深度，由图可以看出，在速度为600 m/s,800 m/s和1 000 m/s时，不同分层靶板的抗侵彻能力相差不大，但存在一个最小侵彻深度分层厚径比，即T/D=6时，杆弹的侵彻深度最小，靶板的抗侵彻效率最高；当速度为1 200 m/s,1 400 m/s和1 600 m/s，T/D<1时，侵彻深度急剧增加，分别增加了9%,11.7%和5%，同样存在一个最小的侵彻深度分层厚径比，即在T/D=5时侵彻深度最小，即靶板的抗侵彻性能最好，值得说明的是，速度为1 400 m/s时，侵彻深度最小的是T/D=7，但与T/D=5时的侵彻深度相差为0.75%，可以认为最佳抗侵彻分层厚径比为T/D=5。

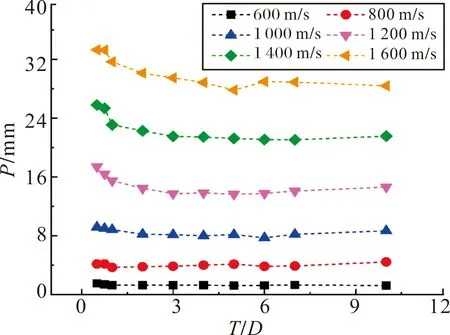
图10 分层结构T/D与侵彻深度的关系图

4 结论

研究了不同分层靶板厚径比对直径为6 mm、长径比为10的长杆弹的抗侵彻性能，分析了靶体的最佳抗侵彻分层厚径比，得到以下结论：

1)进行对比试验，证明采用合适的材料模型进行仿真可以有效的研究靶板的抗侵彻性能。

2)对每种厚径比分层靶板进行了不同速度下的抗侵彻数值模拟，仿真结果表明：当速度在600～1 000 m/s范围内，抗侵彻性能最好的靶板分层厚径比为T/D=6，当速度高于1 000 m/s时，最佳靶板分层厚径比为T/D=5。

3)分析靶体分层T/D=1时的速度和加速度时程曲线，发现速度越高，杆弹侵彻过程中最大加速度越大，侵彻完成的时间越短。

此外，由于金属材料具有严格的几何相似率，文中研究的是45#钢杆弹侵彻45#钢分层靶板的抗侵彻规律，故得到的结论可以对其他口径的杆弹抗侵彻研究具有一定的参考意义。