五边形格点的几何阻挫和热力学性质

朱敏敏，杨 丽，廖艳华

(湖北理工学院 数理学院，湖北 黄石 435003)

在过去的60年里，研究者们在用晶格模型来确定物质相变点附近的临界行为方面做了很多工作，使人们更深入地理解了磁性固体中的有序和无序现象。自从 Onsager开拓性地提出晶格的二维伊辛模型[1]的精确解求解方法以来，利用推广的Onsager方法陆续地得到了其他二维晶格模型的精确解[2]，如三角形蜂窝状晶格[3-5]以及正方形二维模型[6-7]。

在三角形格点的相关研究中，几何阻挫问题不可回避[8]，其主要基于三角形和四面体结构。但Waldor等[9]结合伊辛模型指出，类似Penrose图案的五边形晶格里也存在阻挫现象，并利用传递矩阵法精确地求出了该模型的解析解。此外，Rousochatzakis等[10]在Cairo的伊辛模型帮助下，对五边形格点进行了研究，讨论了临界温度和自发磁化强度等性质。

近年来，研究者们发现反铁磁材料Bi2Fe4O9中的Fe3+晶格具有五边形晶格结构。Singh等[11]利用五边形海森堡模型对其进行了讨论，发现这种材料具有明显的阻挫现象。同时，利用晶格动力学方法对Bi2Fe4O9中的声子结构进行理论模拟，研究结果也表明其结构中存在阻挫。此外，Bi2Fe4O9的偏振拉曼光谱实验也证实该材料在10～300 K时会出现阻挫现象[12-13]。Isoda等[14]也通过推广的玻色子Hubbard模型，使用数值量子随机级数展开与蒙特卡罗方法对五边形晶格进行了理论研究，但采用伊辛模型研究有限格点的量子现象，还鲜有讨论。

本文利用伊辛模型，通过建立热力学配分函数，研究磁场和格点间的交换强度对磁矩、自旋关联函数和熵的影响，旨在为具有五边形格点的准晶的微观状态研究提供帮助。

1 建模与计算

利用伊辛模型对正三角形和正方形构成的五边形格点进行建模，并通过热力学函数来研究该格点间的量子磁化机制。由正三角形和正方形构成的五边形格点模型示意图如图1所示，其中，圆圈处代表具有自旋的格点。假设该格点受到沿Z轴方向的外加磁场B的作用，则每个格点的自旋在Z轴方向上的投影有2个方向，分别是向上(+)或向下(-)，大小均为1/2。

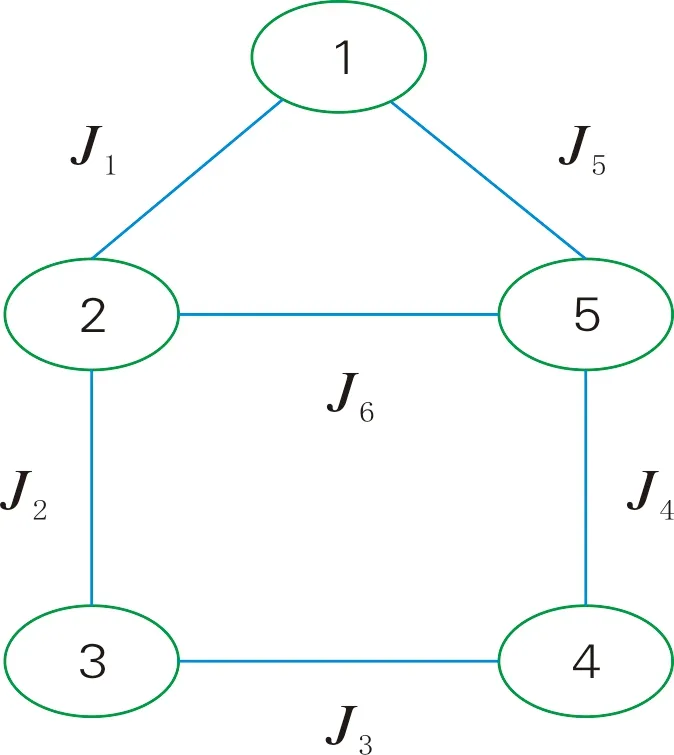
图1 由正三角形和正方形构成的五边形格点模型示意图

伊辛模型下，图1五边形格点的哈密顿量可表示为：

H=J1SZ(1)SZ(2)+J2SZ(2)SZ(3)+J3SZ(3)SZ(4)+J4SZ(4)SZ(5)+J5SZ(5)SZ(1)-B[SZ(1)+SZ(2)+SZ(3)+SZ(4)+SZ(5)]

(1)

根据式(1)中的哈密顿量，结合伊辛模型特点，考虑最近邻格点间的相互作用，有J1=J2=J3=J4=J5=J,系统的能量本征值由五边形格点32种自旋组合模式给出：

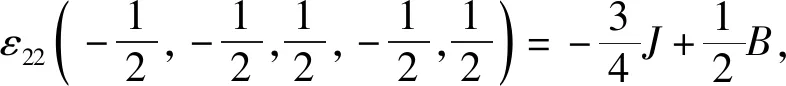
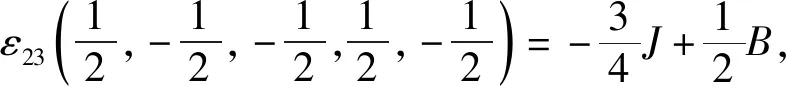
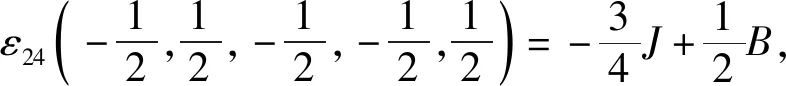
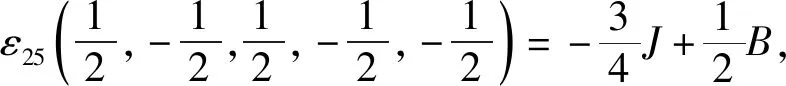
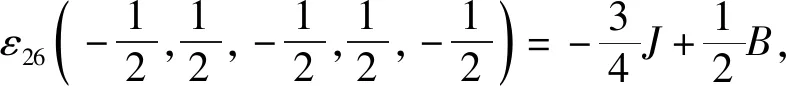
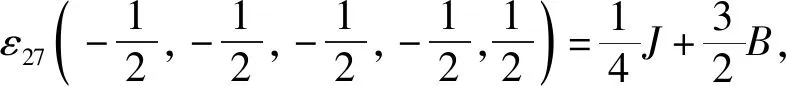
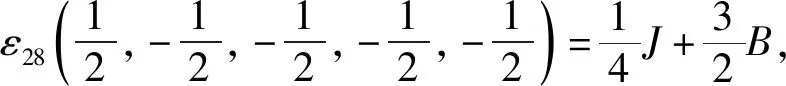
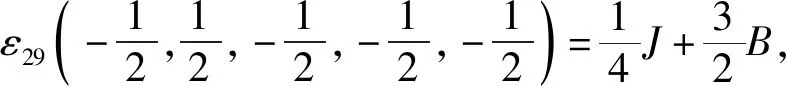
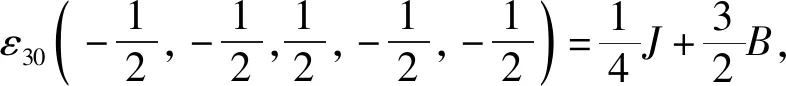
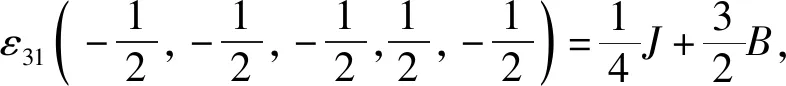
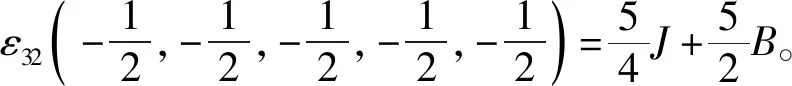
根据能量本征值，系统配分函数为：

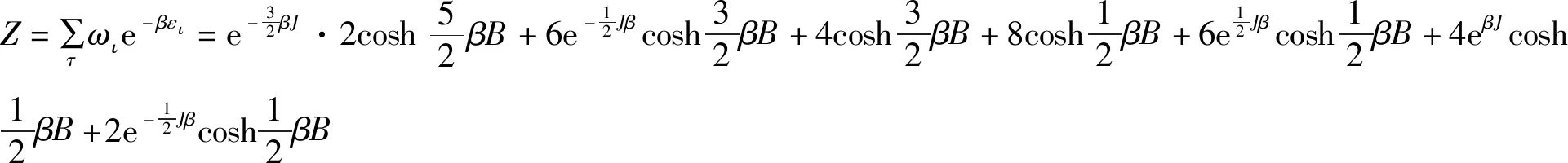
(2)

根据磁矩与配分函数的关系，可得磁矩与外加磁场和格点间交换强度关系为：

(3)

格点间自旋关联函数为：

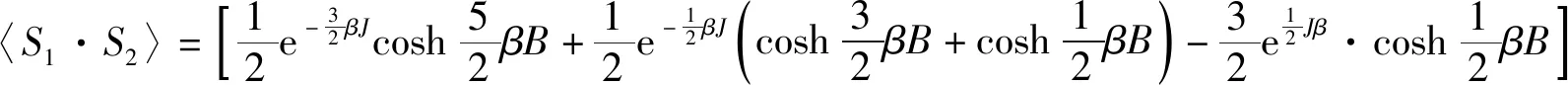
(4)

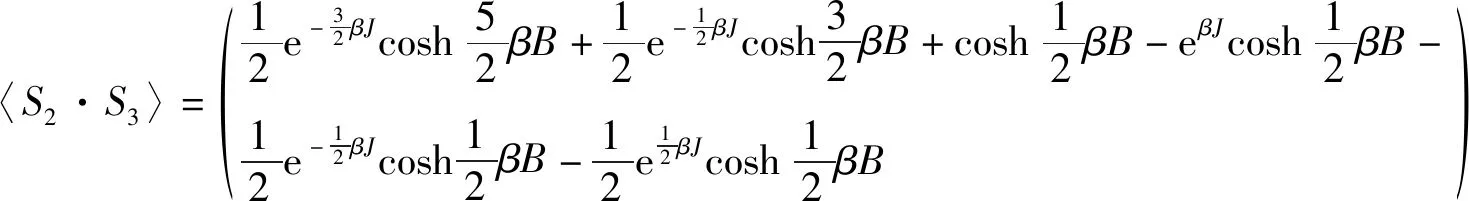
(5)

系统的热力学熵为：

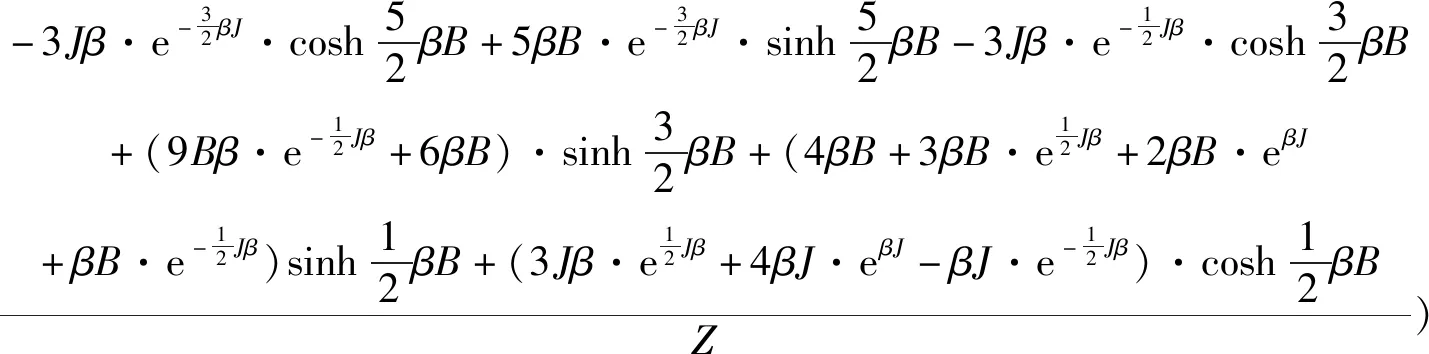
(6)

式(6)中，Ω为状态数；k为玻尔兹曼常数。

2 五边形格点间的自旋关联与磁化过程的微观机制

2.1 五边形格点磁化过程

根据式 (2)～(6)，绘制出五边形格点的磁矩、热力学熵和自旋关联分别随交换强度与磁场强度的变化曲线如图2～9所示。由图2可以看出，对于一定的磁场强度(如B/kT=5), 随着交换强度J/kT由负值变为正值，磁矩M越来越小。

曲线的变化态势说明五边形格点间的自旋关联由铁磁态过渡到反铁磁态，最终磁矩变为一个电子的剩余磁矩，且为正值，此时自旋方向和磁场方向保持一致。这一变化过程也表明，当交换强度为负值时，系统偏向于铁磁关联；交换强度为正值时，系统偏向于反铁磁关联。由图2还可以看出，当磁场很小时，如B/kT=1时，系统的最大磁矩接近2.5，表明此时的交换强度和磁场使得五边形中格点的自旋都指向Z轴的正方向。当交换强度足够大时，磁矩最终会接近至0.25左右，而不是0.5，这表明格点中存在阻挫，系统是一个量子混合态。随着磁场增大，如B/kT=10时, 系统的最大磁矩为2.5，说明此时磁矩趋于饱和，5个格点的自旋方向一致；而此时的最小磁矩接近0.5，表明磁场能消除部分交换强度对格点形成的反铁磁的影响，展现了磁场与交换强度的一个竞争机制。特别地，我们绘制了B/kT=0的曲线，此时磁矩为0。这是由于在没有外加磁场下，交换强度会使格点之间形成反铁磁关联，但格点的自旋方向是随机的，所以总磁矩为0。

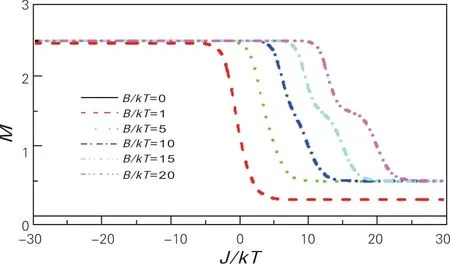
图2 不同磁场强度下，磁矩随交换强度的变化曲线

由图3可以看出，当磁场足够大时，五边形格点中的自旋均会朝向磁场方向，完全被磁化，所以曲线中总磁矩最大值为2.5。当晶格之间交换强度较小时，如J/kT=1时，随着磁场强度正向增大，磁矩快速变化，表明格点会被迅速磁化；随着交换强度变大，如J/kT=15时，磁矩变化速度放缓。从图3也能观察到曲线都通过坐标(0,0)点，且关于该点对称。这是因为当磁场为0时，每个格点的自旋方向是随机的，自旋的方向在某一方向上都不比其他方向有优势，从统计学角度来看，各个方向的概率相同，故而宏观体现出来的是0。同时，随着交换强度变大，如J/kT=5，10，15时，在M=0.5处会出现台阶，且台阶的宽度会随着交换强度的增强而变宽，这是由磁场与交换强度的竞争所导致。磁矩为0.5的情况，可以通过图4和图5进行解释。

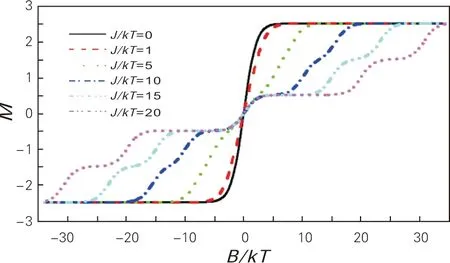
图3 不同交换强度下，磁矩随磁场强度的变化曲线

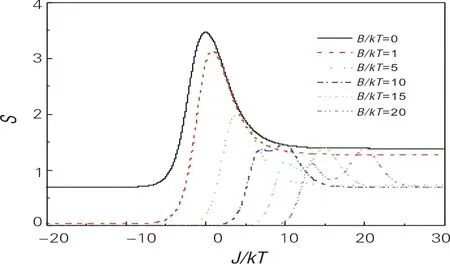
图4 不同磁场强度下，熵随交换强度的变化曲线

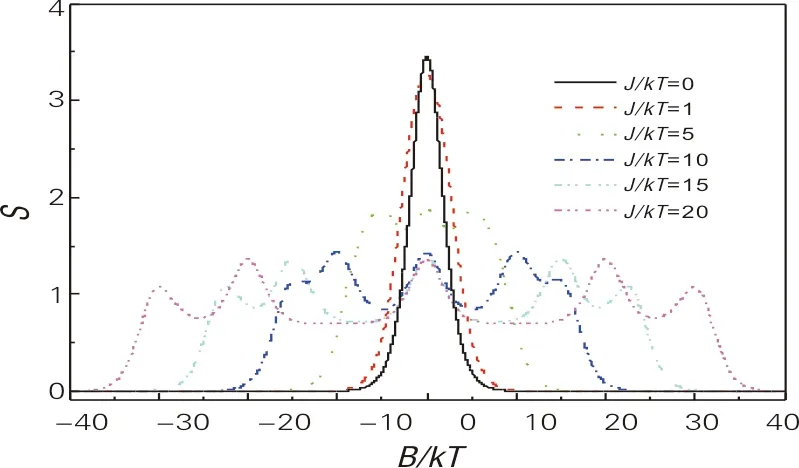
图5 不同交换强度下，熵随磁场强度的变化曲线

图4和图5描绘的是一定磁场(交换)强度下熵随交换(磁场)强度的变化情况。利用公式(6)可以观察系统对应的状态数，运算时取k=1。由图4可以看出，对应一定的磁场强度，当交换强度为负值时，系统微观状态为0。这是由于当存在正向磁场和负的交换强度时，五边形格点间存在纯粹的铁磁关联，格点的自旋状态只有一个；随着负的交换强度减小，格点间的铁磁关联减弱，五边形各格点自旋方向状态数增多，熵变大。此外，随着磁场强度增大，峰值会随着交换强度的增加而右移，表明交换强度与磁场存在竞争。从图5可以看出，熵图呈现了左右对称性，这一特性也反映出图3中磁矩关于原点对称的情况。这里需要特别指出的是，对于图4和图5，当J/kT=0，B/kT=0时，五边形总的状态个数是32个，这是由于在没有交换强度和磁场影响下，每个格点自旋有向上或向下2种情况，5个格点自旋的组合个数就是32种。随着交换强度增加，格点间形成的铁磁关联越来越强，所以状态数会越来越少，在B/kT=0处的峰高会越来越低。这里我们也注意到，对应一定的交换强度，如J/kT=15时，系统的状态数会随着磁场强度的变化出现振荡，这是由于系统在磁场增大过程中，交换强度与磁场的竞争导致状态数变化；而对于交换强度没有或较小时，如J/kT=1时，由于交换强度不足以和磁场竞争，随着磁场增大，五边形格点的自旋会被快速磁化，向磁场方向偏转，不会出现振荡现象。

2.2 五边形格点间的关联

五边形1，2格点和2，3格点之间的自旋关联随交换强度和磁场强度的变化曲线如图6～9所示。由图6可以看出，当交换强度为负值时，由于其作用效果和正向磁场都会使格点自旋方向与磁场保持一致，此时会出现铁磁关联，所以关联度为0.5×0.5=0.25。随着交换强度减小，铁磁关联随之减小。当交换强度为正值时，1与2格点间呈现反铁磁关联，同时，即使在B/kT=0时，即没有外加磁场时，较大的交换强度也不能使五边形格点间达到完全的反铁磁关联值-0.25，这是由阻挫所导致。这一现象可以通过比较图6和图7获得验证。同为全同格点，1与2的关联和2与3的关联应该相同，但实际情况是这2种关联在交换强度为负值时相同，但在交换强度取正值时出现不同，这与文献[15]讨论的三角形阻挫情况类似。根据能量越低越稳定的特点，系统的哈密顿量趋向能量最低，即反铁磁关联。但由于存在阻挫，2，3格点无法与1格点同时形成反铁磁关联，当2，3格点形成反铁磁关联时，1与2格点反而存在一定几率的铁磁关联(没有达到完全铁磁或反铁磁关联度0.25)。这些现象都表明系统存在铁磁与反铁磁的混合态。

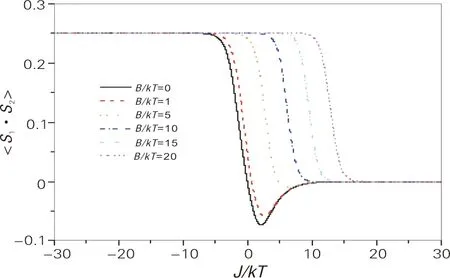
图6 不同磁场强度下，1与2格点间的自旋关联随交换强度的变化曲线

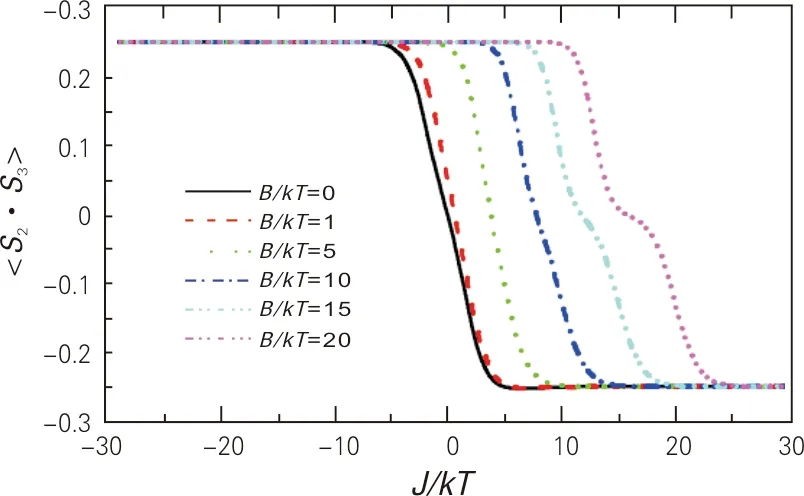
图7 不同磁场强度下，2与3格点间的自旋关联随交换强度的变化曲线

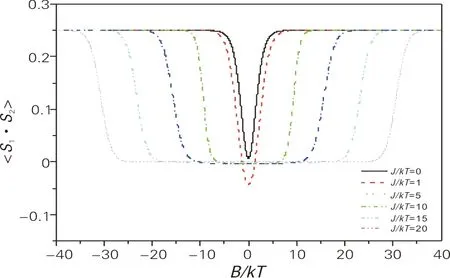
图8 不同交换强度下，1与2格点间的自旋关联随磁场强度的变化曲线

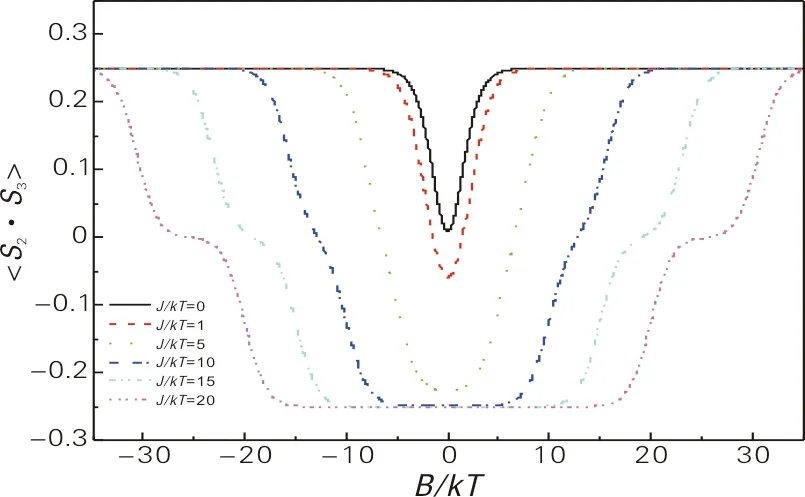
图9 不同交换强度下，2与3格点间的自旋关联随磁场强度的变化曲线

3 结论

利用伊辛模型对由正三角形与正方形构成的五边形格点的晶格进行了理论研究。在热力学配分函数的帮助下，通过研究格点间的磁化强度、自旋关联函数和热力学熵，得出了五边形磁化的微观机制，指出五边形格点中会存在类似正三角形格点中的阻挫现象。同时，五边形格点在磁化过程中呈现的磁化台阶与三角形个数不相同，且熵值出现振荡，表明系统的微观态会随着磁场或交换强度的变化而变化。由于格点数增加后微观态数会相应变多，五边形格点的磁化过程中的微观态较为复杂。研究结果表明，通过有限格点的伊辛模型精确求解，所得出的五边形磁化规律结论与采用数值方法获得的无限格点的结论一致[14，16]。