路面结构S型复合土工材料排水系统性能分析

刘毓氚， 张川

(福州大学土木工程学院， 福建 福州 350108)

0 引言

路面结构中水分的增加将会显著引起土体结构弹性模量降低[1]， 增加车辙深度. 为缓解水对路面结构造成的不利影响， 通常在路面结构中设置适当的排水结构[2]， 如在路肩侧设置排水沟, 在基层与路基之间设置碎石排水层或铺设土工织物. 传统的排水措施仅限于排除土体饱和条件下水分， 而无法排除非饱和条件下积水. 非饱和条件， 即土体孔隙中不含水或所含水的体积未充满整个孔隙. 根据非饱和渗流原理[3]， 此时土体中具有较高的基质吸力， 土体的渗透率随着基质吸力增大而急剧下降， 并且粗颗粒土体的渗透率比细颗粒土体下降的更快[4]. 因此， 非饱和条件下采用在基层下方铺设碎石排水层或土工织物的传统排水措施， 将会在接触面处形成毛细屏障阻挡基层中的水分下渗到排水层. 水在基层中积聚导致基质吸力降低， 当基质吸力降低到“突破吸力”值时， 基层土体的渗透率等于排水层材料， 此时水分才会进入排水层被排出路面结构. “突破吸力”到来的时间越短， 意味着排水系统开始排水的时间越早， 则上层土体中就能保持较大基质吸力.

众多学者对解除路面结构的中毛细屏障展开了研究. 美国FIT公司研发一种芯吸纤维土工织物[4]， 该种芯吸纤维采用亲水性材料结合纤维表面较深的沟槽大大增强了土工织物在非饱和条件下排水的能力， Zornberga等[5-6]开展的室内试验也证明该种芯吸纤维土工织物具备非饱和条件下排水的能力. Stormont等[7-9]提出复合土工合成材料排水系统(GCBD)理论， 该排水系统由水力传导层、 防渗层和隔离层组成. Stormont等在研究中采用玻璃纤维土工织物作为水力传导层， 能够实现非饱和条件下排水， 但由于玻璃纤维在制造业中应用少， 制成的土工织物成本较高.

本文在GCBD理论的基础上， 提出以亲水性材料制成的非编织土工织物为水力传导层和隔离层、 S型排水板为防渗层组成复合土工合成材料新型路面结构排水系统. 该排水系统理论上兼有在非饱和条件下排水和防止水分入渗到路基的性能， 但在实际应用中效果尚不明确， 并且水力传导层土工织物各参数在何值时能发挥最大解除毛细屏障的能力尚待研究. 为此， 首先开展室内模型实验， 通过在人工降雨条件下监测基层和路基土体的基质吸力和体积含水量变化来反映新型路面结构排水系统的效能， 其次通过数值模拟验证模型的准确性， 最后分析土工织物Van Genuchten参数a值、 饱和渗透率和厚度取不同值时其排水性能的变化， 并为各参数建议取值范围.

1 S型复合土工材料路面结构排水系统

S型复合土工材料路面结构排水系统由水力传导层、 防渗层(S型排水板)和隔离层组成， 如图1所示. 该系统以非饱和土渗流原理为依据， 目的是实现路面结构在非饱和条件下排出入渗水分.

S型复合土工材料排水系统组成形式如图2所示， 水力传导层和隔离层采用的是亲水性材料制成的非织造土工织物[10]， 由于该种土工织物具有大于传统碎石排水层的水力传导系数并在基质吸力较低时仍保持较大值[11]， 所以采用该种土工织物能实现路面结构在非饱和状态下的侧向排水. 其较小的孔隙还能避免周围土体颗粒进入防渗层中造成S型排水板淤堵. S型排水板是防渗层的组成结构， 根据其土水特性曲线上进水值只有几毫米的特点， S型排水板可阻隔水力传导层中的水分向下渗透.

通过市场调研发现， 非织造土工织物和S型排水板都能在工厂进行机械化大批量生产， 其经济效益和环境保护效益均大于传统碎石排水层， 且具备施工方便、 用途广泛和建成的道路路面质量较高等优点.

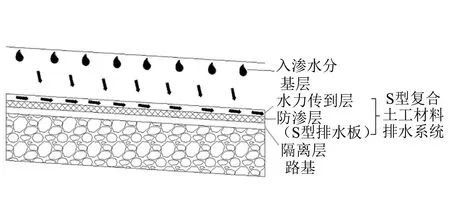
图1 S型复合土工材料排水系统断面

图2 S型复合土工材料排水系统组成形式

2 室内试验

2.1 试验目的

为验证所提出的S型复合土工材料排水系统在非饱和条件下排水的有效性， 在自制模型箱中构建小型路面结构并采用人工降雨系统模拟自然降雨， 通过安装在基层和路基中的监测传感器显示的数据变化来体现排水系统的效能.

2.2 试验装置

试验模型尺寸为180 cm×20 cm×58 cm， 如图3所示. 从上到下分别为基层、 S型复合土工材料排水系统和路基[12-14]. 基层厚度为150 mm， 由水、 水泥、 沙子和碎石组成. 路基土壤采用砂质粘土厚度为400 mm， 最大干密度为1.60 g·cm-3， 最优含水量为14.0%.

基质吸力由位于不同位置的张力计持续监测， 试验结束时， 根据实测基质吸力值和土水特性曲线计算土壤的体积含水量. S型复合土工材料排水系统的排水体积由非织造土工织物通过塑料集水管排至量筒中， 基层的排水体积由表面开有孔的集水管收集[12-14]， 如图4所示.

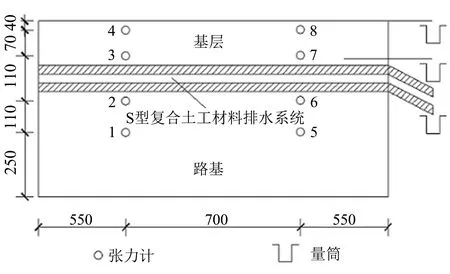
图3 室内试验设计图(单位： mm)

图4 排水量收集

2.3 试验步骤

图5 人工降雨系统

首先， 利用人工降雨系统模拟降雨90 min， 人工降雨系统由降雨管、 供水管、 压力表、 控制阀连接组成， 如图5所示. 在试验过程中， 通过控制供水管内的水压来调节降雨强度. 降雨之后， 测试水槽的顶部被一层塑料薄膜覆盖， 以减少水的蒸发. 试验数据共记录500 min (包括降雨90 min和雨停后410 min)， 基质吸力由预先安装在模型内部的张力计测量， 各结构层的排水体积通过预先设计的排水路线进入量筒中进行收集测量.

2.4 试验结果

基层变化结果如图6所示， 由于试验过程中发现监测点8处传感器失灵， 因此只记录了测点3、 4、 7的变化. 在整个试验过程中， 室内模型的基层始终处于非饱和状态. 基质吸力在第100 min时降到最低， 为18 kPa. 基层的体积含水率在模拟降雨过程中逐渐上升但未到达饱和含水率值. 图6中：Ψ为基质吸力值；θ为体积含水率， 下同.

图7所示为路基监测结果， 从图7中可看出， 新型排水系统还起到了防止水渗入路基的作用， 并且在试验过程中路基保持干燥. 不同的是， 其中有两个测点的吸力值减小了， 而另外两个测点的吸力值保持不变. 这种现象可能是由于模型箱体两侧缝隙中有少量水分进入路基引起的.

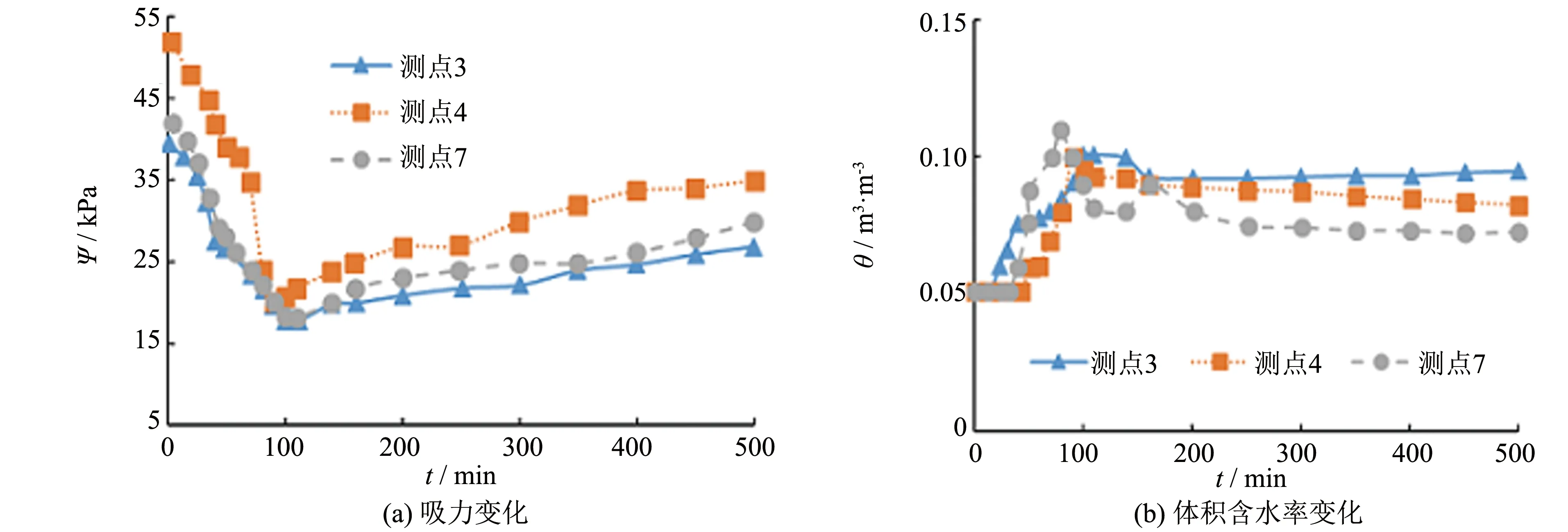
图6 室内试验基层变化

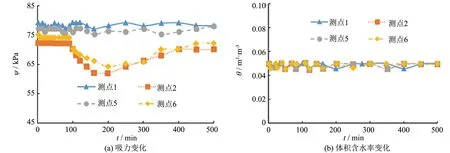
图7 室内试验路基变化

3 数值分析模型构建与验证

3.1 数值模型

数值模型使用了Geostudio(2007版)中的Seep/W模块， 数值模型中路面结构形式、 尺寸、 材料与室内试验保持一致， 如图8所示.

图8 数值模型

将模型表面的降雨强度设置为25 mm·h-1， 持续90 min. 模型的底部和左侧为零流量边界， 右侧为自由排水边界. 数值模型所使用的材料为Van Genuchte方程[15]预测的土水特性曲线和渗透性函数， 见下式， 具体参数取值如表1所示， 土水特性曲线和渗透性函数曲线如图9所示.

(1)

式中：θ，θr，θs为体积含水率、 残余体积含水率和饱和体积含水率；ks为饱和渗透系数；Ψ为基质吸力；a，n，m为曲线拟合参数， 其中n=1/(1-m).

表1 材料参数

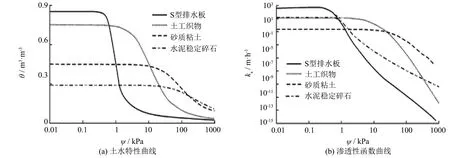
图9 材料的非饱和渗透特性

3.2 模型验证结果

数值模型计算结果与室内试验结果基本一致. 图10为基层数值计算结果与室内试验结果的对比图. 其中实测值大于数值计算结果， 原因可能是在试验过程中， 张力计中的气体没有完全排出， 使得测量的吸力值较大.

图10 新型路面排水系统基层变化

图11所示为路基数值计算结果与室内试验结果进行对比， 基质吸力初始值存在差异的原因是数值软件中计算初始基质吸力按照水压力沿地下水位向上延伸计算的[16]， 室内模型不受地下水位的影响. 从图11中可知数值分析与室内试验保持一致， S型复合土工材料排水系统发挥了防止水分向下渗透的作用， 路基始终保持初始状态.

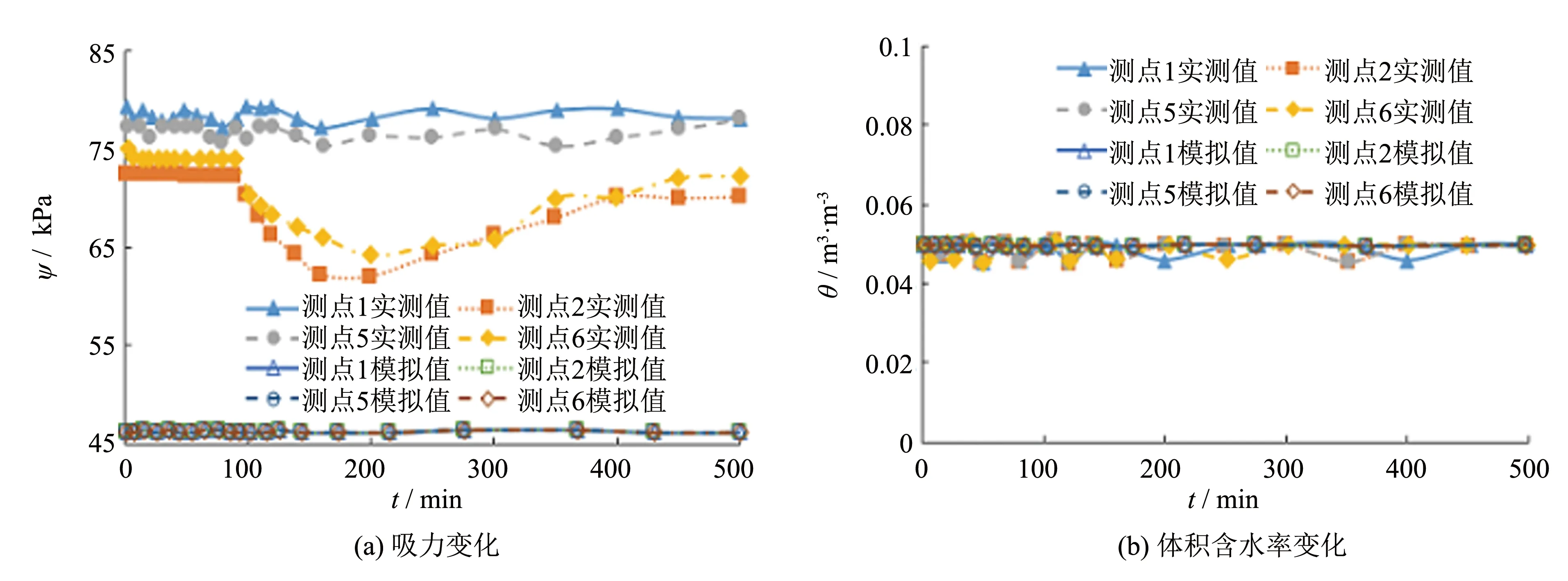
图11 新型路面排水系统路基变化

4 参数分析

通过以上论述， 数值模型很好地拟合了室内试验的结果， 并且S型复合土工材料排水系统能实现路基非饱和状态下排水的功能. 但从式(1)中可知， 土工织物的Van Genuchte模型中不同的参数取值会对材料渗透性产生影响[17-19]. 为研究S型复合土工材料排水系统中水力传导层土工织物的参数影响， 分别分析Van Genuchte 参数a值、 土工织物饱和渗透率ks、 土工织物厚度kt取不同值时对毛细屏障和突破时间产生的影响， 各参数取值范围详见表2. 表中ksg为土工织物饱和渗透率；ksc为水泥稳定碎石饱和渗透率.

表2 分析参数取值范围

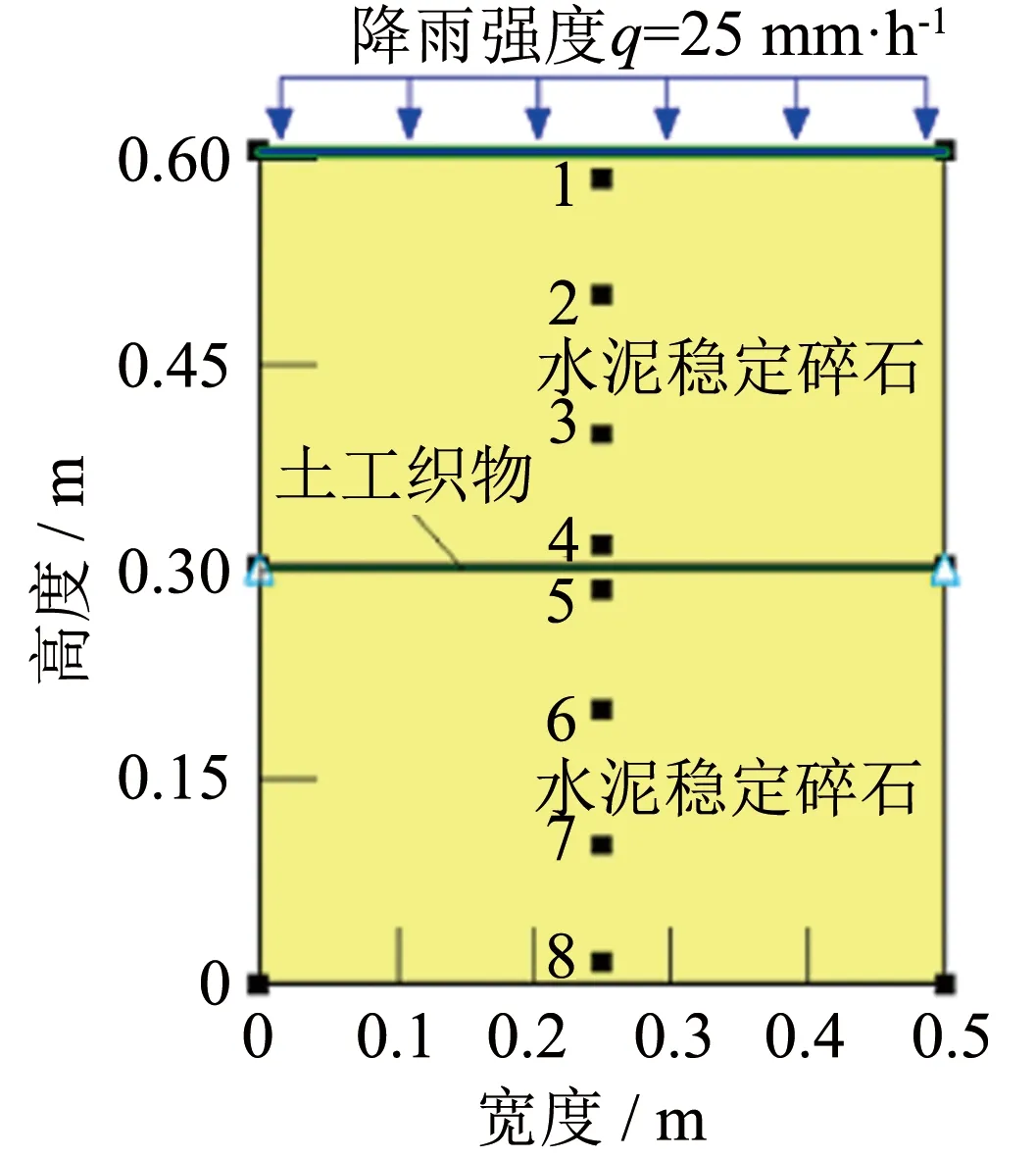
图12 参数分析模型设计图

参数分析模型如图12所示， 模型宽0.5 m， 土工织物上下各有0.3 m的水泥稳定碎石， 模型的顶部模拟室内试验的降雨条件， 土工织物和水泥稳定碎石的起始参数与室内试验相同， 见表1， 在土工织物上方和下方间隔0.1 m布置体积含水率和基质吸力监测点， 共计8个测点.

4.1 土工织物产生的毛细屏障作用

两种不同渗透性的材料接触时， 不可避免会在接触面形成毛细屏障[20]. 图13所示为在模拟降雨入渗过程中“突破”发生时， 有无土工织物水力传导层的两个模型的孔隙水压力对比图. 图13(a)中由于土工织物发挥了毛细屏障的作用， 入渗水聚集于土工织物层产生水平向排水， 而下层碎石材料始终处于高基质吸力状态. 图13(b)为同一时间但不含土工织物层的模型， 因为没有了毛细屏障作用导致水分一直向下渗透， 整个断面的孔隙水压力呈阶梯上升， 并且由于水分在模型底部积聚使得底部材料的基质吸力降低更快.

当“突破”发生时土工织物上方碎石材料达到的基质吸力越高或突破时间到来越早时， 意味着土工织物解除毛细屏障不利影响的能力越强. 因此可采用“突破”时的基质吸力和突破时间来评价不同参数取值对土工织物排水性能的影响[21-23].

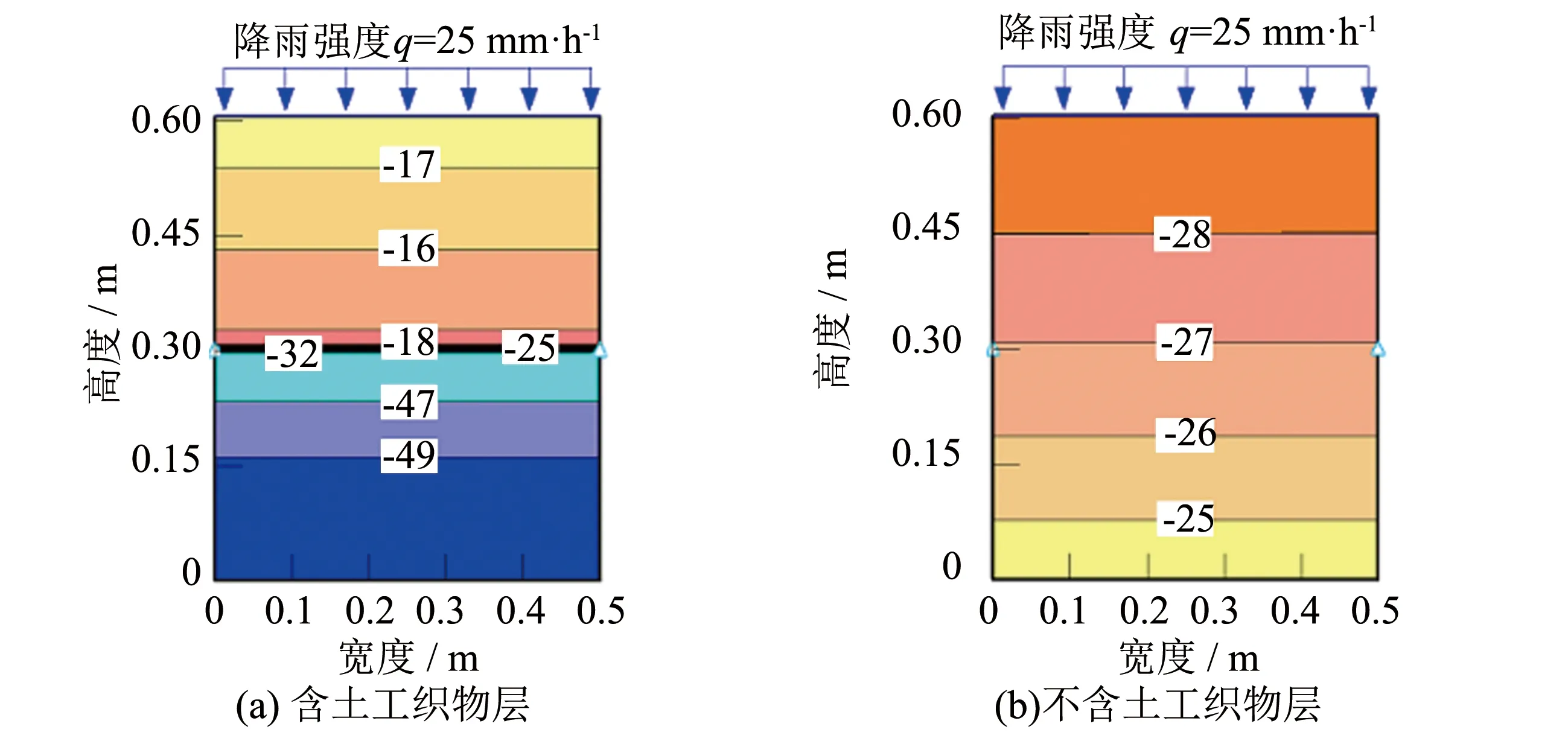
图13 孔隙水压力分布图

4.2 Van Genuchte参数a值

Van Genuchte模型参数a值， 其影响的是土水特性曲线中的进气值，a值增大则曲线向右移动. 根据“突破理论”，a值增大则土工织物与土层在土水特性曲线中的交点也会增大， 即土工织物可在较大的基质吸力条件下将土层中的水排出[24]. 研究a不同取值时对毛细屏蔽作用的影响， 土工织物其他参数为ks=0.003 5 m·s-1，kt=5 mm， 对应不同a值突破时各测点测得的基质吸力、 体积含水率、 突破时间如图14所示.

从图14中可知随着a值的增大， 土工织物上方各测点测得的基质吸力值逐渐增大、 体积含水率逐渐减小， 土工织物下方各测点的数据保持不变， 突破时间逐渐减小. 说明a值的增大有效减小了土工织物上方产生的毛细屏障的效果. 但是a值不能无限制增大， 在数值模拟中发现, 当a值取值大于10 kPa以后突破时间急剧缩短， 意味着水流将直接穿过土工织物进入路基层， 则无法实现前述室内试验验证的新型排水系统能防止雨水入渗到路基基层的效果. 根据数值模拟的结果建议a值取值在10 kPa左右.

图14 a值对毛细屏障的影响

4.3 土工织物饱和渗透率ks

土工织物作为水力传导层， 饱和渗透率是一个很重要的参数， 饱和渗透率越大意味着土工织物的排水能力越强. 为了研究饱和渗透率的影响， 设置土工织物的饱和渗透率从水泥稳定碎石的饱和渗透率开始增大， 数值模拟结果如图15所示. 在该研究中土工织物的其他参数取值为a=10 kPa，kt=5 mm.

饱和渗透率体现了土工织物的排水性能， 从图15可知， 随着土工织物饱和渗透率的逐渐增大， 突破时土工织物上方各测点测得的基质吸力值逐渐增大， 体积含水率逐渐减下， 意味着土工织物饱和渗透率的增大也能有效减小毛细屏障的效果. 由实际工艺可知, 饱和渗透系数不能无限制增大， 因此结合数值结果建议ks取值范围为0.01～0.10 m·s-1.

图15 土工织物饱和渗透率对毛细屏障的影响

4.4 土工织物厚度kt

取土工织物不同厚度值进行数值模拟来研究其对降低毛细屏障的影响， 该研究中土工织物的其他参数取值为ks=0.003 5 m·s-1，a=10 kPa.

数值模拟结果如图16所示， 从图16中可看出， 随着土工织物厚度的改变， 突破时土工织物上方各测点测得的基质吸力、 体积含水率以及突破时间的变化都不大， 可知土工织物厚度对毛细屏障作用的影响并不显著. 在目前公路建设中以采用级配碎石作为道路路基的排水层为主， 厚度大且对碎石材料要求高. 采用S型复合土工材料排水系统可以降低道路铺筑厚度、 节省施工成本， 并且铺筑S型复合土工材料排水系统比铺筑级配碎石所需工期更短[25].

图16 土工织物厚度对毛细屏障的影响

5 结语

1) 室内模型试验结果表明， 在模拟降雨停止后10 min， 基层基质吸力开始回升并且在全过程基层的基质吸力都没有降低到零值； 全过程路基层的基质吸力和体积含水率始终保持在初始值. 室内模型实验结果表明S型复合土工合成材料排水系统能实现路面结构在非饱和条件下排水， 并保护路基免受水分侵害.

2) 数值模拟结果与室内模型试验基本保持一致， 验证了数值模型建模和参数选取的正确性.

3) Van Genuchte参数a和土工织物饱和渗透系数ks是影响水力传导层排水性能的主要参数， 随着a值和ks的增大， 在非饱和条件下的排水效果越好. 结合分析结果和工程应用实际， 建议a值取10 kPa左右，ks取值范围为0.01～0.10 m·s-1. 而分析中发现土工织物厚度对减小毛细屏障作用的效果并不显著， 给出厚度的参考取值范围为10～15 mm.

4) 在本文研究的基础上， 下一步需结合实际工程应用情况研究S型复合土工合成材料排水系统的淤堵和耐久性等问题， 评估S型复合土工合成材料排水系统的长期有效性.