自复位耗能摇摆架加固软弱底层框架抗震性能

2021-04-23姜绍飞戴亮亮张漳荣

福州大学学报（自然科学版） 2021年2期

姜绍飞，戴亮亮，张漳荣

(福州大学土木工程学院, 福建福州 350108)

0 引言

软弱底层框架因其底层大空间而被广泛应用商业活动中，如停车场、商场、大厅等. 由于底层很少布置或不布置墙体，造成竖向刚度差异较大，形成“上刚下柔”的结构形式，地震时软弱底层吸收了大部分地震能量，造成结构底层侧向变形集中和损伤集中，往往底层完全倒塌了，上部结构却完好无损[1-2]. 再加上楼板对框架梁和柱顶约束作用的影响，很难实现“强柱弱梁”的设计目标[3].

已有的研究表明[4-8]，底部铰接的摇摆结构在控制框架结构侧向变形模式方面效果显著，摇摆结构利用自身的抗弯刚度和强度对框架受到的内力进行重新分配，从而使结构层间变形均匀，避免发生软弱层破坏，而且配合自复位装置和耗能装置可以进一步提升结构的自复位能力和耗能能力.

因此，提出一种底部铰接的自复位耗能(SCED)摇摆架加固方案，并介绍了SCED摇摆架的构造及布置形式. 对SCED摇摆架-软弱底层框架进行受力性能分析，初步推导出预应力钢绞线和装配式屈曲支撑(BRB)的设计计算方法；并建立有限元模型对比研究未加固、 SCED摇摆架加固、 ED摇摆架加固和纯摇摆架加固的抗震性能，为软弱底层框架的摇摆架加固设计提供一种参考.

1 SCED摇摆架的构造及布置形式

SCED摇摆架的构造示意图如图1所示. 摇摆架底部利用工字型钢凹槽，两侧各布置2个由防屈曲耗能芯材、填充板和外约束盖板装配而成一种装配式BRB，一旦发现损坏，可以快速方便地更换，立即恢复其功能，详细构造如图2所示. 当BRB受到轴力作用时，由核心板承受全部的轴力，外约束盖板和填充板约束芯材的弯曲，避免芯材受压屈曲. 摇摆架的自复位能力由两端张拉的预应力钢绞线来提供，钢绞线顶端与摇摆架顶端通过锚固连接，底端与基础相连.

图2 装配式BRB构造示意图(单位： mm)

SCED摇摆架加固软弱底层框架的布置形式如图3(a)、 (b)所示. 摇摆架通过抗剪连接件与软弱底层框架梁相连，参考曹海韵等[9]对摇摆墙抗剪连接件的设计，提出SCED摇摆架-软弱底层框架的连接构造如图3(c)所示. 该抗剪连接件可以上下滑动，以实现摇摆架与软弱底层框架梁之间在竖向的变形协调.

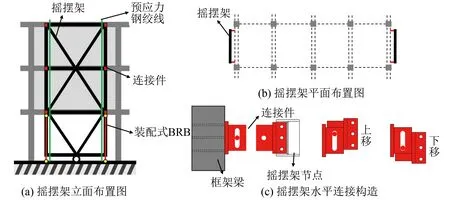
图3 SCED摇摆架的布置形式和连接

2 SCED摇摆架-软弱底层框架受力性能分析

图4 SCED摇摆架-软弱底层框架的受力分析模型

在水平力作用下SCED摇摆架-软弱底层框架的受力情况如图4所示. 从图4中可以看出，钢筋框架与摇摆架之间的水平剪力转化成刚性连杆中的轴力，底层V型支撑之间为理想的铰. 钢筋摇摆架通过自身的刚度限制结构沿竖向发生不均匀变形. 考虑控制结构的变形机制，摇摆时通过两边的装配式BRB耗能，并由预应力钢绞线提供自复位能力.

软弱底层框架结构在水平侧向力作用下的倾覆力矩由下式计算：

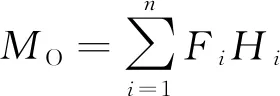
(1)

式中：MO为软弱底层框架的倾覆力矩；Fi为按《建筑抗震设计规范》[10]计算的等效侧向力；Hi为第i层高度.

SCED摇摆架承担的抗倾覆力矩由框架结构的倾覆力矩乘以一个系数λ决定. 《高规》[11]规定，当框架部分承受倾覆力矩大于结构总倾覆力矩的80%时，框架-剪力墙结构中的框架部分应按框架结构的规定进行设计. 同样，对于SCED摇摆架不会改变现有框架的设计要求，当λ在0.15～0.20范围内时，框架所承受的倾覆力矩抗力的比例在83.3%～87.0%， Wu等[12]建议λ取0.16. 当选定λ的值时，摇摆架承受的倾覆力矩计算如下：

Mr≥λMO

(2)

式中：Mr为SCED摇摆架的抗倾覆力矩；λ为SCED摇摆架的抗倾覆力矩与软弱底层框架的倾覆力矩之比.

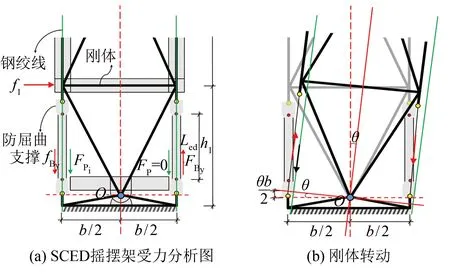
图5 SCED摇摆结构分析模型

SCED摇摆架底部的受力分析模型如图5所示. 为设计预应力钢绞线和装配式BRB，假定粗线部分为刚体，忽视摇摆架的重力. 两个红点间的距离Led为BRB的核心耗能段长度，核心段长度对支撑的屈曲耗能影响很大，取值范围建议在0.3～0.7倍的支撑长度[13]. 绿线代表预应力钢绞线，要求始终保持弹性状态. 其抗倾覆力矩Mr由钢绞线的自复位力矩MPT和BRB屈服力矩MBRB决定，将式(2)展开可得：

MPT+MBRB≥λMO

(3a)

FPi=φfptkAPT,FBy=0.9fyABRB

(3c)

式中：b为摇摆架宽度；FPi为钢绞线初始预拉力值；FBy为BRB的屈服力；φ为钢绞线初始预应力百分比；fptk为钢绞线极限强度标准值；APT为钢绞线的截面积；ABRB为BRB核心段的截面积；fy为核心段的屈服强度.

当所受水平荷载结束时，结构体无外力作用，由钢绞线提供自复位力矩，克服BRB的塑性变形. 定义一个自复位系数β，为自复位力矩MPT和BRB屈服力矩MBRB之比，可根据设计需求取β≥1的值：

β=MPT·MBRB-1

(4)

由式(3)和(4)即可初步计算设计所需的预应力钢绞线和BRB的设计参数.

3 有限元模型及验证

3.1 分析模型

选取文献[14]中的P0试件作为SCED摇摆架加固分析的对象，加固后的示意图如图6(a)所示， SCED摇摆架的构造示意图如图1所示，装配式BRB的构造示意图如图2所示.

摇摆架的跨度b=900 mm，梁、柱为125 mm × 125 mm × 6.5 mm × 9 mm的H型钢，斜撑100 mm ×100 mm × 6 mm × 8 mm的H型钢，钢材等级为Q345. BRB核心板采用LY160级软钢，耗能段和盖板或填板的间隙为1 mm，并填充间隔材料. 预应力钢绞线按照《混凝土结构设计规范》[15]采用7股钢绞线，公称直径为17.8 mm，面积为191 mm2，极限强度标准值fptk=1.862 GPa，弹性模量取195 GPa，初始张拉预应力值为钢绞线屈服应力的30%，该试件记为RF-1. 另外设置两组对照组RF-2和RF-3，如图6(b)、 (c)所示. RF-2为不设置钢绞线和BRB的纯摇摆架加固模型. RF-3为设置BRB、不设置钢绞线的ED摇摆架加固模型.

3.2 建模方法及加载制度

ABAQUS有限元建模如图7所示. 混凝土单元类型为C3D8R，本构采用ABAQUS自带的混凝土损伤塑性模型. 钢筋单元类型为T3D2，通过Embed命令嵌入混凝土中. 由于ABAQUS自带的钢筋滞回规则并没有考虑钢筋滑移，采用方自虎等[16]开发的钢筋模型(见图8)子程序来模拟钢筋的滑移效果. 模型基础梁底面固接，确保加载过程中基础不发生移动，梁柱节点处约束侧向的移动，防止加载过程中面外失稳.

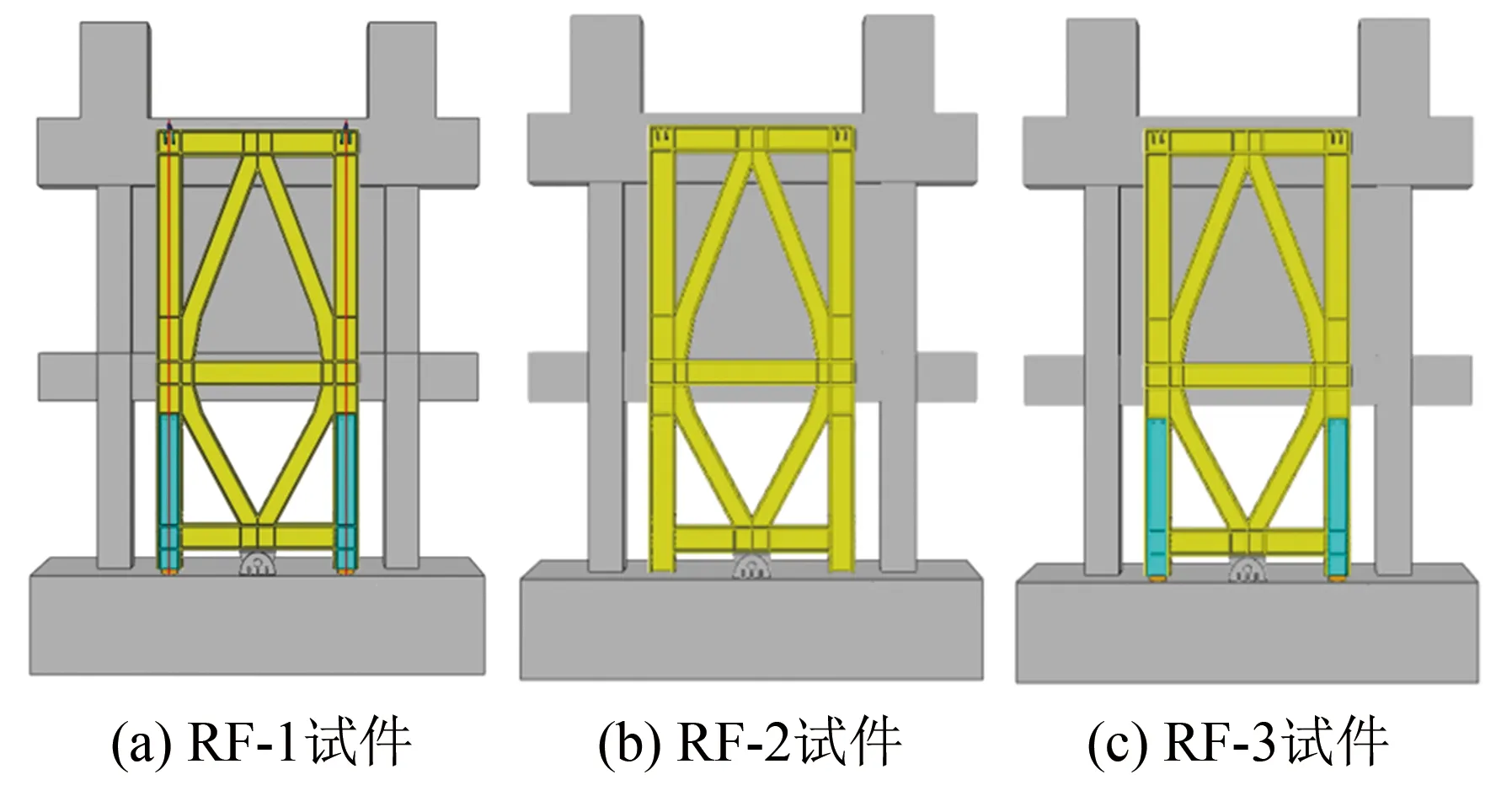
图6 三组加固试件

图7 有限元模型

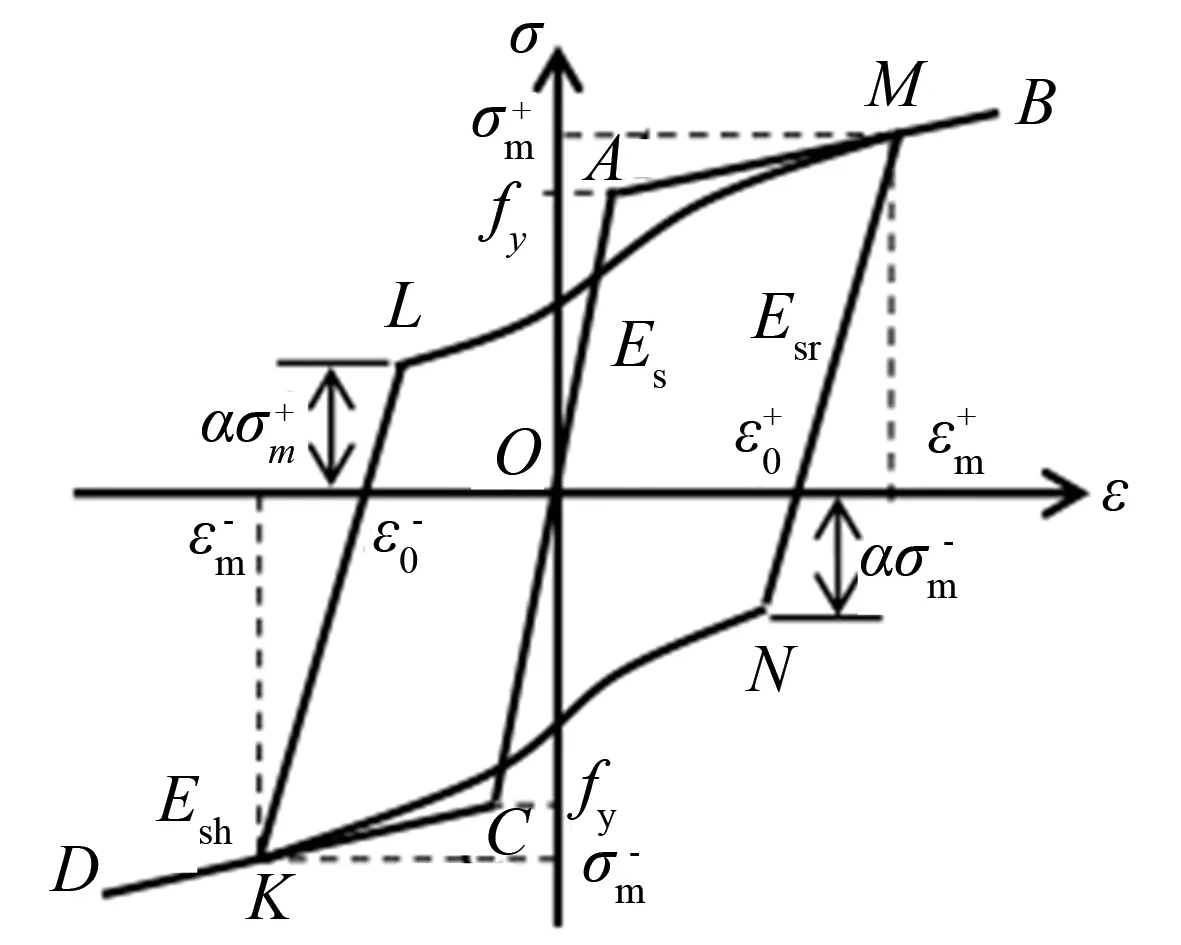
图8 方自虎钢筋模型

摇摆架采用壳单元S4R模拟，钢材本构为二折线随动硬化模型. 对摇摆架底部铰接基础进行简化，在摇摆架底部、基础梁顶面设置一个参考点，并用MPC-beam连接到摇摆架底部，释放该参考点绕加载方向的转动. 摇摆架与框架之间的水平连接采用梁单元B31来模拟，梁单元的一端与摇摆架节点通过MPC-beam约束连接，另一侧与软弱底层框架梁预埋件通过耦合相连，并放松该侧Z方向的滑动和绕Y轴方向的转动，只传递楼层的水平剪力. 连接的可靠性是保证框架与摇摆架协同工作的关键，因此将水平连接单元的刚度设置成一个大数.

为保证计算的效率和收敛性，装配式BRB采用桁架单元T3D2来模拟. BRB的滞回曲线饱满，在设计合理的情况下，其拉压基本对称，而桁架单元只受轴力作用，且具有拉压对称性，可以应用于BRB建模.

钢绞线采用桁架单元T3D2来模拟，利用等效降温法来模拟施加在钢绞线上的预应力，膨胀系数α=1.02×10-5. 模拟时仅考虑钢绞线的拉力，钢绞线与垫板通过MPC-beam连接，垫板与摇摆架顶部绑定，钢绞线通过垫板作用在摇摆架上.

加载制度与文献[14]保持一致，第一步先在框架两个柱头施加竖向荷载，轴压比为0.2；第二步施加水平荷载，在ABAQUS中建立位移约束方程(Equation)，保持一层和二层的出力比为5∶6. 水平循环加载以首层的层间位移角控制，分别为±0.125%、 ±0.25%、 ±0.5%、 ±0.75%、 ±1.0%、 ±1.5%、 ±2.0%、 ±2.5%、 ±3.0%、 ±4.0%和±5.0%，每级各循环一次.

3.3 模型验证

1) 混凝土框架. 将文献[14]的软弱底层框架试验结果与有限元模拟结果对比，滞回曲线如图9(a)所示. 由图可知，试验和模拟的滞回曲线基本重合，只是在反向的承载能力上有点差异. 这说明对混凝土框架的建模方法得到了保证.

2) BRB等效建模. 为验证桁架单元等效建模BRB的准确性，采用文献[17]中SUB-1试件的精细化建模结果与本研究的等效简化建模结果进行对比. 材料本构选用双线性随动硬化本构，将SUB-1核心段的截面积等效为桁架单元的截面积，对比结果如图9(b)所示. 可以看到，等效简化的滞回曲线和精细建模的滞回曲线基本吻合，说明桁架单元建模BRB也是有效的.

3) 复位机制. 为尽力还原预应力钢绞线在结构体系中的自复位机制，将有限元仿真与文献[18]中的体外预应力自复位框架受控体系EPSCF的试验进行验证. 钢绞线采用3.2节建模方法，数值模拟的结果与试验结果的对比如图9(c)所示. 可以看出，数值模拟的结果与试验结果吻合较好.

4) BRB-摇摆架. 钢筋摇摆架和BRB均采用3.2节提出的建模方法，所选择的各参数均与文献[19] 带BRB柱的摇摆钢架GK2保持一致. 二者对比的结果如图9(d)所示. 从图中可以看出，本研究模拟结果吻合较好，保证了建模的可靠性.

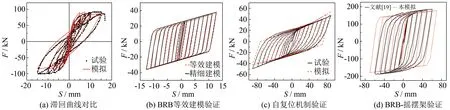
图9 有限元模型验证

4 抗震性能分析

4.1 破坏过程及现象

钢筋摇摆架加固前后的结构破坏模式如图10所示. 其中，未加固的框架钢筋应力云图如图10(a)所示，摇摆架加固的钢筋应力云图如图10(b)～(e)所示. 通过对比发现， RF-1、 RF-2和RF-3三个试件的混凝土框架破坏模式基本相同. 加固前钢筋应力主要集中在软弱底层，二层剪力墙未见应力分布，是典型的软弱底层破坏模式；加固后随着位移角的增大，二层剪力墙开始发挥作用，钢筋开始屈服耗能并提供抗侧刚度，破坏模式得到改善. 以RF-1为例分析软弱底层框架的破坏过程，当位移角达到0.5%时，底层柱子的纵筋达到屈服应力355 MPa；加载到1%时，底层柱底箍筋开始屈服，屈服应力为683 MPa，此时剪力墙底部开始出现较大的应力分布；加载到2%时，剪力墙底部竖向钢筋达到屈服应力683 MPa，说明此时剪力墙开始屈服；加载至极限层间位移角5%时，此时剪力墙钢筋有大量的应力分布. 说明剪力墙钢筋屈服，出现塑性铰区，能量主要由剪力墙塑性铰区的钢筋屈服来耗能.

图10 摇摆架加固前后结构的破坏模式

RF-1、 RF-2和RF-3三个试件的摇摆架极限状态下的应力云图如图11所示.

图11 摇摆架应力分布云图

三种摇摆架的破坏模式明显不同： RF-1摇摆架的底层支撑进入塑性状态，破坏程度最严重，其次是RF-3和RF-2. 由此可以发现, 增加钢绞线和BRB会对摇摆架的整体破坏产生不利的影响，这是由钢绞线和BRB传递到摇摆架底层支撑的作用力以及摇摆架底层承受的剪力共同作用的结果；而摇摆架的破坏最终会影响到对结构体系层间变形的控制. RF-2的摇摆架破坏点主要集中在梁端的部分翼缘，对摇摆架整体的破坏影响不大.

4.2 滞回曲线

各试件的滞回曲线如图12所示. 其中，未加固的软弱层框架的滞回曲线如图12(a)， SCED摇摆架、纯摇摆架和ED摇摆架加固后的滞回曲线分别如图12(b)～(d)所示. 图中，横坐标为首层位移，纵坐标为基底剪力，即两个加载点的水平力之和. 可见，相对于未加固框架，三种摇摆架分别加固后，滞回曲线更加饱满，变形能力、刚度和承载能力均有明显提升. 相比于RF-2和RF-3试件， RF-1试件的滞回曲线捏缩现象明显，荷载卸载至零时的曲线在位移轴上的截距更小，这得益于预应力钢绞线的加入，提高了结构的自复位能力，减小结构的残余变形. 试件RF-3比RF-2试件的滞回曲线更加饱满，这是因为RF-3增设了耗能装置，提升了结构的耗能能力.

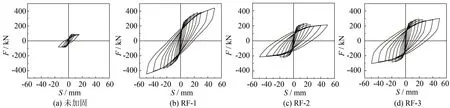
图12 各试件滞回曲线

4.3 骨架曲线

图13 骨架曲线

骨架曲线如图13所示. 由图13可见， RF-1、 RF-2和RF-3试件在0.5%层间位移角时，骨架曲线开始出现比较明显的斜率下降，此时对应框架底层柱底的纵筋屈服，说明此时结构开始进入塑性阶段；当加载至2%层间位移角时，骨架曲线有下降的趋势，这是因为此时剪力墙的钢筋开始屈服，但是随着荷载增大，仍然具有承载能力. 在弹性阶段， RF-1和RF-3的曲线基本重合，且高于RF-2试件，说明两者刚度比较接近且大于RF-2；在塑性阶段后期， RF-1的骨架曲线呈现了比较明显上升，这是因为钢绞线发挥比较大的作用，提升了结构的承载能力. 相比于未加固试件， RF-1的极限承载能力是未加固试件的442%， RF-2和RF-3分别是未加固试件的211%和301%.

4.4 变形模式

摇摆架的刚度对软弱底层结构的侧向变形模式的控制具有很大的影响，一般采用层间位移集中系数DCF表示,

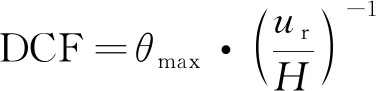
(5)

式中：θmax为所有楼层层间位移角的最大值；ur为结构顶点位移；H为结构总高度. DCF越大，说明侧向变形越集中； DCF趋近于1，说明结构侧向变形越均匀.

图14 层间位移集中系数

三种摇摆架加固和未加固的构件达到极限位移时的DCF如图14所示. 未加固时结构的DCF为1.93，加固后结构DCF最小为1.2，最大的为1.28，说明加固后侧向变形更加均匀，对结构变形模式控制更强. 但是RF-1和RF-3的DCF明显大于RF-2，说明钢绞线和BRB的存在降低了摇摆架对框架层间变形的控制能力. 通过前述的受力分析知道，在侧向受力不变的情况下，增加钢绞线和BRB能够为其提供抗倾覆力矩，增加其抗侧刚度，同时会一定程度降低摇摆架的层间反作用力(如图12的滞回曲线所示). 因此，虽然SCED摇摆架对结构变形控制效果不如纯摇摆架，但其可以有效降低结构的侧向位移，而纯摇摆架能够较好控制层间变形，但对结构侧向位移的控制不如SCED摇摆架，以上结论与文献[20]所得的结论相一致，也验证了本研究的受力分析与仿真模拟的准确性. 综上所述，建议层间变形为控制目标的结构采用纯摇摆架加固，侧向变形为控制目标的结构采用SCED摇摆架加固.

4.5 自复位能力

荷载卸至零时的变形为残余变形，用相对残余变形来评价各试件的自复位能力大小，定义为:

(6)

其中：Rrd为相对残余变形；Δri+、Δri-每级正反向卸载后的残余变形；iΔ+、Δi-为每级正反向最大位移.

各试件的相对残余变形随层间位移角曲线如图15所示. RF-1和RF-3在达到屈服前的相对残余变形相差不大；屈服后RF-3残余变形继续上升并逐渐累积；而RF-1试件的曲线先上升后下降，这是因为前期预应力钢绞线尚未发挥较大的作用，随着预应力逐渐增大，残余变形开始减小；而RF-2加固由于没有预应力的存在，残余变形也是逐渐累积，曲线一直呈现上升的趋势，但由于没有耗能装置，其相对残余变形比RF-3小. 当达到5%位移角时， RF-3相对残余变形接近60%， RF-2为51%， RF-1最小为36%. 表明SCED摇摆架加固后的RF-1试件残余变形最小，自复位性能最好.

4.6 耗能能力

各试件的累积耗能对比如图16所示. 从图中可见，所有试件累计耗能均随层间位移角逐渐增加，其中RF-1和RF-3增长更明显，且RF-3的累积耗能稍高于RF-1，说明预应力钢绞线会削弱结构耗能. 由第2节的受力性能分析可知，当摇摆架复位时，由预应力钢绞线提供自复位力矩会和BRB产生的力矩相互抵消，降低结构的耗能能力. 当达到极限位移时， RF-1和RF-3的累积耗能均为RF-2的1.6倍以上.