基于Kramers-Kronig关系的油纸绝缘直流电导计算方法

何津, 邹阳

(福州大学电气工程与自动化学院, 福建 福州 350108)

0 引言

油纸绝缘作为一种经典的复合绝缘介质， 具有绝缘性能良好、 成本低廉、 取材方便等优点， 广泛应用于电力系统的变压器、 绝缘套管等设备上[1]. 油纸绝缘在运行过程中受到电、 热、 机械力的作用， 难免发生老化劣化的现象， 若不及时处理， 将导致设备故障， 造成不必要的损失. 目前针对油纸绝缘状态的检测方法分为传统诊断方法和介电响应诊断法， 而后者具有携带信息量大， 抗干扰强、 无需吊芯等优点， 更适合于现场诊断， 成为研究热点[2].

介电响应诊断法有时频域之分， 其中时域响应有回复电压法、 极化-去极化电流法， 频域响应有频域介电谱法. 无论是时域还是频域， 油纸绝缘的介电响应谱线都包含丰富的绝缘状态信息. 文献[3]分析了不同绝缘状态下回复电压最大值、 主时间常数和初始斜率等回复电压极化特征量的变化规律； 文献[4]用极化-去极化电流法测量了不同服役时间变压器的水分质量分数， 详细地分析了变压器老化过程与水分质量分数的关系； 文献[5]发现随着绝缘油电导率增加， 低频域电导损耗特性逐渐向高频扩展， 却无法将电导损耗谱线分离出来； 文献[6]基于扩展德拜等效电路， 验证了最小和最大时间常数支路中的RC参数能反映绝缘纸的老化状态， 但其模型参数的确定具有随机性； 文献[7]基于去极化电流谱， 提出微分解谱法确定扩展德拜模型的极化支路参数， 但无法确定模型中的绝缘电阻. 以上研究表明， 对于利用油纸绝缘介电响应来诊断老化状态取得一定的成果， 但是还存在对介电谱信息挖掘不够深刻， 等效模型中描述电导的参数无法唯一确定的问题.

针对以上问题， 本研究在油纸绝缘样品FDS测量数据的基础上， 提出基于Kramers-Kronig关系的油纸绝缘直流电导计算方法. 首先， 在实验室的条件下制备不同水分含量的油纸绝缘样品， 并利用Dirana介电分析仪测量其频域响应谱线； 然后， 根据Kramers-Kronig关系对测量复极化率实部谱线进行积分， 获得剔除电导后的弛豫损耗谱线， 进而得到电导损耗谱线； 最后， 使用最小二乘法对电导损耗谱线进行拟合， 结合电导在双对数坐标系的频域特性， 计算出电导值， 并验证其正确性.

1 频域介电响应特性分析

1.1 复电容的实部和虚部之间的关系

在交变电场中， 油纸绝缘介质同时存在带电粒子的转移过程和表面结合效应， 分别导致电导过程以及极化过程. 随着电场频率的变化， 极化和传导过程发生不同程度的响应， 材料中输出电流的相位和幅度也会发生变化. 复电容是关于电流和电压的函数， 可以反映电荷的传导和极化[8]， 公式如下：

(1)

其中：I(ω)和U(ω)是响应复电流和施加的复电压；C′(ω)和C″(ω)是复电容C(ω)的实部和虚部.

此外， 复电容、 复介电常数及复极化率之间的关系如下：

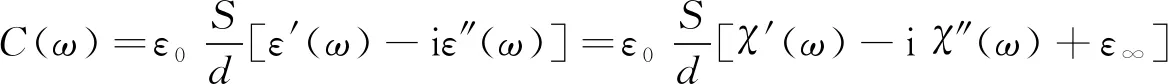
(2)

1.2 直流电导与低频色散区别

由FDS测量获得的实际介电谱是由极化和电导组成的综合响应， 而电导的频域特性为：

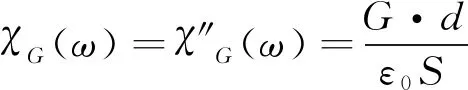
(3)

上式意味着电导G对于复极化率的实部的贡献为0， 所以由FDS测量得到复极化率实部不包含电导， 而复极化率虚部则包含电导损耗和极化损耗两个部分， 用以下式子表示：

(4)

由式(3)可以看出， 电导正比于ω-1， 即频率越低， 电导损耗越大， 这与文献[9]强调介电谱虚部低频段由电导损耗主导一致， 而对低频段的极化损耗以及其微观响应机制的探讨较为缺乏[10]， 因此油纸绝缘FDS测量曲线的具体物理机制仍存在争议[11].

文献[12]在对数百种介质的介电响应研究后发现， 在低频范围存在一种不同于电导的介电现象， 并称之为低频色散(low-frequency dispersion, LFD). 低频色散过程的特征是其复极化率的实部和虚部具有很强的分散性. 换而言之， 其复极化率的实部与虚部谱线会随着频率的增加而下降[12]， 其表达式如下：

χ(ω)=A(iω)n-1

(5)

式中：A是常数， 指数n小于1. 当n较小时， 意味着响应电流随时间的变化较为缓慢， 因此可以将其描述为“准直流电流”(quasi-d.c)[12]. 因此当低频范围内极化弛豫过程和直流电导过程耦合在一起时， 低频色散过程常常被直流电导分量掩盖， 无法对其进一步研究， 甚至也有直流电导过程被误作弛豫过程处理的情况发生[13]. 然而LFD与真正的直流电导之间的根本区别在于直流电导并不涉及系统中的任何电荷存储.

2 基于Kramers-Kronig关系的直流电导计算步骤

电介质的极化率实部和虚部是由同一个介质的响应函数分离出来的， 因此两者之间有不可切割的联系， 即Kramers-Kronig关系. 直流电导过程不产生电荷的存储， 对极化率实部的贡献为0， 因此， 通过Kramers-Kronig变换由实部获得的虚部谱线为剔除直流电导后的极化损耗谱线. 结合式(4)， 可以进一步计算获得直流电导损耗谱线.

2.1 Kramers-Kronig关系

在因果律成立的前提下， Kramers-Kronig关系可以表示为[14]：

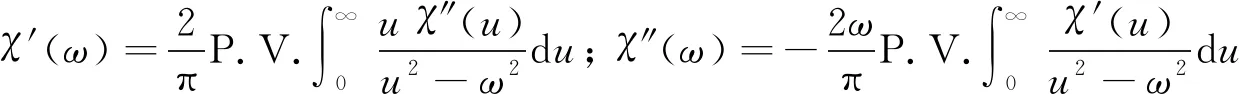
(6)

其中： P.V.表示柯西积分主值；u为奇异点频率.

从上式可以看出， 某一特定频率点的复极化率虚部是由整个连续频率范围内的复极化率实部积分而得到， 然而在实际的测量中， 受到设备的限制， 只能获得有限频率范围内的离散测量值. 另外， 在积分的过程中奇异点的存在导致需要用到柯西主值积分的定义， 二者都给计算带来了极大的困难.

2.2 直流电导计算步骤

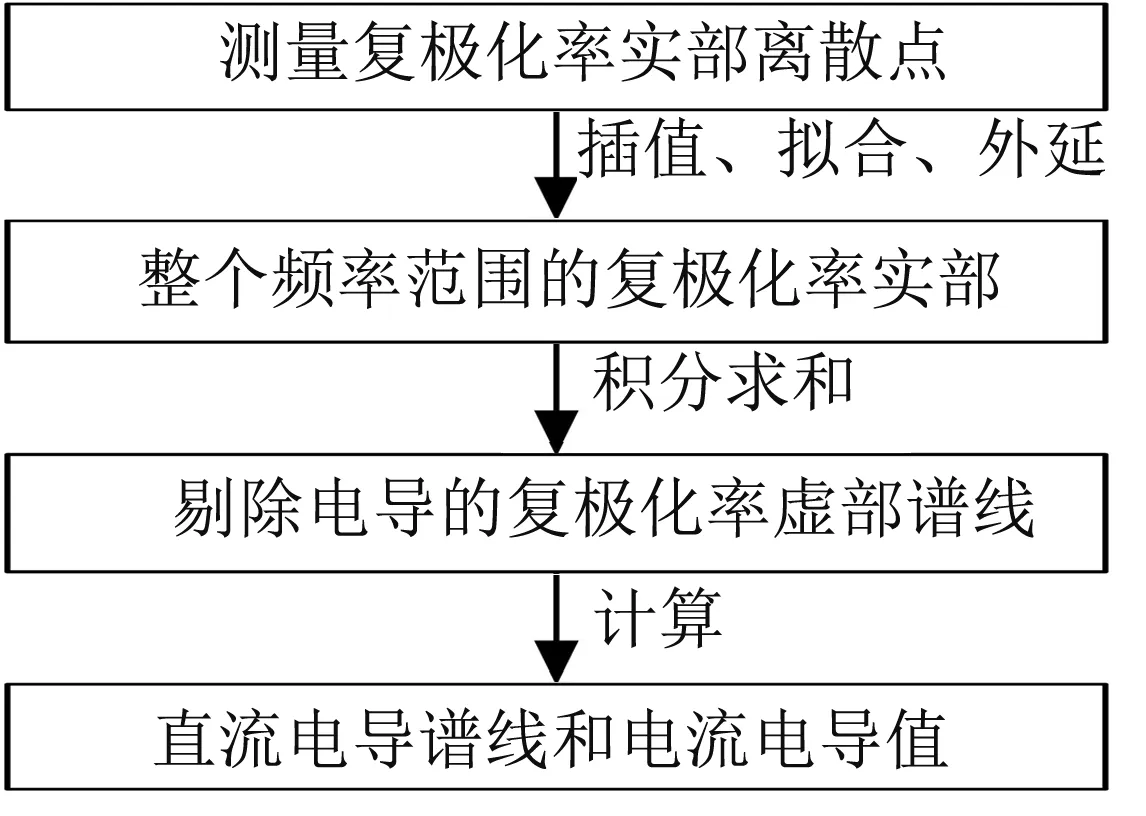
图1 直流电导计算步骤示意图

为解决以上问题， 本研究使用最小二乘法对复极化率测量离散点进行插值或拟合， 并在最低(高)频率测量点处外延一个数量级， 以保证频率测量点处计算得到的剔除电导的复极化率虚部尽可能准确； 另外， 对于奇异点积分， 本研究以奇异点频率fu附近的两个频率点作为积分上下限， 采用直线对此区间的近似曲线进行拟合， 最后通过牛顿-莱布尼茨公式进行积分计算.

计算步骤示意图如图1所示. 具体而言， 按照以下步骤来获得剔除电导的弛豫损耗谱线以及直流电导.

1) 以f1(fN)表示测量点的最低(高)频率， 用最小二乘直线对最低(最高)两个或者三个测量频率点进行插值或拟合， 如下式所示， 并以辛普森法则计算积分：

lnχ′(f)=Blnf+C

(7)

式中，B、C表示最小二乘直线系数.

2) 将直线外延一个数量级， 得到χ′(0.1f1)和χ′(10fn). 设χ′(f)在0.1f1和10fN之外的响应均为常数， 因此会有额外的贡献：

(8)

3) 根据普适弛豫定理， 介电响应数据在双对数坐标系下通常是非常平滑的， 因此使用抛物线对剩余测量点每三个点之间进行插值， 如下式， 并以辛普森法则进行积分计算.

lnχ′(f)=A(lnf)2+Blnf+C

(9)

式中：A、B、C表示插值抛物线系数.

4) 设奇异点频率fu附近的两个频率点分别为fu1和fu2， 采用最小二乘直线对区间(fu1,fu2)的曲线进行拟合， 并计算积分， 表达式如下所示：

(10)

式中：a、b表示拟合直线系数.

3 实验结果与分析

为验证电导计算方法的正确性， 本研究制作了三组不同含水率的油纸绝缘样品， 并对其进行FDS测量. 根据第2.2节所述步骤， 对频域介电响应数据进行分析， 最终计算得到样品的直流电导.

3.1 样品制备

采用厚度为 1 mm 的普通纤维绝缘纸板和25号环烷基矿物油制备用于测试的油浸纸样品. 首先， 将绝缘纸板裁剪为多块 100 mm×80 mm 大小合适的长方形， 绝缘油分为多组放入可密封玻璃容器中. 接着， 将绝缘纸和绝缘油分别放在105 ℃的恒温干燥箱中干燥24 h. 然后， 将干燥处理过的绝缘纸样品放置于高精度电子天平上， 进行自然吸潮直至满足目标实验质量. 最后， 将受潮的绝缘纸板浸入绝缘油中48 h， 确保绝缘油充分地浸润纸板空腔， 并将油纸绝缘样品密封在专用容器中， 以防止水分进入. 本次实验获取四组油纸绝缘试品的水分含量分别为： 0.244%、 1.58%、 2.77%和 3.63%.

3.2 油纸绝缘样品的测量数据分析

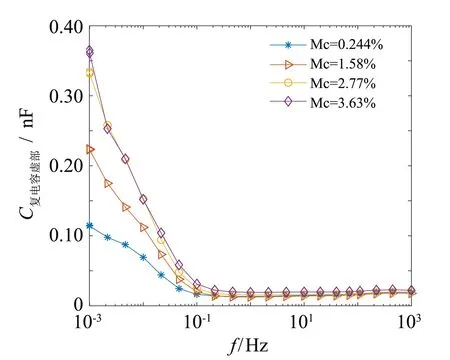
实验获得了频率范围在10-3～103Hz之间不同含水率的油纸绝缘样品复电容曲线， 如图2所示.

(a) 复电容实部曲线

图2中不同含水率样品的复电容实部均随着测量频率的升高而减小， 复电容虚部同样也是随着频率的升高而减小， 但是相较于实部谱线， 其数量级大了1级， 不同含水率样品谱线之间的差别更明显， 因此复电容虚部对于水分的敏感度更高. 随着绝缘纸水分含量的升高， 复电容实部和虚部均呈现增大的趋势， 在10-3～103Hz的低频范围内变化明显. 这是由于低频段的谱线主要是由与劣化直接相关的电导和极化损耗组成的[15]： 水分含量增加， 油纸绝缘样品的电导率增加， 造成电导损耗随之增加； 另外， 水分增加也对油纸绝缘样品中的LFD传输过程产生影响[16].

对于不同水分含量的复电容实部测量数据， 分别按照在第2.2节所述步骤进行了插值拟合以及积分计算， 得到对应的剔除电导后弛豫损耗谱线. 图3 为不同含水率样品的测量复电容虚部与剔除电导后的复电容虚部谱线. 由图3可以看出， 剔除电导后的极化损耗曲线的峰型特征随着水分增加而逐渐消失. 水作为强极性分子， 含水率增加， 介质中的偶极子数量增加， 不同偶极子之间的排列更加规律， 因此簇间的耦合作用增强， 损耗峰的低频侧谱线趋于平坦[17]. 根据式(4)， 测量谱线减去极化损耗谱线获得直流电导损耗谱线， 并通过最小二乘直线对其进行拟合， 如图4所示.

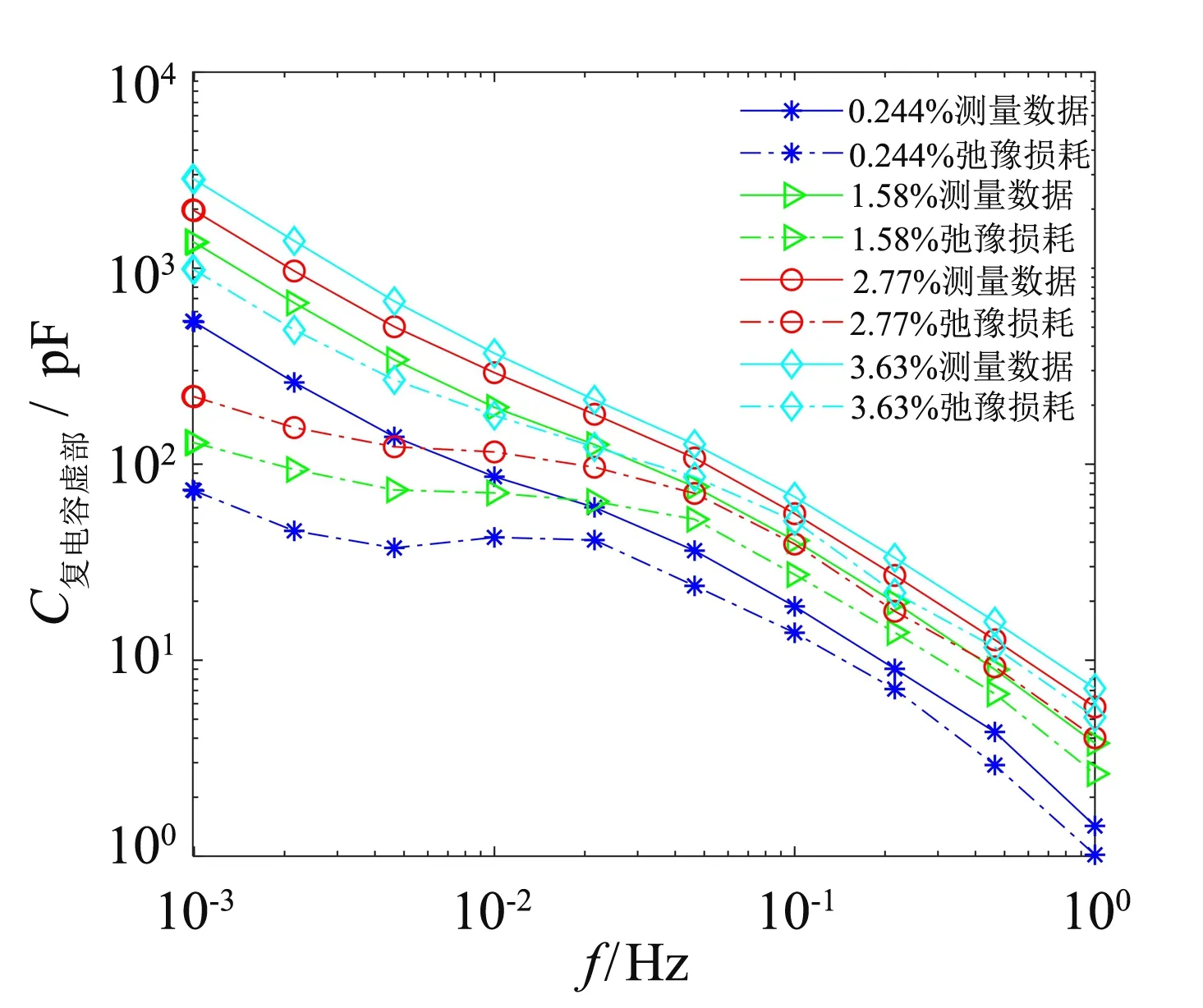
图3 测量复电容虚部与剔除电导后的复电容虚部谱线

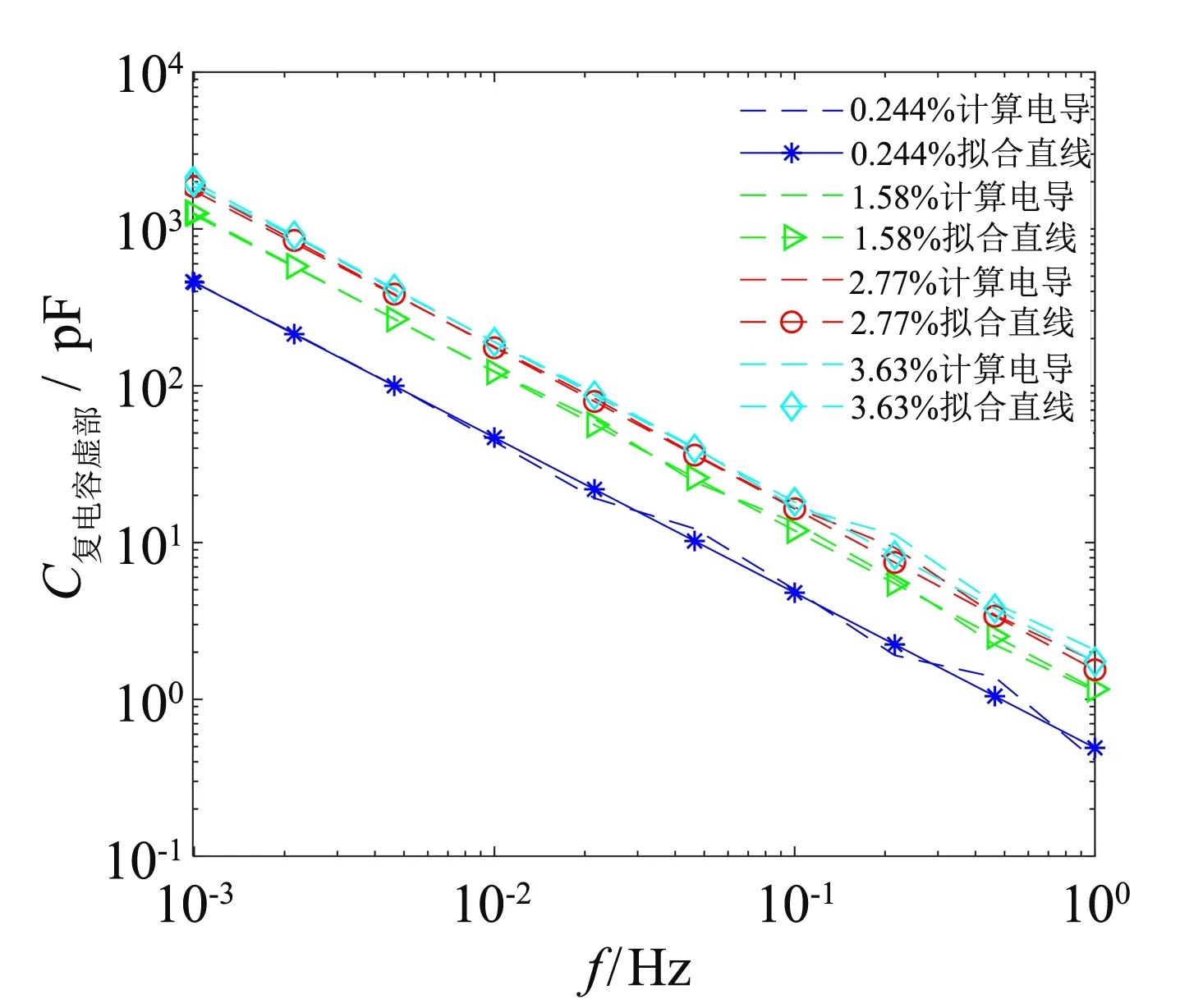
图4 直流电导损耗谱线和拟合直线

电导计算结果和拟合公式如表1所示， 可以看出在双对数坐标系的斜率均约等于-1， 与直流电导频域特性相一致， 证明了本研究所提出电导计算方法的有效性和准确性.

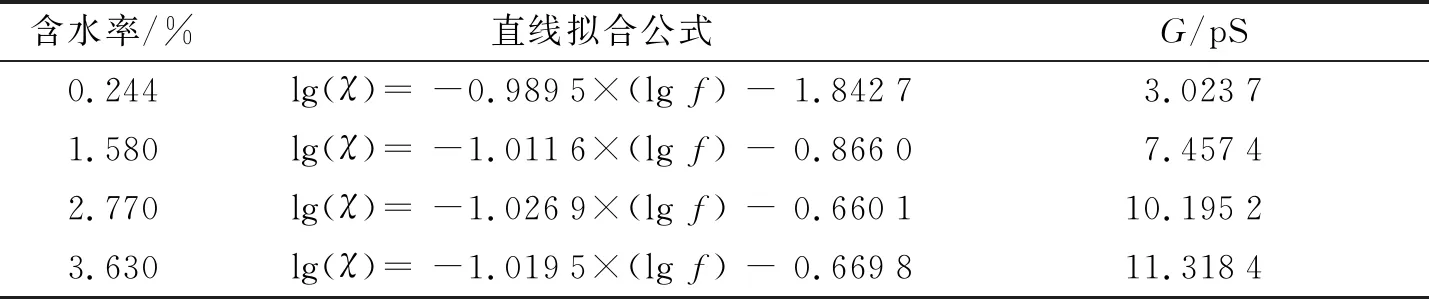
表1 直线拟合公式和电导计算结果

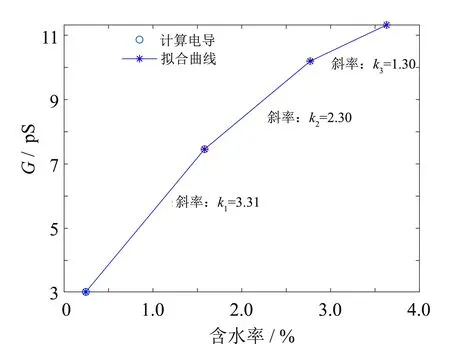
图5 含水率-电导拟合曲线

从表中可以发现， 随着水分含量的增加， 计算出的电导也随之增加. 这是由于水分是绝缘纸主要离子来源[18]， 而形成电导过程的主要原因是电子的势垒跳跃运动[10]： 在施加的电场的作用下， 电子连续穿过陷阱势垒， 最终到达电极. 当油纸绝缘样品的水分含量增加时， 参与势垒跳跃运动的离子随之增加， 因此电导过程增强， 电导增大. 为了更直观地研究受潮后油纸绝缘样品的电导饱和特性， 绘制了含水率-电导曲线， 并计算斜率， 如图5所示.

由图5可知， 随着含水率增加， 含水率-电导曲线的斜率减小， 说明油纸绝缘样品受潮后会逐渐达到饱和状态， 水分子自身解离出H3O+和OH-以及溶解于水分子的杂质离子逐渐达到最大值， 电导趋于饱和.

4 结论

本研究在油纸绝缘样品的频域测量介电谱基础上， 提出了基于Kramers-Kronig关系的油纸绝缘直流电导计算方法. 通过对不同水分含量的油纸绝缘样品的FDS实测谱线的电导计算， 验证所提出方法的有效性和准确性. 此外， 利用Kramers-Kronig关系将复电容虚部谱线分解得到电导损耗谱线和弛豫损耗谱线， 对于区分电导过程和极化过程有重要意义， 为后续研究低频范围的微观介电响应过程奠定基础.