恒星观测与新天文学革命
2021-04-23王广超郑涵
王广超 郑涵
摘 要 近代欧洲的新天文学革命主要得益于古希腊时期即已成熟的偕日升观测技术以及黄道十二宫为主的坐标体系。古希腊天文学家对岁差现象有深刻的认识,使得后来的第谷能够创建一套更为精密的恒星表,为开普勒发现椭圆定律奠定基础。而古代中国的恒星观测采用了冲日法和以二十八宿为主的坐标体系,由于缺乏对岁差效应的准确的理解和解释,中国古代天文学理论在根本上是不确定的。
关键词 恒星观测 托勒密 第谷 开普勒 天文学革命
中图分类号 N09∶P1
文献标识码 A
收稿日期:2021-08-06
作者简介:王广超,1975年生,北京人,理学博士,中国科学院大学人文学院科学技术史系教授,研究方向为天文学史;郑涵,1998年生,广东潮州人,中国科学院大学人文学院科学技术史系硕士研究生,研究方向为天文学史。
基金项目:国家自然科学基金面上项目(项目编号:11973043);中央高校基本科研业务费专项资金。
① 康德在《纯粹理性批判》第2版序言中指出:“这里的情况与哥白尼最初的思想是相同的。哥白尼在假定整个星群都围绕观察者旋转,对天体运动的解释就无法顺利进行之后,试一试让观察者旋转而星体静止,是否可以更为成功。”这被认为是康德自认为开辟了形而上学领域内的“哥白尼式革命”的文本依据。参见[1]。
提起科学革命,我们一般会想到哥白尼革命,正是哥白尼(N. Copernicus,1473—1543)提出日心地动说,改变了人们长久以来笃信的地心学说。18世纪的哲学家康德甚至把自己的认识论描述成了“哥白尼式革命”①。但是,近代天文学革命并非是哥白尼而是由开普勒(J.Kepler,1571—1630)实现的。因为,尽管哥白尼提出颠覆性的日心-地动学说,但他依然使用亚里士多德(公元前384—322)的概念如常规运动、天球等建构其体系,甚至可以说,哥白尼是“根据亚里士多德的原则否定了托勒密(C. Ptolemaeus,100—170)的宇宙模型”([2],页62)。开普勒则不同,他提出了行星运动三定律,更重要的,由于行星的运动轨迹是椭圆而非正圆,开普勒建构出了一套全新物理学理論来解释行星运动。开普勒何以能发现行星运动三定律?一般认为是基于第谷(Tycho Brahe,1546—1601)对火星运动的观测,正如《新天文学》(New Astronomy)完整书名“根据因果关系、或根据尊贵的第谷对火星运动的观测而导出的天界物理学所作的新天文学”Reasoned from Causes, or Celestial Physics, Treated by Means of Commentaries on the Motions of the Star Mars, from the Observations of the noble Tycho Brahe.表述的那样。而实际上,一个更具决定性的因素是欧洲长久以来形成的恒星观测技术。
本文尝试从古代的欧洲与中国在恒星观测技术方面上的不同入手,探讨何以是西方而非中国发生新天文学革命,并追溯至古希腊时期确立的恒星观测技术。第谷在古希腊恒星观测的基础上创建出一套精密的星表,是开普勒提出椭圆定律和面积定律的经验基础。然而,中国的恒星观测技术并不支持产生像西方那样的革命,主要是由于缺乏一个恒定不变的坐标体系,以及对岁差问题的透彻理解。
一 新天文学革命
哥白尼在天文学的主要贡献是提出日心-地动模型。实际上,他对恒星位置的测算以及恒星表的编订非常重视,甚至将“恒星表”至于首位,认为准确的恒星数据是研究行星运动的基础。《天球运行论》(On the Revolutions of the Heavenly Spheres)中有一张完整的恒星表,主要基于《至大论》(Almagest)此书名有学者译为《天文学大成》,是古希腊托勒密在约公元140年编纂的一部数学、天文学专著。中的星表改编而成[3],将其中恒星的黄经值减去6度40分,而黄纬不变。在编制星表过程中,哥白尼曾利用“浑仪”(armillary sphere)对托勒密的数据进行复验,发现有不少偏误,但他只对其中的狮子座α(Regulus)和室女α(Spica)的数据做了些许调整[4]。
哥白尼认为《至大论》最主要的问题是未给予恒星表以足够重视。在《至大论》中,恒星表被置于第7章的第5节到第8章的第1节之间,位于日月运动理论之后,潜在的理由是恒星的位置坐标是以一些在黄道上的具体恒星,如狮子座α(Regulus)、室女座α(Spica)(即距星)为根据的,这些距星的位置则依据太阳以及月亮的位置而算定。哥白尼将“计算恒星的位置,设置恒星星表”一节放在了《天球运行论》的第二部分,主要讨论天球坐标系的各种圈:地平圈、黄道圈、赤道圈,以及黄赤交角和基本坐标系问题。很显然,哥白尼试图将恒星数据作为更基本的参照对象。从这一安排中哥白尼似乎已隐约预见到,将来天文学的真正突破将寄托于更精准地测定恒星位置[5]。
尽管哥白尼提出了颠覆性的日心地动学说,但他的理论是在传统的古希腊宇宙论基础上搭建起来的。他认为行星附着在天球上随天球一起旋转,天界的物体做常规匀速圆周运动。这些理论来自亚里士多德,而哥白尼试图革新的其实是托勒密的理论,尤其是其中的偏心-等速点模型(equant)。在他看来,偏心等速点(equant point)既不是本轮的中心,也不在本轮上,却是行星运动的参照点,而这一点本身没有实际的物理意义,这在哥白尼看来不能令人满意。正是由于认识到偏心等速点模型的缺陷,哥白尼试图找到一种更为合理的模型[6]。
开普勒之所以提出行星运动三定律、发表《新天文学》,部分原因要归于他获得了第谷的观测数据。《新天文学》出版于1609年,1600年开普勒受邀协助第谷做天文学研究。早在1596年,开普勒曾出版《神秘的宇宙》一书,试图论证哥白尼的日心说是正确的,尽管此书有不少错误,却充分地展现了其在数学方面的才能,而这正是他受到第谷青睐的主要原因。第谷希望开普勒根据他毕生心血积累起来的观测数据建立“日心地不动”学说,即介于哥白尼和亚里士多德之间的调和模型:太阳为行星运动的中心,日月围绕地球做匀速圆周运动。开普勒起初在构建模型时却曾依照第谷体系,后来却发现它与其观测数据有较大的差误,最终他不得不放弃之前的承诺。
基于第谷的观测数据,开普勒于1602年完成面积定律的构建,期间,他主要使用第谷遗留的火星在冲点位置时的数据,计算火星轨道的参数。所谓“冲”,就是火星和太阳的经度正好相差180°,或者说火星、地球和太阳三者正好处于一条直线上,地球在中间,火星和太阳分处两边。1580—1600年,第谷留下10个这样的观测记录,总体精度达到2分。开普勒选取了其中4个,其年份分别是:1587、1591、1593和1595年。经过计算,他发现轨道的中心不在太阳到偏心匀速点之间,尽管这一结果可以得到观测支持,但用另一些观测数据复验时却发现了偏差。于是,开普勒重新回到“托勒密假设”计算距离定律,即计算行星运动的速度和它到太阳的距离之间的关系([2],页270)。但正圆与实际观测到的数据不合,在圆周的侧面要小一些。在用了两年时间的多次尝试之后,开普勒终于发现卵形比较合适。进而,他又将卵形调整为椭圆模型[7]。
从表面上看,开普勒是基于第谷的火星观测数据得出行星运动的面积定律和椭圆定律。而实际上,开普勒所依据的火星冲位置的精确数据是建立在准确测定恒星位置之上的。开普勒刚进入第谷的研究团队时,曾被派去辅助第谷的弟子隆戈蒙塔努斯(C. S. Longomontanus,1562—1647)解决火星运动问题,而这也被认为是开普勒以火星运动为切入点研究行星运动的主要原因。开普勒甚至还庆幸自己最初就找对了方向,否则可能永远不能发现椭圆定律。
第谷自16岁起就开始进行恒星观测,至51岁时,大概经历了3个阶段:前6年在莱比锡所做的工作价值不大;之后的7年,观测结果虽不成熟,但大致可用;其28—50岁这21年间,他用力最勤,装备最精,观测精度最高。第谷尽其所能,细致地测定了所有肉眼可见的恒星位置,甚至包括六等星。他所测量数据的总体精度已达一弧分,有些甚至已到半弧分。为提高观测精度,他还改进了一些观测仪器,常用的测星仪器是一架“大六分仪”。六分仪是一架看上去有些像圆规的测量仪器,圆规的脚是由两根长长的木条做成的“臂”,两臂之间安有弧形的刻度盘。使用时,观测者把两臂分别瞄准要测量的两点,然后在刻度盘上读出所对应的弧度。在第谷的时代,六分仪是通用仪器,往往用来测量恒星之间的距离、恒星的方位以及地平高度。但第谷却只用六分仪来测量恒星的地平高度。因此,他把仪器的一条臂固定在水平的位置上,从而基本排除由于观测者手臂或身体的抖动而带来的测量误差。仪器的另一条臂可以绕固定端点活动,臂上有两个视窗,观测者可以用此校准视线,捕捉观测目标。一旦确定,在臂的远端的弧形刻度盘上即可读出该目标的角高度。第谷用大六分仪测的精度高达24弧秒,而此前托勒密的精度大概在10弧分左右,哥白尼的在6—10弧分,从一定意义上说,第谷将观测恒星的精度提高了20多倍([2],页167—168)。这就为准确地观测和记录火星“冲”的位置打下了坚实的基础,而这些数据正是开普勒建构椭圆轨道的经验基础。
二 古希腊的恒星观测
第谷一直致力于改进的观测方法早在古希腊时期就已形成。可以说,正是古希腊天文学传统使得第谷对恒星观测的改进成为可能。欧洲天文学以黄道坐标系为主,十二宫为基本坐标。最初的十二宫为星象,至古希腊时期,十二宫已成为固定于黄道的基本坐标。总体看来,《至大论》中所载恒星测算可以分为两步。第一,确定位于黄道上的距星的准确位置;第二,通过浑仪测定某星相对于诸距星的位置([8],pp.251—253)。
关于第一步,《至大论》给出两种方法,均与月亮位置的推算相关。第一种方法可以称为“月食法”,因为月食时太阳正好处于与月亮相距180度的角度上,因此:
距星的经度=太阳在月食时的经度+从月亮到该星的经度差+180°(1)
(1)式右侧第一项可通过日、月运动算法计算求得,第二项通过浑仪测得。此法在托勒密前的喜帕恰斯(Hipparchus, 公元前190—120)时期即已形成,需在发生月食时才能测算。为了打破此限制,托勒密发展出另一种方法,对应公式如下:
距星经度=太阳所在经度+从太阳到月亮的经度差+从月亮到所测星的经度差(2)
(2)式右侧前两项,有关太阳和月亮的经度,需要由天体运动算法计算而得。而第三项,需通过浑仪测定。或许正是这个原因,《至大论》中的恒星表位于月亮理论之后。而这也正是后来的哥白尼所批判的问题之一。然而在上面两个公式中,还需加入月亮运动的修正值,主要包括两项:首先是月亮东行的修正,因为月亮一天大概运动12°,每小时大概0.5°,这一变量不可忽略;另外,需考虑月亮的时差,也就是从地球表面和地心观测的差异。《至大论》不但讨论测量恒星的方法,还给出了测量实例,在第七章的第2节讨论了测定狮子座距星经度的方法([8],pp.254—255)。
以上这些测算方法,是以岁差理论作为基础。西方天文学之所以能在近代发生天文学革命,另一个主要原因是发展出一套精致的岁差理论。可以肯定的是,托勒密保留了关于喜帕恰斯有关岁差方面的工作。《至大论》明确指出,喜帕恰斯发现室女座α(Spica)的位置应该是在秋分点偏西6°,而在此之前提莫卡里斯(Timocharis,公元前320—260)观测到此星的位置在秋分点偏西8°位置。关于提莫卡里斯,我们所知甚少,现在只能从《至大论》中获得些许信息:他被认为是古希腊的系统天文观测的奠基者,生活在亚历山大里亚,其主要工作集中在公元前290—280年间。喜帕恰斯对岁差的判断主要基于他和提莫卡里斯的几次月食记录,这些数据记录在《至大论》中。其中还提到:至点和分点相对于恒星有一个恒定的西退,速度不超过每百年1度。
托勒密采用了喜帕恰斯的数据,即每百年1°的东移。除此之外,托勒密对狮子座(Regulus)也做了细致的观测,主要基于月食观测数据。他发现,相较于喜帕恰斯记录的狮子座位置,他看到的似乎相对于至点有一个2°40′的东移,而他的观测时间与喜帕恰斯之间相差265年,这就很接近百年差一度的移动速度。但与喜帕恰斯不同,托勒密认为整个恒星天球在东移,不仅是黄道上的至点和分点,所有恒星均有一个整体的东移倾向,速率约为百年1°。為探究恒星天球究竟是以黄极还是赤极为轴,托勒密引用由提莫卡里斯与喜帕恰斯的观测数据,最终确定恒星东移不是沿赤道而是黄道。这一理论后来被纳入到天球宇宙论,即诸恒星附着在恒星天球上,以100年1°的缓慢速率东移。
由此可见,托勒密时代确定了准确测定恒星的基本方法,发现恒星运行的基本规律。尤其重要的是,由于发现恒星东移规律,使得其后延续的数据可以不断更新和改进。也正因此,第谷发现了不少前辈观测方面的问题,并在改进中提升了观测精度,这些为天文学革命打下了坚实的基础。中国天文学的发展则与之不同,也体现在恒星观测方法以及对恒星运动规律的认识方面。
三 古代中国的恒星观测
科学史家席文(Nathan Sivin)先生指出,不同文明的人用几乎相同的方法研究同样的星空,其主要目的是为了搞清楚何时、何地发生了那种天象,但他们对星空的划分以及这些划分所暗含的基本理念是不同的,也正因此,不同文明创造了自己的星空[9]。西方天文学采用了十二宫的坐标体系,至托勒密时期,十二宫主要是对黄道而非星象的划分。而之所以形成以黄道为主的坐标体系,这与古希腊人的观测星空的方法有关。希腊人主要采用偕日法观测星空,包括观察恒星偕日升和偕日落,即观测黄道附近的恒星在日出或日落后瞬间的升落[10]。
而中国古代天文学则以赤道坐标为主,主要以二十八宿为基本坐标系。准确地说,中国古代天文学采用的是一种北极—赤道坐标体系,北极居核心地位,赤道只起辅助作用。时圈从北天极向周围展开,提供一种按时圈与赤道相截的点来划分的赤道分区体系,即所谓的二十八宿。李约瑟(Joseph Needham,1900—1995)认为:中国古代的北极-赤道体系与小宇宙-大宇宙的思想背景有关,因为拱极星的上中天可用来指示看不到的宿的方位,《史记·天官书》中就有明确表述,如“杓携龙角,衡殷南斗,奎枕参首”其含义是角宿的位置可以通过北斗七星斗柄的最后二星的位置确定,而斗魁的“顶”和“底”(即天权、天枢、天玑、天璇)的延长线与参宿相交[11]。这套体系的建立与古代中国的观测方法有关,采用了与古代西方完全不同的冲日法,主要观测永远不升不落的极星和拱极星,也正因此古代中国的天算理论与子午线密切相关。二十八宿的界限一经划定,在理解了天球的周日运动之后,由拱极星的上中天和下中天即可确定去天球赤道上每一点的位置。进而,通过望月时月亮的位置确定太阳在恒星间的位置,确定太阳和恒星的坐标关系。
与偕日法相比,冲日法有其优势,主要由于地平线上的雾或其他大气现象,偕日升和偕日落的准确时间可能难以确定。而冲日法最大的问题是忽略了对黄道体系的建构,因而难以对岁差现象有准确的理解由于岁差效应,北极点在缓慢移动,与之相应,如以恒星为参照,黄赤交点在沿黄道缓慢西退,从而导致恒星年与回归年的不同,这就是中国古人所谓的岁差。。由于缺乏黄道体系的认识和使用,古代中国人缺乏对此现象的整体理解,尽管历史上不乏对岁差现象的准确观测,但都是比较零散的,缺乏整体性考虑。
古代中国历算家一般将岁差的发现归之于东晋的虞喜(约270—345)。主要依据是《大衍历·历议》中的“其七日度议曰:古历,日有常度,天周为岁终,故系星度于节气。其说似是而非,故久而益差。虞喜觉之,使天为天,岁为岁,乃立差以追其变,使五十年退一度”([12],页2181)。虞喜是通过冬至日中星的观测而发现岁差的。他把自己所做观测结果与前人的记录进行比较,发现冬至日黄昏出现于天空正南方的星宿明显不同,唐尧时代冬至日昏中星是昴宿,而到了他的时代则变成了壁宿,虞喜把这种变迁归因于冬至点连续不断地西移。也就是说太阳在冬至所躔宿度逐渐西退所造成的。
在虞喜以前就有人注意到不同时代所测冬至点太阳所在宿度不同[13]。先秦时期《颛顼历》记载冬至点在牵牛初度,西汉初年编制的《太初历》虽仍沿袭了这个数值,但刘歆在《三统历》中对此说颇有怀疑,他时而说“冬至,日月在建星”,時而认为在牵牛初度,甚至还说冬至“进退牛前四度五分”。东汉时贾逵根据元和二年(85)至元元年的实测,确定“冬至日在斗二十一度四分度之一”。但贾逵只是对冬至点的宿度做了改正,没有意识到冬至点是运动的。从贾逵到虞喜间隔二百多年,冬至点又西移四度左右,虞喜之后的姜岌运用月食冲检日度法,才精确地测得公元384年前后冬至点太阳已在斗十七度。
自东晋以来,中国长期用观测昏旦中星的方法测定冬至宿度,这种方法必须有精确的时刻,若测量中星有差,则结果不准。南北朝时梁武帝大同九年(543)虞邝对此有论:
然日之所在难知,验以中星,则漏刻不定。汉世课昏明中星,为法已浅。今候夜半中星,以求日冲,近于得密。而水有清浊,壶有増减,或积度所拥,故漏有迟疾。臣等频夜候中星,而前后相差或至三度,大畧冬至远不过斗十四度,近不出十度。又以九年三月十五日夜半,月在房四度蚀。九月十五日夜半,月在昴三度蚀,以其冲计冬至,皆在斗十二度,自姜岌、何承天所测,下及大同日已却差二度。([12],页2198—2199)
由上可见,中星法其实是冲日法的一种具体应用,这在根本上与古希腊所用的偕日法不同。由于难以测定准确的夜半时间,不确定因素太多,古代天文家对岁差发现迟疑不定,甚至在积累充分证据后,还不敢承认。比如,唐初李淳风修历时虽已注意到岁差现象,出于政治方面的考虑,在其所主持编修的《麟德历》还未引入岁差。另外,他主持编修的晋、隋两代的《天文志》和《律历志》中对东晋虞喜发现岁差现象也只字未提。
继虞喜之后,何承天(370—447)给出新的岁差值,大约每百年一度,与希帕恰斯-托勒密的数值比较接近,或许是受到了西方的影响[14]。然而,何承天并没有把岁差应用到历法中去,在他编制的《元嘉历》中仍采用日数等于周天度数的陈规。中国历史上,第一个把岁差引进历法的是祖冲之(429—500),他在《大明历》里把岁实同周天度区分开来,又把自己“参以中星,课以蚀望,冬至之日在斗十五”的结论与姜岌测冬至日在斗十七的结果比较,认为“通而计之,未盈百载,所差二度”,定出岁差值为“四十五年是一个月差一度”。“令冬至所在,岁岁微差”。使得日宿度和节气的推算更加准确。祖冲之的做法遭到朝廷显贵的非难,坚持“古历冬至,皆在建星”,以此指责祖冲之引进岁差,是“虚加度分,空撤天路”“诬天背经”。祖冲之专门写《驳议》一文据理驳斥。此后许多历算家仍拘于陈法,不敢用岁差。
如以恒星为参照看黄赤交点或冬至点,其缓慢的西退应沿黄道而非赤道。祖冲之及其以前的历算家所论多以赤道为宗。隋刘焯(544—610)首先提出了黄道岁差的概念,认为推算日月与五星的行度应该依据黄道度才更简便和精确。然而,尽管刘焯的方法更科学,但由于缺乏充分的证据作为支撑,未得后世传承。唐初傅仁均造《戊寅历》引入岁差,遭到历算博士王孝通的指责。李淳风甚至依据《尧典》四仲中星的内在矛盾,否认岁差现象的存在。
真正把岁差作为一个重要的历算概念固定在历法中得以流传的是中唐时期的一行(683—727),其主持编订的《大衍历》为后世所宗。一行在隋刘焯基础上重建岁差概念,继承刘焯推算黄道日度的原理,主张“若上考往古,下验将来,当据岁差,每移一度,各依术算,使得当时度分,然后可以步三辰矣。”但一行并不认同刘焯关于黄道岁差的概念,仍以推算赤道日度为据,计入岁差。《大衍历·历议》中有如下解释:“所谓岁差者,日与黄道俱差也,……黄道不迁,日行不退,又安得谓之岁差乎?”由此可见,一行给出岁差的运动学机制,即黄道沿赤道西退。自此之后的历法直到《大统历》为止,都沿袭了《大衍历》的传统。如《授时历》取赤道岁差为1分50秒,而黄道岁差为1分39秒,后者是赤道岁差值在黄道上的投影分量。
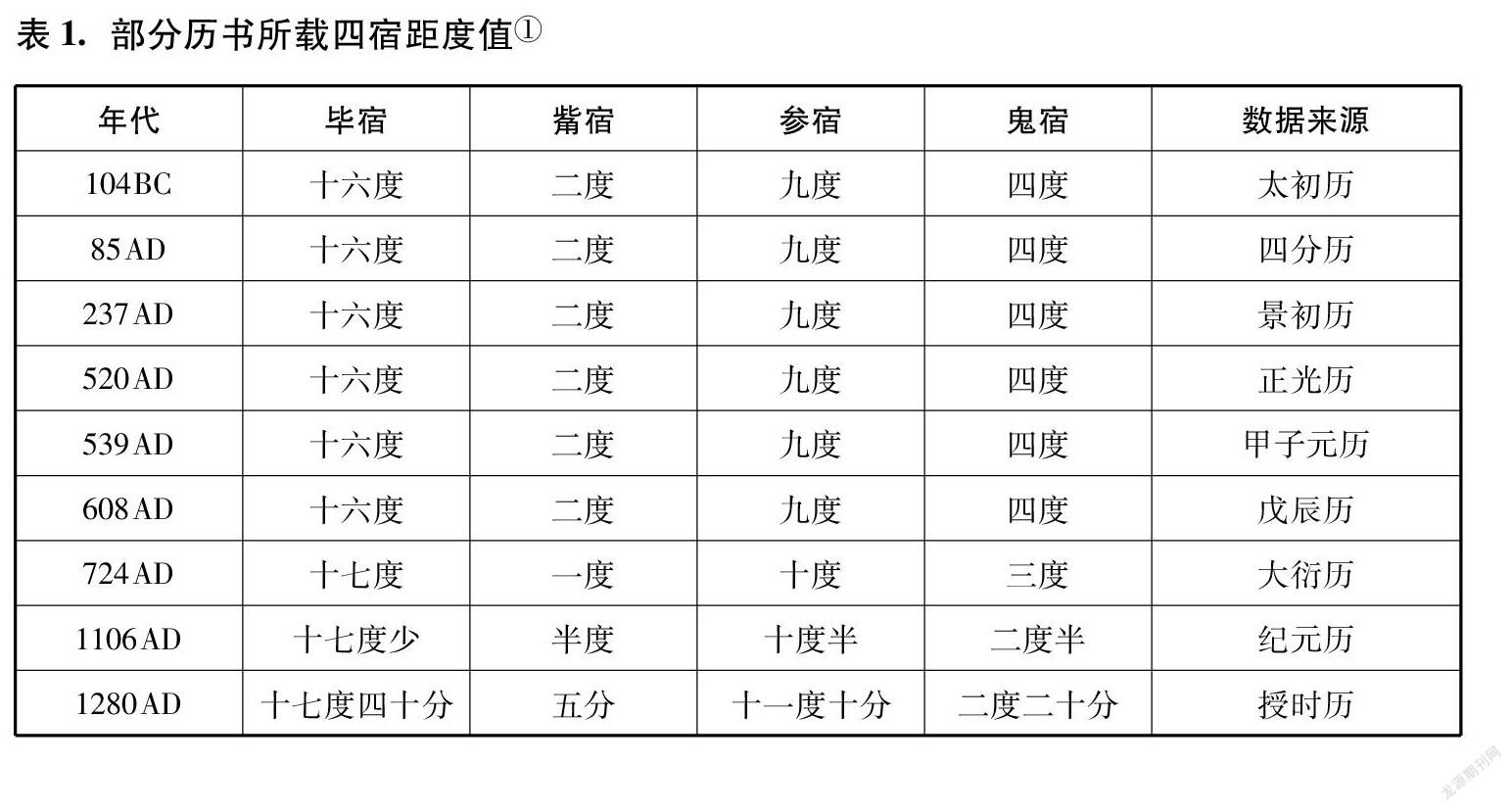
一行的岁差概念之所以产生如此影响,主要是由于他重新厘定了二十八宿的距星,测量了距度和去极度,与古法不同。唐初贞观年间,李淳风也曾注意到二十八宿距星相较古测已有变化。但在这个问题上,李氏比较保守,在其主持修撰的《麟德历》中,依循旧法。一行发现二十八宿中毕、訾、参、鬼四宿的距度与古代不同([12],页2225)。表1对部分历书所载四宿距度值进行比较。
另外,一行还发现二十八宿去极度的变化,即从牛宿到井宿,古大今小,其间稍有差异的是女宿(古小今大)和危宿(古今相同);从鬼宿到斗宿,古小今大,其中稍异者仅有鬼宿(古今相同)。一行将自己观测的二十八宿去极度的数据(今测)与《石氏星经》中的(旧测)相比,发现上述的变化规律。《石氏星经》收录于瞿昙悉达所著的《开元占经》当中,大约成书于开元六年(718)前后,对一行来说是非常重要的参考。
一般认为,古希腊人由于亚里士多德的天球理论,认为天界的变化是不可接受的,因而他们对一些明显的异常天象,如超新星和黑子等,都视而不见,或见而不录。所以,从古代西方的天象记录中很难找到这些违背常理的记录。而古代中国由于没有类似西方的宇宙论对天文观测的约束,加之异常现象对星占而言有重要意义,因此许多异常现象被忠实记录下来。尽管如此,中国古代天文学中也存在视而不见、见而不述的情况,比如岁差,其实早在汉代时即已發现冬至点太阳所在宿度已与之前春秋时期有很大不同,但直到东晋虞喜(281—356)才指出存在回归年与恒星年不同的岁差现象。与之相应的,二十八宿距星,由于岁差效应,也在不断地移动。但从汉至唐700多年的时间里,没有人提出调整,直到中唐时期的一行方才改观。之所以有如此差异,是因为希腊人更加关注发现天体运行规律。岁差现象,尽管短时期看并不明显,但时间一长,即呈现出规律性的变化。岁差理论后来被纳入到天球体系之中,恒星天球的主要运动。而中国古代天文学,尽管对变化性现象非常关注,但对于一些固有观念,例如年的概念,二十八宿的距星等,是不容有变的。
四 结语
袁敏等曾以“如果开普勒是中国人”为题讨论中西方数理天文学的差异,认为中国古代数理天文学偏重数值算法的创造,缺乏对几何模型的建构,而以古希腊为源头的欧洲天文学则正好相反。她们认为,对于熟悉圆锥曲线并强调几何模型的人来说,可以根据一行的太阳视运动中心差算法推导出椭圆模型[15]。言下之意,一行的太阳视运动算法逻辑上可以推演出椭圆模型,导致中国古代天文学家未发现椭圆定律主要原因是中国古代历算家缺乏圆锥曲线的认识。但是,开普勒并不是根据太阳的视运动,而是基于火星运动数据构建了行星的椭圆模型。而数学上偏心等速点模型和椭圆模型是等价的,也就意味着,根据《至大论》中任何一个行星的运动模型在理论上都可以推演出椭圆模型。那么何以开普勒未根据其他行星的运动发现椭圆规律,庆幸从火星研究中发现了新天文学的曙光呢?我们还是要回到恒星观测数据方面,可以肯定,如果没有第谷的恒星观测数据,开普勒是无法发现“真实”的宇宙结构的。
恒星观测是古代中西方天文学的一个主要区别,体现在观测方法及所用主要坐标系这两方面。古希腊采用偕日法,确立了以黄道而非恒星为主的坐标体系。而古代中国采用的是冲日法,更关注极星和拱极星的位置变化,致力于建立一套以北极-赤道坐标系为主,以具体的恒星背景作为参照的坐标系。由于岁差效应,全天恒星沿黄道有一个东移,致使北极和二十八宿距星在长时段内是运动的。由于缺乏对岁差本质的认识,中国古代的恒星观测非常混乱。中国古代天算家往往采取含糊其辞的应对策略:一方面通过不断观测确定准确的恒星背景;另一方面为了寻求与古代传统数据的契合,不得不迁就一些陈旧的观念或说法。而西方天文学建立了以黄道坐标为主的坐标系,采用十二宫坐标系,黄道坐标固定不动,以此为参照,认识到恒星沿黄道东移的规律,这就为整个数理天文学的发展提供了坚实的基础。
古希腊天文学家很早就发现恒星东移的规律,表面上具有一定的偶然性,即恰好古希腊天文学家采用了从古巴比伦继承的黄道坐标系,而诸恒星正好存在一个沿着黄道的运动。但是实际上,托勒密等在得知恒星有缓慢的东移运动后,曾探寻这种运动究竟是沿着赤道还是黄道运动,即寻找这种缓慢运动的轴。在找到确凿的证据后,最终才确认恒星是沿黄道东移[16]。古希腊时期发现的恒星运动的确定性,不仅为行星运动提供了准确的参考,更重要的,使得后来的观测可以不断地对前人进行修正。比如,哥白尼之所以对托勒密星表提出批判,主要是他已得知伊斯兰天文学家对托勒密星表的修正。而第谷正是在改进仪器的基础上,对托勒密的星表做了完整的修正和补充。恒星数据的确定性还使得第谷对托勒密星表数据是否真的由托勒密本人所做产生了怀疑。因为尽管托勒密宣称其星表中的数据是他本人所测,但第谷怀疑,《至大论》中的数据是从喜帕恰斯星表数据改编而来的,即黄纬保持不变,而黄经按照每百年差一度做一定的调整。当然,第谷并没有找到确凿的证据,重要的是很难找出喜帕恰斯留下的星表数据。因此,这一争议持续四百多年,至今尚无定论。尽管如此,古代西方恒星数据的确定性,实际上给后人推算往古提供了可能性。因此,托勒密时期所确立的星表数据是可以证伪的,这也就使得后人可以在前人的基础上不断地提高测算经度,更新数据。最终开普勒基于第谷更为准确的星表得出了行星运行的规律,开启了新天文学的篇章。
参考文献
[1] 康德. 纯粹理性批判(注释本)[M]. 李秋零(译注). 北京: 中国人民大学出版社, 2011. 11.
[2] 吴以义. 从哥白尼到牛顿: 日心说的确立[M]. 上海: 上海人民出版社, 2013.
[3] Grahoff G. The History of Ptolemys Star Catalogue[M]. New York Berlin Heidelberg: Springer-Verlag, 1990. 23.
[4] Swerdlow N M, Neugebauer O.. Mathematical Astronomy in Copernicuss De Revolutionibus[M]. New York Berlin Heidelberg Tokyo, 1984. 121—123.
[5] Duncan A M.. Copernicus: On the revolutions of the heavenly spheres. A new translation from the Latin with introduction and notes[M]. David & Charles: Newton Abbot London Vancouver, 1976. 103—139.
[6] Copernicus N.. Three Copernican Treatise[M]. translated by Rosen E. Dover Publications, 1959. 57.
[7] Kepler J.. New Astronomy[M]. translated by Donahue W H. Cambridge: Cambridge University Press, 1992. 575.
[8] Evans J.. The History and Practice of Ancient Astronomy[M]. New York and Oxford: Oxford University Press, 1998.
[9] Sivin N.. Granting the Seasons, the Chinese Astronomical Reform of 1280, With a Study of Its Many Dimensions and an Annotated Translation of Tis Records[M]. Springer, 2009. 7.
[10] Needham J.. Science and Civilisation in China. V3 Mathematics and the Sciences of the Heavens and the Earth[M]. Cambridge University Press, 1959. 229.
[11] 朱文鑫. 《史記·天官书》恒星图考[M]. 上海: 商务印书馆, 1934. 11—12.
[12] 欧阳修. 新唐书·历志[A]. 历代天文律历等志汇编·第七册[C]. 北京: 中华书局, 1976.
[13] 何妙福. 岁差在中国的发现及其分析[A]. 科学史文集(1)[C]. 上海: 上海科学技术出版社, 1978. 22—30.
[14] 郑诚. 何承天岁差考[J]. 上海交通大学学报(哲学社会科学版), 2007,(1): 50—57.
[15] 袁敏, 曲安京. 假如开普勒是中国人[J]. 自然辩证法通讯, 2008,(1): 69—74.
[16] Ptolemy. Ptolemys Almagest[M]. translated by Toomer G J.. Gerald Duckworth, 1984. 260—261.
Star Observation and the Astronomical Revolution
WANG Guangchao, ZHENG Han
Abstract:Based on the comparison between ancient Chinese and European stellar observation technologies and related theories, this article tries to explain why the new astronomical revolution occurred in Europe instead of China. The conclusion is: the new astronomical revolution in modern Europe mainly benefited from the observation technology of contiguity and the zodiac system during the ancient Greek period. Ptolemy who edited Almagest already had a clear understanding of the phenomenon of precession, which enabled Tycho to create a more sophisticated star catalog which was an important basis for Kepler to figure the planet ellipse law. In contrast, Chinas star observations use the method of opposability and 28 lunar lodges coordinate system. Due to the lack of accurate understanding and explanation of the precession effect, ancient Chinese astronomical theories are fundamentally uncertain. All this does not support an astronomical revolution in modern China like that in Europe.
Keywords:Star observation, Ptolemy, Tycho, Kepler, astronomical revolution
