基于单星测量的星光惯性组合导航

乔 川 ，李 晓 ，庞少龙 ，闫蓬勃 ，李丹凤 ，夏梦绮 ，徐 卿

（1. 北京控制工程研究所，北京100190；2. 空间光电测量与感知实验室，北京100190）

1 引 言

星光惯性组合导航系统利用星光定向仪测量的导航星矢量信息对惯性器件的漂移进行估计补偿［1-2］。相比卫星惯性组合导航方式，星光惯性组合导航系统不需要外部输入，具有更高的安全性，因此在军事领域得到了非常广泛的应用［3-7］。美国三叉戟Ⅱ导弹采用 Draper 实验室研制的 MK6 惯性星光制导系统［6］，命中误差仅为130～185 m，俄罗斯最新一代的战略核打击装备PC-12M 型洲际导弹同样也采用了星惯融合的导航方式，在10 500 km 射程内命中精度优于90 m［7］。

为了减小大气层内杂光的影响，提高信噪比满足全天时的探测需求，全天时星光星惯定向仪一般选择小视场长焦折反式光学系统［8-10］。例如，美国RC-135 侦察机和B-2 轰炸机，都采用了Northrop 公司的 LN-120G，其瞬时视场只有 6′［10］。为了提高白昼观星的探测概率，组合导航系统一般自带转台和摆镜，采用主动寻星的方式工作，每次只跟踪单颗恒星。

近年来，针对星光惯性组合导航系统的研究很多。杨波［11］和张承［12］等人分别利用星敏感器输出的姿态信息实现了星惯组合导航系统的对准及导航算法，但该算法并不适用于只能输出单星矢量的星光定向仪。黄远［13］和张金亮［14］等人分别对基于单星矢量测量的星光惯性组合导航系统进行了误差分析，并提出了相应的对准及导航算法，其定姿精度优于15″（95%CEP）和 8″（1σ），但他们都没有考虑惯导与星光定向仪之间的安装矩阵误差。而实际上，惯导和星光定向仪之间的安装姿态误差可达角分量级，王智［15］等提出的标定方法的标定残差可优于2″，但星光定向仪和惯导之间的姿态标定更为复杂，不仅需要分别标定星光定向仪和惯导相对于各自基准镜的姿态，还需要标定惯导和星光定向仪基准镜之间的姿态矩阵，标定误差在标定过程中传递也会降低标定精度；同时，在实际组合导航过程中星光定向仪与惯导之间的安装姿态由于力热变化也存在漂移，造成导航精度下降，因此实验室标定方法的工程性较差。焦宏伟［16］和郭敬明［17］等分别利用导航星矢量与地心矢量夹角观测值与真值相等的条件建立了状态模型和测量模型，该方法可用来标定惯导与星光定向仪之间的安装误差，但该方法没有考虑到惯性器件的漂移，因此并不适用于天文惯性组合导航系统的导航解算。

本文提出一种基于单星测量的星光惯性组合导航方法。首先根据惯导输出的姿态和位置信息，控制转台和摆镜保证星光定向仪对目标导航星的观测，然后根据惯导的误差模型建立系统状态方程，根据星光定向仪测量的导航星方向矢量建立测量方程，最后利用卡尔曼滤波算法对惯导输出的姿态位置信息进行修正。该方法引入星光定向仪与惯导安装误差作为系统状态量，可在修正导航信息的同时估计星光定向仪与惯导之间的安装误差。

2 初始对准算法

2.1 星光惯性组合导航系统

基于单星测量的星惯组合导航系统示意图如图1 所示，其工作流程如图2 所示。惯导和星光定向仪捷联安装在转台上。首先根据惯导给出的姿态位置信息和惯导与星光定向仪之间的安装姿态，配合导航星库计算导航星在星光定向仪测量坐标系下的方向矢量，并选取目标导航星。根据摆镜和转台的不同，目标导航星的选取方法也不一样。本文选取高度角在9°～45°，矢量投影夹角大于30°且最小的导航星作为目标导航星。然后控制转台和摆镜转动，实现对目标导航星的观测，并得到目标导航星在星光定向仪测量坐标系下的方向矢量，再根据惯导的位置和姿态信息以及惯导与星光定向仪之间的安装姿态，得到目标导航星在导航坐标系下的方向矢量信息。最后根据惯导的误差模型建立系统状态方程，以方向矢量误差作为系统测量参数建立测量方程。利用卡尔曼滤波算法对惯导输出的姿态位置信息进行修正，在修正导航信息的同时对星光定向仪与惯导安装误差进行估计。

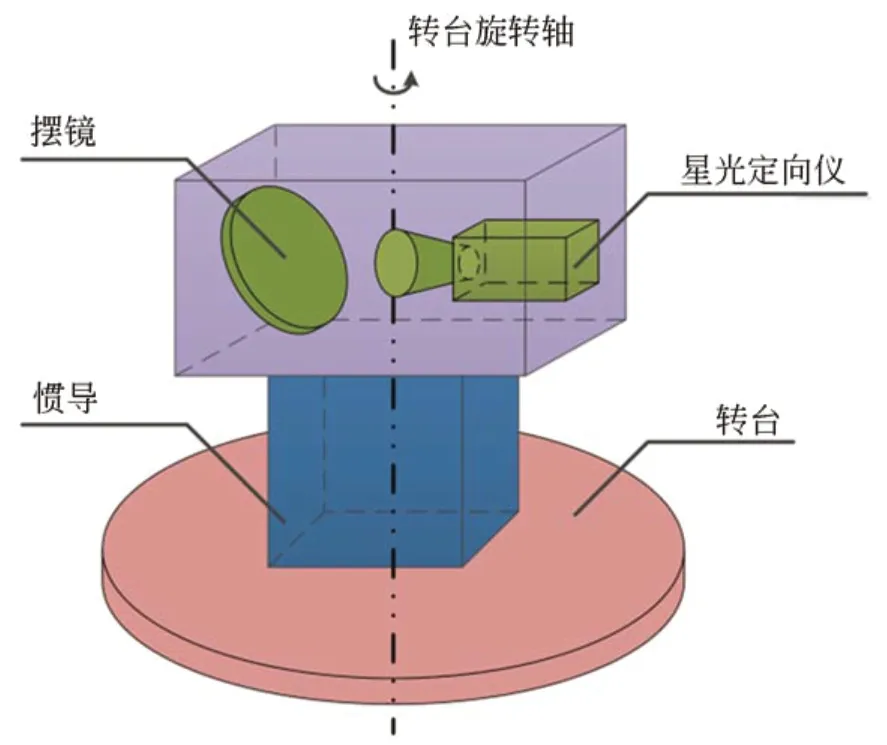
图1 基于单星测量的星光惯性组合导航系统示意图Fig.1 Schematic of starlight-inertial integrated navigation system based on single star vector

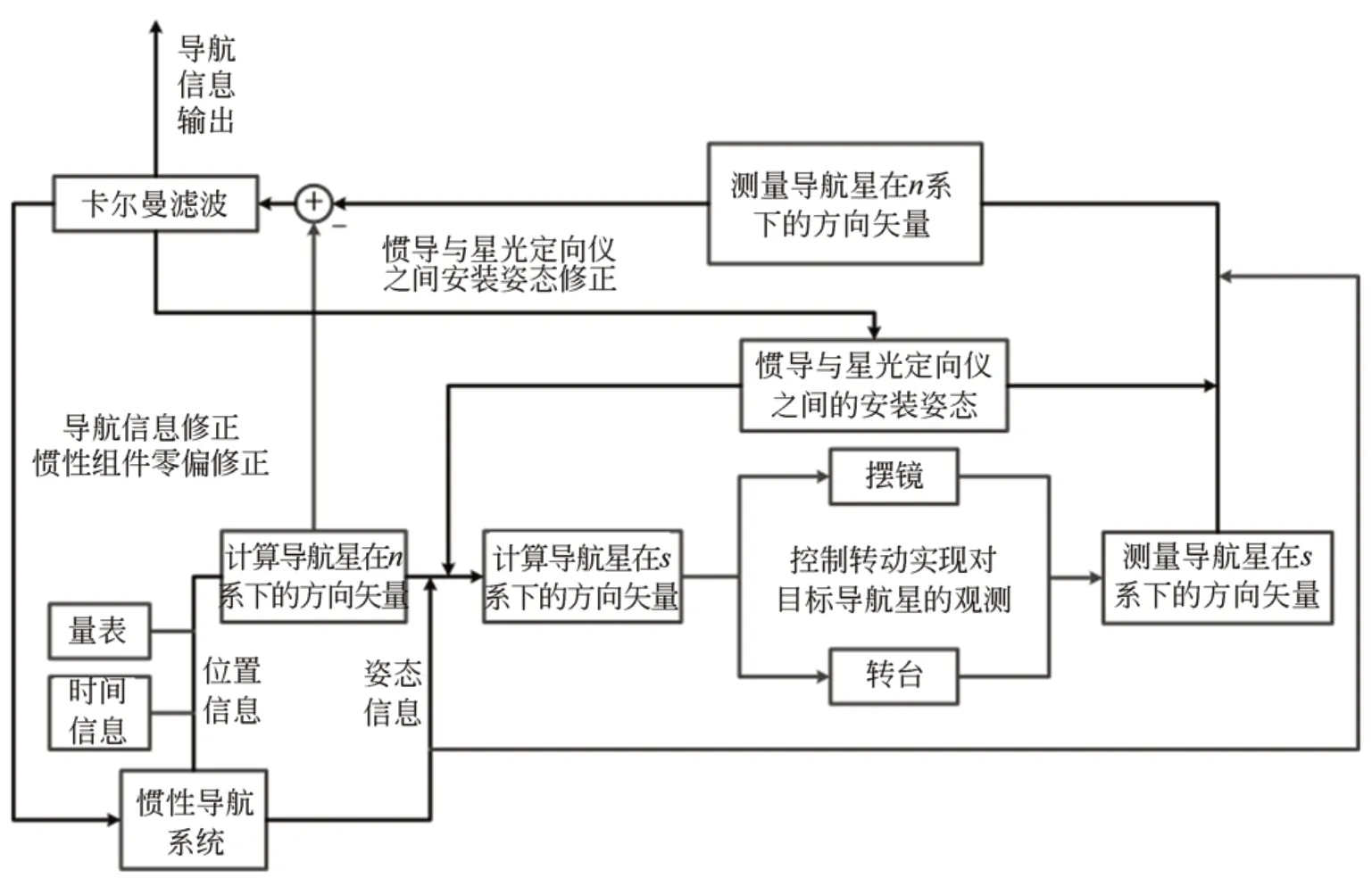
图2 基于单星测量的星光惯性组合导航系统的工作流程Fig.2 Work flow chart of starlight-inertial integrated navigation system based on single star vector

2.2 星光惯性组合导航算法

2.2.1 基本坐标系

为更好地说明组合导航算法，首先建立5 个基本的坐标系，分别为惯性坐标系（i）、地球坐标系（e）、导航坐标系（n）、惯导坐标系（b）和星光定向仪坐标系（s），并采用表示从a坐标系到b坐标系的转换矩阵。各坐标系的转换关系如图3 所示。具体公式如下：

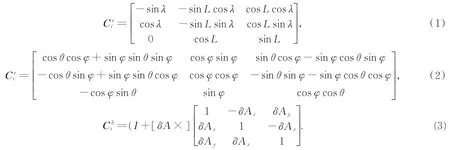
与天文历法有关，还需要考虑章动岁差等各种效应，在此不再赘述。

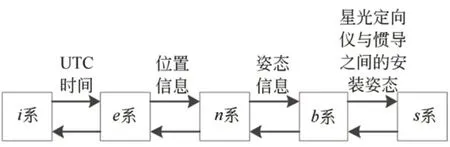
图3 星光组合导航各坐标系转换关系Fig.3 Relationship of coordinate systems in starlight-inertial integrated navigation

惯性坐标系（i）采用的是地心惯性系，其原地位于地球中心，z轴沿地球自转轴方向，x轴指向春分点，y轴与其他两轴组成右手坐标系。

地球坐标系（e）为地心地固坐标系，其原点位于地球中心，z轴指向北极，x轴指向0 度经线与赤道的交点，y轴与其他两轴组成右手坐标系。

导航坐标系（n）采用常用的东北天坐标系，原点位于载体位置，x，y，z3 轴分别指向正东，正北和垂直地球椭球面向上。

惯导坐标系（b），原点位于载体中心，x，y，z3轴分别指向惯导的右前上3 个方向。

星光定向仪坐标系（s）为星光定向仪的测量坐标系。理想情况下，星光定向仪与惯导之间的安装姿态为零，星光定向仪坐标系与载体坐标系重合。其中从i系到e系的转换需要将时间转换到儒略时，同时考虑地球自转的岁差章动极移等效应，具体可参见文献［18］，在此不进行赘述。

2.2.2 系统状态方程与测量方程

选取X =[φ δv δp ε ∇ δA]T作为状态 量 ， 其 中φ=[φEφNφU]T，δv=[δvEδvNδvU]T，δp=[δL δλ δh]T，分别为失准角、速度误差和位置误差；ε=[εx εy εz]T，∇=[∇x ∇y ∇z]T分别为陀螺和加速度传感器的零 偏 ；δA=[δAx δAy δAz]T，为 安 装 姿 态 误差角。

建立的系统状态方程与测量方程为：

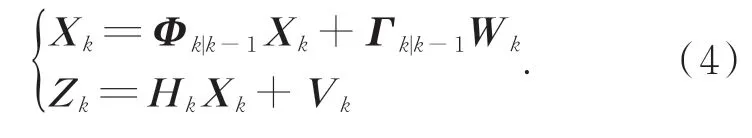
状态方程由式（5）中的惯导误差模型给出。

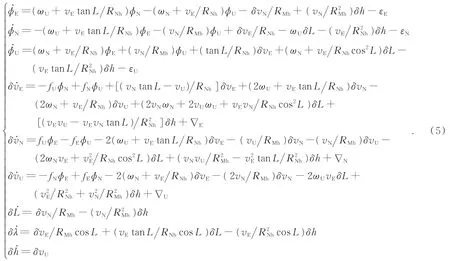
具体过程可参阅文献［19］，在此不进行赘述。

查阅星表可知观测时刻导航星在惯性坐标系下的方向矢量为Vi，由于惯导解算的位置存在误差，因此得到它在导航坐标系下的方位角αimu及高度角βimu应满足：

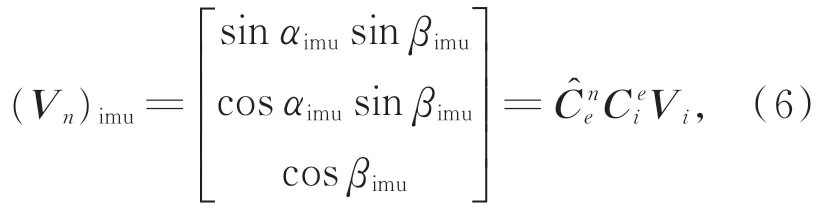
导航星在星光定向仪测量坐标系下的方向矢量Vs由星光定向仪给出。同时根据惯导姿态输出的姿态信息及星光定向仪与惯导之间的安装姿态也可得到导航星在导航坐标系下的方向矢量为：

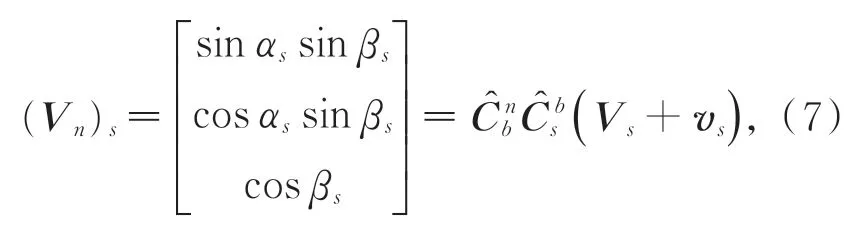
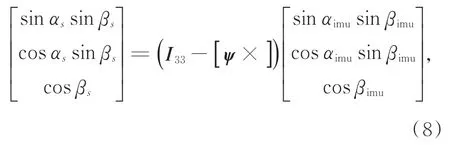
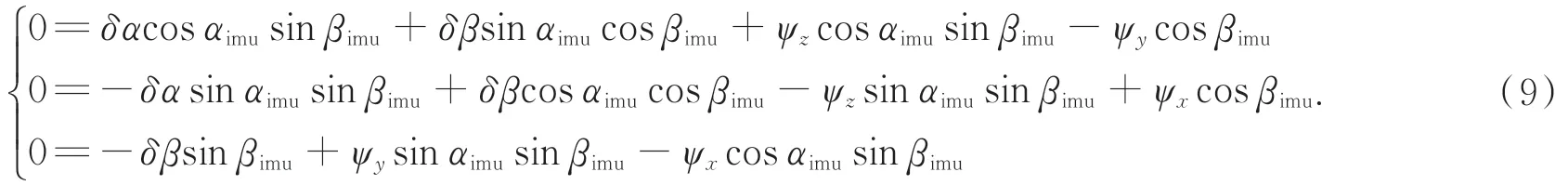
整理可得：

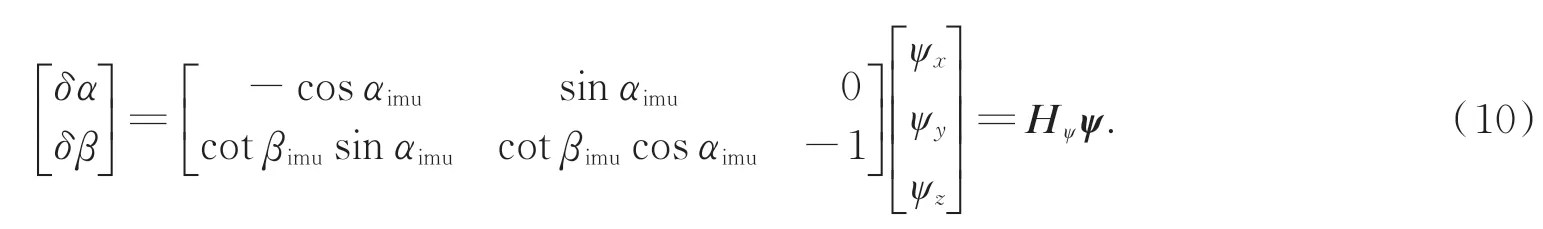
选取Zk=[δα δβ]T作为系统测量值，此时测量矩 阵其中：

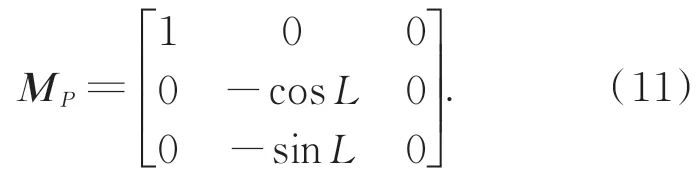
同时测量噪声Vk由星光定向仪的测量误差决定。

该算法引入星光定向仪与惯导之间的安装姿态误差角作为状态量。由于安装姿态在整个导航过程中可能随力热环境变化发生偏移，而这种漂移是不确定的，因此没有办法利用状态方程去描述；但安装姿态直接影响着惯导到星光定向仪之间的姿态转移矩阵，进而影响导航星在星光定向仪测量坐标系下的观测矢量，也直接体现在测量方程中。因此，可在组合导航的过程中对星光定向仪和惯导之间的安装误差进行实时的估计修正。

2.2.3 卡尔曼滤波修正

根据系统转台方程和测量方程即可利用卡尔曼滤波实现对状态量的估计和修正。卡尔曼滤波流程如图4 所示，分为预测和更新状态两步。

2.2.3.1 预 测

一步状态预测：

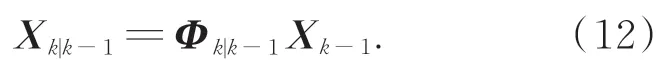
一步均方误差预测：

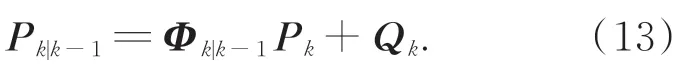
2.2.3.2 更新状态

滤波增益：

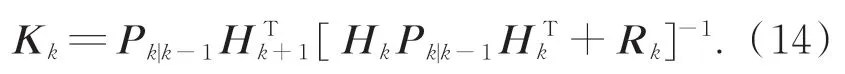
更新状态量：

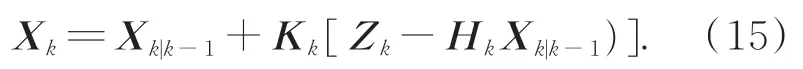
更新均方误差：

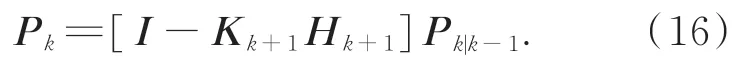
根据滤波得到的安装姿态误差δA对安装姿态估计值进行修正，即：

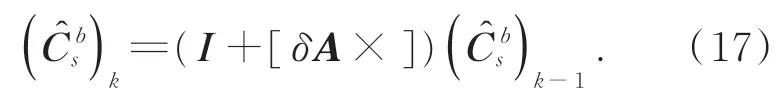
这样就可以在修正导航信息的同时对安装矩阵进行估计修正。

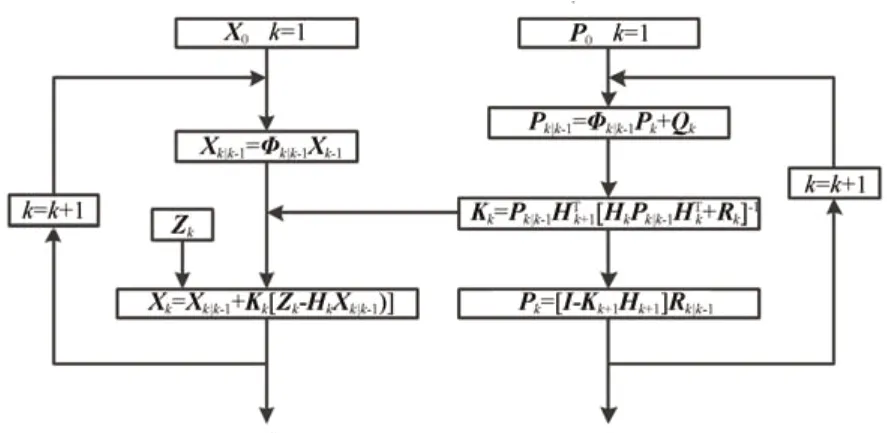
图4 卡尔曼滤波流程Fig.4 Flow chart of Kalman filtering

3 仿真实验

为进一步验证算法的有效性，进行了仿真实验分析。仿真实验为静态实验，将组合导航系统静止放置，利用惯导输出的姿态位置信息控制转台和摆镜旋转，实现对目标导航星的观测，利用观测导航星的方向矢量，采用第二部分介绍的方法对导航信息，惯性器件零偏，星光定向仪和惯导之间的安装姿态进行修正和补偿。

仿真实验中转台的初始姿态为（1.100 0°，-1.300 0°，26.700 0°），惯导安装在转台上，与转台的安装姿态为（0.100 0°，0.150 0°，-0.300 0°），星光定向仪安装在惯导上，安装姿态为（-0.080 0°，0.050 0°，-0.060 0°）。由此可得惯导的初始姿态为（1.193 2°，-1.155 8°，26.397 7°）。转台运动6 s 使星光定向仪指向下一颗导航星，然后停留2 s 对导航星进行观测。

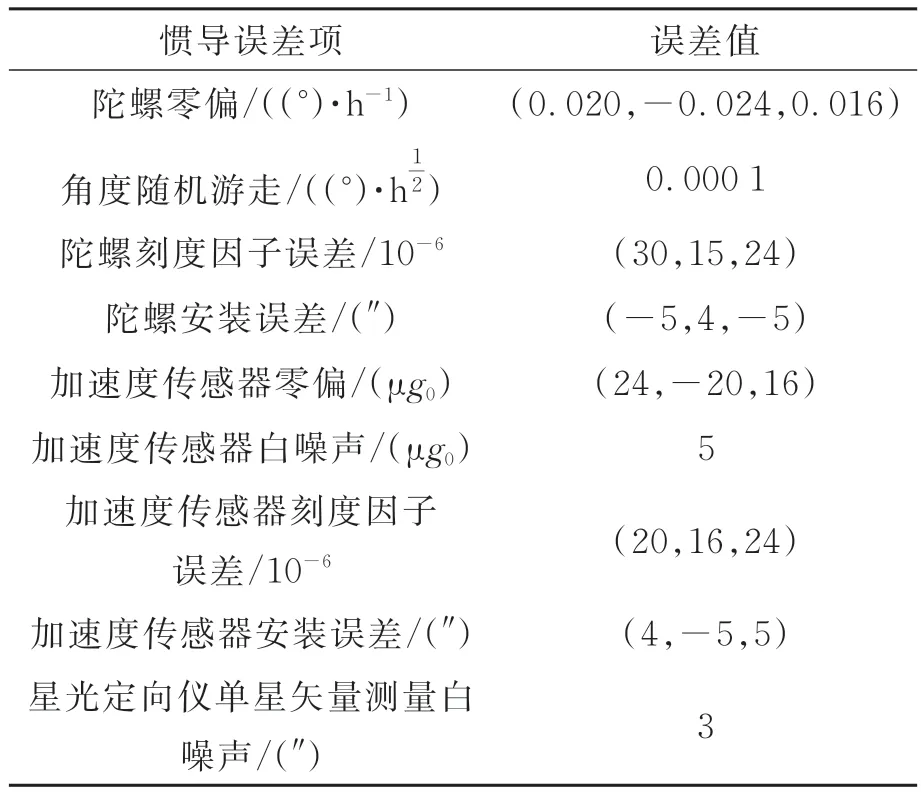
表1 星光惯性组合导航系统误差Tab.1 Errors of starlight-inertial integrated navigation system

星光惯性组合导航系统误差如表1 所示。采用解析法进行惯导的初始对准得到惯导的初始姿态为（1.193 0°，-1.158 5°，26. 371 2°），对准的姿态误差为（-0.000 1°，-0.002 7°，-0.026 6°），在此精度下可满足对目标导航星的观测需求。

静态导航1 h，取惯导与星光定向仪的安装姿态为0 作为滤波初值即=I，在导航过程中对安装姿态进行实时估计修正。估计得到安装姿态与实际安装姿态的误差如图5 所示，其中z轴为转台旋转轴，因此收敛速度较慢，最终估计得到惯导与星光定向仪之间的安装姿态为（-0.078 6°，0.049 0°，-0.061 0°），安装姿态的估计误差均优于4″。

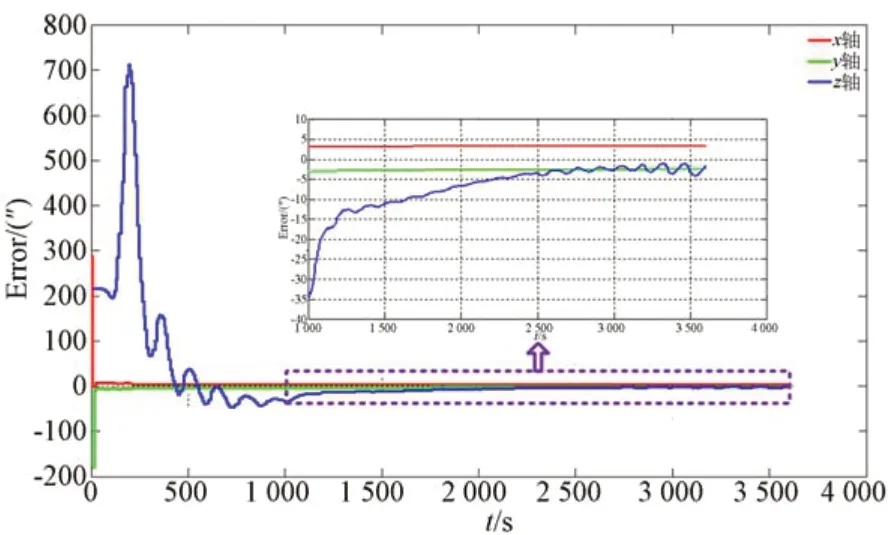
图5 星光定向仪与惯导之间的安装姿态误差Fig.5 Installation attitude errors between star sensor and inertial navigation

导航误差如图6 所示，由图6（a）可以看出俯仰滚转的姿态精度优于3″，航向姿态精度优于8″，图6（b）中最大位置误差为88.97 m。

若在导航过程中不对安装误差进行估计，采用实验室中的标定结果，则标定结果直接决定导航精度。不同标定残差对应的导航精度如表2 所示。采用文中算法在导航过程中对安装姿态进行实时标定，导航姿态精度与初始标定精度2″的导航结果相当，位置精度仅比完全标定好的导航精度低9.78 m，说明了文中算法的有效性。

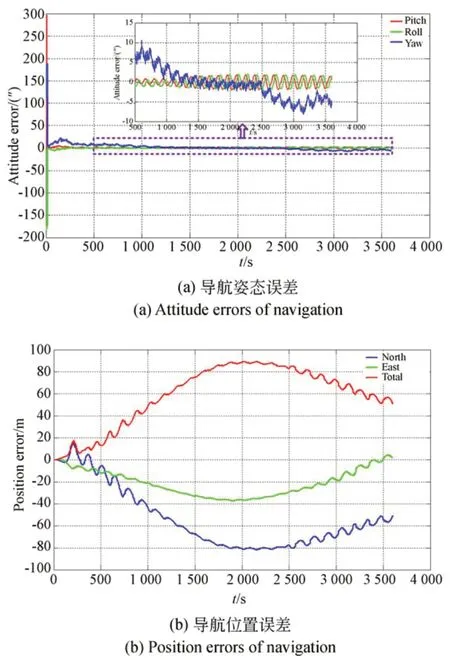
图6 组合导航误差Fig.6 Errors of integrated navigation

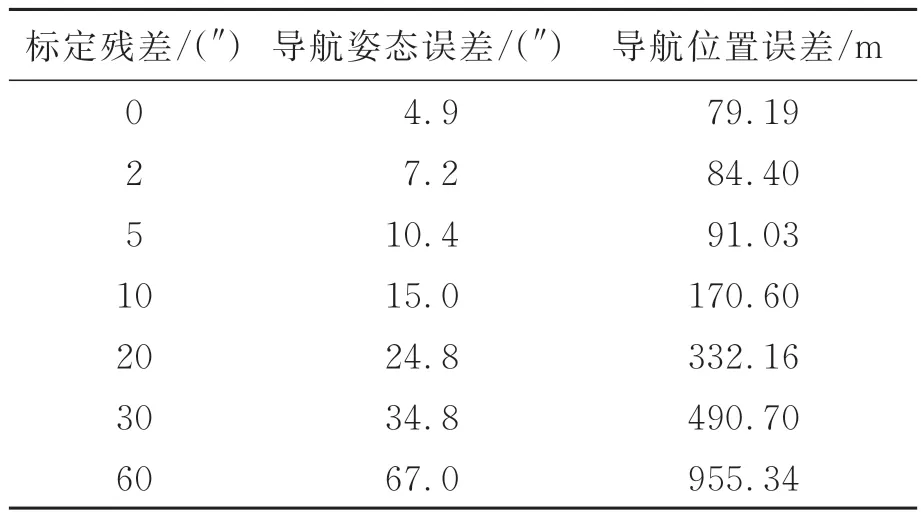
表2 不同标定残差对应的导航精度Tab.2 Navigation accuracy corresponding to different calibration errors

惯导和星光定向仪的测量精度直接决定了组合导航系统的精度。惯导误差包括陀螺和加速度传感器的零偏、白噪声、刻度因子误差以及安装姿态标定误差。其中，零偏是决定导航精度的最主要因素；星光定向仪的主要误差则是测量导航星矢量的白噪声。因此，本文分析了惯导陀螺及加速度传感器的零偏和星光定向仪的测量白噪声对导航精度的影响。星光定向仪的测量精度为3″，采用不同零偏的惯性器件，导航精度如图7 所示。不难看出，惯性器件零偏越小，导航精度也越高。采用零偏优于0.05（°）/h 的陀螺和零偏优于50 μg0的加速度传感器，可保证1 h 的导航精度优于150 m。

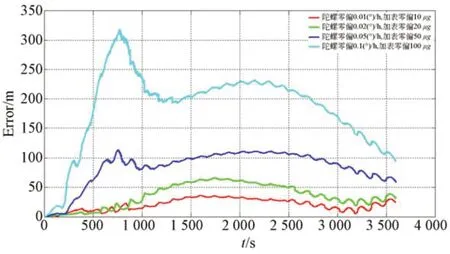
图7 惯性器件零偏对导航精度的影响Fig.7 Influence of inertial navigation components zero deviation on navigation accuracy

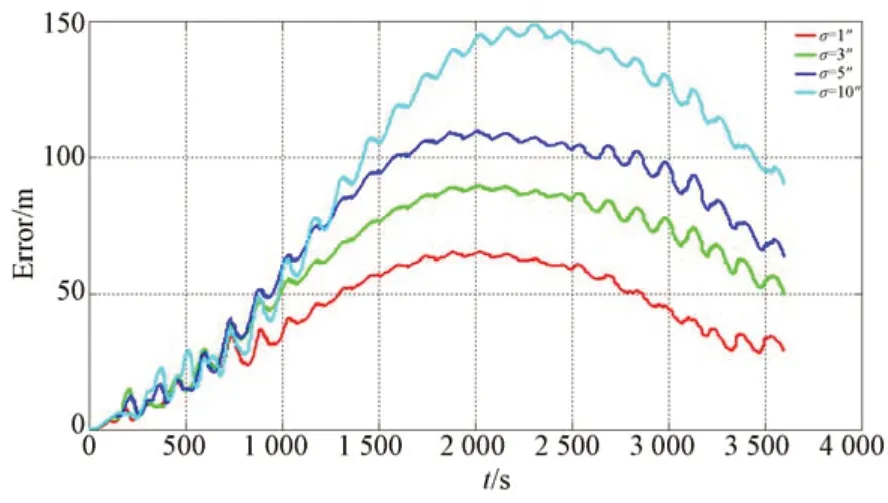
图8 星光定向仪误差对导航精度的影响Fig.8 Influence of star sensors error on navigation accuracy

陀螺零偏为0.02（°）/h，加速度传感器零偏为20 μg0，采用不同精度的星光定向仪，导航精度如图8 所示。不难看出，星光定向仪精度越高，导航精度也越高。采用测量精度优于10″的星光定向仪，可保证1 h 的导航精度优于150 m。

4 实 验

实验中惯导采用的角速度传感器是光纤陀螺，加速度传感器石英挠性加速度计，其零偏稳定性是通过Allen 方差统计得到的。3 支陀螺的零偏稳定性为 0.038 8，0.039 6，0.039 1（°）/h，3支加速度传感器的零偏稳定性分别为49.7，48.9，48.8 μg0。星光定向仪通过外场观星实验测量得到其单星测量精度为4.86″（1σ）。

实验采用的组合导航系统，在实验室已进行过星光定向仪与惯导之间的安装姿态标定，结果为（-110.6″，283.4″，-133.4″）。采用文中算法在导航的同时对安装姿态进行实时估计，修正结果如图9 所示。最终估计得到星光定向仪与惯导 之 间 的 安 装 姿 态 为 （-120.0″，278.7″，-146.3″）。可以看出，估计结果与实验室标定姿态相差（9.4″，4.7″，12.9″）。最终得到的导航误差如图10 所示。不难看出，若采用实验室标定结果直接进行导航，最大位置误差为188.42 m，而采用文中算法，在导航的同时对安装姿态进行实时估计修正，最大位置误差为102.90 m，导航位置精度提高45.39%。

图9 星光定向仪与惯导之间的安装姿态Fig.9 Installation attitudes between star sensor and inertial navigation

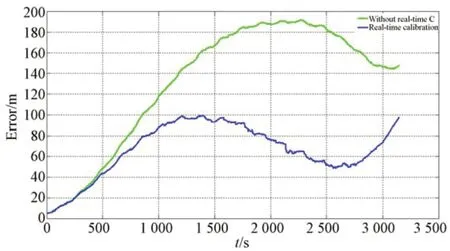
图10 导航实验结果Fig.10 Results of navigation test

5 结 论

本文提出一种基于单星测量的星光惯性组合导航方法。首先根据惯导输出的姿态和位置信息，控制转台和星光定向仪摆镜保证星光定向仪对目标导航星的观测，之后根据惯导的误差模型建立系统状态方程，根据星光定向仪测量的导航星方向矢量建立测量方程，利用卡尔曼滤波算法对惯导输出的姿态位置信息进行修正。通过仿真分析了不同安装姿态误差及不同惯导和星光定向仪误差对组合导航系统初始对准精度的影响，结果显示该算法具有较高的精度。搭建实验平台对组合导航算法进行验证，结果显示组合导航位置误差为102.90 m，相比直接采用实验室标定的安装姿态进行解算结果提高45.39%。该方法引入星光定向仪与惯导安装误差作为系统状态量，在修正导航信息的同时对星光定向仪与惯导之间的安装误差进行估计，因此无须在实验室进行标定，具有较高的工程应用价值。