基于蒙特卡罗法的星载太阳辐照度光谱仪对日指向误差分析

郭 旭，胡春晖，颜昌翔，郭永飞，马泽龙，胡庆龙

（1. 中国科学院长春光学精密机械与物理研究所，长春吉林130033；2. 中国科学院大学，北京 100049）

1 引 言

太阳辐照度光谱仪作为太阳光谱监测的主要光学载荷，为气象领域提供了大量的数据支撑。光谱仪载荷主要包括不同谱段的谱仪设备、用于对日指向跟踪的导行镜、以及用于提供指向功能的二维转台等部件。目前，国内外对于太阳辐照度光谱仪的研究均取得了一定的进展，研究内容主要围绕光谱仪载荷本身的设计以及光谱仪对日指向精度等方面。

在光谱仪载荷设计方面，李占峰［1］等研究了多通道光谱仪中光谱仪输出波长与光谱仪内部调节丝杠的位移非线性问题，并给出了相应的理论公式。曹佃生［2］等根据太阳光谱仪中对于波长重复性的指标要求，对光谱仪内部的波长扫描机构进行了设计，并对扫描机构的精度进行了分析。李寒霜［3］研究了太阳辐照度光谱仪中紫外-真空紫外波段的光谱定标以及辐射定标的问题，并构建了一套可以实现150～300 nm 波段测量的定标系统。孙德贝［4］等根据光的叠加原理研制了一台太阳光谱仪探测系统线性度的测试装置，该装置的工作波段为200～2 400 nm，可模拟多谱段的太阳光谱特性。李福田［5］等针对高精度空间太阳光谱仪的辐射定标问题，研制了一种采用数字微镜器件的光谱辐亮度标准光源，为太阳光谱仪的辐射定标提供硬件基准。李占峰［6］等介绍了一种由卫星平台当前广播事件和轨道瞬根来推导预报短时太阳角度的方法，该方法预报的最大角度误差为0.5°，预热时间的最大偏差为20″。孙立微［7］针对太阳高光谱的辐射定标问题，研制了由激光二极管配合钨灯的定标光源，为太阳辐照度光谱仪的辐射定标提供了良好的光源基准。窦晨浩［8］针对太阳光谱仪在轨工作过程中获取到的偏振测量数据、修正数据以及大气探测数据等，采用定量化分析法进行了分析与研究。

在光谱仪对日指向精度方面，其研究主要为二维指向机构、导行镜及光谱仪在各环节中的加工、装调误差最终合成后对于太阳指向性能的影响。王金元［9］等分析了一种小口径的相控阵天线的指向误差，并提出了降低各项误差的方法，可有效提高指向精度。胡晓炜［10］等以地平式望远镜为模型，对其指向误差进行建模及分析，并介绍了指向误差数据的获取方法。通过修正系数可有效降低设备的指向误差，提升指向精度。康跃然［11］等分析了三轴转台姿态变化时各误差分量对于最终的系统指向误差的影响，同时通过仿真获取各个误差分量的变化规律，为后续的误差分配及补偿提供了理论依据。吴伟平［12］等建立了在轨视轴临边指向的误差补偿方法，消除了探测仪器由于外界客观因素所导致的指向误差。该方法可以将指向误差控制在±3.08″的范围内。

为实现光谱仪对日指向，将太阳引入导行镜视场，需要建立太阳矢量、卫星姿态和安装误差等因素与转台转角的数学关系。本文首先采用坐标变换法建立光谱仪载荷系统的坐标系及相应的变换矩阵的数学模型；然后通过蒙特卡罗法分析载荷整机的各项误差，仿真得出对日指向误差；最后开展对日指向模拟实验，验证了理论分析及仿真结果的准确性及有效性。

2 光谱仪系统模型

2.1 系统组成

根据太阳辐照度光谱仪工作的轨道参数，一年内太阳光在轨道面的入射角在约47°的范围内变化，远大于光谱仪的有效视场。根据光谱仪的工作特点和任务需求，需设计二维转动机构，对卫星偏航和俯仰方向的轨道运动进行补偿。

星载太阳辐照度光谱仪载荷整机是由两台太阳某谱段的光谱仪、一台导行镜、以及搭载上述光学有效载荷的二维转台组成。二维转台作为该载荷的核心，主要由基座、方位轴系（U 形架）和俯仰轴系（O 形架）等部组件构成。方位U形架为外框架，安装在转台基座上，俯仰O 形架为内框架，安装在U 形架上，导行镜和光谱仪安装在O 形架上。光谱仪二维转台的三维模型如图1 所示。

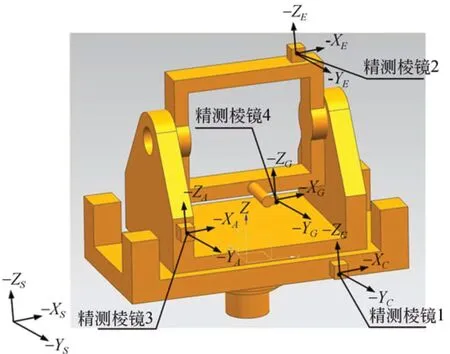
图1 二维转台模型Fig.1 Model of two-dimensional turntable

2.2 工作原理

载荷在轨工作时，首先调整二维转台方位、俯仰角位置实现对日指向功能，使太阳进入导行镜有效视场；然后依据导行镜偏移量实时调整两轴角位置实现对日跟踪；只有当跟踪误差低于一定范围时，即太阳小角度偏离谱仪视场中心时，两台光谱仪方能获取有效的光谱数据。因此，转台对日指向是载荷能够有效工作的前提。

由于卫星姿态的实时调整、载荷整机相对卫星平台存在安装误差以及载荷内部组件间存在安装误差等因素，需要实时计算二维转台的工作角度。具体地，根据卫星平台的广播数据，获取当前轨道坐标系下的太阳矢量和卫星姿态角测量值，并对安装误差进行修正，进而计算出转台方位轴和俯仰轴的转动角度，最终保证太阳位于导行镜的有效视场内，并尽量靠近视场中心。

3 对日指向数学模型

3.1 系统坐标系建立

载荷整机的坐标系建立方式由它在卫星平台上的安装方式决定。对于卫星平台，X方向为飞行方向，Z方向指向地心，Y方向由右手法则确定。载荷在卫星平台上的安装方式如图2 所示。

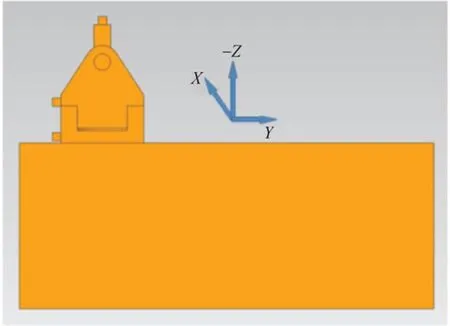
图2 转台安装示意图Fig.2 Assembly of turntable

首先建立轨道坐标系O（OO-XOYOZO），坐标原点OO位于卫星质心，ZO指向地心，XO轴位于轨道平面内并指向卫星飞行方向，YO通过右手坐标系确定。卫星坐标系S（OS-XSYSZS），坐标原点OS与OO重合，卫星无姿态运动时，O系与S系重合，卫星的三轴姿态角φ，θ，ψ即指S系在O系内的三轴姿态描述。确定卫星坐标系后，如图1 所示，在转台基座上的精测棱镜1 上建立基座坐标系C（OC-XCYCZC），若忽略精测棱镜的安装误差、角度加工误差，XC，YC，ZC分别与精测棱镜 1 的 3 个表面垂直，正方向与卫星坐标系相同，后续棱镜坐标系的定义与之相同，不再赘述。在方位轴U 形架的精测棱镜3 上建立方位轴坐标系A（OAXAYAZA），在俯仰轴 O 形架的精测棱镜 2 上建立俯仰轴坐标系E（OE-XEYEZE），在忽略 U 形架在载荷基座的安装误差时，方位零位时A系与C系三轴平行。类似地，若忽略O 形架在U 形架的安装误差时，俯仰零位时E系与A系三轴平行。在导行镜精测棱镜4 上建立导行镜坐标系G（OG-XGYGZG），-Y方向代表视轴。

3.2 坐标变换矩阵推导

已知各个组件的局部坐标系后，基于坐标变换的原理，太阳矢量从轨道坐标系下的矢量表达至导行镜坐标系下的矢量表达式为：

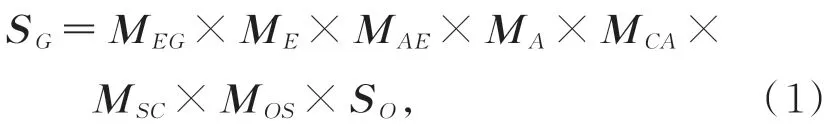
其中：SG为导行镜坐标系下的太阳矢量，规定其坐标为［0 -1 0］T；SO为轨道坐标系下的太阳矢量，假设其坐标为［XsunYsunZsun］T，该太阳矢量数据由平台广播数据提供；MOS是由卫星相对于轨道姿态变化引起的变换矩阵；MSC为卫星坐标系至转台基座坐标系的变换矩阵，通过标定精测棱镜1 的姿态可以获得；MCA为基座坐标系至方位轴系坐标系的变换矩阵，通过标定精测棱镜1 和3 的姿态可以获得；MAE为方位轴系坐标系至俯仰坐标系的变换矩阵，通过标定精测棱镜2 和3 的姿态可以获得；MEG为俯仰轴坐标系至导行镜坐标系的变换矩阵，通过标定精测棱镜2 和4的姿态可以获得；MA，ME分别为方位轴系、俯仰轴系转动前后局部坐标系的变换矩阵。

在明确上述变换环节中各个矩阵的意义后，对各变换矩阵的形式进行推导［13-15］。假设卫星相对轨道坐标系的滚动角（绕XO轴）、俯仰角（绕YO轴）和偏航角（绕ZO轴）分别为φ，θ，ψ，则MOS为：

MSC可根据卫星平台精测棱镜及转台精测棱镜1 的经纬仪标定结果给出，其值如下：

同理，MCA，MAE及MEG也可根据经纬仪对相关精测棱镜的标定结果给出，模型中4 个精测棱镜的标定结果详见表1。其中，棱镜i-i的值代表自准值；棱镜i-j的值代表互瞄值，i，j的取值均为1～4。

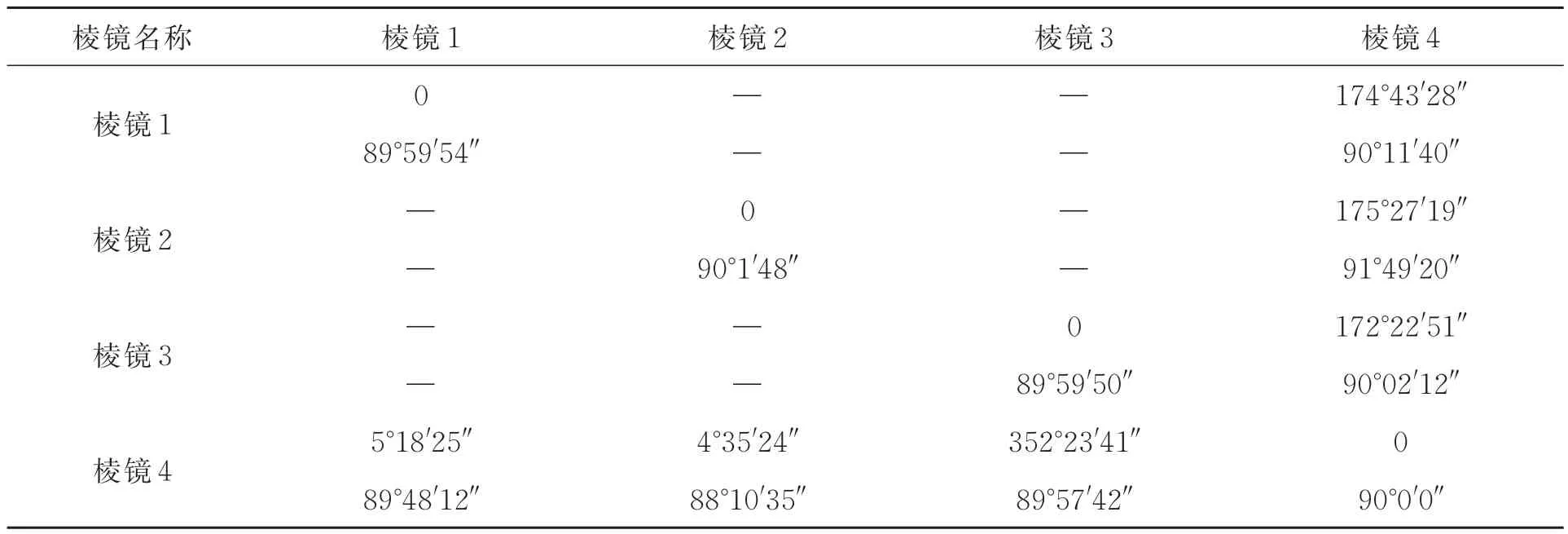
表1 精测棱镜的标定结果Tab.1 Calibration results of prisms for precise measurement

根据表1 的数据求得MCA，MAE及MEG的表达式，分别为：

MA为方位轴转动前后的变换矩阵，其值为：

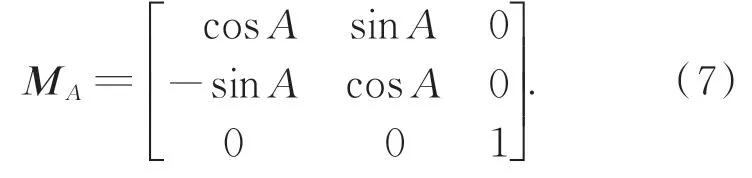
同理，ME的形式为：

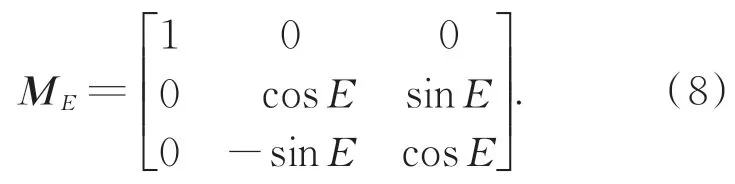
3.3 运动学反解结果

当忽略卫星姿态角度、载荷整机在卫星平台上的安装误差以及方位轴系、俯仰轴系、导行镜等各组件在转台上的安装误差时，各个坐标系的坐标轴平行，变换矩阵简化为单位阵。则式（1）化简为：

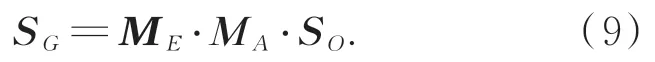
将式（7）和式（8）代入式（9）后，可解算出转台方位轴及俯仰轴的转动角度为：

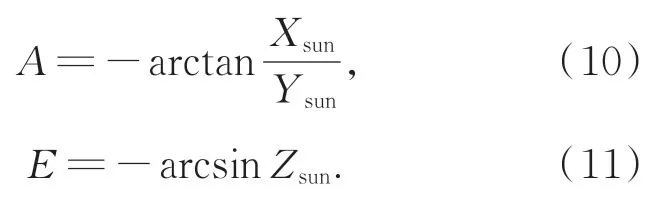
上述求解出的转台运动角度为忽略平台姿态调整和安装误差等因素得到的结果，即理论真值。但实际工程中会存在多个环节的误差，为兼顾工程中实际误差的必然性以及解析计算的便利性，鉴于式（5）俯仰轴系与方位轴系的安装误差相对较小，考虑软件的在轨计算效率，将它忽略不计。其余误差变换矩阵纳入计算环节，通过坐标变换矩阵反解出转台方位轴及俯仰轴的工作转角。

首先，计算太阳矢量在转台基座坐标系下的矢量表达，记为：

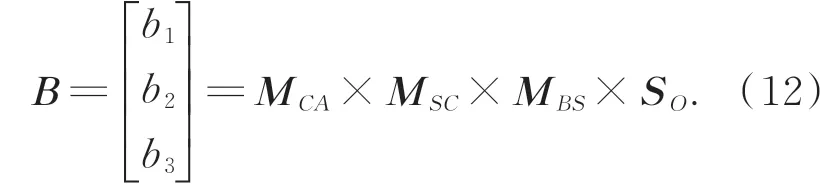
其次，得到太阳矢量在俯仰轴坐标系下的矢量表达，记为：

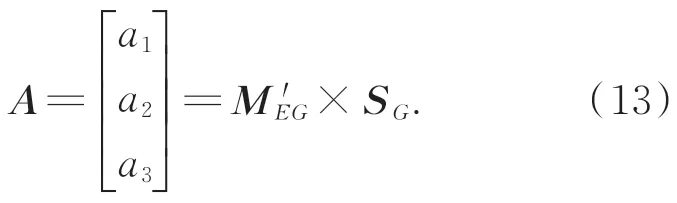
将上述表达式代入式（1），即：

通过式（14）可以反解出方位轴及俯仰轴的转动角度，即：

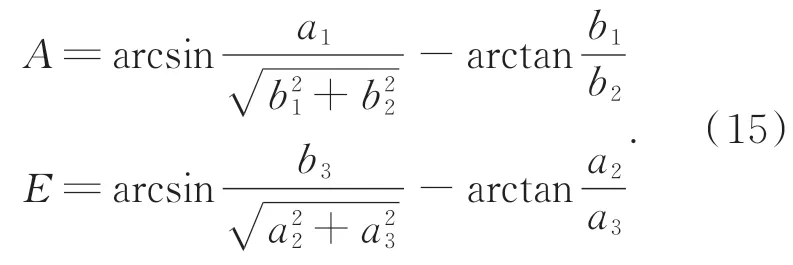
4 指向误差分析

由第三部分的计算结果，可以得到任一组太阳矢量及相应安装误差下的转台工作转角。由于各项误差均存在一定的分布区间，需要保证在统计学角度的极端情况下，太阳矢量依然位于导行镜视场中心。

4.1 误差仿真

误差仿真流程如下：

（1）指定某种工况并设定仿真模型的参数，将上述参数作为仿真场景的真值，参数包括太阳矢量、卫星姿态和安装误差等；

（2）根据第一步设定的仿真理论参数，计算转台方位、俯仰调整角的真值；

（3）根据平台姿态和太阳矢量的数据误差，以及转台内部各部组件的安装测量误差，将第一步的无误差数据误差化，得到实际的转台方位、俯仰目标调整角；

（4）根据第三步的计算结果控制转台转动，转台定位误差为编码器的测量误差，可得实际控制输出的方位、俯仰调整角，将实际值与真值比较，得出转台对日指向的最终实际误差。

4.2 蒙特卡罗分析

根据前文内容可知，系统工作过程中有多个环节存在误差，从误差性质上可分为系统误差和随机误差，从误差种类上分为运动误差、安装误差、加工误差及测量误差等。分析多个误差源对最终结果的影响，需要引入基于蒙特卡罗法的误差模型。

蒙特卡罗法是基于变量的统计学特性，使用随机变量代替常量，同时保证随机变量满足一定的概率分布，使最终的计算结果更加逼近使用常量所得到的结果［16］。鉴于本系统中误差项较多，在后续的计算中将每一项误差均视为一个随机变量，并且它满足正态分布。从分布区间中取出若干组数据代入公式进行计算，从而得到最终结果的分布情况，即可确认载荷的整体误差是否满足工况需求。

根据二维转台内各个精测棱镜的测量结果，以及外部提供的设计输入，可以获得下列仿真参数：

（1）太 阳 矢 量SO=[XsunYsunZsun]=[0.085 -0.981 0.176]T；

（2） 卫 星 姿 态 ［φ θ ψ］= [0.060 3-0.051 8 0.028 3］；

（3）载荷基座相对于平台的安装误差［φC θC ψC]=［0.013 1o0.012 2o0.016 1o］；

（4）转台轴系相对于基座的安装误差[φAE θAE ψAE]=[ 0.031o-0.073o0.014o]；

（5）导行镜相对于转台轴系的安装误差[φG θG ψG]=[ -0.03o0.083o-0.045o]。

在MatLab 中建立变换矩阵的数学模型，并代入上述仿真参数，可以求得当方位轴转角A0=3.951°，俯仰轴转角E0=-13.316 9°时，太阳处于导行镜视场中心。

上述计算是基于各项误差为常数，下面引入基于蒙特卡罗的误差模型。采用正态分布函数，并适当选取期望及标准差。其中，太阳矢量误差和姿态测量误差通过分析卫星运动的仿真数据和在轨实测数据预估；各项安装误差修正后为经纬仪测量误差，依据工程经验预估；时延误差针对在轨软件的具体实现进行估算；转台定位误差取决于编码器的测量误差。各项误差的估计值详见表2。

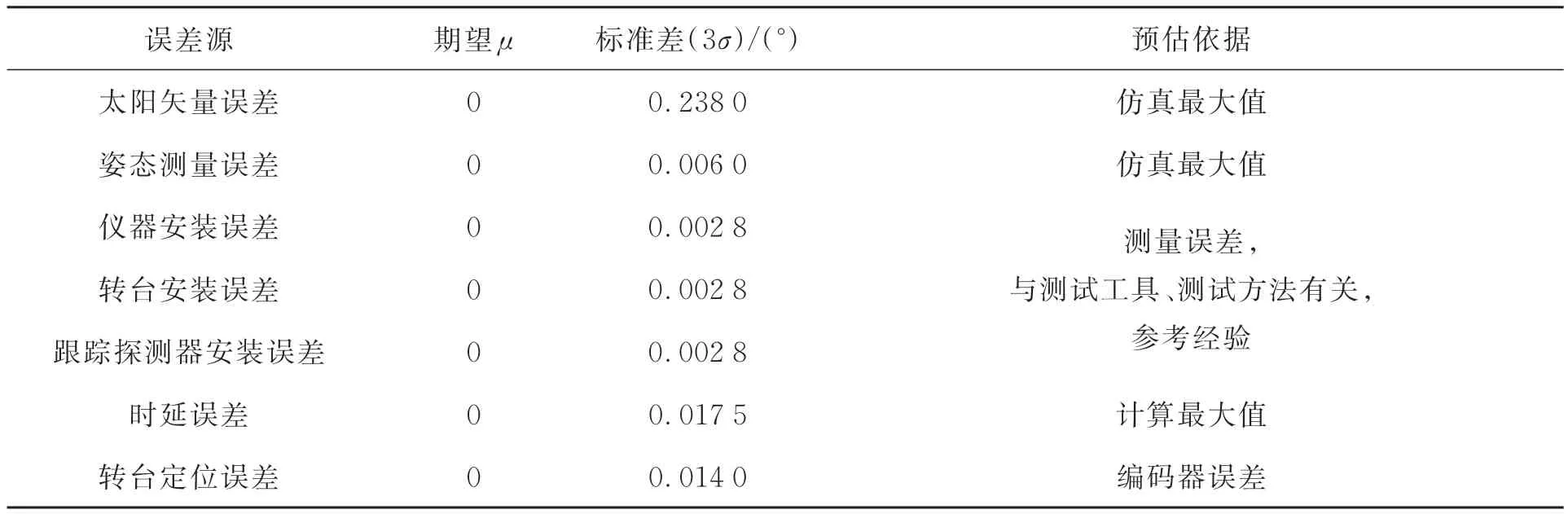
表2 对日指向各项误差预估Tab.2 Estimation of systematic sun pointing errors

4.3 结果与讨论

根据表2 中的各项误差值，在各个误差维度下分别生成10 000 组随机数进行仿真。经过仿真，转台方位转角及俯仰转角数据的直方图如图3 所示。从图3 可以看出，转台转角的仿真值大部分分布在理论真值附近，在方位、俯仰两个维度上呈正态分布规律。转台对日指向误差的仿真结果如图4 所示。

根据指向误差的仿真结果，方位轴的最大误差为 0.338 7°，俯仰轴的最大误差为 0.294 5°。从图4 可以看出，指向误差分布在1°的圆形视场中，且全部分布在0.35°以内，意味着通过调整转台的方位角和俯仰角，能够保证太阳进入导行镜的有效视场，仿真结果满足指向任务需求。

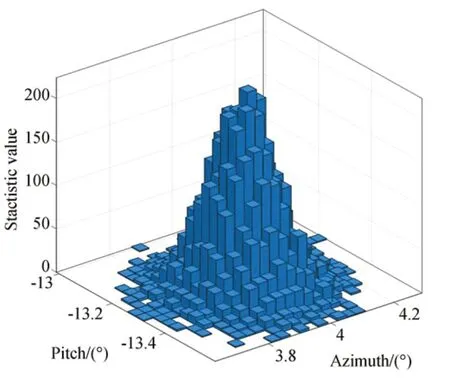
图3 转台转角直方图Fig.3 Histogram of rotation angles of turntable

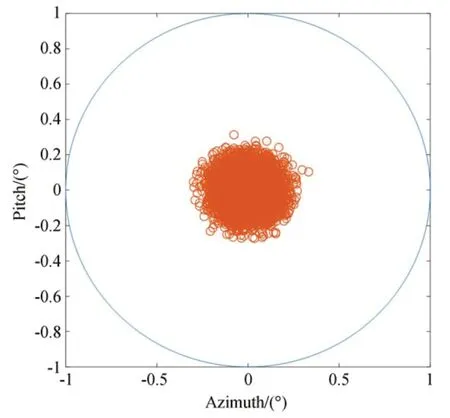
图4 指向误差的仿真结果Fig.4 Simulation result of pointing errors

5 模拟实验

5.1 实验环境

为了验证上述理论分析及仿真结果的准确性及有效性，在实验室环境下，搭建光谱仪对日指向模拟实验，用于模拟转台对日指向过程。

实验环境如下：在导行镜前端放置一台平行光管，并在焦面处放置一个强光光源，以模拟太阳光，并且该光源在导行镜视场内的光斑大小与太阳近似；将二维转台置于高精度六自由度平台上，该平台的转动范围大于转台转动角范围，控制精度优于卫星平台的在轨姿态控制精度，能够模拟卫星姿态以及卫星飞行时太阳位置的变化。

初始状态为光源光线沿+Y轴方向射入导行镜视场。实验现场示意图如图5 所示。

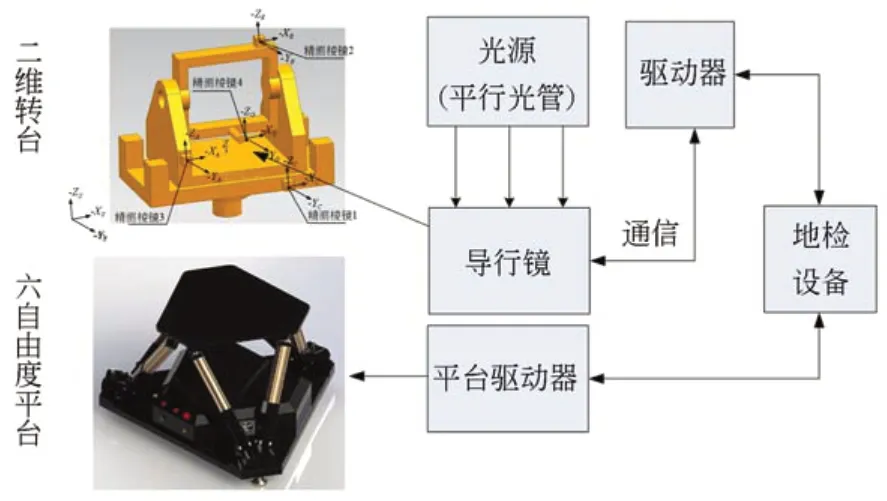
图5 对日指向实验现场示意图Fig.5 Schematic diagram of Sun pointing test

5.2 指向实验

根据光谱仪载荷在轨的实际工作状态，选取有代表性的工况进行模拟实验。实验分两步：第一步是选取4 种典型工况，令转台方位轴和俯仰轴自转台零位向不同方向转动，验证对日指向的数学模型；第二步是选取典型工作轨道，令转台在一轨工作中长时间保持对日指向，测量指向误差低于1°。具体实验流程如下：

（1）测量光谱仪转台基座在六自由度平台上的安装误差，记为［φcθcψc］；

（2）选取 4 组太阳矢量［XsunYsunZsun］、卫星姿态［φ θ ψ］，将参试设备安装误差的测量结果、选取的太阳矢量和平台姿态数据带入对日指向数学模型中，反解转台方位和俯仰目标角；

（3）根据选取的数据分别驱动六自由度平台和二维转台转动；

（4）记录导行镜测得的角偏移量，该参数为指向误差与导行镜测量误差的合成结果，其中导行镜的测量误差为 3″（3σ）；

（5）选取春分轨道的太阳矢量和卫星姿态数据，重复步骤（1）～（4），对转台长时间工作的指向误差进行验证和分析。

5.3 结果与讨论

将实验环境搭建完成后，首先测量光谱仪载荷基座相对于平台的安装误差为：

[φcθcψc]=[0.011° 0.005° 0.007°].

然后依次测量转台方位轴和俯仰轴正、反转4 种工况下的指向精度。实验参数（太阳矢量、卫星姿态参数和转台转角）和实验结果详见表3。

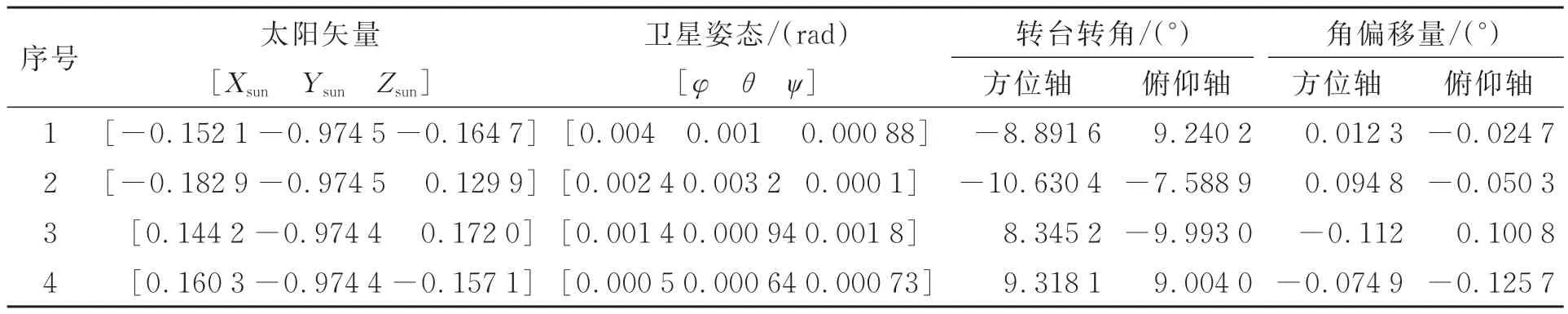
表3 对日指向实验参数及结果Tab.3 Parameters and results of sun pointing test

由实验结果中测得的导行镜偏移量数据可知，两轴最大指向误差为 0.125 7°，低于 1°，因此采用本文提出的对日指向数学模型，转台能够将太阳引入导行镜的有效视场。

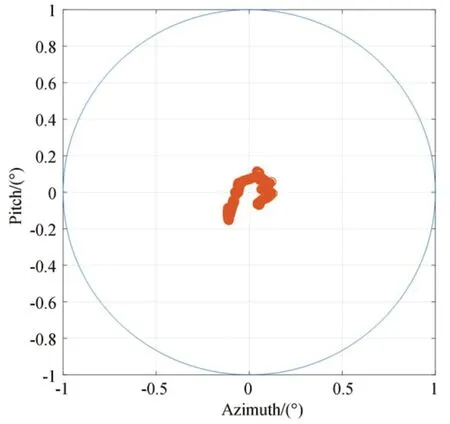
图6 对日指向误差测试结果Fig.6 Test results of sun pointing errors

重复上述实验过程，选取一轨春分轨道的太阳矢量和卫星姿态数据，令六自由度平台依据当前数据运动，实时解算转台转角驱动转台转动，测量600 组导行镜偏移量，指向误差如图6所示。由图可知，方位轴的最大指向误差为0.126 5°，俯仰轴的最大指向误差为 0.154 2°，实验测得指向误差处于仿真分析的误差范围内。实验中六自由度平台未模拟太阳矢量的误差数据，因此实验测得的误差最大值稍低于仿真分析结果。

对日指向模拟实验结果一方面验证了本文提出的转台对日指向数学模型的准确性；另一方面，测得的指向误差验证了误差仿真分析结果，说明转台对日指向误差在导行镜的有效视场内，能够满足载荷在轨工作的要求。

6 结 论

光谱仪的对日高精度指向对卫星在轨工作至关重要。本文采用坐标变换矩阵法，对太阳辐照度光谱仪的系统坐标系及矩阵变换关系进行了分析并建立了相应的数学模型，得到了二维转台工作转角的解析解；利用基于蒙特卡罗法的误差模型分析光谱仪载荷系统的整体误差，并进行了对日指向误差仿真实验，实验结果表明指向误差优于0.35°；最后，通过转台对日指向模拟实验对所建立的数学模型和误差仿真分析结果进行了验证，测得不同工况下转台的指向误差低于0.16°。通过转台的高精度指向，太阳能够进入导行镜视场内，满足光谱仪系统的设计指标要求及在轨工作要求。