高温高压和高速工况下SCO2动压密封端面的热弹变形研究*
2021-04-22陈坤毅马润梅廖浩然施任杰程天馥李双喜
陈坤毅,马润梅,廖浩然,施任杰,程天馥,李双喜
(北京化工大学 机电工程学院,北京 100029)
0 引 言
近年来,SCO2因具有的高密度特性,能实现高效转化的能量循环,被广泛应用于各个领域。以SCO2为工质的能量转换系统被认为是最具应用前景的系统之一[1,2]。SCO2布雷顿循环效率可达52%[3],能源的高效转化主要依赖热力循环系统,而热力循环系统存在的轴端密封泄漏问题,是影响其能量转换效率的关键因素。
与普通机械密封相比,动压密封端面无磨损,也不需要润滑油系统,适用于高压、高温、高转速工况,具有泄漏量低、驱动功率小、稳定性好等优点,目前已在石油化工透平机械中得到了广泛应用[4]。动压密封的动静环需要在光滑,且接近平行的表面才能正常工作。在理想情况下,密封的动环和静环之间的间隙是恒定且平行的,但是由于循环装置透平机轴端密封工况苛刻,在使用过程中,其表面会因热载荷、压力载荷、离心效应或其他条件而产生变形[5]。这些微米级的小变形会造成端面接触、过度张开或气膜不稳定性等现象,特别是在高温、高压、高转速的条件下,变形更为显著,严重影响其安全性能和使用寿命[6]。
针对以上这些问题,王延忠等[7]分析了热固耦合下动环的热变形及动环材料属性对密封特性的影响,指出材料的导热系数、泊松比和热膨胀系数与动环的热变形成拟线性关系;丁雪兴[8]对柱面螺旋槽干气密封进行了流固分析,并得出结论,即压力是浮环变形的主导因素。GALENNE E[9]和BRUNETIéRE N[10]利用影响系数法计算了密封环的热弹变形,所得结果较为理想;李娜[11]分析了T型槽干气密封的温度场及热变形,提出了密封环优化方法和热变形控制措施;李香等[12]利用ANSYS软件计算了高压水泵密封环的耦合变形,他指出耦合变形不是简单地将力变形和热变形进行叠加,在高压状态下,热变形占据主要地位;FRÖLICH D[13]综合考虑温度、摩擦因素的影响,模拟了弹性体密封环的接触行为,并将仿真结果与实验值进行了对比;王冲[14]针对高参数石油化工设备气膜密封变形进行了求解,并从密封环约束方面提出了减小端面变形措施;袁艳艳[15]研究了高温热油泵密封端面力热耦合变形,并从理论方面提出了减小变形的方法。
在超临界二氧化碳涡轮机械运行过程中,轴端密封在所处的高温、高压和高转速工况下,容易因热弹效应导致密封端面变形。为避免过大的密封端面变形导致密封失效,就需要分析热弹作用下密封端面的变形规律与其主要影响因素。但是,在现有针对密封端面变形的研究中,密封介质多为普通介质,对于SCO2变物性介质和高工况参数下的端面变形的研究则较少。
本文以超临界二氧化碳螺旋槽动压密封为研究对象,利用有限元软件建立超临界二氧化碳密封环和流体膜数值分析模型,调用REFPROP数据库二氧化碳真实物性数据,并考虑粘性耗散的情况,对密封进行热流固耦合分析,求解密封端面的热弹变形;同时,研究操作参数对密封端面热弹变形的影响规律,为高温、高压和高速工况下超临界流体的机械密封设计提供理论依据。
1 计算模型
1.1 几何模型
超临界二氧化碳动压密封结构原理如图1所示。

图1 超临界二氧化碳动压密封结构原理图1-静环座;2-轴套;3-弹簧;4-推环;5-静环;6-卡环;7-动环;8-垫圈;9-O型圈
在图1(a)中,密封环外侧为高压SCO2流体,内侧为大气压。其基本工作原理是:在密封环的高速旋转下,外侧SCO2流体在螺旋槽的泵入作用和流体压差作用下进入端面,形成微米级厚度的流体膜,流体膜依靠螺旋槽产生动压效应,使动静环端面推开,处于非接触状态。
其具体的流体膜结构参数如表1所示。

表1 流体膜结构参数
密封环结构参数如表2所示。

表2 密封环结构参数
密封环材料属性如表3所示。

表3 密封环材料属性
其典型工况参数为:密封进口压力Pi=9 MPa,出口压力Po=0.1 MPa,介质温度Ti=4 3 0 K,转速n=5 0 000 r·min-1。
耦合数值分析模型如图2所示。

图2 耦合数值分析模型
1.2 网格划分
由于密封环及流体膜均具有周期对称性,此处笔者选取全周期的1/12进行建模求解。
笔者建立的SCO2密封环和流体膜几何模型与网格划分结果,如图3所示。
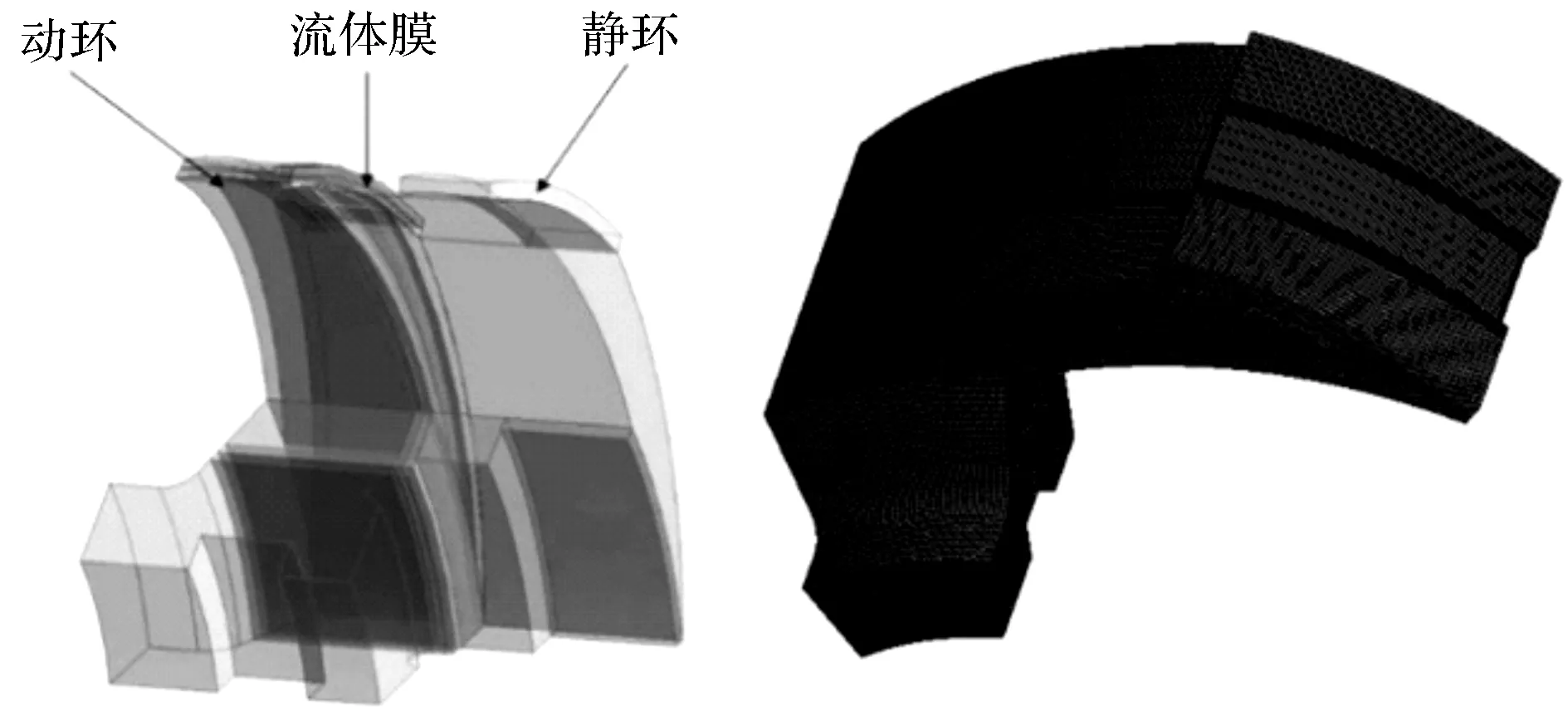
图3 几何模型与网格划分结果
整个计算模型分为流体和固体两部分,采用Sweep六面体网格划分方法,在厚度方向控制网格单元数目,在端面控制网格尺寸大小。经网格无关性验证,流体膜的网格数为48 874个,静环网格数确定为240 523个,动环网格数确定为361 207个。
1.3 边界条件
1.3.1 流体域边界条件
模拟密封端面间SCO2流体流动时,为了计算准确,此处笔者调用REFPROP数据库的二氧化碳真实物性数据进行加载,采用5%湍流强度的SST湍流模型,固体壁面设置无滑移。
流体域边界条件如图4所示。

图4 流体域边界条件图
将流体膜与动环接触面定义为旋转域,并给定转速,与静环接触面定义为静止域;在流体进口处设置压力入口,并给定总压,出口处设置压力出口,并给定大气压,径向双侧面设为周期性边界。
1.3.2 固体域边界条件
(1)力边界条件
以截面图表示密封环所受外力情况,则密封环受力分析图如图5所示。

图5 密封环受力分析图PS—单位面积弹簧力,大小为0.05 MPa;Pi—密封腔内SCO2压力;Pr—二氧化碳流体膜压,大小根据流体域的计算结果加载;Po—外界大气压力
此处按图5施加各个力的边界条件,同时在静环的MF边界和动环的TU、IJ边界添加轴向位移约束,并对动环施加工作转速。
(2)热边界条件
密封运转时,产热源主要包括端面间SCO2流体的粘性剪切热和动环带动周围流体的搅拌热。这些热量由动环和静环传递给周围的流体和辅助元件。与动静环接触元件材料的热传导系数较小,可视为绝热边界,泄漏带走的热量和流体带入的热量相互抵消。
接下来进行粘性剪切热计算。动静环高速运转时,端面间SCO2因粘性剪切产生的热量为[16]:
(1)
式中:qi—热流密度,qi=μr2ω2/hi,w·(m2)-1;μ—二氧化碳粘度,pa·s;ω—旋转角速度,rad·s-1;ro—密封面外半径,m;ri—密封面内半径,m;hi—二氧化碳流体膜厚度,m。
下面进行搅拌热计算。流体的搅拌热可分为圆盘搅拌热QA1和圆柱搅拌热QA2[17]。
(2)
当旋转圆柱雷诺数Reω=ωsr·rm/v>10 000时,圆柱搅拌热QA2为:
(3)
式中:r6—动环外半径,m;rh—密封腔体内径,m;l1—动环当量轴向长度,m;k—密封环径向间隙系数,k=2.4-1.4e-Sr/rm;Sr—动环外径与密封腔内径的距离,m;rm—动环外径与密封腔体平均半径,m。
再进行动静环热量分配。由于动静环材料、形状均不同,比热容和导热系数也不一样,热量在动静环的分配量也有所差异。根据热稳态温度计算式,动静环端面热量的分配公式[18]为:
T=q(h1-y)λ0
(4)
式中:T—密封环不同轴向位置的温度,℃;q—热流密度,w·(m2)-1;λ0—密封环导热系数,w·(m·k)-1;h1—密封环轴向长度,m;y—距离密封端面的长度,m。
最后进行对流换热系数计算。根据密封环与周围流体的相对运动方式,可将对流换热方式近似分为3类:第一类是强制对流换热,如动环与SCO2流体的对流换热;第二类是自然对流,如静环与SCO2流体的对流换热;第三类是介于二者之间,如静环与空气的对流换热。
换热系数经验公式[19,20]如下:
(1)第一类对流换热系数为:
(5)
式中:α1—对流换热系数,w·(m2·k)-1;λ—二氧化碳流体的热导率,w·(m·k)-1;D6—动环外圆直径,m;Rea—流体轴向绕流效应雷诺数,Rea=UD6/v;Rec—流体搅拌效应雷诺数,Rec=ωD62/v;Pr—普朗特数,Pr=μCp/λ;v—流体运动粘度,m2·s-1;U—密封环附近流体轴向流速,m·s-1;Cp—流体比热容,kJ·(kg·K)-1。
(2)第二类对流换热系数为:
(6)
式中:ε1—热影响的修正系数;Sr—动环与轴套间隙距离或静环与密封腔内半径距离,m;Re—雷诺数,Re=2VSr/v;V—附近流体轴向速度,m·s-1。
(3)第三类对流换热系数为:
(7)
(8)
式中:Ta—泰勒数;U2—轴或轴套的外径线速度,m·s-1;S—距离密封旋转轴的长度,m;ra—轴或轴套的外半径,m。
SCO2密封环热边界对流换热系数计算结果如表4所示。

表4 SCO2密封环热边界对流换热系数
2 实验及结果分析
笔者采用文献的实验结果,对该热流固耦合计算方法的准确性进行验证。
本文结果与文献实验结果的对比验证如图6所示。


图6 本文结果与文献实验结果对比验证
采用本文的流场数值计算方法对文献[21]的模型和工况进行数值模拟,流体膜径向压力计算结果对比如图6(a)所示,可以看出本文和文献的计算结果有较好的一致性,验证了本文弹性变形计算的准确性;
采用本文的温度场计算方法对文献[22]的模型和工况进行数值模拟,密封端面温度场计算结果对比如图6(b)所示,可以看出本文和文献的计算结果有较好的一致性,验证了本文热变形计算的准确性。
3 研究结果与讨论
3.1 流体膜压力场与密封环温度场分析
在典型工况下,笔者对流体膜的压力场和密封环的温度场进行求解,得出的计算结果云图如图7所示。

图7 计算结果云图
由图7(a)流体膜压力场云图可知:流体膜在槽区出现了明显的压力上升,压力最高点为11.1 MPa出现在螺旋槽的槽根处,这是由于动环旋转后,高压侧流体泵入螺旋槽,在槽根处的流体受到压缩而产生的动压,导致槽根处有明显的高压区;
由图7(b)静环温度场可知:静环温度分布相对均匀,因为静环热导率高,剪切热和高温流体向静环内部迅速传热,而静环与周围介质对流换热系数低,散热速率较慢,所以静环整体温差较小;
由图7(c)动环温度场可知:动环端面温度最高,内径侧温度最低,因为动环外径侧与周围高温SCO2流体对流换热系数高,传热速率较快,内径侧与大气对流换热系数低,散热相对较慢,且动环热导率低,达到热平衡时外侧高温流体传热和端面剪切热没有及时传到内径处,造成动环温差明显。
3.2 端面热弹变形结果分析
对于密封性能而言,端面的变形锥度是关键影响因素。端面变形锥度的大小等于端面轴向变形最大值与最小值之差与端面宽度的比值,该值越小说明端面越接近平行平面,密封的运转条件越好。
为方便说明,笔者以密封端面内径变形为基准,建立坐标系,由静环端面AB边指向静环背面EF边为轴向正方向,沿半径提取端面的相对轴向变形,研究端面热弹变形规律。
在典型工况下,密封环端面轴向热弹变形的计算结果如图8所示。

图8 密封环端面轴向热弹变形计算结果
3.2.1 端面热变形分析
由图8(c)的密封环端面热变形曲线可知,静环的内外径相对热变形量很小,端面热变形锥度仅为0.32×10-4,说明高温热变形对静环端面变形锥度影响很小;动环的内外径相对热变形量较大,端面热变形锥度为3.40×10-4,因为动环基体和覆层材料线膨胀系数不同,且动环导热率低,导致整体温差大,说明使用导热率高的材料有利于减小高温下动环热变形。
3.2.2 端面弹性变形分析
由图8(c)的密封环端面弹性变形曲线可知,静环端面弹性变形锥度为2.80×10-4,这是因为静环外径处流体膜压对端面轴向变形的抑制作用较强,端面变形为正锥度;动环端面弹性变形锥度为-4.49×10-4,比静环大62%,这是因为动环端面除了受压差作用外还受到转速离心力的作用,且离心力产生的端面变形较大。
3.2.3 端面热弹变形分析
由图8(c)的密封环端面热弹变形曲线可知,静环端面热弹变形锥度为3.09×10-4,仅比弹性变形锥度增大了12%,说明静环端面变形锥度主要由弹性变形引起。因此,在设计上应使用弹性模量大的材料减小弹性变形,从而控制静环的热弹变形锥度。
动环端面轴向热弹变形位于热变形和弹性变形之间,说明热变形和弹性变形对动环端面轴向变形作用方向相反。由于高转速下离心力抑制了端面的热变形,导致端面热弹变形锥度比弹性变形锥度减小了76%,比热变形锥度减小了68%。因此,在设计条件下,利用其热变形与弹性变形互相抑制关系能有效地减小动环热弹的总变形。
3.3 端面热弹变形影响因素分析
3.3.1 转速对端面变形影响
为研究转速对端面变形影响,此处笔者选取密封从静止状态启动到典型工况转速50 000 r·min-1范围内的转速进行研究。
转速对密封端面变形的影响如图9所示。


图9 转速对密封端面变形影响
由图9(a)可知:动环转速为50 000 r·min-1时的端面弹性变形锥度比静止状态增大了4倍左右,但方向相反,说明转速离心力与压差对动环轴向弹性变形的作用方向相反,且转速影响大;动环端面弹性变形锥度绝对值随转速升高先减小后增大,且逐渐由正锥度转为向负锥度,说明低转速时,端面弹性变形以压差作用为主导,随转速升高,端面变形以转速离心力为主导;
由图9(b)可知:密封环端面热变形和锥度随转速升高而小幅度增大。这是因为随着转速的增加,流体的剪切热增大速率逐渐增大,使得密封环温度升高的同时,温差也在逐渐增大,但是相对于端面总体的变形大小,转速变化引起的端面轴向热变形和锥度变化量均较小;
由图9(c)可知:转速使动环端面热弹总变形向负锥度方向变形,静环向正锥度方向变形;随转速增大,动静环之间的最大轴向间隙先减小后增大。将其与图9(a,b)进行对比可知:静环的热弹变形的变化主要由热变形引起;动环的热弹变形在低转速时,热弹变形以压差产生的弹性变形和温度产生的热变形为主导,随转速升高,端面变形以转速产生的弹性变形为主导。
所以在高转速下,通过利用离心力产生的弹性变形平衡温度和压差产生的热弹变形,能使动静环端面达到近乎平行状态,有利于密封的稳定工作。
3.3.2 压力对端面变形影响
压差主要影响密封端面的弹性变形和热弹总变形,对热变形几乎没有影响。
压力对密封端面变形的影响如图10所示。

图10 压力对密封端面变形的影响
由图10(a)可知:静环端面最大轴向弹性变形和端面变形锥度均随压力升高而增大,这是由于流体压力越大,静环外径侧向受到的流体膜压越强,导致压差产生的变形越大;动环端面最大轴向弹性变形和端面变形锥度均随压力升高而减小,因为压力与离心力对动环端面变形作用方向相反,压力越高,其对离心力的抵消作用越强,但动环端面材料弹性模量大,所以压力改变时,端面轴向弹性变形变化量较小;
由图10(b)可知:压差使动静环端面热弹变形向正锥度方向变形;随着压力增大,动环的最大轴向热弹变形以0.11 μm/MPa减小,静环最大轴向热弹变形以0.27 μm/MPa增大。所以高转速下,压差越大,动环的变形锥度越小,但是静环的变形锥度会增大,且变化量大于动环,导致动静环端面最大间隙加大,密封稳定运转的端面条件越恶劣。
3.3.3 介质温度对端面变形影响
介质温度主要影响密封端面的热变形和热弹总变形,对弹性变形几乎没有影响。本文在超临界温度以上340 K到430 K范围内研究介质温度对端面变形的影响。
介质温度对密封端面变形的影响如图11所示。

图11 介质温度对密封端面的影响
由图11(a)可知:动环端面轴向热变形和锥度均随着介质温度的升高而增大。这是由于动环覆层与基体材料不同,线膨胀系数有所差异,温度越高产生热变形越大,两者膨胀量相对差值越大,即端面热变形锥度越大;介质温度升高,静环端面热变形锥度基本不变,说明介质温度对静环热变形影响较小;
由图11(b)可知:介质温度使动静环端面热弹变形向正锥度方向变形。随介质温度的升高,静环热弹变形锥度基本不变,动环最大轴向热弹变形以0.036 μm/K减小,热弹变形锥度降低75%,动静环最大轴向间隙减小3.22 μm,这是因为动环的热变形抑制了以转速为主导的弹性变形。所以高转速下,介质温度越高,动环端面热弹变形锥度越小,动静环最大轴向间隙减小,密封稳定运转端面条件越好。
4 结束语
本文以超临界二氧化碳螺旋槽动压密封为研究对象,对密封动静环的端面热弹变形进行了整体分析,求解了密封端面的热弹变形;同时,考虑了粘性耗散和真实气体效应,提高了数值计算的准确性,研究了操作参数对密封端面热弹变形的影响规律。
研究结论如下:
(1)在高压下,静环的端面热弹变形以压差产生的弹性变形为主导,占热弹变形锥度的89%,宜采用高弹性模量材料减小变形。在低转速时,动环以压差产生的弹性变形和温度产生的热变形为主,宜减小密封环的温差以减小端面变形。随转速升高,动环端面热弹变形以转速产生的弹性变形为主导,宜依靠动环热变形与弹性变形互相抑制关系减小端面热弹总变形。在典型工况下密封的设计中,静环推荐使用高弹性模量材料,动环推荐使用热导率高的材料以减小端面变形;
(2)动静环的端面热弹变形在压力和温度作用下向正锥度方向变形。转速使动环端面向负锥度方向变形,使静环端面向正锥度方向变形。密封环的端面最大轴向间隙与介质温度呈线性关系增大,与压力呈线性关系减小,转速则使其先减小后增大;
(3)研究结论可为高温、高压和高速工况下,超临界流体的机械密封设计提供理论依据。
