多类型滑动轴承性能对比分析及其油膜温度试验研究*
2021-04-22王晓红
王晓红,常 山,陈 涛
(中国船舶重工集团公司 第七〇三研究所,黑龙江 哈尔滨 150078)
0 引 言
船舶传动装置传动形式多样,运行工况较多[1];同时,传动装置中轴的转速与功率变化范围较宽,导致载荷的大小与方向多变。因此,传动装置中同一轴承均需满足多种承载要求。另外,同一传动装置的齿轮轴转速与扭矩差别较大,支承齿轮轴的轴承可能存在低速重载或高速轻载的使用条件,使得其轴承的类型也多种多样。
常用的船舶传动装置轴承类型有圆柱形、椭圆、可倾瓦[2]等,每类轴承适应的转速和载荷范围不同。Kingsbury、John Crane等国外知名轴承公司样本中,给出不同轴承类型推荐的应用转速、比压及稳定性排序等。ISO标准[3]、国标[4]则给出了轴承最小油膜厚度及巴氏合金材料最高温度限定条件。
但具体工程应用选型时还会面临一些问题,各类型轴承推荐的应用范围多有交叉,关于轴承运行温度等性能没有翔实的对比数据。
对于各类型轴承之间的对比,不同学者做过许多研究工作[5-9],但大多研究仅限于理论研究,而对于船舶传动装置多种类型轴承对比方面的研究,乃至试验研究验证的则很少。
本文从船舶传动装置应用特点出发,针对轴承类型多样、轴承转速及载荷跨度大的应用情况,对比分析常用的圆柱形轴承、椭圆轴承及可倾瓦轴承性能,研究不同类型轴承在船用转速和载荷条件下性能的变化规律,并对几种类型轴承温度场进行试验对比研究,为船舶传动装置轴承类型选取提供依据。
1 计算模型
1.1 滑动轴承几何关系
此处以三油叶轴承为例,笔者介绍轴承参数的关系(可以拓展到所有轴承几何关系)。
轴承的几何关系如图1所示。
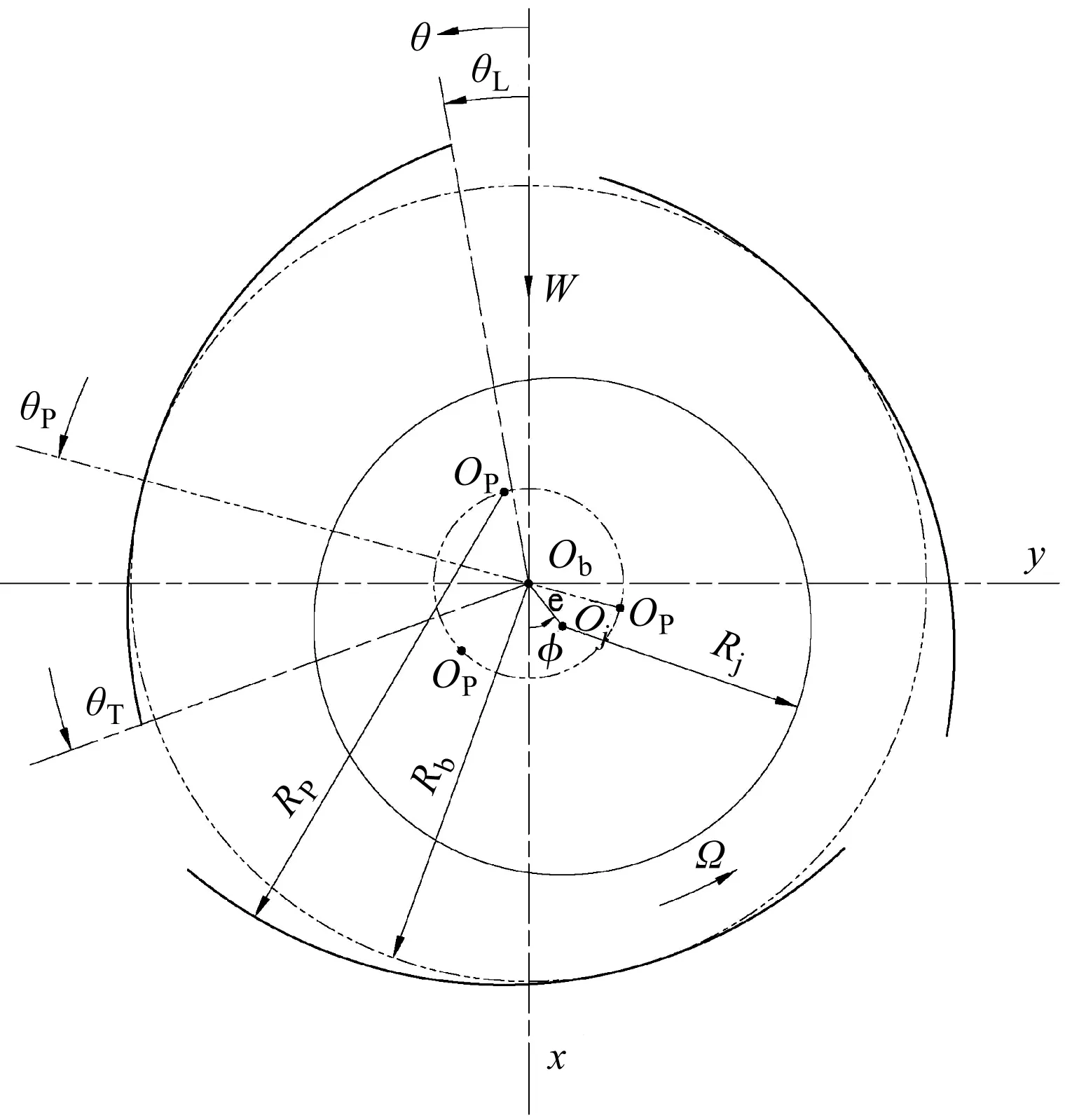
图1 轴承几何关系Ob,Rb—轴承中心,轴承装配半径,m;OP,RP—轴瓦中心,轴承加工半径,m;Oj,Rj—轴中心,轴半径,m;θL,θT—轴瓦起始、终止角,°;θp—支撑角,°
由图1的几何参数可以得出轴承的主要参数如下:
Cb=Rb-Rj
(1)
Cp=Rp-Rj
(2)
(3)
f=(θp-θL)/(θT-θL)
(4)
式中:Cb—轴承装配间隙,m;Cp—轴承加工间隙,m;m—轴承预负荷;f—支撑特性参数。
对于圆柱形轴承,Ob,Op重合,Rp=Rb;
对于椭圆轴承,Ob,Op不重合,Rp>Rb;对于可倾瓦轴承,常用3个~5个油叶,Ob,Op可重合,也可不重合,Rp≥Rb,并增加摆角自由度。
1.2 基本方程
笔者根据几何关系,建立轴承油膜厚度的关系式后,计算滑动轴承性能。该过程主要求解以下方程:
(1)雷诺方程:
(5)
式中:p—油膜压力,Pa;h—油膜厚度,m;μ—润滑油动力粘度,Pa·s;Rx,Rz—紊流因子;U—轴的旋转速度,m/s;t—时间,s;x,z—周向、轴向坐标。
(2)能量方程:
(6)
式中:ρ—滑油密度,kg/m3;Cp—比热容,J/(kg·℃);k—润滑油传导系数;qx,qz—周向,轴向单位体积流量,m3/h;T—油膜温度,℃;τ—剪切应力,Pa。
其中:
(7)
(8)
(9)
式中:Cf—紊流因子,层流时为1;紊流时由下式确定:
Cf=1+0.001 2Re0.94
(10)
式中:Re—雷诺数。
(3)温粘关系:
loglog(v+C)=A-Blog(T)
(11)
μ=ρv
(12)
式中:v—运动粘度,mm2/s;A,B—用已知温度点下的粘度进行求解;C—在运动粘度小于2.0 cSt时,取0.7。
(4)承载能力:
(13)
式中:Fx,Fy—x,y方向载荷,N;L—轴承宽度,m。
(5)动态性能:
在静平衡位置处,微小扰动下,力平衡方程为:
(14)
式中:Fx0,Fy0—静平衡位置x,y方向静态载荷,N;K—轴承刚度,N/mm;C—轴承阻尼,N·s/mm。
1.3 边界条件与求解方法
此处的压力分布采用雷诺压力边界条件,即结构边界条件:
(15)
θ=θLp=p0
(16)
自然边界条件为:
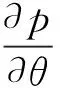
(17)
能量方程的边界条件为:润滑剂入口处温度为供油温度,求解时以此作为初值,应用步进方法求解温度场;入油边考虑冷热油混合作用。
此处采用有限差分方法,联立求解雷诺方程、能量方程与温粘方程,求得压力分布与温度分布,进而求解轴承的静态和动态性能。
2 算例及计算结果对比分析
2.1 转速对各类型轴承性能影响
为了研究转速单一因素对性能的影响,本文选定轴承参数:直径200 mm,宽径比1,间隙比为0.002,椭圆轴承m=0.5,可倾瓦轴承m=0.5,比压2 MPa,转速范围涵盖船舶传动装置大部分转速范围。
最高温度对比如图2所示。
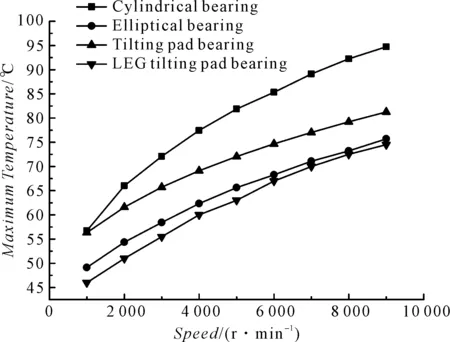
图2 最高温度对比
承载能力对比如图3所示。
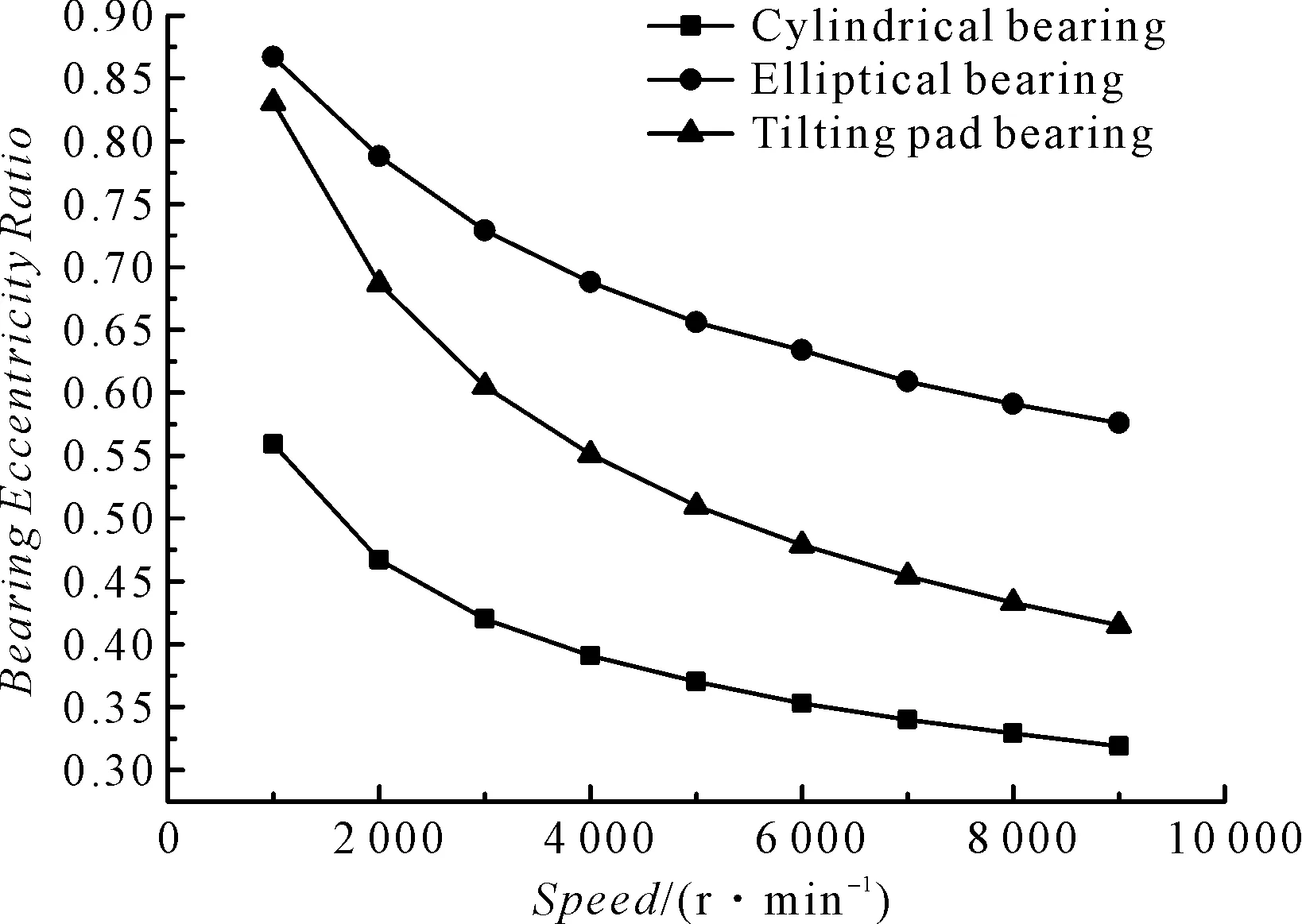
图3 承载能力对比
功耗对比如图4所示。
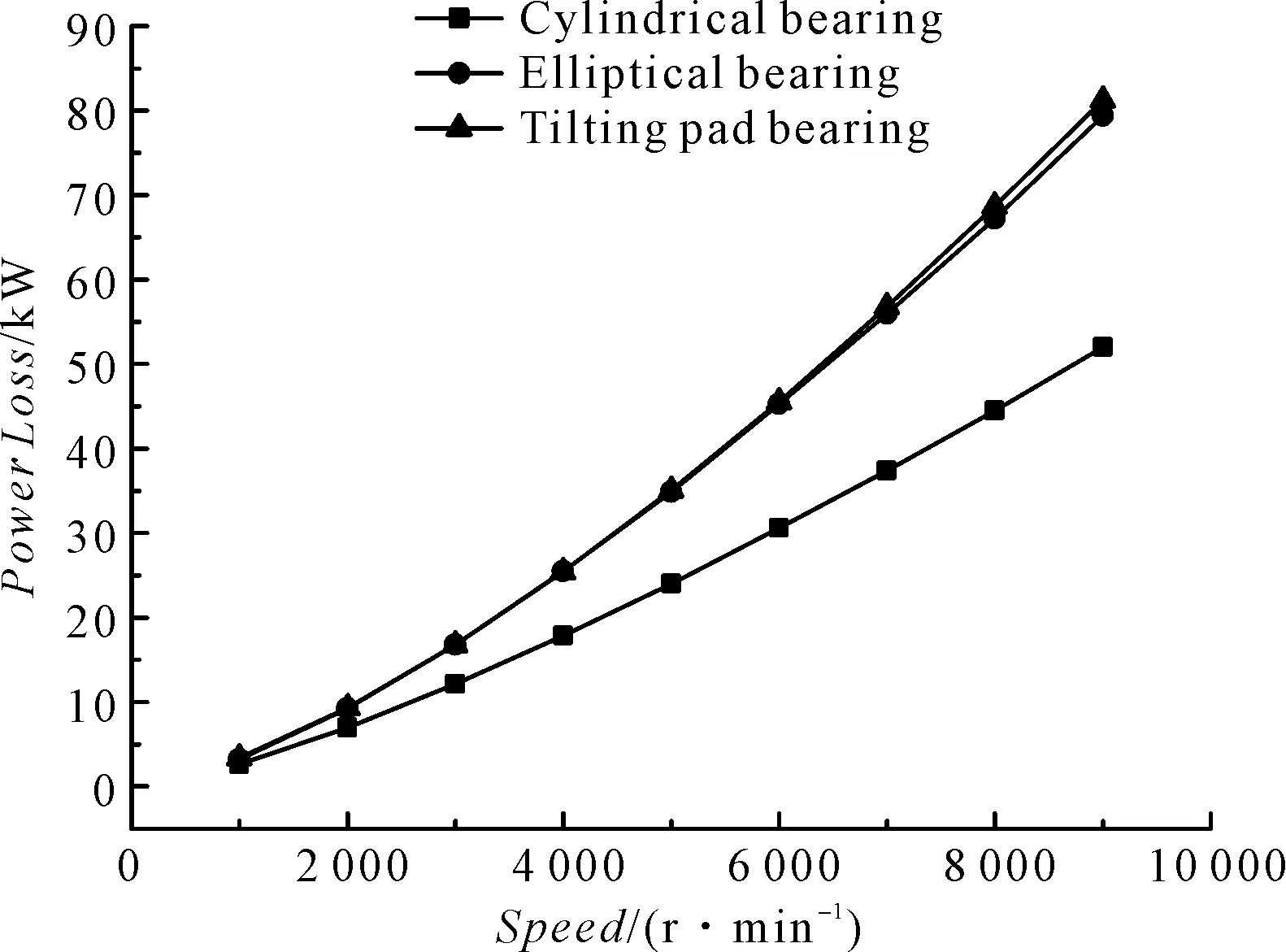
图4 功耗对比
流量对比如图5所示。
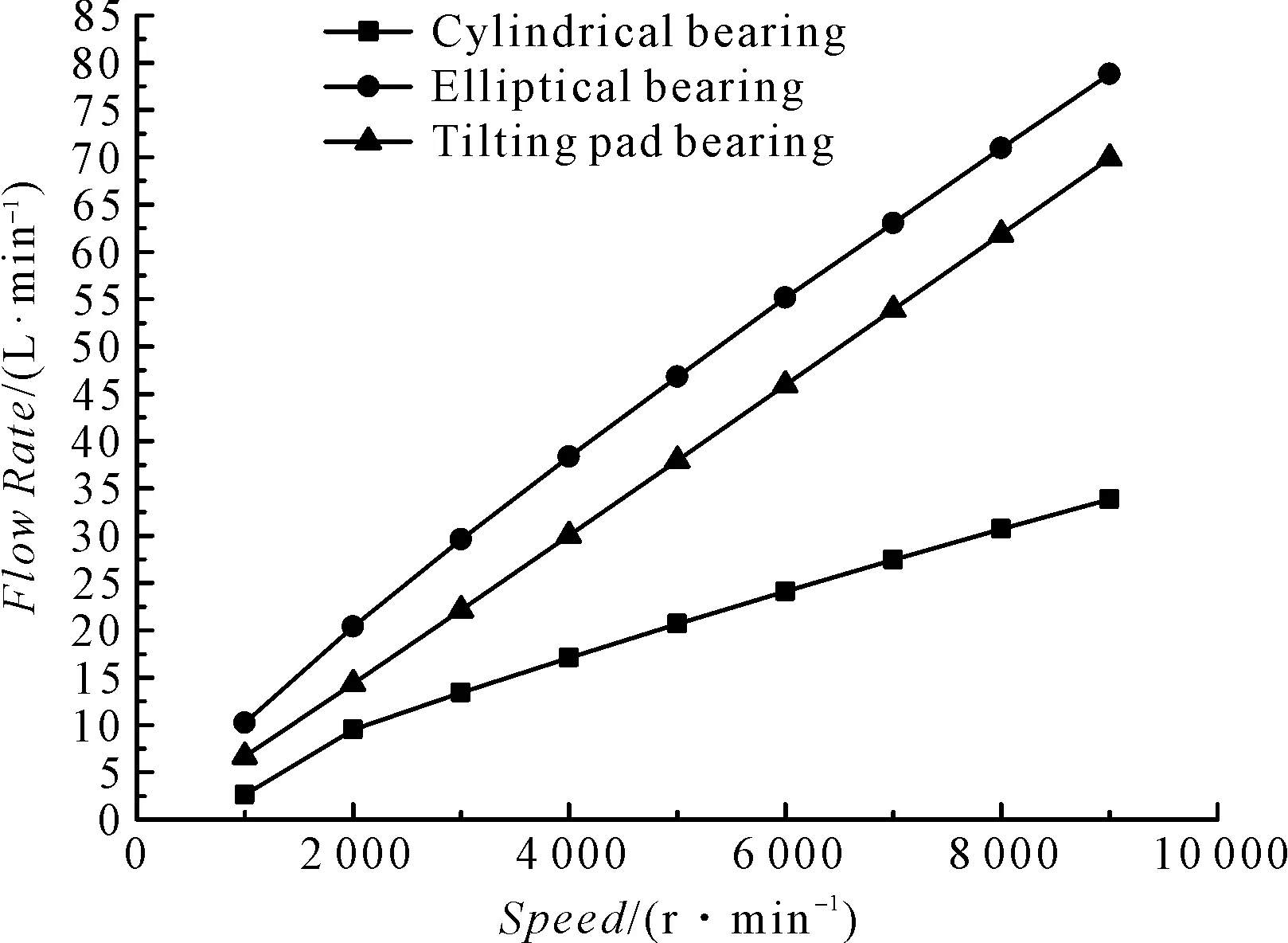
图5 流量对比
根据以上的对比图可知,转速对各类型轴承静态性能影响情况如下:圆柱形轴承最高油膜温度比其他类型轴承更高,尤其在高转速时更加明显,圆柱形轴承比椭圆轴承最高温度高出19 ℃,圆柱形轴承承载能力最大,功耗、流量也更小;
另外,由于可倾瓦轴承结构的特殊性,可以通过单独供油降温的方式,并由图2可知,单独供油的可倾瓦轴承可以获得更低的温度。
动态性能对比如图6所示。
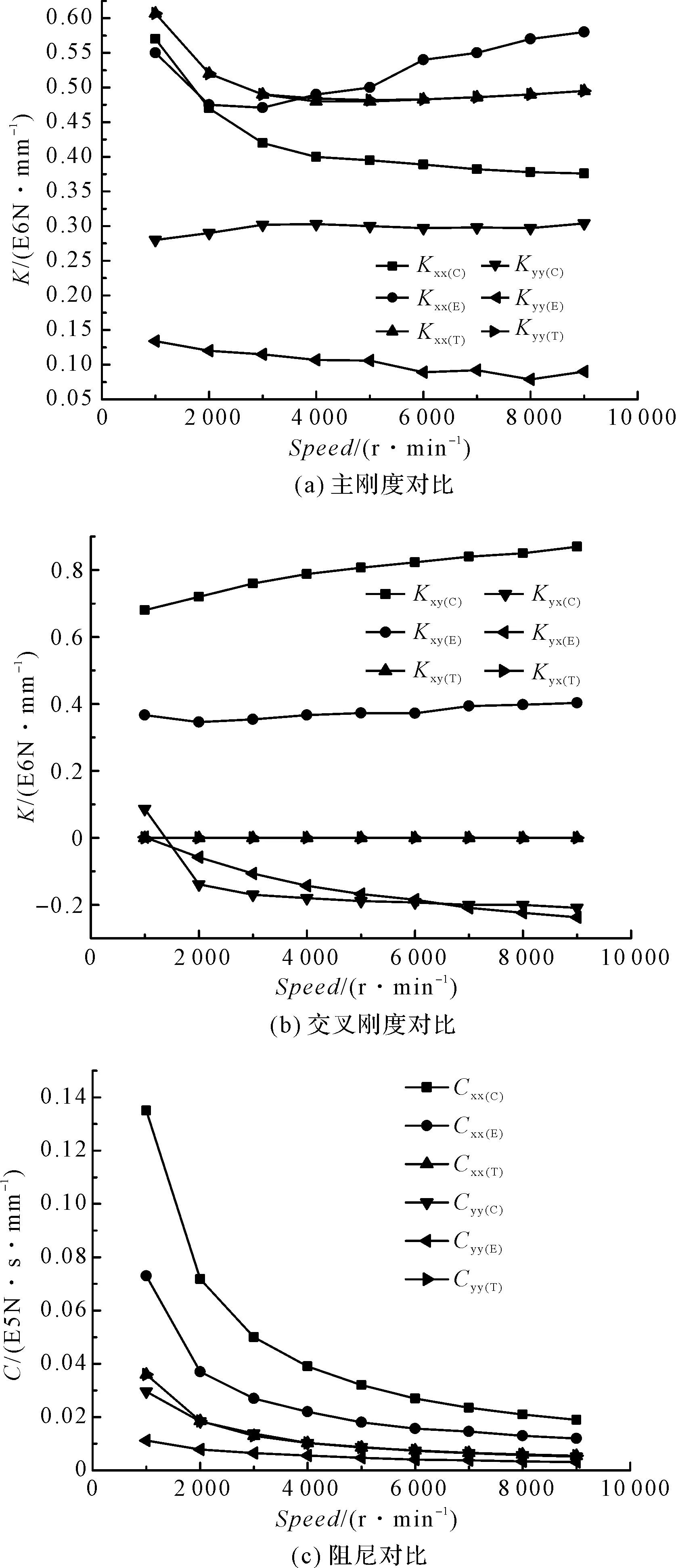
图6 动态性能对比C—圆柱形轴承;E—椭圆轴承;T—可倾瓦轴承
以上对比情况可知,转速对各类型轴承刚度和阻尼的影响为:受力方向的主刚度Kxx,圆柱形轴承略低于其他类型轴承,但均在同一数量级,高速时圆柱形轴承主刚度有下降趋势,而椭圆及可倾瓦轴承没有明显的下降趋势。
值得注意的是,四瓦可倾瓦轴承交叉刚度为0,交叉刚度存在是滑动轴承失稳的重要原因,同时,可倾瓦轴承瓦块可以摆动以适应外部激励变化,因此,其稳定性远优于其他类型轴承,椭圆轴承稳定性优于圆柱形轴承。
另外,圆柱形轴承与椭圆轴承非受力方向的主刚度Kyy明显低于受力方向主刚度Kxx,但可倾瓦轴承却相同;圆柱形轴承的阻尼略高于其他类型轴承,转速越高相差越小,随转速增加,圆柱形轴承阻尼减小明显。
2.2 载荷对各类型轴承性能影响
为了研究载荷单一因素对性能的影响,此处选定轴承参数为:直径200 mm,宽径比1,间隙比为0.002,椭圆轴承m=0.5,四瓦可倾瓦轴承m=0.5,转速4 000 r/min;比压选取涵盖船舶传动装置滑动轴承大部分载荷范围。
最高温度对比结果如图7所示。
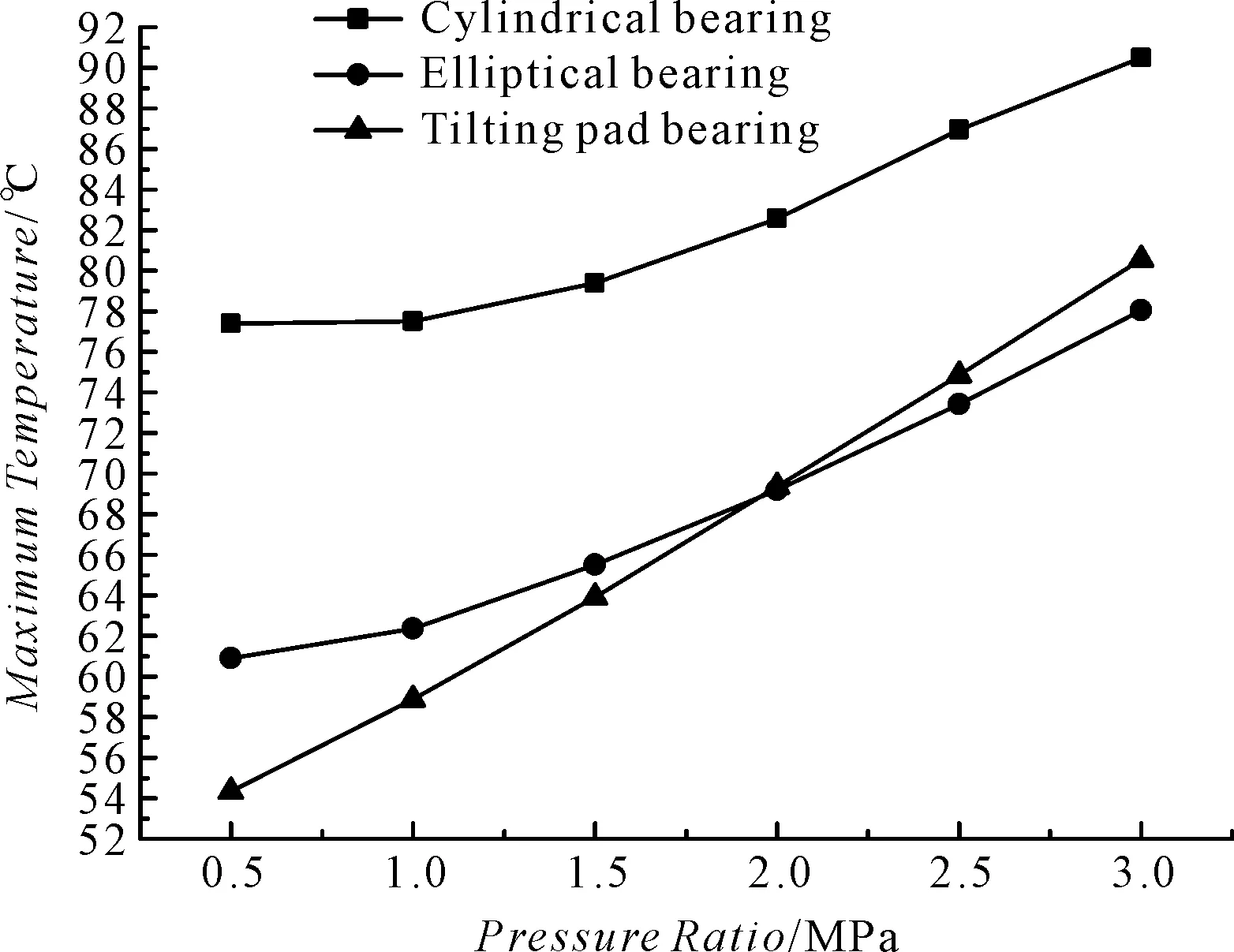
图7 最高温度对比
承载能力对比结果如图8所示。
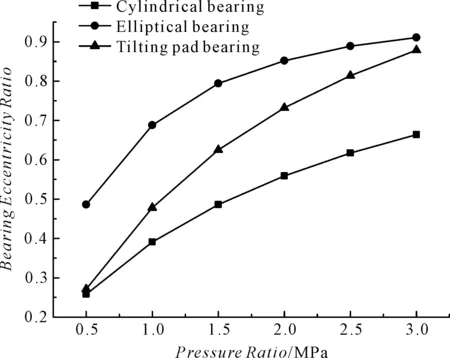
图8 承载能力对比
功耗对比结果如图9所示。
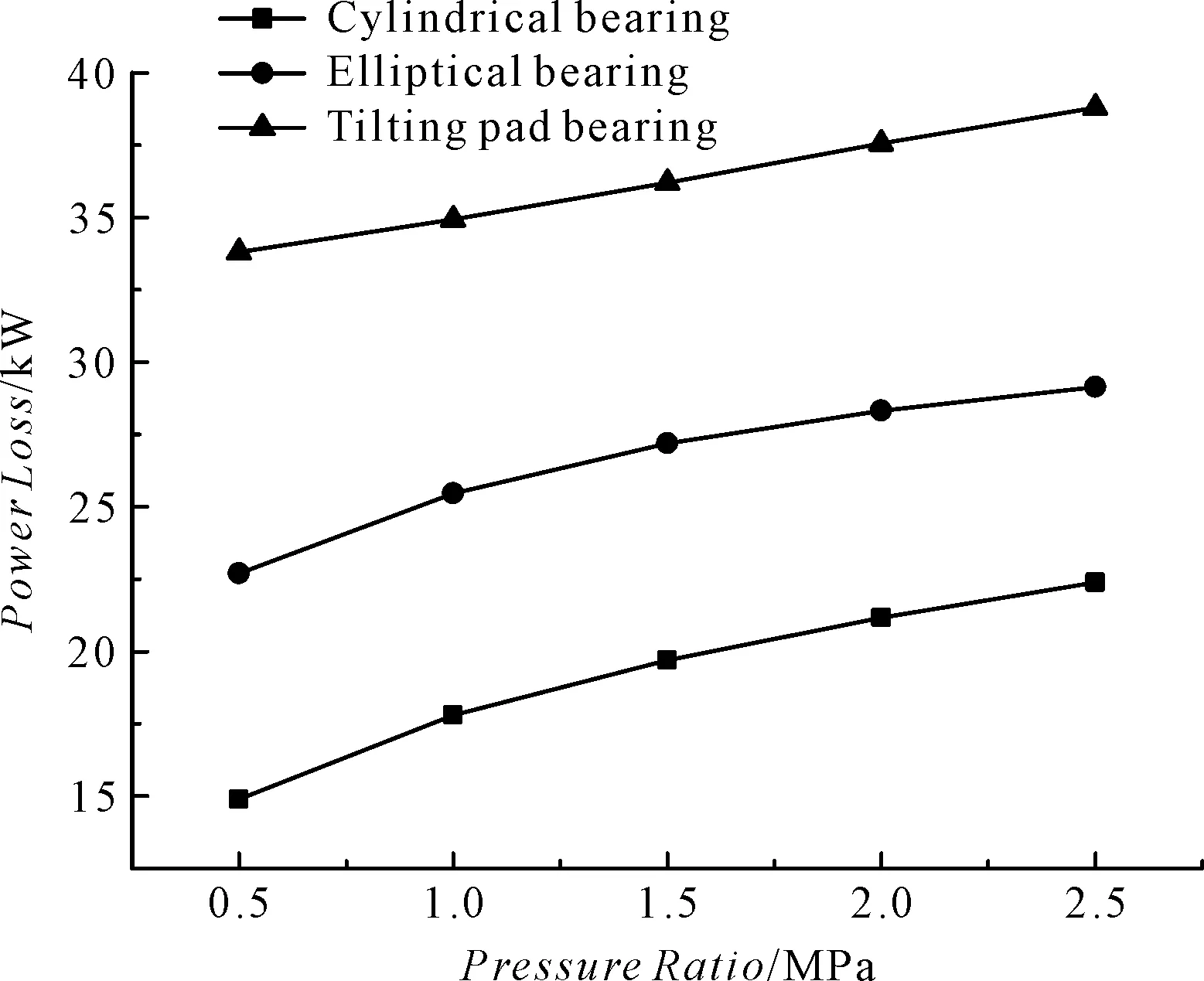
图9 功耗对比
流量对比如图10所示。
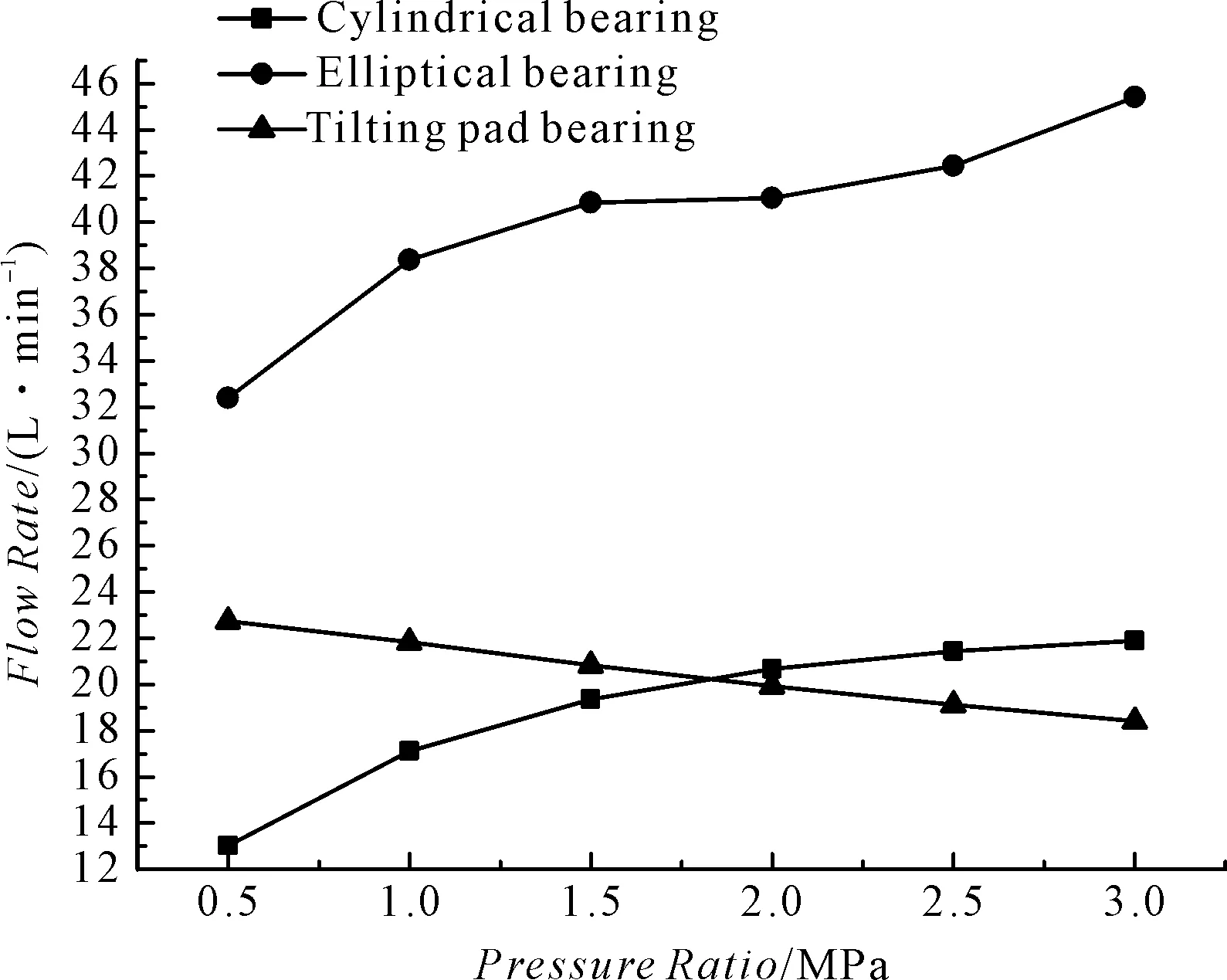
图10 流量对比
载荷对各类型轴承静态性能影响:在各个比压范围内,圆柱形轴承最高温度均高于其他类型轴承,最高温度高出其他轴承13 ℃左右,并且该数值基本变化不大,圆柱形轴承承载能力最高,在功耗方面,圆柱形轴承优于椭圆轴承,椭圆轴承优于可倾瓦轴承,并且在各个比压范围趋势比较一致,椭圆轴承流量最大,圆柱形轴承与椭圆轴承随着比压的增大,流量缓慢增加,但可倾瓦轴承流量有所下降。
动态性能对比结果如图11所示。
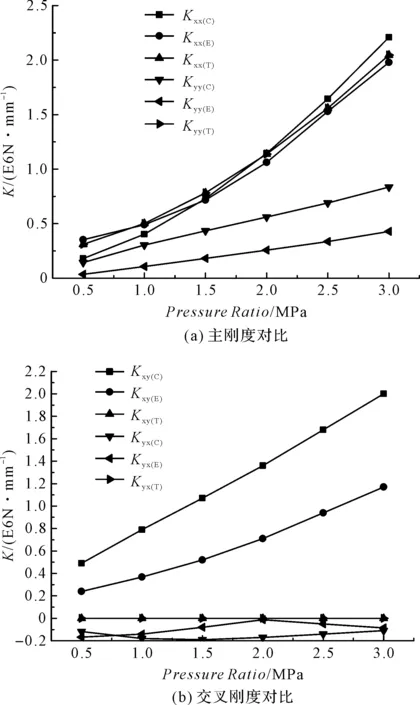
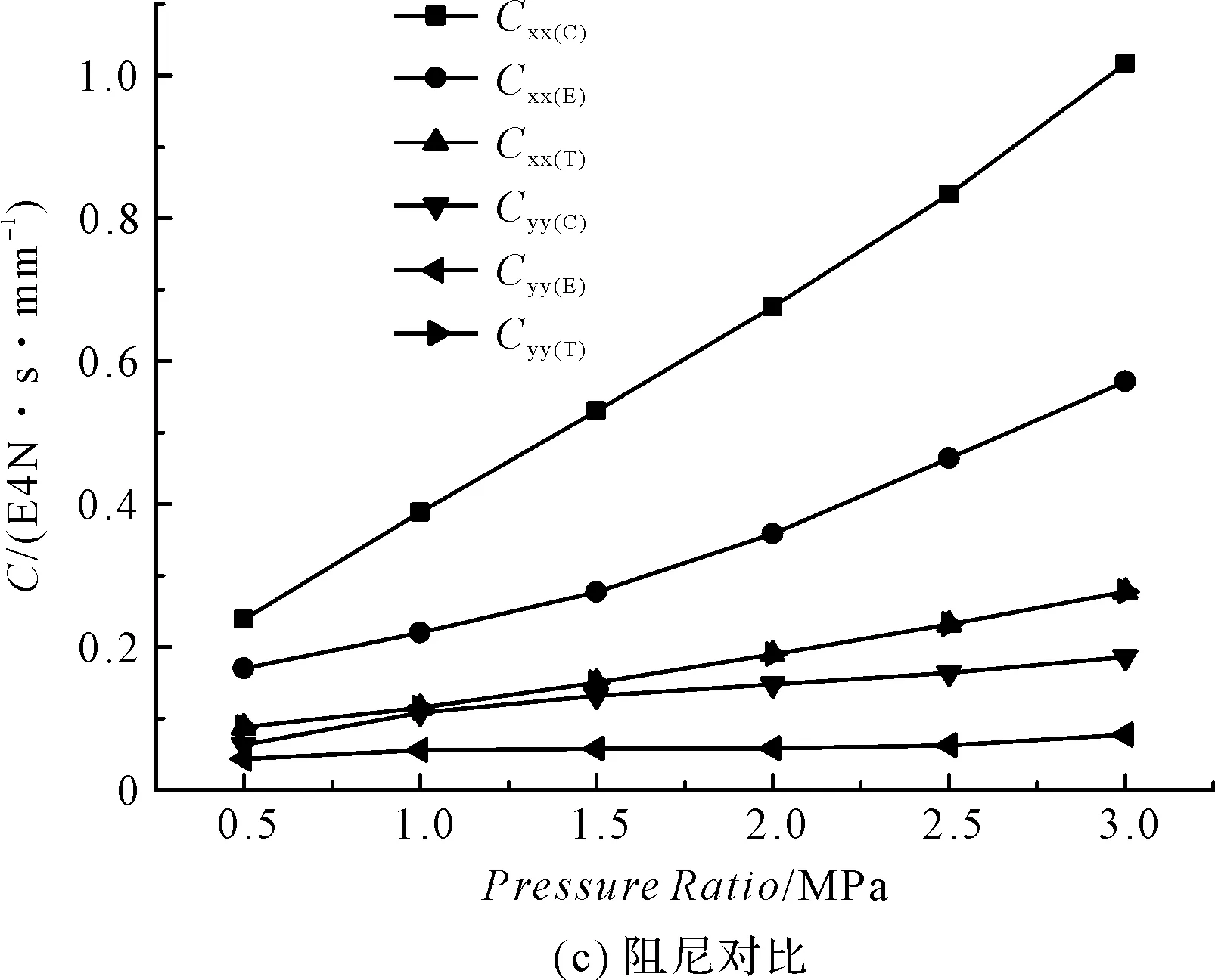
图11 动态性能对比
转速一定下,3种轴承载荷方向主刚度比较接近,随着比压增大,各轴承刚度值增加明显,圆柱形轴承与椭圆轴承Kyy明显地低于Kxx,可倾瓦轴承两个方向主刚度一致,四瓦可倾瓦交叉刚度为0,稳定性最好,圆柱形轴承的阻尼最大,尤其随着比压增大,趋势越明显。圆柱形轴承与椭圆轴承Cyy明显地低于Cxx,可倾瓦轴承则相同,随着比压增大,圆柱形轴承与椭圆轴承阻尼增加明显,而可倾瓦轴承阻尼变化不大。
3 温度场试验对比分析
3.1 试验装置
本文分别通过试验方式,分析转速对上述3种类型轴承温度场的影响。
其中,轴承直径200 mm,宽度200 mm,间隙比0.002,轴承载荷17 000 N。
试验台的布置图如图12所示。
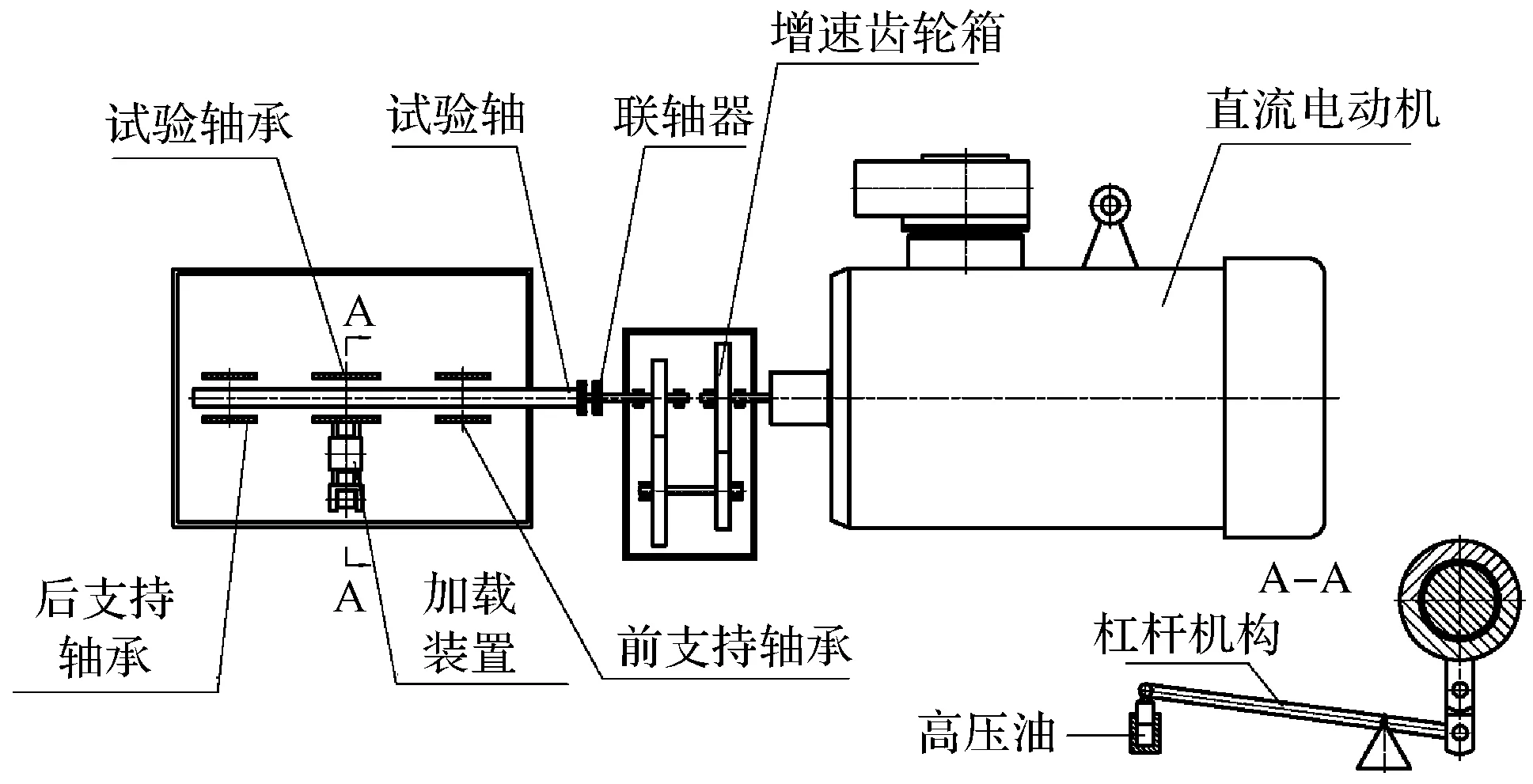
图12 试验台布置图
在倒置式试验台上,笔者进行轴承油膜温度试验。其中,液压加载通过试验轴承座作用到试验轴承上,调节液压缸的供油压力可以改变轴承的载荷,这样试验过程中轴承上瓦受力,电机通过增速箱改变试验轴的转速,可以满足试验中转速的要求。
3.2 试验结果与分析
轴承的油膜温度测点布置于其上部轴承承载区,一共布置了多个测点,来测定轴承油膜的最高温度。
试验轴承测点测得的温度如表1所示。
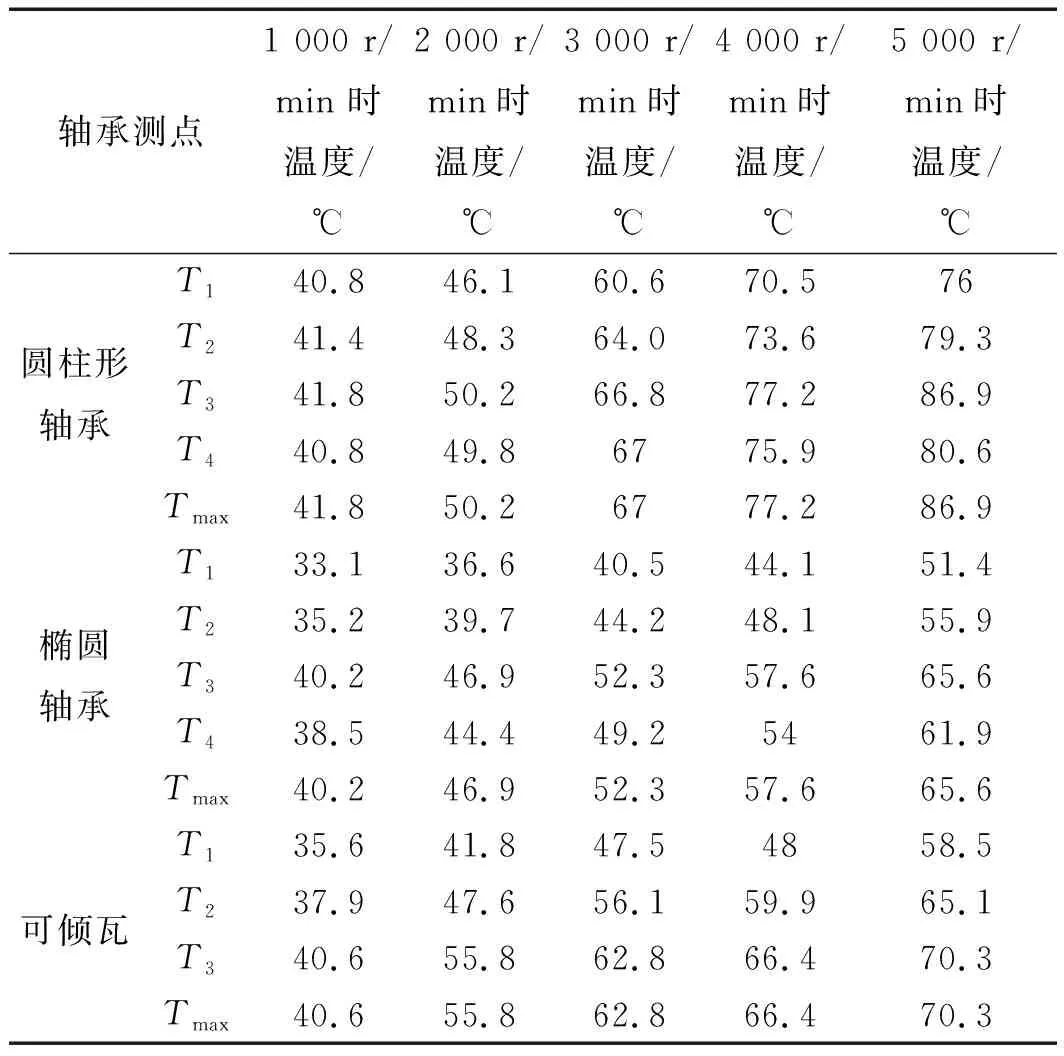
表1 试验轴承测点温度
由表1可知:圆柱形轴承油膜温度高于椭圆轴承和可倾瓦轴承,并随着转速的增高,差距变得更大,最大可以达21.3 ℃。
以上这个趋势与上述的理论计算结果一致。
4 结束语
本文分别计算和分析了转速及载荷对各类型船用轴承性能的影响,并通过试验研究了转速对不同类型轴承油膜温度的影响。
研究结果表明:
(1)圆柱形轴承最高油膜温度高于其他两种类型轴承,差距随转速升高而增大,在转速达到5 000 r/min时,各类型试验轴承的最高油膜温度相差达21.3 ℃;
(2)圆柱形轴承承载能力较其他类型明显高,功耗与流量也优于其他类型轴承;
(3)各类型轴承主刚度随载荷变化明显,随着转速变化量较小,其中,圆柱形轴承交叉刚度较大,可倾瓦轴承交叉刚度最小。
因此,在船舶传动装置轴承选型时,应优先选择圆柱形轴承;只有当转速过高,圆柱形轴承温度过高和存在失稳风险时,才应该结合转子计算结果,选择其他类型的轴承。
