基于ANSYS-Workbench的流固耦合作用下输油管道模态分析
2021-04-22陈为化张伟杰魏子杰
李 青 ,陈为化,张伟杰 ,张 敏 ,魏子杰
(1. 华北科技学院 机电工程学院,北京 东燕郊 065201;2. 华北科技学院 河北省矿山设备安全监测重点实验室,北京 东燕郊 065201)
0 引言
输油弯管在各个领域中都有重要的应用。管道内流体参数的变化产生管道振动,引起共振甚至断裂,由于对于管道系统中的流固耦合的作用不够重视,使得流固耦合作用造成的各种领域里的损害时常发生。为了设计和制作出更加安全可靠的管道机械,对流固耦合作用下的管道振动分析就变得十分重要[1-3]。
国内外学者致力于研究管道流体在不稳定状况下流固耦合作用问题,M.Kandil建立流体动力学模型和管道运动模型,运用流体与管道的相互作用即双向流固耦合方法,研究了水锤效应在连接处或阀门处的机械振动、流体压力和速度分布,所建立的数值模拟模型通过与前人结果对比得到了验证[4]。李玺研究了流固耦合作用下,壁厚对管道固有频率变化,壁厚的增加使管道固有频率减小,高阶模态频率随壁厚变化趋势大于低阶模态频率的变化趋势[5]。王晓丹研究了密度对流固耦合管道固有频率的影响规律,表明不管是石油还是天然气管道,固有频率与密度大小成反比,天然气的变化幅度相对较小,说明管道中输送流体密度越大,管道的固有频率降低的幅度也越大[6]。卢嘉伟建立了竖直弯管不同转弯角度的有限元模型,随着转弯角度的增加,导致管道固有频率降低,使得流体与管道产生共振的几率增大[7]。周知进研究了不同曲率管道的流固耦合效应,流体在管道弯曲壁面产生的应力导致管道变形,随着弯曲角度的增加,弯管处最大应力先减小后增大再减小的。管道曲率半径的改变会影响管道的受力分布[8]。赵江采用基于双向流固耦合对流体作用下的T 型管模态进行分析,较确切地反映内部流体作用下的管道模态,并对T型管振动剧烈的结合部位进行谐响应分析[9]。
1 理论分析
1. 1 模态分析
模态是机械结构的一种振动特性,模态和振动频率是一一对应的,即每个模态都有特有的固有频率、模态阻尼比和模态振型。模态分析可以获得结构的独有频率,在结构设计时可以避免各种条件下的共振。模态分析是其他动力学研究的基础如响应谱分析、随机振动分析、谐响应分析。无阻尼的模态分析是经典的特征值问题,动力学问题运动方程如下[3,5]:
[M]{x″}+[K]{x}={0}
(1)
式中,[M]为质量矩阵;[K]为刚度矩阵;{x″}为加速度矢量,m·s-2;{x}为速度矢量,m·s-1。
结构的自由振动为简谐振动,即位移为正弦函数,
x=xsin(ωt)
(2)
带入上式得:
([K]-ω2[M]){x}={0}
(3)
1.2 流固耦合
输油管道的流固耦合振动特性是由管道中流体的静压和动压共同作用引起的,当流体的静压和动压相对于管道的临界载荷较小时,管道的固有频率变化较小,输油管道不会发生流固耦合;当管道中流体的静压和动压之和接近管道的临界载荷,输流管道将会发生流固耦合振动,从而引起管道的疲劳破坏[10]。
在很多实际工程的领域中,流体在管道内流动过程中产生的冲击作用会使管道发生变形,而管道的变形会反作用于流体,影响流体的运动状态。这种流体作用于固体,而固体又反过来作用于流体的相互作用叫做流固耦合。流固耦合可以分为单向流固耦合和双向流固耦合。
单向的流固耦合是指先独立地建立流场和固体结构,再将其中一个场求解结果以载荷的形式施加到另一个场中,这样的作用是单向的,只研究流体对固体产生影响,不考虑固体结构改变对流体的作用。双向流固耦合则两者的相互作用都要考虑[3,11]。
流固耦合方程应在流固耦合交界面两侧遵循基本的守恒原则,即应该满足以下条件[7]:(下角标f代表流体,s代表固体)
① 应力相等:τf·nf=τs·ns
(4)
② 位移相等:df=ds
(5)
式中,τf为流体的剪切力矢量;τs为固体的剪切力矢量;nf为流体的节点数;ns为固体的节点数;df为流体的位移;ds为固体的位移。
在 Workbench 对输流管道流固耦合的分析计算中,在流固交界面,流场对固体,固体对流场这两者一直在相互作用。
2 输油弯管的流固耦合模态分析
2.1 模拟方法
流固耦合的仿真分析有单向耦合法和双向耦合法两种方法。因为流场在管道中运动而产生的管道结构变形较小,对流场产生的影响很小,本文采用单向耦合法对结构进行计算。通过 ANSYS-FLUENT 对流场进行分析,将流场分析结果以压力载荷形式作用于管道内表面上,再导入到Modal 中对进行模态分析。
2.2 几何参数
采用ANSYS自带的 Space-Claim建立弯管的三维模型,管道模型如图 1 所示,模型参数见表1,油品从左上端的入口流入,由右下端的出口流出。

表1 管道模型参数

图1 三通管模型图
2.3 材料参数
管道采用普通钢材,密度 7850 kg/m3,弹性模量200 GPa,泊松比0.3。燃油密度960 kg/m3,介质声速1 450 m/s,动力粘度0. 048 Pa·s。
2.4 网格划分
先在模型里将固体抑制,仅对流体部分进行划分,流体区域划分以后,插入膨胀层,将膨胀选项设置为第一层厚度,在下方输入其厚度为0.0002点击生成网格如图2所示,同样,划分固体网格时,将流体域进行抑制,生成网格如图3所示。

图2 流体网格划分

图3 固体网格划分
2.5 流固耦合模态分析流程
在Workbench里选择Fluid Flow(Fluent)、Static Structural 和Modal,将三者进行关联,进行流固耦合作用下的模态分析,如图4所示。
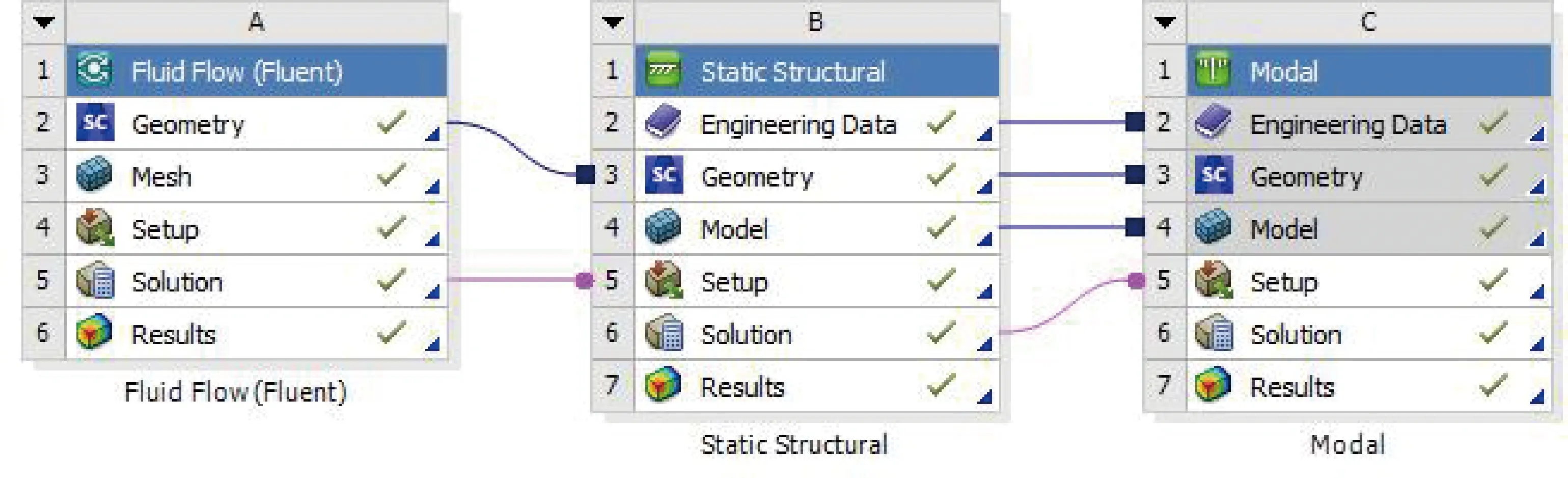
图4 流程图
在Fluent设置为标准的模型(k-epsilon)。在材料库添加燃油(C19H30),将入口设置为速度入口,设置出口为压力出口,残差值设置为0.00001进行计算,设置计算次数为500次。在Static Structural将流体的计算结果以压力载荷的形式施加在管道内壁面,并将入口和出口的设置为固定约束,进行有预应力的模态分析结算,最后进行结果输出,在得到六阶模态的频率和总变形,并与输油弯管的自振频率和振型对比分析。
3 模拟结果
在燃油流速为固定5 m/s,改变管道内压强大小,根据国家标准GB50819-2013陆上油田集输钢制管道设计压力不大于32 MPa,适当扩大研究范围,压力取值范围为0到50 MPa之间,为对比压力和速度变化对振动频率的影响,流体速度对应取0到50 m/s,这个取值范围完全包含实际中输油管道的流体流速大小。图5为流体5 m/s速度分布,图6为将流体计算结果以压强载荷导入到管道内表面的流固耦合界面图。保持燃油流速为5 m/s,不同压强下输油弯管的模态振动见表2。由表2可知,当压力小于0.1 MPa,管道的固有频率与自振频率几乎相同;在1 MPa到15 MPa 取值范围内,压强增值幅度为1 MPa,压强每增加1 MPa,频率有明显的增加;在15 MPa到50 MPa范围内,压强增值幅度为5 MPa,压强每增加5 MPa,频率都有较大幅度的增加。同理,保持燃油的压强为10 MPa的情况下,不同流速下输油弯管的振动模态见表3。由表3可知,保持压强为10 MPa工况下,即使流体流速为0 m/s,管道固有频率比自振频率有明显差异。当流速小于10 m/s 时,改变流速大小对频率几乎没有影响;当流速大于10 m/s,在10 m/s到15 m/s范围内,流速增值幅度为1 m/s,流速每增加1 m/s,频率增加微乎其微;在15 m/s到50 m/s范围内,流速增值幅度为5 m/s,流速每增加5 m/s,频率略有增加,但增加幅度小于压强增值幅度为1 MPa时的改变量,更小于压强增值幅度为5 MPa其固有频率的增加。由此可见对比流速和压强的情况,可以看出来流速对管道固有频率的影响比较小,而压强变化对管道固有频率的影响比较大,这一结论与其他学者[9]的研究结果相吻合。
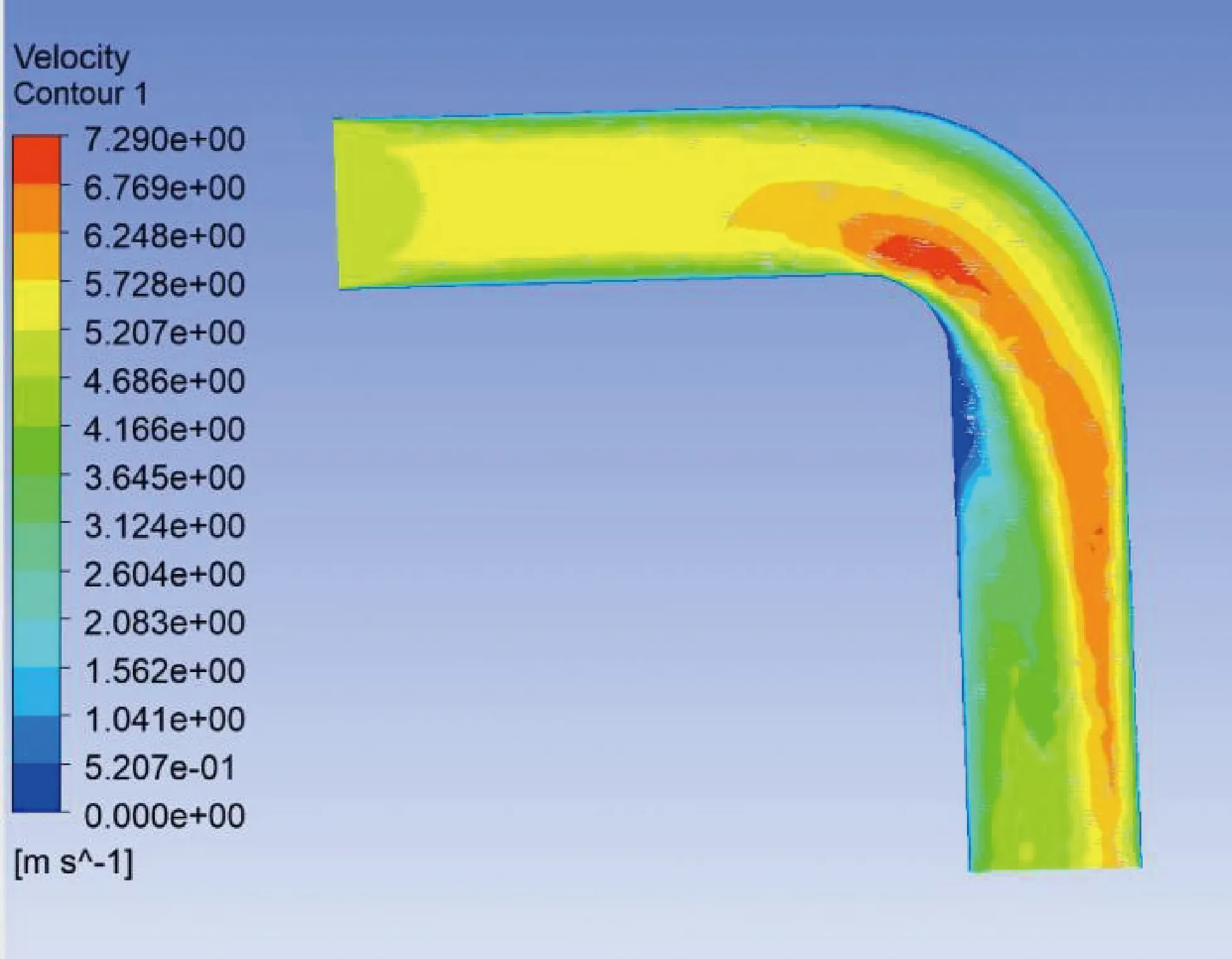
图5 流体速度分布
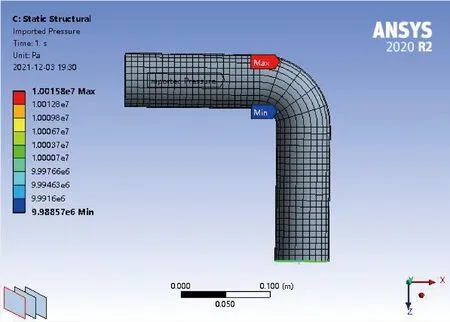
图6 流固耦合导入界面图
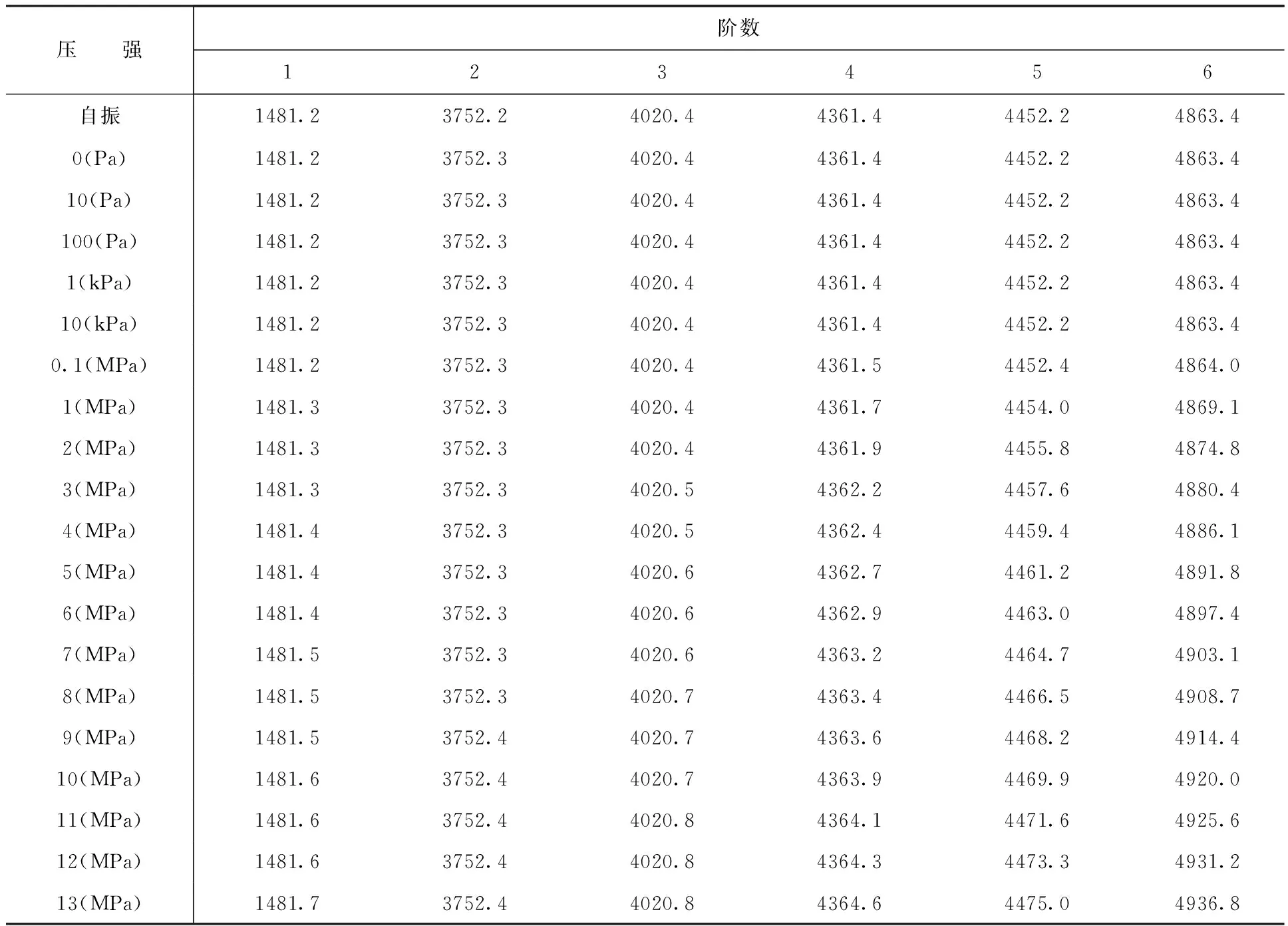
表2 不同压力条件下输油弯管的前六阶固有频率

续表

表3 不同流速条件下输油弯管的前六阶固有频率
下面是输油弯管在流速为5 m/s,压强为10 MPa 条件下,1至6阶振型图。

图7 输油弯管一阶振型图

图8 输油弯管二阶振型图

图9 输油弯管三阶振型图

图10 输油弯管四阶振型图
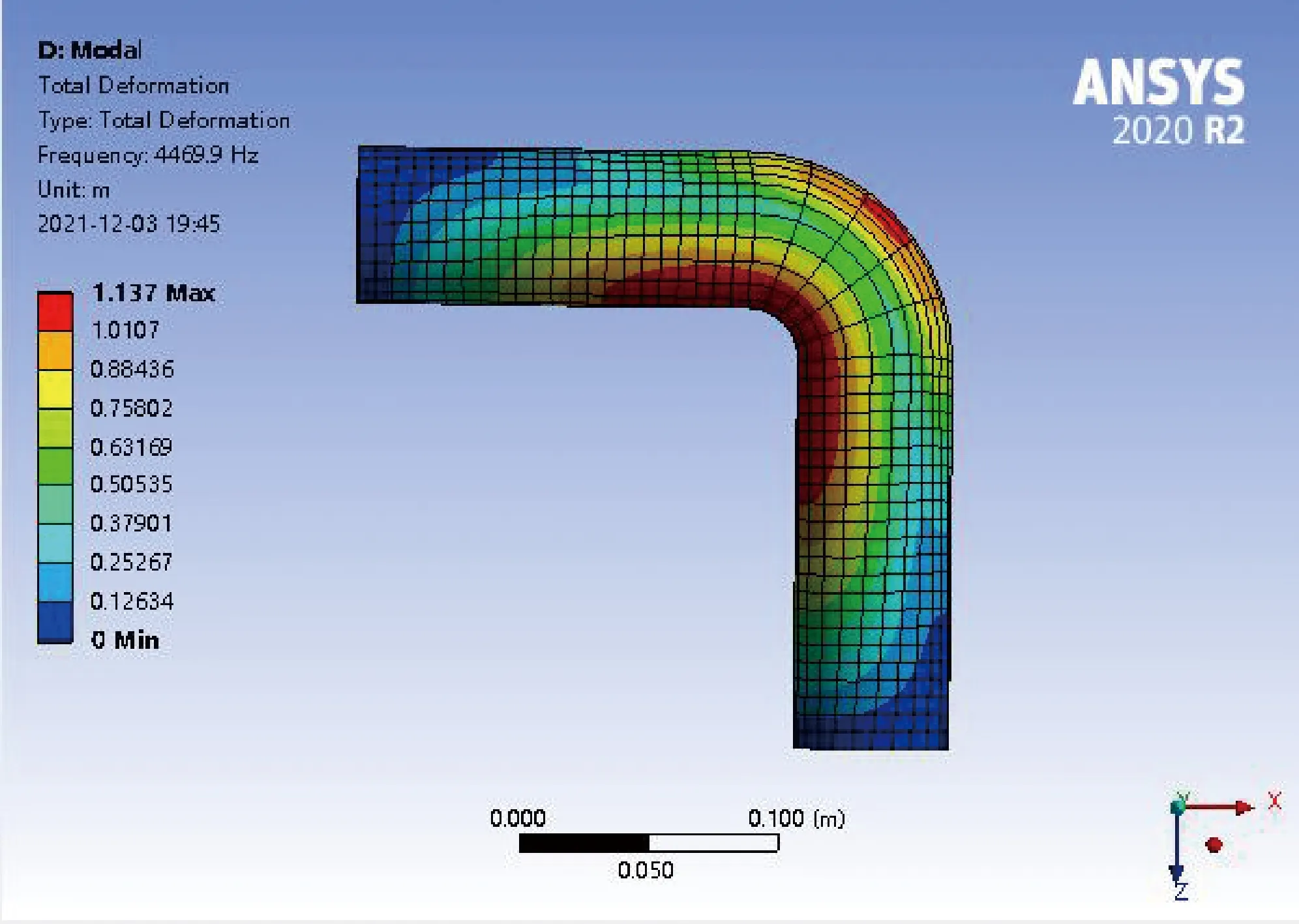
图11 输油弯管五阶振型图

图12 输油弯管六阶振型图
4 结论
(1) 研究表明:与输油弯管的自振频率相比,在压强和流速增大的情况下固有频率都会变大,对比流速和压强的情况,可以看出来流速对管道固有频率的影响比较小,而压强变化对管道固有频率的影响比较大。
(2) 这是因为流固耦合振动特性由流体内部的静压和动压共同作用引起的,只要超过管道的临界载荷才能够产生流固耦合,根据伯努利方程静压和动压之间是可以相互转化的,但是流速改变产生的动压转化成静压对管道壁的压力,远不如压强大小改变的作用明显。
