矿井通风网络解算研究现状与发展趋势

2021-04-22张景钢王清焱

华北科技学院学报 2021年6期

张景钢，何鑫，王清焱

(华北科技学院安全工程学院，北京东燕郊 065201)

0 引言

随着矿井开采深部不断加大，通风网络结构愈加复杂，通风问题越来越严重。因此矿井通风网络解算在通风管理中越来越重要。矿井通风网络解算是以通风网络图为基础，以矿井空气流动基本理论为依据，计算矿井巷道中的风量与风压。1928年波兰学者H.Czeczott提出了通风网络解算。此后，国内外学者进行了系统的研究，提出了很多通风网络解算方法和软件。现代通风管理主要是利用计算机技术对矿井通风网络进行解算。

故对矿井通风网络解算进行综述是非常必要的，本文在矿井通风网络解算方法的基础上阐述通风网络解算软件的研究现状。

1 通风网络解算研究现状

1.1 通风网络解算基础理论研究现状

矿井通风网络解算是以图论和通风基本理论为基础发展起来的。

瑞士数学家欧拉在1736年解决了柯尼斯堡七桥难题，从而开创了图论。英国格里斯在1852年提出四色问题，此后国外许多学者在二维平面内证明出了二着色图、三着色图、四着色图，这些证明推动了图论严密性的发展。英国数学家汉密尔顿在1859年提出在一张含有多个点的网络图中，经过图中每个结点刚好形成一次回路问题。

16世纪，人们开始把矿井进风和回风分开，并在矿井中尝试利用自然通风压力进行通风。18世纪俄罗斯著名科学家M.B罗莫诺索夫发表《关于矿井通风的理论》，初次系统阐述了空气在矿井巷道中流动的性质和规律。19世纪法国采矿工程师阿金森发表《关于矿井通风的理论》，提出的通风原理为现代通风设计奠定了基础。

1.2 通风网络解算三大定律研究现状

风网解算的理论基础是通风三大定律：通风阻力定律、节点风量平衡定律、回路风压平衡定律[1,2]。

(1) 通风阻力定律实质上是摩擦阻力定律和局部阻力定律的综合。在风阻一定的情况下，井巷通风总阻力与通过巷道风量的二次方成正比。

h=RQ2

(1)

对于一个具有n条分支的风网，每条分支的风量和通风阻力之间同样有一个确定的关系：

hj=Rj·|Qj|·Qj(j=1,2,…,n)

(2)

式中,hj为第j分支的通风阻力，Pa；Rj为第j分支的风阻，(N·s2)/m8；Qj为第j分支的风量，m3/s；n为风网中的分支数。

(2) 风量平衡定律是指在矿井风网中流入与流出任意节点的风流量Qi的代数和为零。

∑Qi=0

(3)

(3) 风压平衡定律是风网中每一分支始末两点之间的压力差等于该分支的通风阻力减去通风动力。当几条分支构成一个回路时，沿回路方向各分支阻力的代数和等于其动力代数和。

∑hi=Hf±Hn

(4)

式中，Hf为风机风压，Hn为自然风压。

1.3 通风网络解算方法研究现状

目前为止，矿井通风网络解算方法多种多样。分别是计算机技术普及前的图解法、物理模拟法和数学解析法。计算机技术普及后的回路风量法、割集风压法和节点风压法。如图 1所示。

图1 通风矿井网络解算方法

(1) 计算机技术普及前通风网络解算方法

图解法是指将通风网络中的各类参数标注在矿井坐标图上，以风路串联、并联以及通风的三大规律为依据，按照一定的步骤，求解通风网络的各类参数[2]。1964年我国通风专家唐海青在《矿井通风网络的动坐标解法及其应用》中提出动坐标解法，以静态图解法为基础，通过坐标的移动，求解通风网络的各类参数。1975年我国著名学者宋化沂在《矿井通风网络解法(上)——逐孔图解法》一文中，提出了利用网孔图求解通风参数[3]。虽然随着计算机技术的迅速发展，但是该方法矿井通风管理中仍然适用。

物理模拟法是指采用液体网络或电气网络去模拟通风网络[4]。由于液体网络的构建成本高，故一般使用电气网络进行模拟通风网络。但是国内外学者通过大量实验得出，采用水管网络进行通风网络模拟更为准确。物理模拟法作为矿井通风的一种过渡方法，随着计算机技术的发展，逐渐被淘汰。

数学解析法是国内外学者研究最多，使用最为广泛的方法。数学解析法是以矿井通风网络的各项参数为未知量，以通风三大定律为基础理论，建立方程组进行求解。常用的方法有斜量法、迭代法、直接代入法。

(2) 计算机技术普及后通风网络解算方法

计算机作为矿井通风网络解算的重要工具。在计算机技术普及后，国内外学者利用计算机技术对回路风量法、割集风压法和节点风压法[4]进行了研究。

回路风量法是以通风三大定律为理论基础，以回路矩阵为工具，求解回路风量。此法利用通风三大定律中的风量平衡定律和回路矩阵得出分支风量方程，运用回路风压平衡方程和回路矩阵，经过计算得出M-N+1个方程(即M-N+1个回路风量)，联立方程组求解回路风量及其他参数。

割集风压法是一种假想的风压，假设每个基本割集中各分支都有一定的风压，因树枝只出现在一个基本割集中，所以树枝的分压就等于它对应的割集分压，而余下分支的风压等于它所在的几个割集的割集风压的代数和。根据这种关系可由风流流动基本规律建立以基本割集的风压为未知量的非线性方程组，求解出割集风压。

节点风压法是以各分支风压之间的关系为依据，并以通风三大定律为理论基础，求解通风网络中任一节点风压。此法中，将各分支分压之间的关系和通风三大定律中的风压平衡定律联立方程组，使用泰勒公式展开并采用牛顿迭代法求解节点风压。

回路风量法在风网解算方法中具有非常重要的地位，所以在计算机技术普及前后时期的风网电算方法均采用此法。

1.4 通风网络解算数学模型研究现状

经过国内外学者多年的研究，现有的通风网络解算数学模型包括回路法数学模型、节点风压法数学模型和割集法数学模型[5]。

(1) 一个通风网络包括u个节点，v个分支，其任一颗生成树与其余树枝可组成u-v+1个独立回路。以空气能量守恒定律为依据，利用基本回路矩阵C，可使u-v+1个独立回路组成u-v+1个非线性方程。再以空气质量守恒定律为依据，利用基本回路矩阵和基本关联矩阵之间的关系，可使u-v+1个独立回路风量表示u个分支风量。从而推导出回路法数学模型：

(5)

Q=CTQy

(6)

式中，i=u-v+1；Rj为分支j的风阻；Qj为分支j的风量；hfi为节点i的风机风压；hNj为第j条回路的自然风压；CT为基本回路矩阵的转置矩阵；Qy为余树枝风量。

(2) 一个具有a个节点，b个分支的通风网络，假设a-1个节点的风压是单独存在的，则通风网络中的b个分支的风压向量U=(u1,u2,u3,…,un)是基本关联矩阵B的转置矩阵BT与a-1个节点的分支风压向量S=(s1,s2,s3,…,sa-1)的乘积。可使用基本关联矩阵B与b个分支的风量T=(t1,t2,t3,…,tb)的乘积等于零来表示风压平衡定律。再把利用伯努利方程推导得到的分支的风阻hk=Si-Sj±hf(hf为通风机风压)代入到通风阻力定律。从而推导出节点风压法数学模型：

U=SBT

(7)

BT=0

(8)

(9)

(3) 一个具有a个节点，b个分支的通风网络，其任一颗生成树皆有a-1个树枝，可组成(a-1)·b的基本割集矩阵M，基本割集矩阵M的转置矩阵MT与其树枝分压的向量Ns=(n1,n2,n3,…na-1)T的乘积为分支风压向量N=(n1,n2,n3,…nb)T。以风量平衡定律为依据，使基本割集矩阵M与风量向量Q=(q1,q2,q3,…qb)T的乘积为零。从而推导出割集法数学模型：

N=MTNs

(10)

(11)

1.5 基于回路风量法的斯考德-恒斯雷法的算法的修正

在矿井通风网络解算的发展过程中，国内外学者研究出了不同的解算方法，如斯考德-恒斯雷(Scott-Hinsley)法，牛顿-拉夫森法，京大一试法，京大二试法等。其中以回路风量法为基础的斯考德-恒斯雷法使用广泛。本文以回路风量法基本原理为基础对斯考德-恒斯雷法的算法原理和基本思路进行阐述，并对此法的修正进行推导。

(1) 回路风量法基本原理

回路风量法是矿井通风网络数值法中最早采用的方法。该法是将通风阻力定律、风量平衡定律、风压平衡定律建立方程组求解回路风量及其他参数。这三个基本定律可描述为：

(12)

qj=∑Csj·qys(j=1,2,…,n)

(13)

(14)

式中，b为风网的独立回路数，b=n-m+1；hfj为通风机风压，描述为风机所在分支风量的函数，即hfj=f(qj)；hNj为自然风压，一般处理为常数；qj为第j分支风量，j=1,2,3…,n；qys为余数弦风量；Cij为独立回路矩阵。

当分支的风阻与风机风压已知时，将以上三式联立方程组有(2n+b)个未知量，与方程个数相同，因而有定解。将式(12)代入式(14)中得：

(15)

再将式(13)代入式(15)得：

(16)

在求回路风量Qy后，将其代入式(13)便可求出分支风量Qj，再将Qj代入式(12)中又可求得分支通风阻力hj。

(2) 斯考德-恒斯雷法

斯考德-恒斯雷法是由英国学者斯考德和恒斯雷对美国学者哈蒂·克劳斯提出的用于水管网的逐次计算法进行改进并用于风网解算。

① 斯考德-恒斯雷算法原理

对节点数为m、分支数为n的通风网络，选定一组余树弦风量为独立回路风量，记为qy1，qy2，…qyb,b=n-m+1。以qy为变量，由各个独立回路风压平衡方程式(16)可得非线性方程组：

(17)

式中，Rj为分支风阻；qj为分支风量；qy1,qy2…,qyn为余数弦风量；式中有b个方程，含有b个未知数(qy1，qy2,…,qyb)，表示方程组有定解。

② 斯考德—恒斯雷法的修正

设风网风压方程组式(17)进行k次迭代后，得到第k次风量近似值：

(18)

利用泰勒级数展开式将(9)式展开：

(19)

将式(19)内省略二次以上高阶微量，式(19)的第k+1次线性化近似式为：

(20)

写成矩阵形式：

(21)

为简化计算，对式(21)做出以下假定：

(22)

即式(21)系数矩阵具有主对角线优势。若省略非对角线上的各项，则可变为：

(23)

式(23)可写为：

(24)

③ 斯考德—恒斯雷法存在的问题与改进

在使用斯考德—恒斯雷法计算的过程中，因拟定的初始风量值可能与真实值相差较大，使得计算结果不准确。斯考德—恒斯雷法忽略泰勒级数展开式中的高阶微量与Jacobi矩阵中的同阶微量，使公式推导不严密。

因此，为使斯考德—恒斯雷法能够精确解算，首先使拟定的初始风量值尽可能地接近风量真实值，其次使Jacobi矩阵中的主对角元素远远大于次对角元素。为使斯考德—恒斯雷法更加完善，国内外学者提出了利用改进的BFS法求最小生成树、用双通路法圈化回路[6]和基于信赖域的方法[7]进行网络解算。通过应用证明，改进后的斯考德—恒斯雷法能更加准确的解算出所要求的风量值。

2 通风网络解算软件研究现状

2.1 通风网络解算软件数据库设计

目前大多数煤矿在记录和处理矿井通风数据多采用Excel[8]。因Excel电子表格中的数据能与Access数据库实现互导。故以Access数据库为底层开发的通风网络解算软件能够有效的管理通风数据[9]。通风系统数据库包括巷道编号、通风网络各分支始末节点、巷道名称、断面面积、巷道风阻、固定风量、自然风压、分支标识等主要通风网络参数(见表 1)。

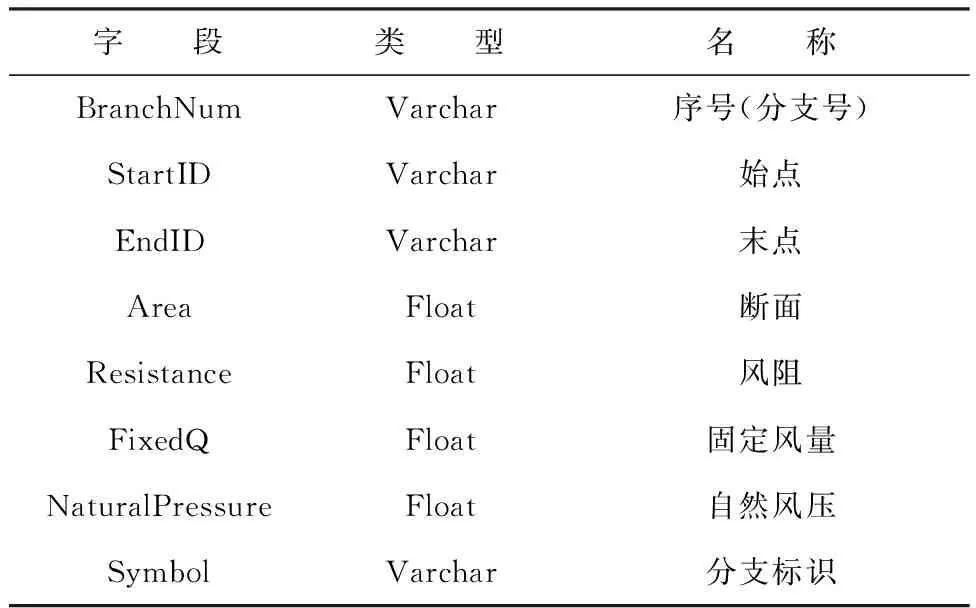
表1 通风网络参数表

2.2 通风网络解算软件功能实现

通过阅读国内外有关通风网络解算软件的文献发现，解算软件的主要功能模块包括数据处理模块、风量调节模块、网络解算模块等[10]。

(1) 数据处理模块

数据处理模块作为风网解算的第一步，主要包括通风数据处理与维护和图形数据更新与修改等功能。通风数据的处理与维护是对矿井通风巷道各分支节点数据、风机各项参数等数据进行增加、删除、更新处理。

(2) 网络解算模块

网络解算作为通风网络解算软件的核心功能，将数据处理模块提供的原始通风数据为基本未知量，以斯考德-恒斯雷算法或牛顿-拉夫森法为数学模型，使用Visual Basic或VB.Net等编程语言，采用迭代计算方法，设置迭代次数和迭代精度，进行网络解算，最终解算出矿井通风网络各项参数的近似值，如图2所示。

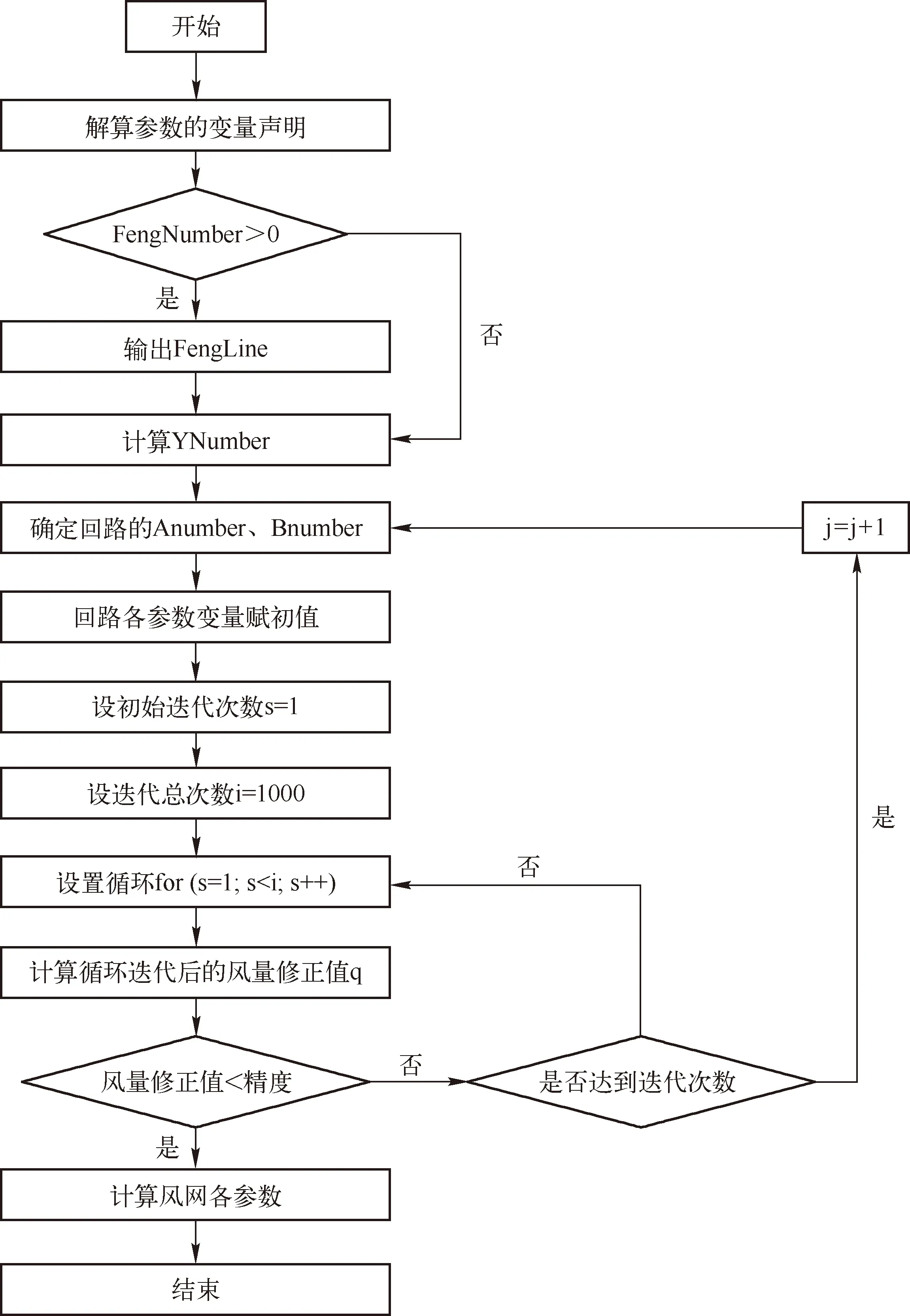
图2 网络解算流程

网络解算软件在进行解算时，首先要对各解算参数进行变量声明。然后再判断是否有风机，在有风机的情况下，进行风机曲线拟合计算机，计算出回路中的节点数和分支数，确定回路。给回路上的各参数变量赋初值，并设置迭代次数，若迭代计算后的风量修正值大于预定精度，则要重新迭代，依此反复，直到其小于预定精度为止。最终，计算出风网中的其他各参数。在图2中，变量FengNumber为风机数，变量FengLine为风机曲线，变量ANumber为回路中的节点数，变量BNumber为回路中的分支数。

(3) 风量调节模块

风量调节模块的主要功能是对矿井通风网络中的风量进行调节，其自然分风调节法和固定调节法在矿井通风网络风量调节中具有非常重要的作用。

① 自然分风调节法

② 固定风量调节法

通风网络中任意选一个回路,该回路含固定风量分支,计算回路中除固定风量分支以外的其他分支风阻：

将RG与现有风阻值RX进行比较,若RG=RX，该分支不调节；若RGRX，该分支需增阻调节。

2.3 通风网络解算软件研究方向

通风网络解算软件应用最广泛的有日本的井上雅弘编制的风丸软件、美国密歇根技术大学开发的Mfire程序与安徽理工大学开发的MVENT等，这些软件均是围绕可视化进行研究的。

国内外学者开发通风网络解算软件的方式有：①以AutoCAD的二次开发系统为底层进行开发；②使用面向对象的高级编程语言进行开发。③使用地理信息系统的二次开发功能进行开发。

(1) Auto CAD二次开发

使用Auto CAD的二次开发功能进行开发网络解算软件，以实现CAD绘制的矿井通风网络图进行通风模拟解算。Auto CAD的二次开发有Auto LISP、Visual LISP等方式。此方法优势在于矿井通风网络图和通风模拟解算是在同一开发环境进行的，使用方便；不足在于Auto CAD 二次开发的兼容问题，会出现调用不协调等问题。

(2) 使用编程语言开发软件

编程语言开发的通风网络解算软件可以在单独的环境中运行的。该方式开发的通风网络解算软件在使用时，导入的电子矿图格式要与软件绘制而成的电子矿图的格式相同。具有有较强的灵活性，并且容易修改成其他系统，但开发难度较大。

(3) 地理信息系统

地理信息系统是以地理数据为依据，以计算机的软硬件为载体，对空间信息进行研究和管理的系统[11]。以地理信息系统为底层开发的通风网络解算软件在使用时必须将Auto CAD绘制的矿井通风网络图导入该系统中。该系统在编辑电子矿井通风网络图方面较弱，编辑后的电子矿井图存在兼容性问题。

3 通风网络解算软件存在的不足与展望

3.1 通风网络解算软件存在的不足

经过国内外学者多年的研究，通风网络理论、网络解算方法已趋于成熟。但在网络解算软件的开发方面，却存在着不足。

(1) 国内外学者采用高级编程语言开发的网络解算软件，仅仅能在Windows操作视窗中使用，在Linux，Macos与一些物联网系统中无法使用。

(2) 在现有的网络解算软件中，各解算软件数据不互通、更新不及时，解算结果与实际风量相差较大，从而无法精确反应井下的实际情况[12,13]。

(3) 现有软件操作过于复杂，界面不美观，智能化程度都相对较低[14]。

3.2 通风网络解算模型展望

基于风量超前计算模型的研究。由于矿井的不同用风点环境之间有较大差异，各用风点的风量不同，致使解算结果与实际风量相差较大。为使解算结果更加准确，需要风量超前计算模型得出的风量作为参照标准，将通风网络解算模型得出的风量与之对比，减少与实际风量之间的差异。对基于风量超前计算模型的研究是未来的发展趋势。

3.3 通风网络解算软件展望

(1) 通风网络解算软件的跨平台。为了能让网络解算软件在不同的操作视窗中使用，将云服务与浏览器扩展程序技术结合，矿井数据实时上传至服务器，服务器通过强大算力快速得出结果，个人通过访问浏览器扩展程序了解情况，解决多平台使用的问题。对通风网络解算软件跨平台的研究是未来的发展趋势。

(2) 通风网络解算软件的智能化[15,16]。随着数据库技术、编程语言的逐渐成熟完善，为矿井通风软件的智能化奠定了坚实基础。通风网络解算软件的智能化实质上是以当前流行的大数据、云计算等先进技术为基础开发的智能化软件，远程操控瓦斯、风速、风压传感器，实现智能监测、控制、计算等操作。风网解算软件的智能化具有计算精度高、省时省力等特点。对通风网络解算软件智能化的研究也是未来的发展趋势。

(3) 通风网络解算软件研究方向的多元化。目前大多都是基于可视化进行研究，太过单一，难以保证解算结果的准确性。