颗粒间摩擦对颗粒流润滑影响的力学机制

孟凡净，刘华博，花少震

(河南工学院机械工程学院，新乡 453003)

颗粒流润滑是最新被研究者关注的工程润滑问题[1-4]。在极端的制造环境下，例如热锻、热压铸、航空航天等，传统的润滑剂可能无法有效地润滑零件，甚至由于高温、高压和高真空而失去润滑性能。然而，颗粒流润滑非常适合这种极端工况环境下的工程润滑问题，原因是由于固体颗粒具有较强的耗散性和对高温不敏感的特点[5-10]，因此该润滑方式环境适应性较强，可以不受润滑工作过程中高温、高压和高真空环境的影响[11-15]。作者的前期研究结果表明：把坚硬、干燥和无黏性的微米级颗粒导入摩擦副间隙用作润滑剂，可以减小摩擦副的摩擦和磨损，从而起到保护摩擦副表面的目的[1,2,15]。

与传统的流体动力学润滑理论相比较，把固体颗粒填充到摩擦副间隙中，在动摩擦副驱动下形成颗粒流润滑时，在应力-应变关系、速度适应机制、摩擦学与承载特性和微观力学机制等方面两者既有一定的相似之处又有本质上的不同[16]。在微观尺度上需要研究颗粒间滑动和接触的力学行为，在宏观尺度上需要研究速度与波动的力学特性以及摩擦学力学机制等。目前，颗粒流润滑力学理论研究还处于起步阶段，虽然国内外学者通过开展相关研究，取得了一些有益的结果[17-19]，但仍有许多问题亟待解决，其中颗粒间摩擦对颗粒流润滑影响的力学机制就是其中的关键科学问题之一。针对该问题开展系统研究，可以掌握颗粒间摩擦对颗粒流润滑状态下的摩擦力学机制和宏微观特性的影响规律，而该规律和特性可以为颗粒流润滑滑动轴承的设计和参数选择提供理论指导。

颗粒润滑介质本身是散体，它非连续、非均匀和各向异性等特点导致连续性假设不成立，当颗粒润滑介质在上、下摩擦副间做剪切运动时，颗粒润滑介质的流动特性：一方面可以表现出与固体流动类似的特性；另一方面也可以表现出与液体流动相似的特性。此时，颗粒流润滑系统显示出许多独特的力学特性，为现有的力学理论所不能描述，这是由于颗粒润滑介质沿空间和随时间分布以及颗粒润滑介质间接触强度各异所导致的必然结果[20-23]。颗粒润滑介质间相互作用的各向异性特性不仅与颗粒体的大小、形状、性能参数等密切相关，而且又受诸多外部和边界控制条件的影响，比如载荷、剪切速度以及界面粗糙度等。正是由于该原因，所以颗粒流润滑系统的接触特性和动力学性能非常复杂，系统的应力-应变关系也非常复杂，同时由应力诱发的颗粒润滑介质间相互作用关系的演变也具有明显的不确定性[24-26]。

基于颗粒流润滑系统的离散性和复杂性，无法用传统的连续性介质力学的方法来进行研究，通过参阅相关文献表明，Cundall 等[27]首先提出的离散单元法是解决此类散体系统的有效方法。本文为了研究颗粒间摩擦对颗粒流润滑状态下的摩擦力学机制和宏、微观特性的影响规律，采用离散单元法理论建立了颗粒流润滑系统的数值分析模型，并利用该模型对颗粒间摩擦对颗粒流润滑影响的力学机制进行了详细的分析和研究。

1 颗粒流润滑模型和理论

1.1 颗粒流润滑模型

在本文研究中，采用的摩擦副为平形滑动摩擦副，该摩擦副为一种典型摩擦副类型。对平行滑动颗粒流润滑进行分析，不但可以有助于理解颗粒流润滑的基本减摩机理和润滑特征，也可以为设计颗粒流润滑滑动轴承提供最基本的设计理论基础。如图1 所示，上摩擦副是由50 个直径大小为34 μm 的球形颗粒组成，所有的球形颗粒连成一体，并且所有球形颗粒具有相同的y 坐标，对上摩擦副施加x 向和转动约束，同时允许上摩擦副沿坐标轴y 向自由移动，在此基础上，在上摩擦副上面施加压力载荷P。下摩擦副是由一线性墙体构成的，并且下摩擦副可以以速度U 沿坐标轴x 向做剪切运动。上、下摩擦副之间的颗粒润滑介质的数量为1200 个球形颗粒，其直径大小范围为27 μm～41 μm 且服从均匀性分布特性，所有的颗粒润滑介质均匀地散布在1.7 mm×0.85 mm 的矩形空间中，矩形空间的长度方向定义为x 向，宽度方向定义为y 向。在颗粒流润滑离散元模型的左、右边添加周期性边界条件，这样可以使得颗粒从边界的一边出来后能以相同的高度和速度在边界的另一方出现。图1 中的网状结构为颗粒流润滑离散元模型达到初压平衡状态时，颗粒润滑介质之间的接触力网络结构，简称力链网络。力链网络中的网状线条越粗，说明颗粒润滑介质之间的接触力越大，则颗粒润滑介质的承载能力越强，反之，则越弱。这说明，采用固体颗粒润滑介质来进行滑动轴承润滑，这些固体颗粒润滑介质不但可以起到减摩润滑的效果，而且还具有接触承载的特性，而接触承载特性则是油润滑介质所不具备的。

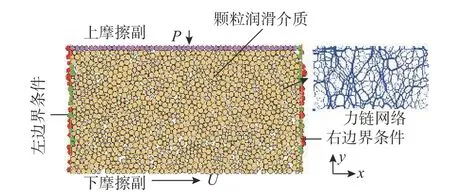
图 1 颗粒流润滑离散元模型Fig.1 Discrete element model of granular flow lubrication

1.2 颗粒流润滑理论

颗粒润滑介质是离散的，因此不满足连续性假设条件，采用传统的连续力学理论很难对颗粒流润滑系统进行研究和分析。离散单元法在解决离散颗粒物质系统方面具有编程简单、计算精度高和效率快的优势，因此特别适合用该方法对该颗粒流润滑系统进行研究[8，28-30，31]。

对于该颗粒流润滑系统，颗粒润滑介质之间是互相接触的，并且应用力-位移定律来对该系统进行分析。根据静力学受力平衡的原理，在没有外部条件或外力施加的初始时刻，颗粒润滑介质之间是非连续的颗粒体集合，并且所有的颗粒润滑介质都是处于力平衡的初始状态。接下来，当外部条件(如剪切速度、振动等)或外力作用在该颗粒流润滑系统时，部分颗粒体会产生加速度并发生位移，在此情况下这些发生位移的颗粒体的空间位置也随之发生改变，进而形成新的力学体系。

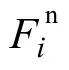
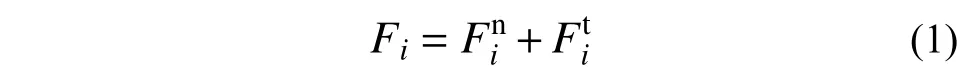
式中，i(i=1,2,3)表示空间坐标轴的3 个方向。

法向接触力可以表示为：

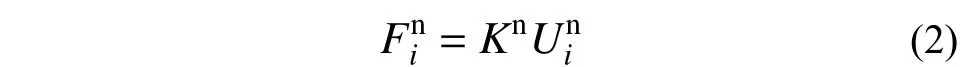
切向接触力可以通过增量形式进行计算，在初始接触处，切向接触力初始化为零，Δt 时间后的切向接触力增量可以表示为：

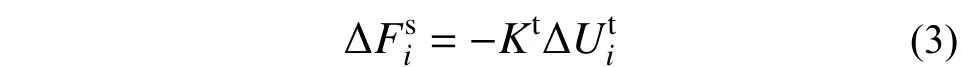
如式(4)所示，新的切向接触力等于老的切向接触力及接触力增量之和：

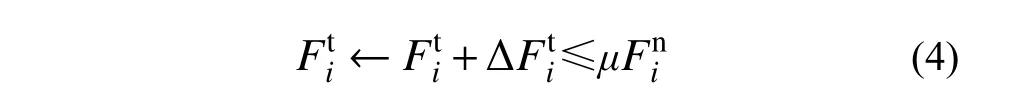
式中，μ为颗粒体间摩擦因数。

Hertz-Mindlin 接触模型是研究球形颗粒接触中所采用的一种非线性接触模型，在本文颗粒流润滑离散元数值模型建立过程中，所采用的接触模型为该模型。Hertz-Mindlin 接触模型的定义主要依赖于两个参数，一个为切变刚度G，另外一个为泊松比ν。在该颗粒流润滑离散元数值模型中，当接触的对象为两个颗粒体时，弹性属性定义为两个颗粒体弹性属性的平均值；当接触的对象为颗粒体和墙体时，墙体考虑为刚性的，因此弹性属性定义为颗粒的弹性属性。因此，法向和切向接触刚度的计算公式为[32]：

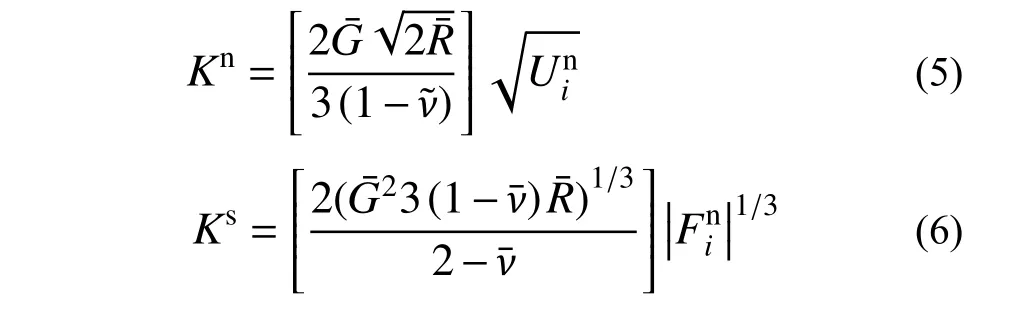
1.3 离散元数值计算流程

在颗粒流润滑离散元数值编程和计算过程中，所采用的数值算法为动态显式算法。与动态隐式算法相比较并根据通用的数值分析理论可知，该算法的程序编制较为容易，同时该算法的差分求解过程无需平衡迭代，因此求解速度快、计算简单。

在数值模拟计算之前，首先在上摩擦副上面施加沿坐标轴y 向的恒定压力载荷P，颗粒润滑介质集合在重力和压力载荷的共同作用下达到初始化平衡状态，之后，在下摩擦副上施加沿坐标轴x 向的恒定剪切速度U，随之，下摩擦副把运动和力依次传递给颗粒润滑介质和上摩擦副。与传统的固体润滑膜不同，颗粒润滑介质随机分布在上、下摩擦副之间并且颗粒润滑介质之间没有任何的粘结。如图2 所示，此为详细的颗粒流润滑离散元数值计算流程。

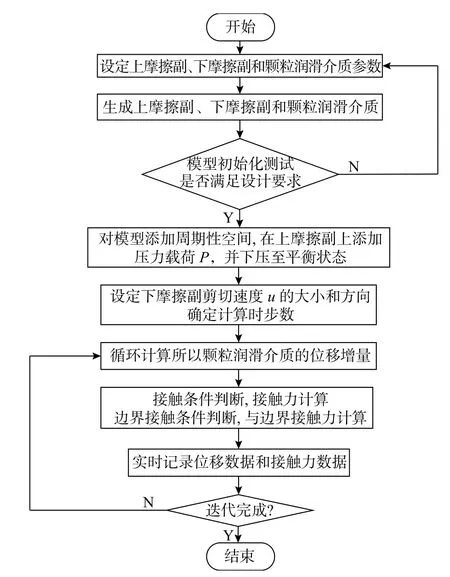
图 2 计算流程图Fig.2 Numerical calculation flow chart

如图1 所示，颗粒润滑介质的材料选择为碳化硅，上、下摩擦副的材料分别选择为合金钢(1Cr18Ni9Ti)和45#钢。在选择颗粒润滑介质、上摩擦副和下摩擦副的材料属性的时候，需要对建立的颗粒流润滑离散元数值模型进行反复的初始化测试，以最终确定合适的材料配比属性。颗粒流润滑离散元数值模拟过程中，详细的参数为：上摩擦副的材料密度为7900 kg/m3，材料的泊松比为0.3，弹性模量为2.06×1011Pa，摩擦系数选择为0.2；下摩擦副法向、切向刚度为1.0×1010，摩擦系数为0.5；颗粒润滑介质弹性模量为2.2×1011Pa，密度为3210 kg/m3，泊松比为0.142；施加在上摩擦副上的压力载荷为2.5 MPa；下摩擦副的剪切速度为5 m/s。上、下摩擦副和颗粒润滑介质的材料，以及上、下摩擦副摩擦系数的选择都是基于对颗粒流润滑离散元模型反复的初始化试验确定的。

2 结果及讨论

2.1 颗粒间摩擦对颗粒流润滑影响的摩擦力学机制

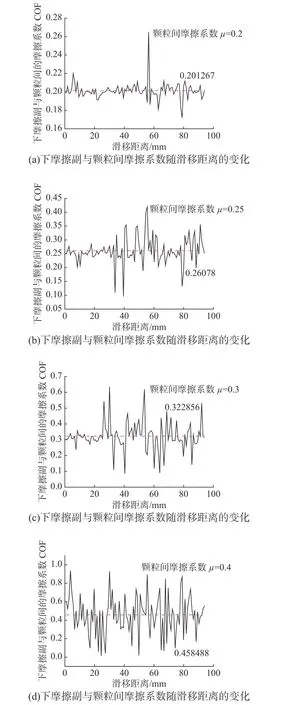
图 3 下摩擦副和颗粒间的摩擦系数COF随滑移距离的变化规律Fig.3 The variation of friction coefficient between the lower friction pair and the granules with the slip distance

颗粒间摩擦的大小会改变颗粒润滑介质之间的流动和接触特性，并会对颗粒润滑介质之间的受力产生影响，从而影响颗粒流润滑系统的摩擦力学机制。为了对此进行研究，分析了下摩擦副和颗粒润滑介质之间的摩擦系数(COF)在不同颗粒间摩擦系数下的变化规律，如图3 所示。研究过程中，颗粒间摩擦系数μ的取值范围为0.2～0.4，该取值范围是根据颗粒流润滑离散元模型的反复初始化调试并结合端面摩擦学试验的基础上来综合确定的。当颗粒流润滑离散元模型中的颗粒间摩擦系数取为μ=0.15(小于0.2)时，试验中在上摩擦副上面施加压力载荷P 的状况下，部分颗粒润滑介质会超出下摩擦副的y 向边界，使得系统无法达到初压平衡状态。针对该实际情况，采用RTEC 端面摩擦试验机开展了验证性的试验，试验过程中的上、下摩擦副材料属性与颗粒流润滑离散元模型一致，由于在市场上无法购买到合适的碳化硅颗粒，因此用颗粒间摩擦系数接近于0.15 的微钢球进行了代替。试验结果表明：当在上摩擦副上施加压力载荷时，由于微钢球的表面比较光滑，上、下摩擦副之间的微钢球颗粒很难形成有效接触，会出现一旦施加压力载荷，微钢球所形成的颗粒体就会崩塌的现象，从而导致颗粒流润滑系统无法达到初始化平衡状态。另一种情况，当颗粒流润滑离散元模型中的颗粒间摩擦系数取为μ=0.5(大于0.4)时，颗粒流润滑系统在施加压力载荷P 的状况下可以达到初始化平衡状态。但是，当下摩擦副做剪切运动时，上、下摩擦副之间的颗粒润滑介质会出现内部阻塞并导致离散元运算终止的现象。针对该情况，同样采用RTEC 端面摩擦试验机开展了针对性的验证试验，试验过程中为了接近离散元计算中的颗粒间摩擦系数，所有的微钢球统一在其表面用强力胶粘接了一层铁粉。试验结果表明，当下摩擦副做剪切运动时，由于微钢球之间的摩擦力过大，部分微钢球之间极易形成一团，并阻碍其余微钢球的正常流动，从而导致整个颗粒流润滑系统阻塞现象的产生。

如图3 所示，下摩擦副和颗粒润滑介质之间的摩擦系数(COF)随着滑动距离的增大而波动变化，平均摩擦系数[COF]在颗粒间摩擦系数μ=0.2、0.25、0.3、0.4 时分别为0.201267、0.26078、0.322856 和0.458488 。为了进一步分析颗粒间摩擦系数对平均摩擦系数的影响效果，分析了平均摩擦系数[COF]随颗粒间摩擦系数的变化规律，如图4 所示。从图4 可以看出，[COF]随着颗粒间摩擦系数的增大而增大，且服从形如公式[COF]=a+b×μ所示的线性变化趋势，系数a、b 的数值分别为-0.064、1.309，拟合精度为0.99679。

以上研究结果表明，颗粒间摩擦对颗粒流润滑系统的减摩润滑特性具有显著影响，选取具有合适颗粒间摩擦的颗粒润滑介质尤为重要。当颗粒间摩擦不满足颗粒流润滑系统要求时，会增大颗粒流润滑系统的摩擦达不到减摩润滑效果，或者出现颗粒润滑介质流动不畅造成阻塞现象产生，甚至会导致颗粒流润滑系统无法达到初压平衡状态等。基于此，在颗粒流润滑滑动轴承的设计过程中，需要反复调试摩擦副间颗粒润滑介质的表面特性，从而选择具有合适颗粒间摩擦并能够有效起到减摩润滑效果的颗粒润滑介质。

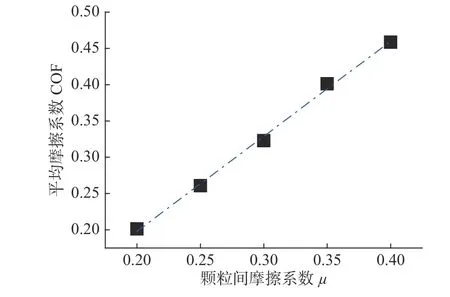
图 4 平均摩擦系数COF 随颗粒间摩擦的变化规律Fig.4 The variation of the average friction coefficient with the inter-particle friction coefficient

2.2 颗粒间摩擦对颗粒流润滑系统的微观影响

当颗粒润滑介质之间的摩擦改变时，系统内颗粒体间的微观力学性能也必然会发生改变。为了对此进行研究，分析了颗粒流润滑系统的配位数CN 和滑动率Sl 在颗粒间摩擦系数μ=0.2、0.25、0.3、0.4 时的变化规律，如图5、图6 和图7 所示。

如图1 所示，在颗粒流润滑系统内部，颗粒润滑介质之间是互相接触的，该接触特性是以力链网络的形式来呈现的，并通过该力链网络来传递系统内部的作用力。加载引起的微观组织演变可以用接触法向、分支矢量和配位数CN 来进行表征。颗粒流润滑系统中的配位数CN，定义为颗粒的平均接触数目。配位数是反映颗粒润滑介质之间接触紧密程度的关键性微观力学参数。当颗粒润滑介质之间的接触程度较为紧密时，配位数较大，反之，当颗粒润滑介质之间的接触程度较为疏松时，则配位数较小。

如图5 所示，平均配位数在颗粒间摩擦系数μ=0.2、0.25、0.3、0.4 时分别为2.87、2.52、2.2和1.92。这说明较小的颗粒间摩擦系数会使得颗粒流润滑系统内产生相对较大的配位数，然而当颗粒间的摩擦系数较大时，颗粒润滑介质会通过颗粒间滑动和滚动的形式重新调整位置并产生相对较大的配位数。以上研究结果表明，颗粒流润滑系统内的配位数会随着颗粒间摩擦系数的减小而增大。当颗粒间的摩擦系数减小时，颗粒间的剪切运动被抑制从而使得颗粒润滑介质之间的接触变得较为紧密，而颗粒润滑介质之间的接触紧密程度可以用固体体积分数来进行衡量，其中固体体积分数表示颗粒润滑介质实体所占的体积百分比，如图6 所示。从图6 可以看出，颗粒流润滑系统的固体体积分数随着颗粒间摩擦系数的增大而减小，也就是说颗粒间的摩擦系数越小，则颗粒流润滑系统的固体体积分数越大，而固体体积分数增大则意味着颗粒润滑介质之间的接触则越紧密。

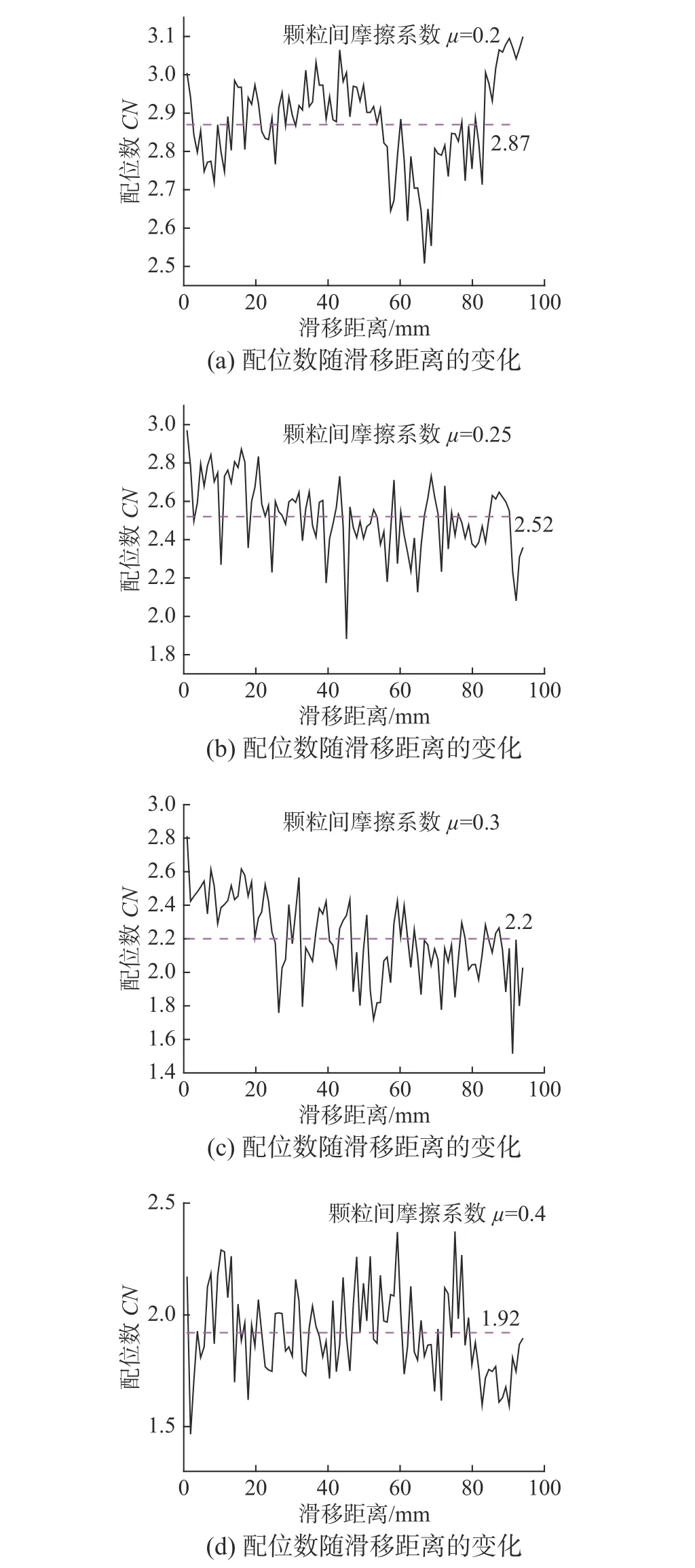
图 5 颗粒流润滑系统内的配位数CN随滑移距离的变化规律Fig.5 Variation of coordination number with slip distance in the granular flow lubrication system

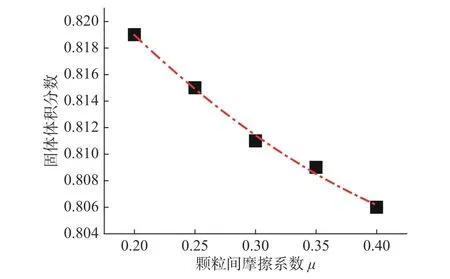
图 6 固体体积分数随颗粒间摩擦系数的变化规律Fig.6 Variation of solid volume fraction with inter-particle coefficient

颗粒流润滑系统的滑动率Sl，定义为滑动接触与总接触的比率，以及所有颗粒的累积平均转动，分别被用来量化颗粒的滑动和滚动。根据Suiker 等[33]的研究，滑动被认为是发生在切向接触力等于总切向接触力的接触点处，并且总的切向接触力是由法向接触力和颗粒间摩擦角决定的，同时遵循库仑摩擦定律。如图7 所示，颗粒流润滑系统的滑动率与颗粒间摩擦系数的大小密切相关，并且颗粒间摩擦系数越小则颗粒流润滑系统的滑动率越高。当颗粒间摩擦系数μ从0.4、0.3 下降为0.25、0.2 时，颗粒流润滑系统的平均滑动率反而从1.15%、1.59%增长为2.12%和3.93%。颗粒润滑介质之间的接触形式主要是滚动接触，同时伴随着少量颗粒润滑介质之间的滑动接触形式的存在。具体原因可能是由于，当颗粒间摩擦系数变小时，颗粒润滑介质之间的接触会变得紧密(如图6 所示)，紧密的颗粒间接触会抑制部分颗粒之间的相对滚动，而这部分颗粒润滑介质的空间位置要发生变化则会转化为滑动接触的形式来实现。颗粒流润滑系统中滑动率随颗粒间摩擦系数的变化规律与颗粒物质双轴压制系统类似[34]。在颗粒物质双轴压制系统中，颗粒物质间的滑动率同样会随着颗粒间摩擦的减小而增大，而该特性与本研究中的剪切颗粒流润滑系统具有一致性。

2.3 颗粒间摩擦对颗粒流润滑系统的宏观影响

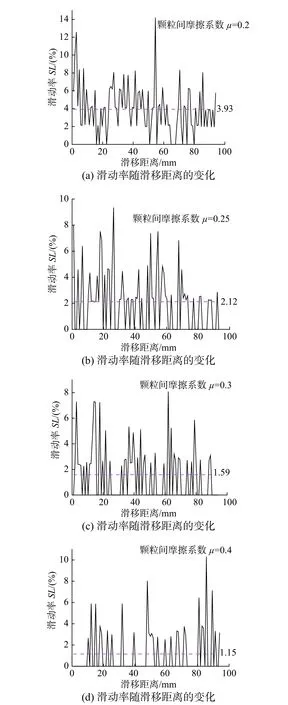
图 7 颗粒流润滑系统内的滑动率SL随滑移距离的变化规律Fig.7 Variation of the sliding fraction with slip distance in the granular flow lubrication system

颗粒润滑介质的宏观剪切流动行为是复杂的，根据颗粒物质剪切流动主要影响机制的不同，可以把剪切颗粒流分为“稀疏剪切颗粒流”和“密集剪切颗粒流”两种类型。“稀疏剪切颗粒流”中的颗粒宏观流动行为主要受颗粒之间二元碰撞作用的影响[35-36]，该方面的研究已经较为成熟。本研究中的颗粒流润滑系统属于“密集剪切颗粒流”类型，影响颗粒润滑介质宏观流动的主要力学因素来源于颗粒间接触力网络[2]。颗粒润滑介质的随机运动行为可以用波动速度T 来进行量化分析[35]，它是决定颗粒润滑介质宏观流动的关键参数，其具体定义如下所示。

在接下来的研究过程中，分析了颗粒润滑介质间摩擦对颗粒流润滑系统宏观流动的影响规律。一般来讲，主要有两个参数来对该变化趋势进行量化分析，一个是颗粒润滑介质的平均速度，另一个就是上述所提波动速度T。分析中，上、下摩擦副间的间隙沿纵向被分为了10 个区域，在每个区域中包含120 个颗粒。平均速度和波动速度T 的统计计算公式如下所示：

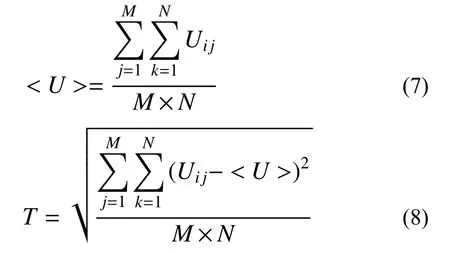
式中，Uij表示第i (i=1, 2, ···, M)个颗粒在j (j=1, 2, ···, N)时步时的速度。

图8 和图9 分别为颗粒润滑介质的平均速度和波动速度沿润滑间隙y 向的的变化规律。分析过程中，颗粒润滑介质间的摩擦系数μ的取值为0.2、0.3 和0.4。如图8(a)所示，颗粒润滑介质的平均速度沿润滑间隙y 向自下而上逐渐减小。越靠近下摩擦副的区域，颗粒润滑介质的流动速度越快，与之相反，越靠近上摩擦副的区域，颗粒润滑介质的流动速度则越慢，这说明颗粒润滑介质的宏观流动行为具有明显的分层特性，如图8(b)所示。图8(b)为颗粒间摩擦系数为0.2、运行时步为5 000 000 时，颗粒流润滑系统的宏观流动图形，图中的颗粒是由右边界流动到左边的，左边出现的颗粒数的多少决定颗粒润滑介质流动速度的快慢(越多，则流动速度越快，反之则越慢)，图中箭头方向清晰的标示出了颗粒润滑介质宏观流动行为的分层特性。在相同的y 向润滑间隙区域，颗粒润滑介质的平均速度随着颗粒间摩擦的增大而减小，这说明颗粒间摩擦对颗粒流润滑系统的宏观流动行为具有抑制作用。

如图9 所示，当颗粒间摩擦系数为0.2 时，颗粒润滑介质的波动速度数值较大，并且波动速度沿间隙y 向自下而上逐渐减小；当颗粒间摩擦系数增大为0.3 时，颗粒润滑介质的波动速度数值亦较大，但波动速度沿间隙y 向自下而上基本上呈逐渐增大的变化趋势；但是，当颗粒间摩擦系数进一步增大为0.4 时，波动速度沿间隙y 向自下而上的变化趋势为先增大后减小，颗粒润滑介质的波动速度数值在靠近上摩擦副的区域非常的小，而且在此情况下波动速度的平均值也明显的小于上述2 种情况。

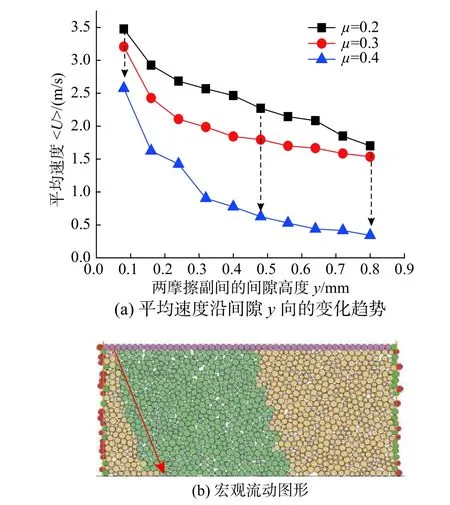
图 8 颗粒润滑介质流动速度的变化规律Fig.8 Variation of the flow velocity of granular lubrication medium

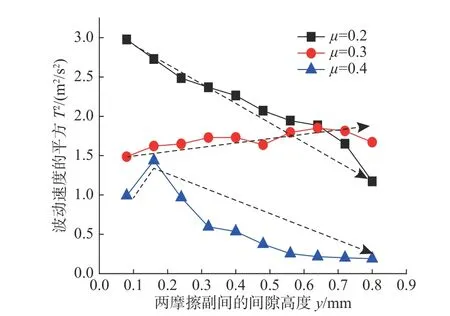
图 9 颗粒润滑介质波动速度的变化规律Fig.9 Variation of fluctuation velocity of granular lubrication medium

从以上的分析结果可以得出，颗粒润滑介质的速度波动直接反映其宏观流动速度的快慢，当颗粒流润滑系统速度波动范围较大时，则会促进颗粒润滑介质的流动，反之，颗粒润滑介质的宏观流动则会减缓，甚至会出现阻塞现象从而导致颗粒润滑介质流动的停止。

3 结论

颗粒润滑介质之间的摩擦会改变颗粒流润滑系统的摩擦学特性，并对系统的力学机制产生影响。为了对此进行研究，构建了颗粒流润滑的离散元数值分析模型，对颗粒润滑介质间摩擦对颗粒流润滑的宏、微观特性和摩擦学影响的力学行为特性进行了分析，研究结果表明：

(1)颗粒间摩擦对颗粒流润滑系统的减摩润滑特性具有显著影响，下摩擦副和颗粒润滑介质之间的平均摩擦系数会随着颗粒间摩擦的增大而增大。

(2)当颗粒润滑介质之间的摩擦系数减小时，颗粒流润滑系统内的微观配位数则随之增大，同时颗粒润滑介质间的微观滑动率亦有相同的变化趋势。

(3)颗粒润滑介质的宏观流动行为具有明显的分层特性，越靠近下摩擦副的区域，颗粒润滑介质的流动速度越快，反之，则越慢；颗粒润滑介质的宏观流动速度随着颗粒间摩擦的增大而减小；颗粒润滑介质的速度波动直接反映其宏观流动速度的快慢，当颗粒流润滑系统速度波动范围较大时，则会促进颗粒润滑介质的流动，反之，颗粒润滑介质的宏观流动则会减缓。

(4)研究颗粒间摩擦对颗粒流润滑影响的力学机制是确定颗粒润滑轴承性能的重要一步，对工程实际中颗粒流润滑轴承的具体理论指导意义为：通过研究颗粒间摩擦的影响，确定合适的颗粒间摩擦性能参数，获得较为顺畅的宏观流动性能，从而为有效提高颗粒流润滑轴承的减摩耐磨性能提供技术支持。