周期驱动双击转子系统中的拓扑相变

景璇，李志坚

（山西大学 理论物理研究所，山西 太原 030006）

0 引言

近年来，各种物理系统如微波远场辐射[1]、原子晶格气体[2]、光子晶体[3-5]等的拓扑特性受到广泛关注。除了静态系统，人们也开始研究周期驱动系统的拓扑特性，发现周期驱动系统具有更丰富的拓扑相[6-8]。时间相关的驱动[9-11]已经作为一种操控量子态的手段被人们大量使用。在一定的周期含时驱动场下，Floquet算符的本征态是局域化[12]的，系统可以出现受拓扑保护的边缘态，从而产生独特的传输特性[13-14]。

在无相互作用的系统中，周期驱动的外场可以使能带结构出现拓扑非平庸相[15]，并且还会出现由非零整数作为拓扑不变量来表征的高阶拓扑相[16-17]，极大地丰富了拓扑相图以及对拓扑相的分类[18-20]。把87Rb玻色-爱因斯坦凝聚体装载于脉冲光晶格中，以凝聚体的质心动量为行走自由度，以其两个超精细基态作为硬币自由度，通过调谐驻波激光强度将单受击转子模型的连续时间周期演化等效为动量空间中的分离时间量子行走，实验上巧妙地实现了在动量空间的可控量子行走[21]，发现在量子共振条件下具有更丰富的拓扑相，而且可拓展到非厄米系统中进行研究[22-23]。文献[17]进一步研究了双击转子模型，它可以等效为劈裂步量子行走，行走自由度的改变依赖于系统的硬币自由度，但在系统的演化过程中，经过每一单步中的两个硬币算符作用后，系统的硬币态回到了初始硬币态。本文在该模型的基础上，再增加一次具有可调参数的硬币算符操作，使得每一单步演化后的硬币态发生改变，研究可调参数对系统的能带结构和拓扑特性的影响。

1 双击转子模型

在冷原子的研究中，冷原子87Rb玻色-爱因斯坦凝聚体中的两个超精细能级52S1/2(f=1)、52S1/2(f=2)和能级52P3/2分别等价为一个三能级原子的两个基态能级和一个激发态能级。把它装载于具有周期势的光晶格中，同时用两束相同频率的驻波激光脉冲对原子进行作用，在激光脉冲的一个周期T中，原子受到强度分别为K1和K2、相隔时间间隔为τ∈(0，T)的两次作用，称为双击转子模型。当驻波激光的频率从三能级原子的激发态调谐至两基态能级之间时，原子基态两能级相对于该驻波激光的失谐为δ=±Δ(Δ＞0)。也就是，对于超精细基态52S1/2(f=1)为正失谐，对于基态52S1/2(f=2)为负失谐。其哈密顿量为

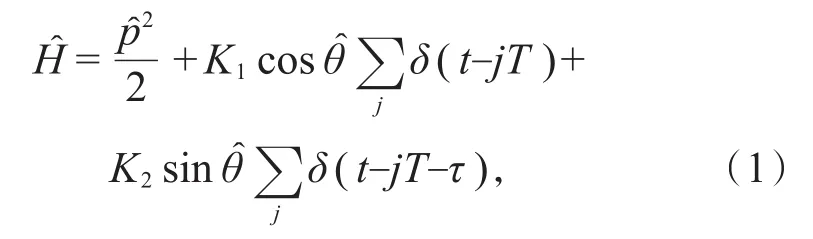
其中和分别是冷原子的位置算符和动量算符，j是脉冲数目，两不同的驻波激光强度，Ω1、Ω2是拉比频率，τp(≪T)是脉冲有效作用时间。这里所有物理量皆是无量纲的，且普朗克常数ℏ设定为1。由于脉冲作用时间τp远小于脉冲周期T，一个完整周期的Floquet算符可以近似表示为

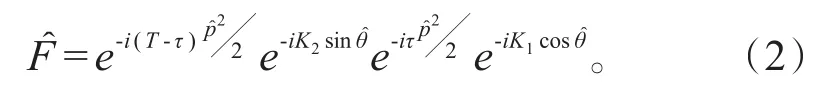
根据脉冲势的空间周期性，原子的动量p可表示为整数部分n∈Z和小数部分η∈(0，1)的和，对于大相干宽度的玻色-爱因斯坦凝聚体，可取η=0。

对于单受击转子模型，在满足量子共振条件T=4π时，Floquet算变为在初态下，其中为动量算符的本征态，φ为两个动量本征态的初始相位差，由决定的动力学演化过程中，当原子受到一次激光脉冲的作用后，平均动量改变为可见，通过选取适当的φ值和K值，使得，实现原子动量从态到态或态的转变。与驻波激光强度成正比，即与原子相对驻波势的失谐成反比。对于相对激光脉冲正失谐的超精细基态52S1/2(f=1)，动量的变化为-1，而对于相对激光脉冲负失谐的基态52S1/2(f=2)，动量的变化为1。这样，可以引入硬币自由度来描述原子的两个内禀基态，从而将由决定的动力学演化过程等价为从初态出发，以原子质心动量为行走自由度，以原子超精细基态作为硬币自由度的一维量子行走[17]。量子行走的条件平移算符由

描述，其中k=Ω2τp/Δ是受击强度。硬币算符通过施加微波脉冲改变两内部态的布居数实现，可表示为

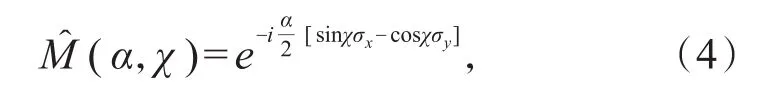
其中旋转角α，χ是实验可调参数，上述中σx，y，z是泡利矩阵。

同理，在量子共振条件T=4π且取两脉冲时间间隔τ=2π下，双击转子系统可以等价为两步条件平移算符作用下的量子行走，即

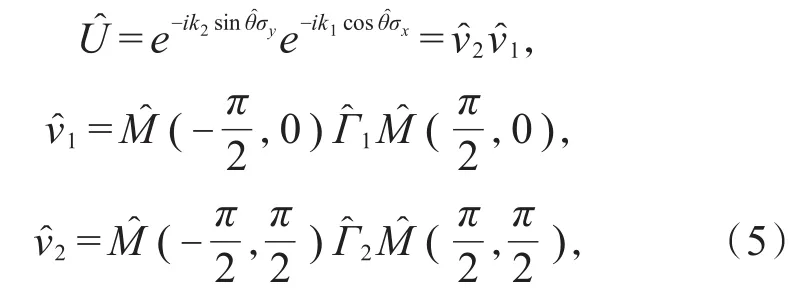
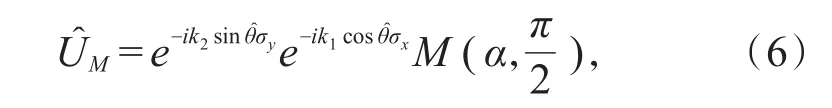
将（4）式代入（6）式中，整理得：

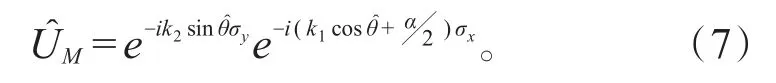
接着，我们讨论该双击转子系统的能级结构和拓扑特性。

2 双击转子模型的能谱及绕数

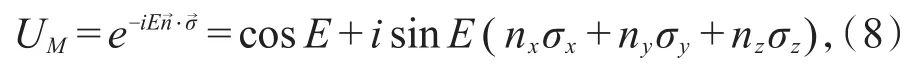
其中n是位置空间布洛赫球上的单位矢量，

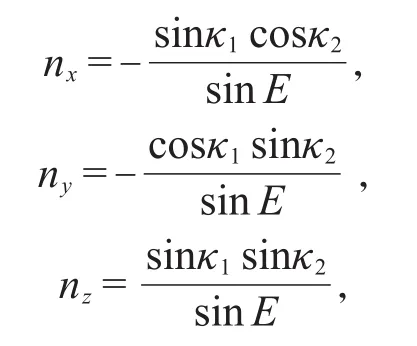
且能量本征值E为

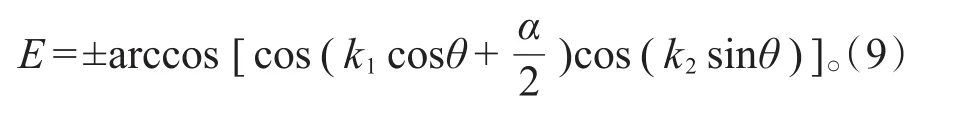
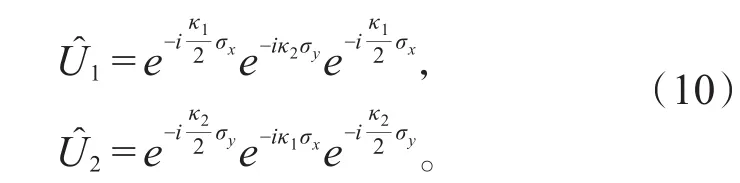
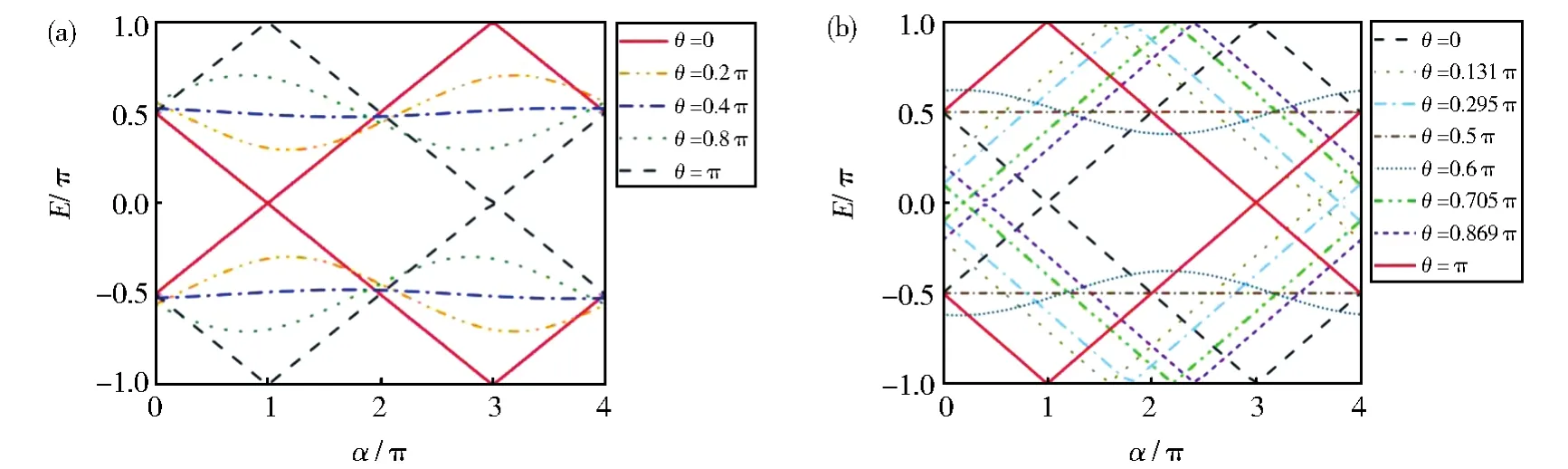
图1 演化算符的本征能E随硬币参数α的变化图，（a）k1=k2=0.5π；（b）k1=3.5π，k2=2.5πFig.1 SpectrumEof Floquet operator versus coin parameterα（a）：k1=k2=0.5π；（b）：k1=3.5π，k2=2.5π

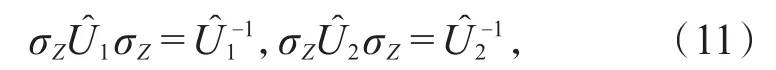
σz是演化算符的手征算符。类似于方程（8），在位置空间中，与对应的单位矢量nl=(nlx，nly，nlz)，l=1，2分别为：

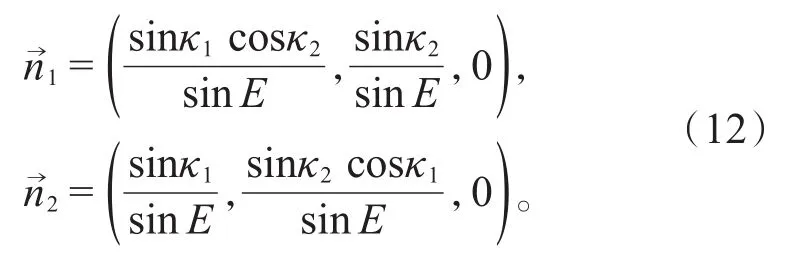
根据绕数的定义

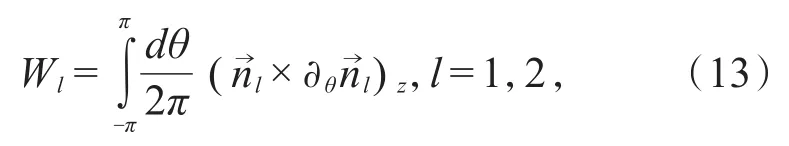
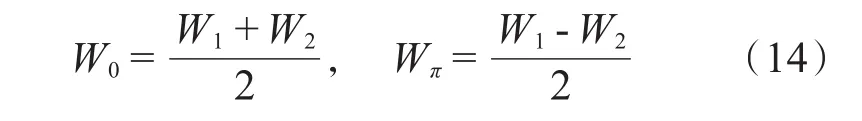
可使得W0的变化只对应0能边缘态，而Wπ的变化只对应π能边缘态。

选取k1和k2的不同取值，图2（a-d）给出绕数W0和Wπ随硬币参数α的变化图。在图2（a）中，k1=k2=0.5π，绕数W0，Wπ同时在参数α=π，3π，5π…处发生突变。与图1（a）的能谱图对比，发现这些α值正好对应着准能量在E=0和E=π处发生带隙闭合。发生拓扑转变的两个不同相由绕数(W0，Wπ)=(1，0)和(0，-1)表征。保持k2固定不变，增大k1值为1.5π，如图2（b）所示，发生拓扑相变的α值保持不变，但绕数 (W0，Wπ)在不同相的取值为 (2，-1)和(1，-2)，出现绝对值大于1的大绕数值。同时增大k1和k2取值，如图2（c）和2（d）中分别选取k1=3.5π，k2=2.5π和k1=k2=3.5π，不仅出现更大的绕数值，而且绕数值随α的变化历经多次突变，系统可存在多个不同的高阶拓扑非平庸相。把图2（c）和图1（b）比较，W0和Wπ发生突变的每个α值分别与两支能谱E在0能和π能闭合时对应的α值一致。

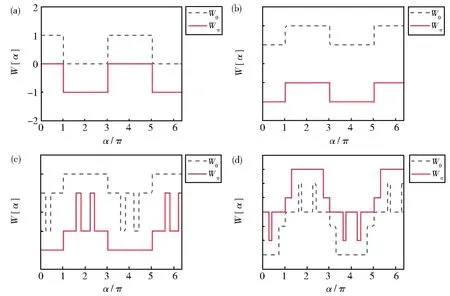
图2 绕数(W0，Wπ)在给定k1，k2值随硬币参数α的变化图，灰（虚）线对应0能闭合处的绕数W0，红（实）线对应π能闭合处绕数Wπ。（a）k1=k2=0.5π；（b）k1=1.5π，k2=0.5π；（c）k1=3.5π，k2=2.5π；（d）k1=3.5π，k2=3.5πFig.2 Winding numbers(W0，Wπ)versusα at fixedk1andk2.Gray（dashed）line means winding numberW0and red（solid）line means winding numberWπ.Panel（a）k1=k2=0.5π；（b）k1=3.5π，k2=2.5π；（c）k1=3.5π，k2=2.5π；（d）k1=3.5π，k2=3.5π

图1中Floquet算符的两支能量线间的带隙闭合与图2中绕数发生突变有着很好的对应关系，正是体-边界对应原理的体现。为了清楚地看到体-边界对应原理，我们把方程（7）作傅里叶变换，在动量空间有：

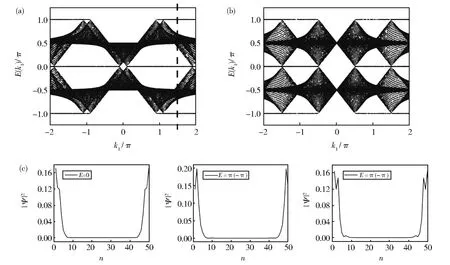
图3 （a）和（b）是当k2=0.5π，α分别为π/5和π时，Floquet能谱E随k1的变化图；（c）是对应（a）图中虚线标记的k1=1.5π时，0和π能本征态在动量格点上的概率分布，横坐标n为动量格点指标Fig.3 （a）and（b）are the Floquet spectrumEversusk1，whenk2=0.5π，α=π/5and π，respectively.（c）showsthe probabilitydistribution of the eigenstates with quasi-energy0and πwhen parameterk1=1.5π in subfigure（a），andnis the index of momentum lattice

3 结论

利用将87Rb玻色-爱因斯坦凝聚体装载于脉冲光晶格中的一维量子受击转子，实验上实现了动量空间的量子行走。在此基础上，本文提出增加使用具有可调参数的硬币算符，旋转每一单步量子行走的硬币态，由该可调参数改变系统拓扑特性的模型。理论上计算了系统的能谱和绕数，结果表明上下能带的带隙在可调参数的变化下，能够在0能和π能处闭合或打开，系统经历拓扑相变，具有拓扑平庸相和拓扑非平庸相。每一个拓扑相由一对绕数来表征，满足体-边界对应原理，在拓扑相的相边界上存在有拓扑保护的边缘态。改变硬币参数，系统可以出现具有大绕数值的拓扑相，丰富了系统的拓扑相图。