CEFR探测器三维空间响应函数敏感性研究

王振忠，喻 宏，胡 赟

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

探测器三维空间响应函数(SRF)通常有两种计算方法[1]：一是通过求解中子输运方程，得到堆芯某处中子源引起的探测器响应，即正向输运计算方法；二是通过求解共轭中子输运方程，得到探测器为共轭源时堆芯各处的中子价值函数，即共轭输运计算方法。其中，共轭输运计算方法可实现一次性全堆芯求解，相比于正向输运计算方法计算时间更少。

目前，探测器SRF多采用离散纵标程序通过共轭输运计算方法计算[2-6]。离散纵标程序中中子注量率分布的计算精度取决于网格划分、能群数目、角度离散数和散射截面展开阶数等因素。通常精细化的计算条件可得到更为精确的SRF结果，对于探测器与堆芯距离较远的钠冷快堆，采用精细化网格划分将会花费巨大的计算资源。因此需研究计算条件对SRF计算的影响。其次，考虑到动态刻棒试验中，堆芯布置和控制棒棒位发生变化，因此需研究堆芯状态对SRF的影响。

本文利用快堆专用多群常数库VITAMIN-FRD[7]和三维离散纵标程序DENOVO[8]，研究中国实验快堆(CEFR)堆芯共轭中子注量率分布形状对计算条件的敏感性。基于共轭输运计算方法，计算三维SRF对控制棒棒位、燃耗累积、装载过程等因素的敏感性。

1 探测器SRF计算方法

1.1 共轭输运计算方法

设探测器中子响应宏观截面为Σd(r0,E)，堆芯内ri处中子源强度S(ri,E,Ω)在堆芯外r0处探测器的响应Rd(ri)可写为：

Σd(r,E)δ(r-r0)dEdΩ

(1)

式中：r为空间位置；E为能量；Ω为角度；Φi为堆芯内ri处中子源在相空间(r,E,Ω)内的中子角注量率；δ(r-r0)为狄拉克函数。当S(ri,E,Ω)为单位强度时，称为探测器关于ri位置的SRF。

假设堆芯ri处中子源为各向同性，根据共轭理论，得到ri处中子源对应探测器空间的响应函数：

δ(r-ri)/4πdEdΩ

(2)

式中：χ(r,E)为裂变谱；Φ*为相空间(r,E,Ω)内的共轭中子角注量率。

式(1)、(2)分别对应正向输运计算方法和共轭输运计算方法计算公式。采用共轭输运计算方法时，往往需要对计算模型全区域进行精确的共轭中子注量率计算。在实际计算中感兴趣区域为燃料组件(有裂变源)区域共轭中子注量率，并非计算模型全区域。

按探测器总响应值归一化探测器SRF，可得到体积元Vi内中子源对探测器响应值的贡献份额w(i)为：

(3)

式中，V为反应堆堆芯所包含的体积。

对于空间和能量离散，则w(i)可表示为：

(4)

式中：ΔVi为体积元Vi的体积；(ΔE)g为g群能量宽度；Φ*(ri,Eg)为ri处能量为Eg的共轭中子注量率分布；G为能群数；N为堆芯节块数。

若对分子和分母中Φ*进行归一化处理，w(i)不受影响，即w(i)与Φ*数值无关，与Φ*分布形状有关。

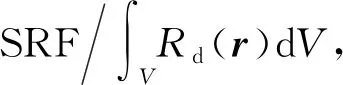
1.2 计算流程

根据式(4)可知，计算探测器SRF需确定反应堆裂变谱和共轭中子注量率分布。采用临界蒙特卡罗程序KENO-Ⅵ[9]计算堆芯裂变源分布(按指定网格统计)；共轭中子注量率由三维SN程序DENOVO求解。具体计算流程如下。

1) 多群数据库制作

利用PASC截面处理程序包[10]将多群主库VITAMIN-FRD制作为AMPX工作格式数据库(KENO-Ⅵ使用)和ANISN宏观截面数据库(DENOVO使用)。

2) 裂变源计算

利用KENO-Ⅵ对反应堆堆芯区域建模和临界计算，按照DENOVO共轭计算时网格统计裂变源分布，并转存为裂变源文件。

3) 共轭中子注量率计算

建立以探测器为共轭源的全区域计算模型，利用DENOVO进行共轭输运方程求解，得到共轭中子注量率分布文件。

4) SRF计算

根据式(4)自编计算脚本程序，读取裂变源文件和共轭中子注量率分布文件，进行探测器SRF计算，并根据图1网格与组件位置转换关系，计算对应组件三维SRF。

2 计算模型

CEFR是我国建成的首座池式钠冷快堆[11]，钠池内探测器位于石墨屏蔽柱区域。故计算模型包含堆芯区域、围板、钢套屏、石墨屏蔽柱和探测器。堆芯区域组件包含中子源组件、燃料组件、控制棒组件(安全、补偿、调节)、钢反射组件、硼屏蔽组件和模拟组件。与燃料棒及冷却剂通道尺寸相比，堆芯区域快中子平均自由程较长[12-13]，计算模型中所有组件均采用组件栅元内均匀化描述。堆芯外区域围板、钢套屏、石墨屏蔽柱采用均匀化描述。探测器位于石墨屏蔽柱区域内，中心点距堆芯中心位置226.5 cm，中心点与堆芯中心位置高度对齐。CEFR首次临界堆芯和探测器布置如图2所示。以图2中箭头起始位置为原点(高度对应堆芯活性区中心)，建立如图2所示的坐标轴，其中z轴方向垂直于纸面向外。

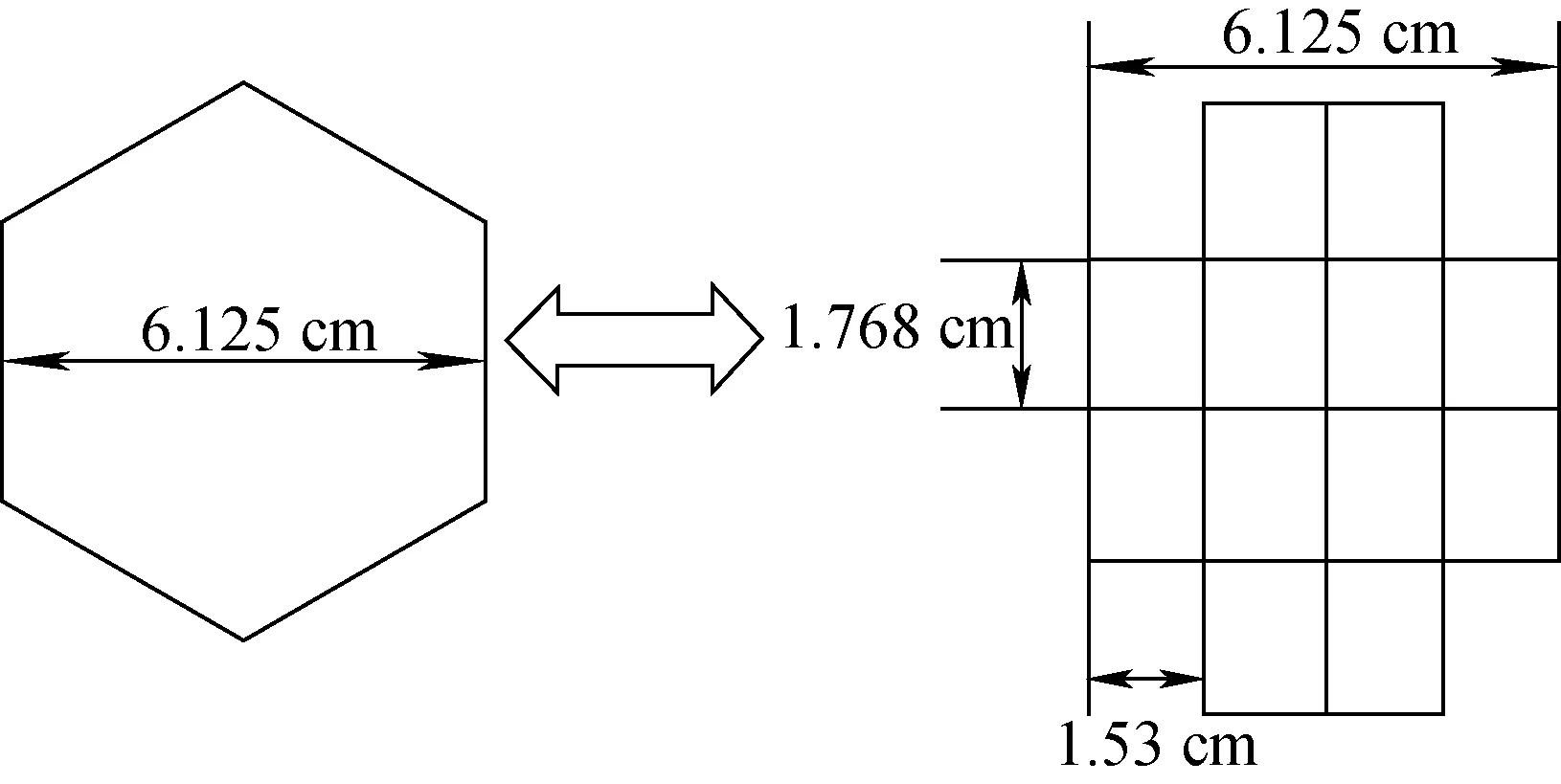
图1 六角形组件直角网格等效划分示意图 Fig.1 Conversion between hexagonal cross section of subassembly and rectangular grid

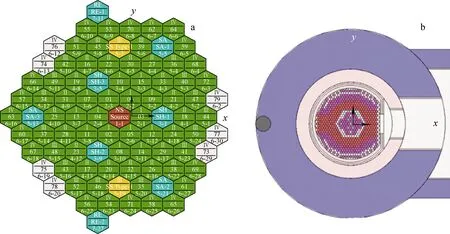
图2 CEFR首次临界堆芯(a)和探测器(b)布置Fig.2 Core (a) and detector (b) layout of clean-core criticality state of CEFR

3 结果与讨论

3.1 共轭中子注量率分布形状对计算条件的敏感性

大尺度中子输运确定论计算，中子输运结果主要受模型网格尺寸、截面数据库的能群结构、角度离散数和散射截面展开阶数等影响。选取过原点沿坐标轴方向的网格内共轭中子注量率分布形状为研究对象，研究网格划分、能群数目、角度离散数和散射截面展开阶数对共轭中子注量率分布形状的影响，获取平衡计算精度和计算资源开销的优化方案。

燃料组件区域采用固定宽度网格(远小于平均自由程(约为10 cm)，如图1所示)划分，以保证燃料组件区域共轭中子注量率分布形状的计算精度。采用探测器总响应值归一化后，得到燃料组件区域共轭中子注量率分布形状，如图3所示。

1) 能群数目的影响

参考CEFR物理、屏蔽设计中采用的截面数据库——NVITAMIN-C[11]的能群结构，将VITAMIN-FRD经过MALOCS模块[10]精简为171群数据库。使用171群与514群截面数据库计算的共轭中子注量率分布形状如图3a所示。由于误差传递，能群数目改变后在远离探测器区域共轭中子注量率分布形状偏差增大。以能群划分较为精细的514群数据库计算结果为参考解。随所处位置与探测器距离的增加，171群共轭中子注量率分布形状与参考解的相对偏差由12%增大到25%。因此，计算中采用514群截面数据库。

2) 角度离散数(SN)和散射截面展开阶数(PN)的影响

快堆堆芯燃料组件区域中子平均自由程长，且中子注量率角分布各向异性比堆芯外区域弱，采用S8、P3与S16、P5近似时共轭中子注量率分布形状的相对偏差小于3%，如图3b所示。因此采用S8、P3近似可在保证计算精度的前提下降低计算资源。

3) 网格划分的影响

随网格宽度的增加，几何描述精度降低，输运方程求解的误差增加。以5 cm宽网格的计算结果为参考解，由图3c可见，粗网格共轭中子注量率分布形状与参考解的相对偏差，随所处位置与探测器距离的增加而增大，随网格宽度的增加而增大。当网格宽度为10 cm时，共轭中子注量率分布形状与参考解的最大相对偏差出现在远离探测器区域(约14.2%)。在远离探测器区域共轭中子注量率分布形状低，对探测器贡献小，可认为对探测器SRF计算影响较小。因此，在粗网格条件下(≤10 cm)可获得有效的共轭中子注量率分布形状。

共轭中子注量率分布形状对能群数目的敏感性较高，但对网格尺寸、角度离散数和散射截面展开阶数的敏感性较低。探测器SRF计算时，可使用低计算条件(网格宽度为10 cm，514群截面数据库，S8、P3近似)的共轭中子注量率分布形状预估高计算条件(网格宽度为5 cm，514群截面数据库，S16、P5近似)时计算结果。

3.2 SRF对堆芯状态的敏感性分析

反应堆运行过程中存在着燃料组件装载、控制棒棒位改变、燃耗累积等堆芯状态变化都会对探测器响应造成一定的影响。通过研究探测器SRF对堆芯状态参数的敏感性，可建立探测器SRF插值表，供动态刻棒试验中使用。

CEFR净堆临界堆芯布置时，堆芯中所有组件对钠池内探测器均有贡献，如图4所示。径向上，组件内SRF随所处组件与探测器距离的增加而减小；轴向上，组件内SRF关于堆芯中心点对称，随所处位置与堆芯中心点距离的增加而减小。

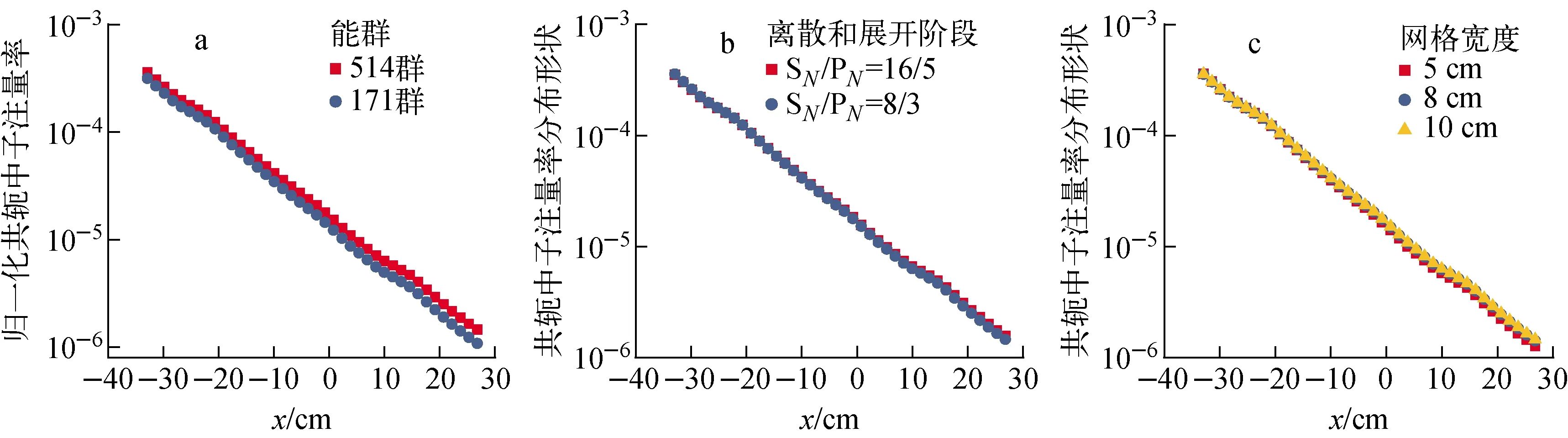
图3 共轭中子注量率分布形状Fig.3 Shape of adjoint neutron fluence rate

1) 控制棒位置的影响

反应堆运行时控制棒处于临界棒位附近。本文以控制棒两种极限状态(全部插入堆芯(ARI)和全部拔出堆芯(ARO)状态)为例，研究控制棒棒位对组件内SRF的影响。

控制棒插入堆芯前后，堆芯中心区域和靠近探测器区域的组件内SRF变化明显，如图5所示。其中，图5a是利用SN程序基于共轭输运计算方法的计算结果，图5b是利用CADIS方法的蒙特卡罗(简称蒙卡)偏倚输运[14-16]，基于正向输运计算方法的计算结果。由图5可看出SN与蒙卡求解结果符合良好。控制棒插入堆芯前后，控制棒对组件内SRF影响与控制棒在堆芯所处位置有关：随控制棒位置与探测器距离的增加，控制棒对其周围组件内SRF的影响越小。控制棒插入堆芯后，吸收体吸收位于控制棒的远离探测器侧的组件内中子，使对应组件内中子难以到达探测器，造成对应组件中子对探测器响应的贡献降低。控制棒距探测器越近，位于控制棒的远离探测器侧的组件数越多，该控制棒对组件内SRF的影响也就越大。

a——径向；b——轴向图4 净堆临界堆芯布置组件内SRF的分布Fig.4 SRF distribution of clean-core layout

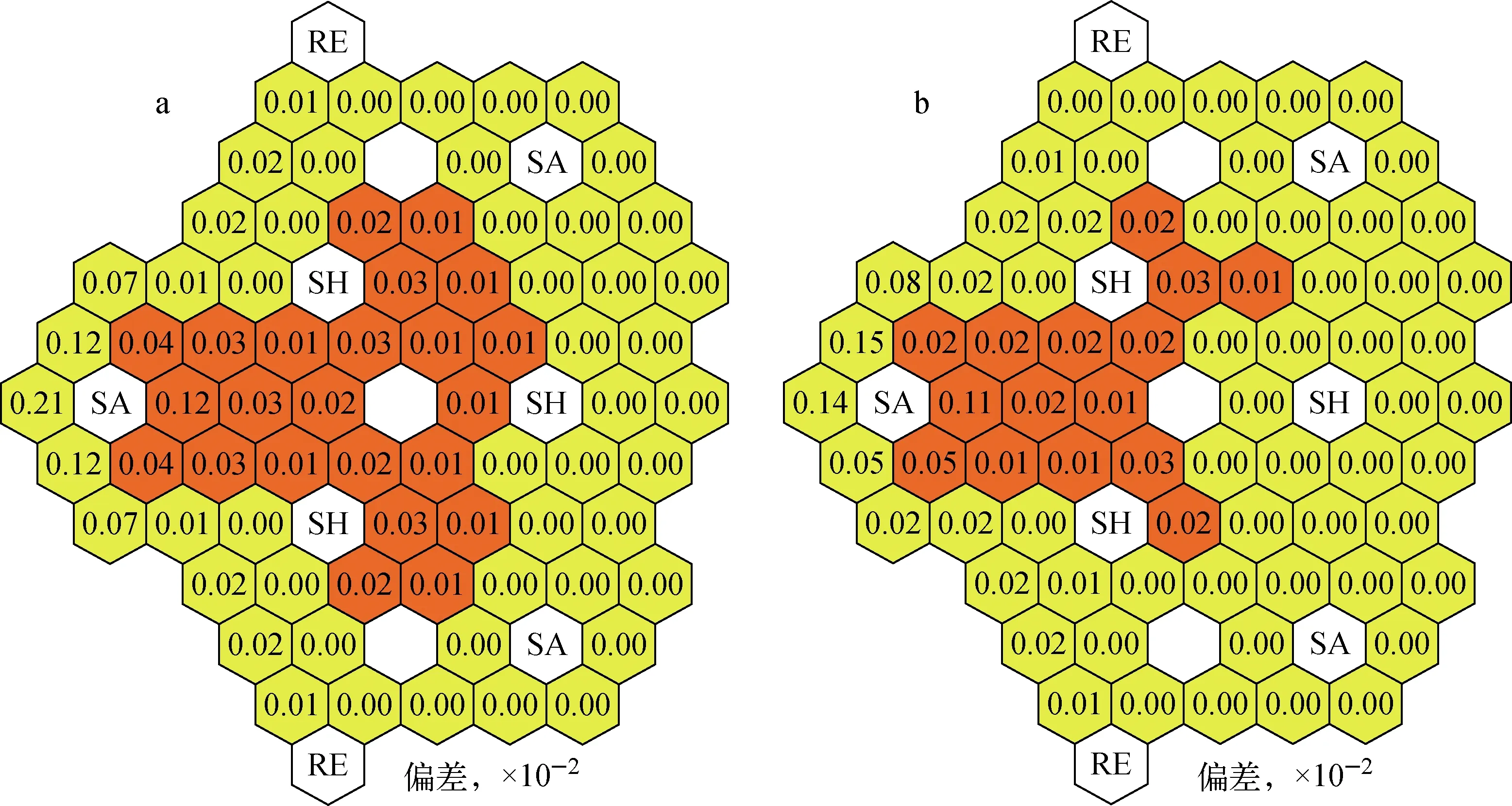
红色为负值，黄色为正值；为便于显示，截断值为1×10-4；偏差=SRFARI-SRFARO a——SN方法；b——蒙特卡罗方法图5 组件内SRF径向偏差分布Fig.5 Radial deviation distribution of SRF

另一方面，控制棒对周围组件内SRF的影响也与控制棒和组件之间的相对位置有关：组件位于控制棒的靠近探测器侧时，控制棒插入后会使组件内SRF增加；组件位于控制棒的远离探测器侧时，控制棒插入后会使组件内SRF减小。

控制棒插入堆芯前后，选取最靠近探测器的控制棒组件(5-13，如图2a所示)的相邻6盒燃料组件，其组件内SRF的相对偏差轴向分布如图6所示。控制棒位于ARI与ARO状态时，相对偏差最大的组件是位于控制棒的远离探测器侧的组件(4-10)；相对偏差随组件位置由控制棒的远离探测器侧向靠近探测器侧的移动而减小。这说明控制棒对周围组件内SRF轴向分布的影响也与控制棒和组件之间的相对位置有关。

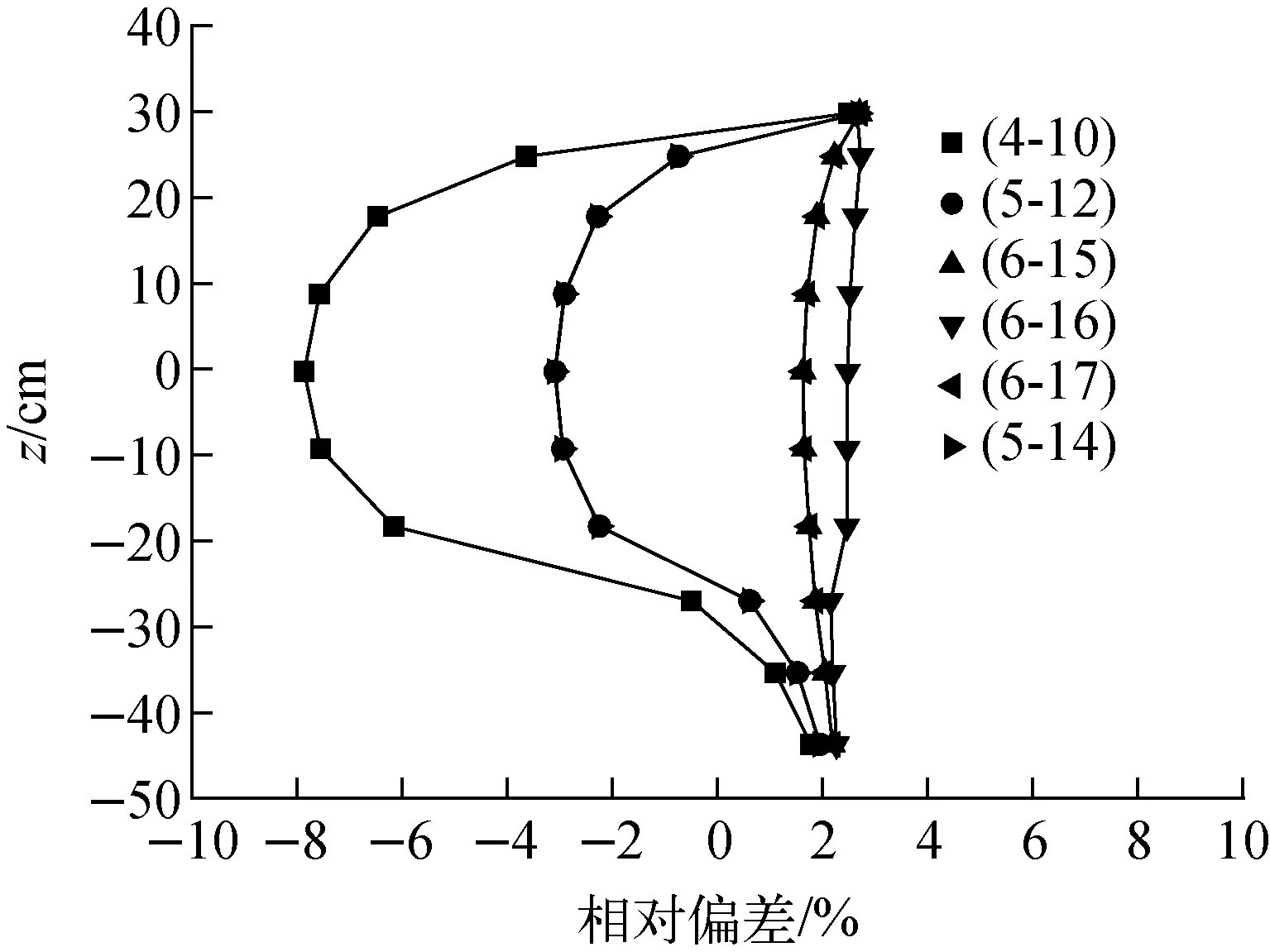
相对偏差=(SRFARI-SRFARO)/SRFARO×100%图6 组件内SRF的轴向相对偏差分布Fig.6 Axial relative deviation distribution of SRF

2) 装载过程、燃耗累积的影响

CEFR首次临界和首炉堆芯布置之间，堆芯燃料组件数目相差7盒(如图2a中灰色组件所示)。装载组件前后，组件内SRF的偏差随所处组件与探测器距离的增加而减小；新装载组件对装载位置周围组件的SRF未产生明显影响，即燃料组件内SRF对新装载组件在堆芯所处位置不敏感，如图7a所示。

平衡态堆芯布置寿期初与寿期末相比，燃料组件内SRF偏差均小于0.001，如图7b所示，表明燃耗累积对组件内SRF的影响不明显。

相对于控制棒插入和燃耗累积，燃料组件装载对组件内SRF的影响更大。控制棒对组件内SRF的影响与控制棒在堆芯中所处位置有关；组件内SRF受控制棒影响程度与该组件和控制棒相对位置有关。燃耗累积对组件内SRF影响并不明显。

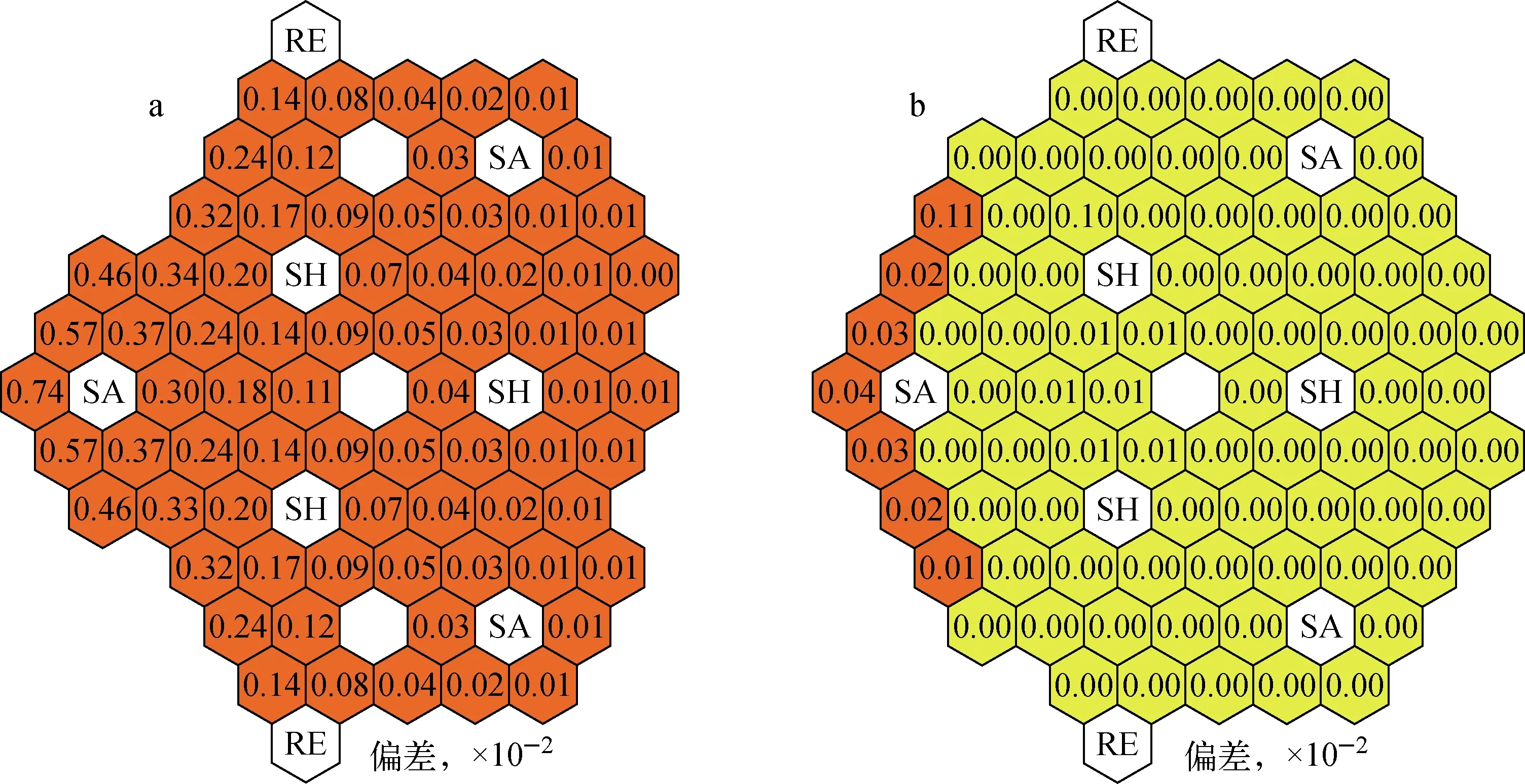
图7 组件内SRF径向偏差分布Fig.7 Radial deviation distribution of SRF

4 结论

本文使用SN程序对CEFR钠池内探测器SRF进行了计算，主要对具有大尺寸、深穿透问题的探测器SRF计算模型中共轭中子注量率对计算条件的敏感性、钠池内探测器SRF对堆芯状态的敏感性进行了分析，可得出以下结论。

1) 堆芯燃料组件区域共轭中子注量率分布形状对网格宽度、角度离散数和散射截面展开阶数的敏感性较低，可利用低计算条件的共轭中子注量率分布形状预估高计算条件下计算结果。

2) CEFR钠池内探测器SRF随组件与探测器距离的增加而减小。与压水堆不同，CEFR堆芯内组件对探测器贡献均较为明显。

3) 燃料组件装载对组件内SRF的影响不可忽略；控制棒对组件内SRF的影响与探测器在堆芯所处位置、组件和控制棒相对位置有关，但总体上控制棒对堆芯组件内SRF的影响不大。

从动态刻棒方法看，基于共轭输运计算方法，使用SN程序可快速、有效地计算出CEFR钠池内探测器SRF，便于CEFR控制棒刻度(换料后)时探测器SRF的重新计算。

本文可对CEFR堆容器外探测器和示范快堆(大型钠冷快堆)探测器SRF计算提供方法和技术参考，为快堆领域选择合适探测器安装位置提供理论依据，为快堆实现动态刻棒提供技术积累。