HFE-7100工质稳态临界沸腾传热实验研究

范晓光，杨 磊，邬立岩,*

(1.沈阳农业大学 工程学院，辽宁 沈阳 110866；2.辽宁石油化工大学 石油化工学院，辽宁 抚顺 113001)

池沸腾是高效的相变传热方式之一，已广泛应用于核能工程、石油化工及电子工业等重要领域。沸腾临界点是核化沸腾与膜状沸腾之间的转换点，对应的热通量为沸腾临界热通量(CHF)，也通常被称为“沸腾危机”，其决定了换热器件的安全稳定运行状况及工况的适用范围，是核反应堆等装置设计中的重要热工限值，获得一定工况下的临界热通量对于反应堆的安全运行具有举足轻重的意义。池沸腾临界热通量的触发机理较为复杂，其值主要由气泡聚集程度及液相补充能力所决定，而二者受到沸腾工质物性[1]、表面尺度构型[2-3]、表面润湿性[4-5]及实验操作工况等因素的显著影响。

尽管目前尚未将HFE-7100作为核能领域的主要传热工质，但其高稳定性、强润湿性、无毒害性及低全球变暖潜能值的优点使其具备在该领域的应用潜力。因此仍需补充能作为导热介质的HFE-7100工质的池沸腾传热基础数据，深入分析表面粗糙度及饱和压力对池沸腾临界热通量的作用机理。本文考察不同饱和压力条件下HFE-7100工质在光滑及粗糙表面的稳态临界沸腾传热，对沸腾临界状态下的工质沸腾相变动态过程进行可视化研究，并测试不同工况下的沸腾临界热通量。采用的铜基表面平均粗糙度范围为0.019～0.587 μm，饱和压力试验范围为绝压0.07～0.20 MPa。同时本文将临界热通量实验数据与相关预测模型进行对比，并通过引入代表表面粗糙度及饱和压力的相关无因次参数建立临界热通量参数K预测关联式。

1 实验系统及过程

1.1 实验系统

工艺流程如图1所示，主要包括沸腾传热系统、冷凝及冷却循环系统和数据采集系统。沸腾传热系统包含柱状导热铜块、沸腾传热器件、圆柱状加热器(0.25 kW/支，共6支)及辅助加热器(1.25 kW)；冷凝及冷却循环系统包括板式冷凝器、冷却水循环系统及R-134a工质冷却循环系统；数据采集系统包括NI9220数据采集器、LabVIEW数据采集程序、压力传感器及热电偶。本研究通过机加工及砂纸打磨制备了4种具有不同表面粗糙度的沸腾传热器件，沸腾传热器件(圆柱形，直径40 mm、高5 mm)与导热铜块通过焊锡焊接；根据调节冷却水循环温度、流量及辅助加热器功率来调控4个实验系统饱和压力工况。系统饱和压力由压力传感器测试得到，同时通过布置沸腾腔室内的3只热电偶(其中2只用于测试液相工质，1只用于测试气相工质)来监测工质温度，并通过测试得到的饱和温度及饱和压力共同检测系统稳定状态。测量沿垂直方向布置于导热铜块中心的6支热电偶温度(垂直间距为5 mm)，来计算导热铜块内的温度梯度，并根据傅里叶导热定律计算沸腾传热通量。每组实验均从核化沸腾起始点加热至临界状态，实时监测特定实验工况条件下沸腾传热通量的变化趋势，测试得到的最高热通量即为沸腾临界热通量。为排除系统内不凝气对实验数据的影响，采用真空泵对沸腾腔室进行抽吸。沸腾实验数据均在测试温度及系统压力稳定5 min后进行数据采集。在每种实验工况条件下，重复测试3组临界热通量实验数据。

1.2 表面加工及表征

通过加工4种具有不同粗糙度的铜基表面来考察表面粗糙度对临界状态下沸腾传热的影响。光滑铜基表面由机加工(Nanotech 250UPL)制作，粗糙表面分别由1200#、600#及320#砂纸打磨制备。采用扫描电子显微镜(LEO 1455VP)考察沸腾传热表面形貌，如图2所示。由图2可知，机加工的光滑表面较平整，粗糙表面的凹槽深度及宽度随着砂纸粒度的减小而明显增大。

为定量分析铜基表面粗糙程度，采用3D表面轮廓仪(ZYGO)测试表面平均粗糙度Ra、均方根粗糙度Rq及峰间平均宽度Rsm等特征参数。4种表面的平均粗糙度范围为0.019～0.587 μm，具体数值列于表1。

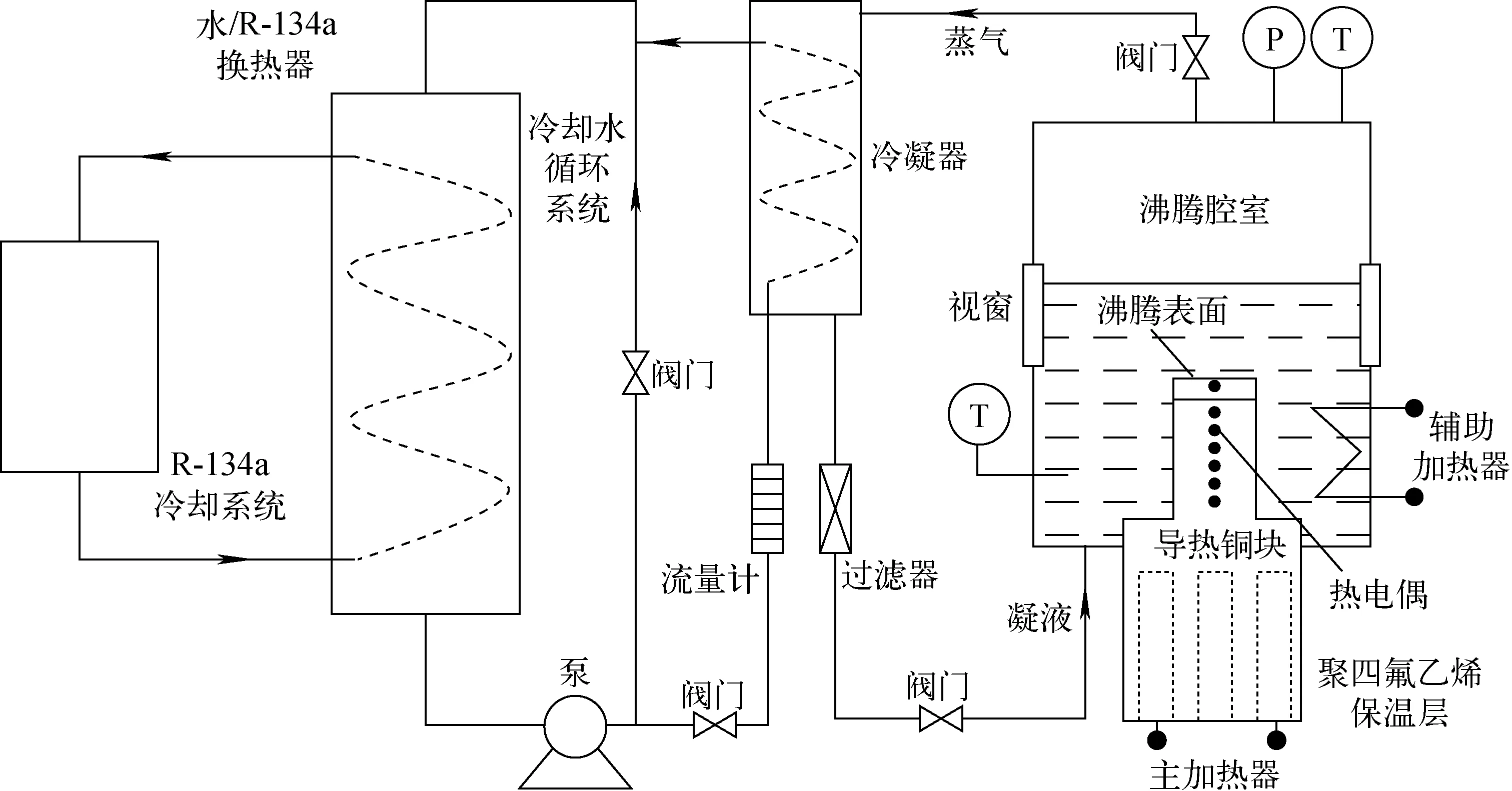
图1 池沸腾实验系统流程图Fig.1 Flow chart of pool boiling facility

图2 铜基沸腾传热表面扫描电镜图像Fig.2 SEM image of copper boiling surface

表1 铜基表面粗糙度参数Table 1 Roughness parameters of copper surfaces

图3示出了20 ℃条件下HFE-7100工质在4种不同粗糙表面的接触角θ。由图3可知，HFE-7100工质在铜基表面的接触角随表面粗糙度的增加而略有下降，其在室温下的接触角介于7°～10°之间，为高润湿性工质。

图3 20 ℃条件下HFE-7100工质 在不同粗糙度铜基表面的接触角Fig.3 Contact angle of HFE-7100 on copper surfaces with different roughnesses at 20 ℃

1.3 数据处理

通过测量沿垂直方向布置于导热铜块中心的6支热电偶温度(垂直间距为5 mm)来计算导热铜块内部的温度梯度，进而根据傅里叶导热定律计算沸腾传热通量：

(1)

式中：Xi为测试热电偶所在位置与导热铜块表面之间的距离差；Ti为位置Xi所对应的测量温度；kCu为铜基的导热系数。

实验采用的热电偶由标准铂电阻(PT5218)进行校正，校正后的不确定度为±0.1 K；压力传感器由高精度标准压力表(YB200，精度0.4级)校验，校验后的不确定度为±2 kPa。影响沸腾临界热通量实验误差的测量值为热电偶温度(不确定度为±0.1 K)及热电偶分布位置(不确定度为±0.02 mm)，根据Moffat[25]提出的误差分析方法计算得到的沸腾临界热通量测试误差范围为1.5%～2.7%。

2 实验系统及机理分析

2.1 稳态临界沸腾可视化研究

池沸腾相变传热通常表现为核化沸腾、临界沸腾、过渡阶段(核化沸腾向膜状沸腾转换)及膜状沸腾，在特定工况下稳态临界沸腾状态具有最高的传热能力，即临界热通量高于其他阶段沸腾传热量。本文对临界沸腾及沸腾过渡阶段进行了可视化实验研究。图4为HFE-7100工质在表面粗糙度为0.587 μm铜基表面且饱和压力为0.10 MPa条件下的稳态临界状态及过渡阶段的沸腾可视化图像，对应的传热通量分别为205.1 kW/m2及194.7 kW/m2。

沸腾临界状态下的气相工质表现为小气泡、大气泡、气柱及蘑菇状气团等形态。沸腾表面始终由不同尺度气泡所覆盖，小气泡主要通过核化生长形成，大气泡主要由小气泡合并形成并向上运动脱离沸腾表面，如图4a、b所示。不规则形状的大气泡在上升过程中会进一步融合成气柱，形成蒸气脱离沸腾表面通道，如图4c所示。同时气柱沿径向发生脉动并向上部液相工质主体喷射蘑菇状气团以实现气相工质的有效分离，如图4d、e所示。随着沸腾表面温度进一步升高，沸腾过程会由临界状态向过渡阶段发生转换。沸腾表面基本由不平整的气膜所覆盖，气泡以分散状态不断从气膜分离，但向上运动的气泡并未合并成大气团或气柱，如图4f～j所示。通过对比两组沸腾实验图像可知，稳态临界沸腾状态下，大量蒸气从沸腾表面脱离，气液两相运动非常剧烈，形态更为多样化，而沸腾过渡阶段的气相分离过程较为单一。

图4 稳态临界状态(a～e)及过渡阶段(f～j)的沸腾可视化图像Fig.4 Pool boiling visual images for critical state (a-e) and transitional state (f-j)

2.2 沸腾临界热通量研究

图5 表面粗糙度及饱和压力对临界热通量的影响Fig.5 Effects of surface roughness and saturated pressure on critical heat flux

为准确获得4种饱和压力条件下具有不同表面粗糙度铜基表面的池沸腾临界热通量数据，针对每种实验工况，分别重复测试3组临界热通量实验数据，如图5所示，测试得到各工况下临界热通量的标准偏差范围为3.57～5.13 kW/m2，对应的离散系数的范围为1.39%～3.36%。同时实验数据表明，表面粗糙度及饱和压力均对沸腾临界热通量产生积极作用。图6示出了以光滑表面(Ra=0.019 μm)在0.07 MPa条件下的临界热通量为基准值，不同实验条件下的临界热通量提升率，提升率范围为14.9%～76.0%。同时以4种沸腾传热表面0.07 MPa饱和压力条件下的临界热通量为基准，0.10、0.15及0.20 MPa饱和压力条件下的临界热通量分别平均提升8.9%、29.7%和44.2%；而以光滑表面在4种饱和操作压力条件下的临界热通量为衡量标尺，表面粗糙度为0.205、0.311、0.587 μm的沸腾传热表面对应的临界热通量分别平均提升6.8%、10.9%和17.9%。相较而言，在本实验测试工况条件下，饱和压力对沸腾临界热通量影响更为显著。

图6 临界热通量提升率Fig.6 Enhancement ratio of critical heat flux

影响沸腾临界热通量的关键因素是相变过程中气泡的力学参数及液相的补给能力。结合可视化实验图像及相关物理模型(沸腾气液两相二维结构)[16,26]，本文描绘了微尺度空间内临界状态下的沸腾传热过程，如图7所示。合并形成的大蒸气团覆盖于核化气泡、蒸气喷射柱、液相边界层及沸腾传热表面之上，气相连续向上运动，而液相工质不断补给以维持稳态的沸腾相变传热，二者达到平衡状态且达到传热通量上限，即处于沸腾临界状态；而随着热量传递能力的降低及表面温度的迅速增加，小气泡及蒸气喷射柱不断沿水平方向扩增直至覆盖于沸腾表面，液相无法有效补给，即达到核化沸腾向膜状沸腾转换的过渡阶段。因此液相在沸腾表面的铺展润湿、气相沿水平方向的扩增及液相边界层厚度决定了沸腾表面的临界传热能力。

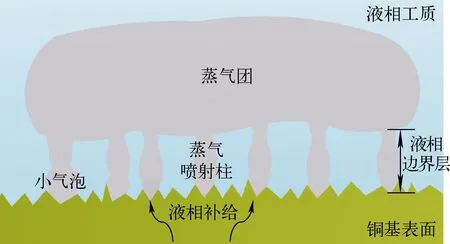
图7 沸腾临界稳态传热过程示意图Fig.7 Schematic diagram of pool boiling process at critical state

系统饱和压力的变化对工质热物性作用显著，因此会对气相沿水平方向扩增移动及液相边界层厚度产生影响。同时，沸腾传热表面粗糙度会对液相工质在表面的铺展润湿性能产生效应，从而决定了液相有效补给的程度。Kandlikar[21]指出沸腾气泡会受到由相变蒸发引起的动量扩增力而不断沿水平方向移动扩增，当气泡增至一定程度，气相会发生合并聚集形成气膜，引起核化沸腾向膜状沸腾的转换，同时针对水平动量扩增力FM建立了模型关联式，表达式如下：

(2)

(3)

(4)

式中：Hb为气泡高度；Db为气泡直径；qI为气泡相界面传热通量；hLV为气化焓；σ为表面张力；ρ为密度。

图8示出了根据水平动量扩增模型，针对光滑及平均粗糙度为0.587 μm的铜基表面在4种不同饱和压力及相界面传热通量条件下，计算得到的气泡扩增力。结果表明，系统饱和压力及相界面传热通量对气相水平扩增动量影响显著，而表面粗糙度的作用并不明显，系统饱和压力越低，传热通量越大，水平动量扩增力越大，气泡更易沿水平方向增长。

图8 不同表面粗糙度及饱和压力条件下的 气泡水平动量扩增力Fig.8 Force due to change in momentum under different surface roughnesses and saturated pressures

Haramura和Katto[18]认为气泡的生长是通过消耗液相边界层内的液体工质来实现，而沸腾临界状态是由大气泡脱离之前液相边界层内液体全部蒸发所触发，并根据Helmholtz不稳定性建立了液相边界层预测模型。随后Rajvanshi等[27]运用电子探针对水及醇类工质的液相边界层厚度进行了测试，并建立了预测关联式，实测值与预测值吻合较好，其预测值为Haramura和Katto建立的模型[18]计算值的2倍，如式(5)所示。由于相变沸腾过程中气泡生长及分离会发生周期性变化，对液相边界层有一定扰动作用，进而对边界层恢复周期产生影响，Zhao[28]及Ding[29]对液相边界层的恢复周期建立了预测模型，表达式如式(6)所示。

(5)

(6)

式中：δ为液相边界层厚度；t为液相边界层恢复时间；kL为液相热导率；αL为液相热扩散系数；ΔT为过热度。

图9示出了系统饱和压力对液相边界层厚度及恢复周期的影响。结果表明，系统饱和压力越高，具有的液相边界层厚度越大，液相边界层受气泡扰动恢复周期越短，而液相边界层增厚及快速恢复更利于为相变沸腾提供液相工质补给及缓冲液相边界层内工质的温度变化，不易在表面形成干斑，从而阻碍气泡或喷射柱在沸腾表面聚集。

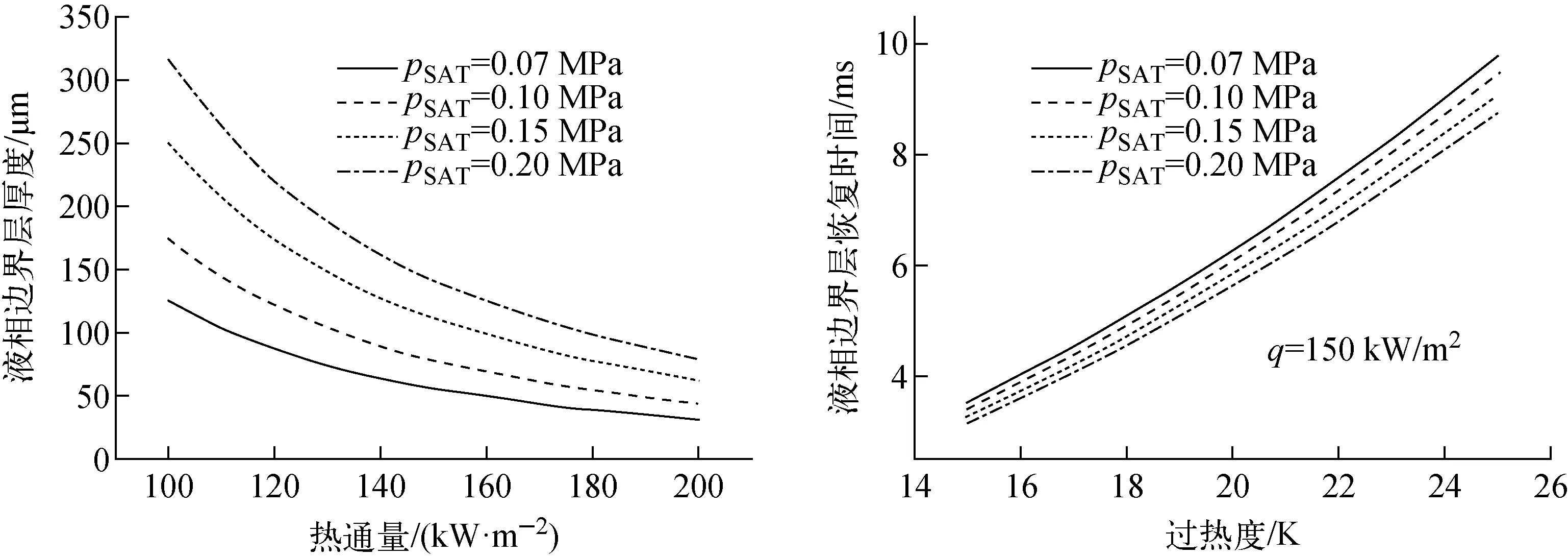
图9 饱和压力对液相边界层厚度和恢复时间的影响Fig.9 Effect of saturated pressure on thickness and recovery time of liquid layer

粗糙度反映了表面微观几何形状特性，Quan等[22]及Kim等[30]指出微纳尺度结构表面会影响表面液相工质的毛细作用力，使液相在表面的铺展润湿过程发生改变，进而引起沸腾表面在临界状态传热能力的改变，在微重力反应条件下也具有同样效果[31]。Kim等[30]对相变过程中表面粗糙度对液相工质的毛细流动速度的影响作用建立了预测模型，表达式如下：

(7)

式中，μ为工质黏度。

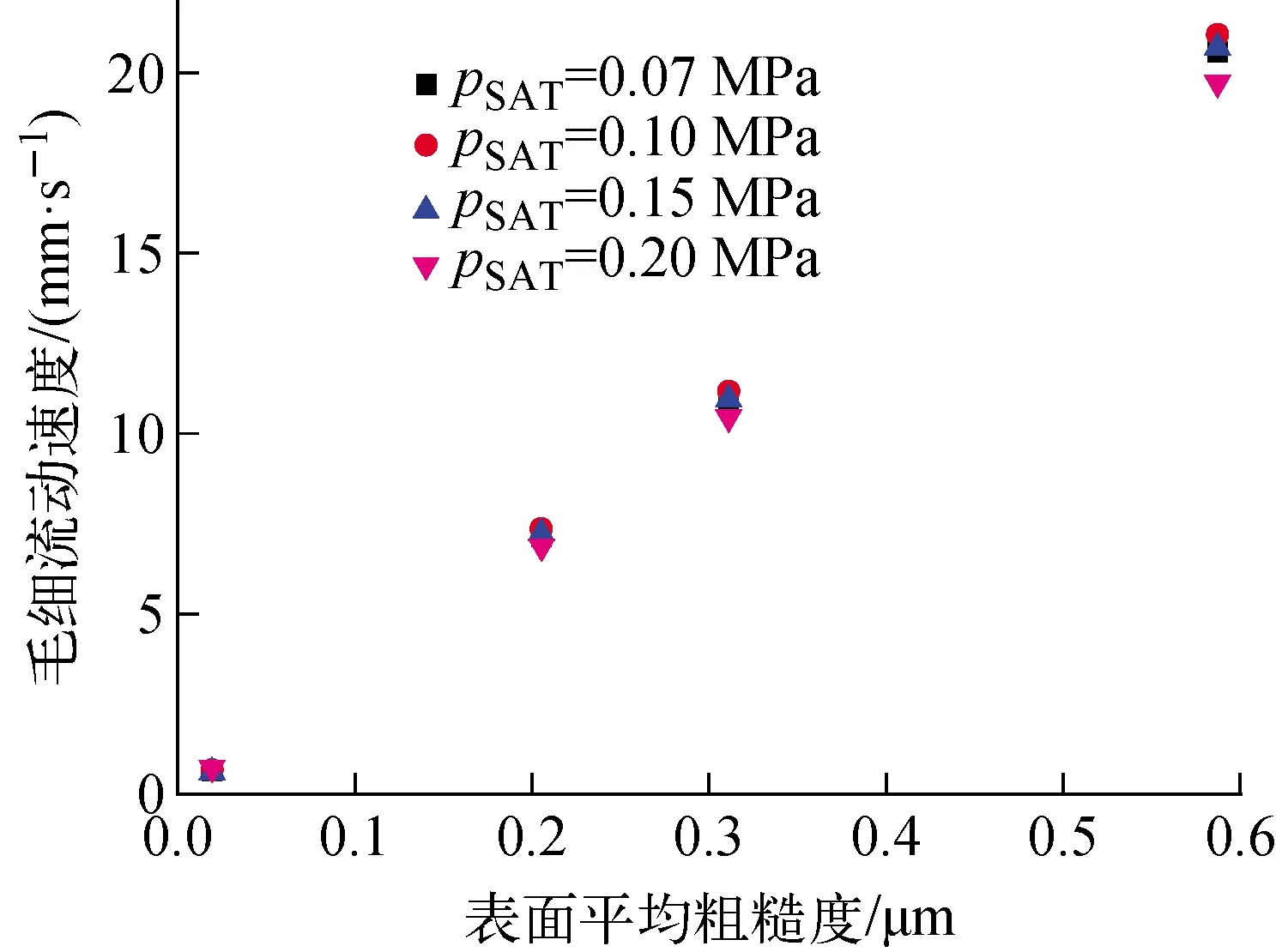
图10 不同饱和压力及表面粗糙度条件下的 液相毛细流动速度Fig.10 Capillary flow velocity under different surface roughnesses and saturated pressures

图10示出了通过模型计算得到的不同饱和压力及表面粗糙度条件下的液相毛细流动速度。通过对比可知，饱和压力对毛细流动速度作用很小，而表面粗糙度对其影响显著。由光滑表面的毛细流动流速0.66 mm/s增至粗糙度为0.587 μm表面的20.53 mm/s，即液相毛细润湿流动速度随着表面粗糙度的增加而显著增大，这有利于液相工质有效补给核化点空穴或沟槽，使沸腾表面不易形成气膜，从而提升临界热通量。

2.3 沸腾临界热通量预测及经验关联式建立

准确预测池沸腾临界热通量对于换热装置的使用安全性和可靠性至关重要，多年来学者们基于理论分析及实验数据关联建立了池沸腾临界热通量预测模型。本文将HFE-7100工质在不同饱和压力及表面粗糙度条件下的池沸腾临界热通量实验数据与表2中相关模型关联式的预测值进行了对比，以验证相关模型预测的准确性。

表2 池沸腾临界热通量预测模型关联式Table 2 Correlation formula of critical heat flux prediction model for pool boiling

HFE-7100工质在不同饱和压力及表面粗糙度条件下的池沸腾临界热通量实验值与模型关联式预测数据的对比如图11所示。对比可知，其中Guan等[16]、Bailey等[34]、Bailey等[34]、Kandlikar[21]分别对4种饱和压力条件下粗糙度为0.019、0.205、0.311、0.587 μm沸腾表面的临界热通量预测相对准确，绝对平均偏差分别为2.55%、3.74%、2.36%及2.41%。就整体而言，Bailey等[34]能相对准确地预测不同工况下的沸腾临界热通量，其平均绝对偏差为5.66%。

较多的临界热通量预测模型关联式一般通过对Kutateladze[36]定义的临界热通量无因次参数K进行修正来预测不同实验条件下的临界热通量，二者关系如式(8)所示。

(8)

上式基准项(除K外)主要反映了工质物性的影响，对于不同类型工质，在特定相同的工况下，工质的汽化潜热、气相密度、气液两相密度差及液相表面张力越大，对应的临界热通量预测值越高。同时无因次参数K通常以常数或能反映相关影响因素的无因次变量的形式来表达。表2预测模型关联式中，Guan等[16]通过引入工质气、液相密度参数，Wang等[32]引入折算压力参数，Kim等[26]引入表面粗糙度及接触角参数，Kandlikar[21]引入表面倾角及表面接触角参数，Priarone[35]引入表面倾角参数来预测临界热通量无因次参数K，而其他预测模型中选用的K为常数。

实验结果表明，系统饱和压力及沸腾表面粗糙度对稳态临界沸腾状态下的热通量有较大影响，为进一步提高预测精度，量化分析饱和压力及表面粗糙度的影响作用，可通过引入无因次参数折算压力pr与粗糙度无因次参数R来建立预测关联式。新建立的K参数经验关联式表达如下：

图11 池沸腾临界热通量实验数据与模型关联式预测值比较Fig.11 Comparison of pool boiling experimental critical heat flux and predicted value from different models

(9)

pr=pSAT/pc

(10)

R=Ra/Rsm

(11)

式中：pSAT为系统饱和压力；pc为临界压力。经验关联式应用范围：0.019 μm≤Ra≤0.587 μm；0.03≤pr≤0.09；θ<10°。

图12示出K的实验值与新建关联式及表2中模型关联式预测值的对比情况。结果表明，虽然部分模型对个别工况条件下的K预测较为准确，但本研究建立的关联式预测计算得到的K与实验值整体吻合度更高。已建模型关联式对不同工况条件下K预测的平均绝对偏差范围为5.66%～42.35%，而本文新建关联式预测平均绝对偏差为2.72%，预测精度较已建模型有明显提升。

为验证本研究建立的K预测关联式的可靠性，故将新建关联式的临界热通量预测值与已有文献实验数据进行对比。选用工质及实验条件为HFE-7100[11](实验条件：0.023 μm≤Ra≤0.6 μm，0.04≤pr≤0.09)、FC-72[16,35](实验条件：Ra=0.55 μm，pr=0.08；Ra=0.60 μm，pr=0.05)、PF-5060[37](实验条件：Ra=0.21 μm，pr=0.06)，对比结果示于图13，预测值与文献实验数据的最大绝对偏差基本在10%以内，说明本文建立的预测关联式能较好地预测特定工况下高润湿性工质的沸腾临界热通量。

3 结论

在不同表面粗糙度及饱和压力条件下，对HFE-7100工质在铜基表面的临界状态池沸腾进行了可视化及传热实验研究，分析了表面粗糙度及饱和压力对临界热通量的影响机制，对比了相关预测模型的准确性，并新建了K预测关联式，得到以下结论。

1) 临界状态下的沸腾两相工质通常由气泡、蒸气柱及蘑菇状气团组成，气液两相运动过程剧烈，形态更为多样化；过渡状态下非平整气膜覆盖于沸腾表面，气泡以分散状态不断从气膜中脱离，过程形态相对单一。

2) 沸腾表面粗糙度及系统饱和压力均对稳态临界状态下的池沸腾传热通量产生积极的提升作用。本实验工况下，最大提升比率为76%。机理分析表明，系统饱和压力的改变会影响气泡水平方向扩增力、液相边界层厚度及恢复周期；而表面粗糙度的变化会引起液相工质在沸腾表面的铺展润湿动态过程发生改变。

图12 池沸腾K实验值与模型关联式预测值比较Fig.12 Comparison of pool boiling experimental K and predicted value from different models

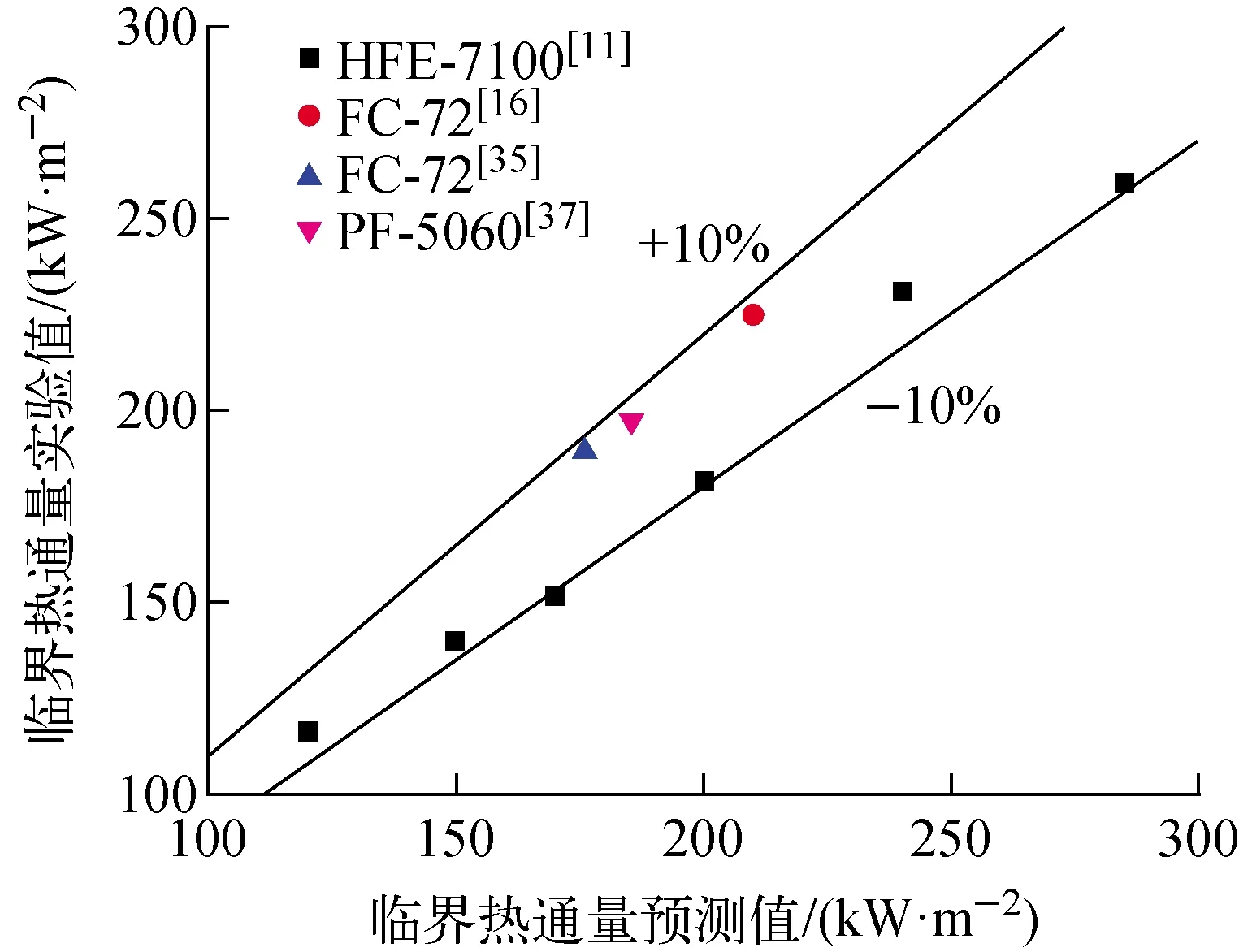
图13 文献临界热通量实验数据 与新建关联式的预测值比较Fig.13 Comparison of CHF experimental data from other literature and predicted value from new model established in this study

3) 相较其他临界热通量预测模型关联式而言，Bailey等能较准确地预测不同表面粗糙度及饱和压力条件下的沸腾临界热通量，其平均绝对偏差为5.66%。为提升临界热通量关联式预测精度，本文通过引入代表饱和压力及表面粗糙度的无因次参数建立了K预测关联式，预测值与本研究及文献实验数据吻合较好。