一种快速搜索临界棒位方法的开发与评价

李治刚，安 萍，严明宇,2，刘 东,3,*，芦 韡，余红星,2

(1.中国核动力研究设计院，四川 成都 610041；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041；3.中核集团核能软件与数字化反应堆工程技术研究中心，四川 成都 610041)

目前，堆芯物理设计与计算通常采用两步法[1]，组件计算程序生成组件库，堆芯程序基于组件库进行全堆芯计算。反应性控制[2-3]是堆芯核设计的重要内容，硼溶液、控制棒等是控制堆芯反应性的重要手段。以钠冷快堆[4-5]为代表的金属冷却反应堆主要采用控制棒实现堆芯反应性控制，计算临界棒位是金属冷却快堆物理设计中的必要内容。

在非确定论程序中，传统的临界搜索方法需通过多次临界计算，具有计算量大、临界结果不准确等缺点，一些研究机构提出了基于微扰计算的蒙特卡罗临界搜索方法[6-7]以克服上述缺点。而在确定论程序中，目前常采用线性插值或线性外推[8]的方法获得堆芯临界棒位，由于控制棒的价值与控制棒插入堆芯深度并不呈简单的线性关系[9]，通过线性插值方法往往需多次迭代计算控制棒棒位才能使堆芯达到临界，计算效率较低。特别针对金属冷却快堆换料周期较长的特点，要完成整个寿期的调棒临界计算需3～5 d，不利于堆芯设计方案的设计和优化。

为克服调棒临界线性插值方法迭代次数多的缺点，提高临界搜索效率，本文提出一种基于控制棒价值函数的临界棒位快速搜索方法，并将该方法在堆芯三维中子学物理程序PBRT[10]中予以开发。对控制棒价值函数法涉及的理论及计算流程进行描述，并基于一种典型的金属冷却快堆堆芯布置对其进行测试，以验证该方法的可行性和准确性。

1 理论模型

采用控制棒搜索临界的一般计算流程如图1所示，线性插值法和控制棒价值函数法在临界棒位搜索环节有所差异。前者采用线性插值获得新的临界棒位，而后者通过内置预先得到的控制棒棒位与有效增殖因数keff的函数关系，直接计算得到新的临界棒位。

1.1 线性插值法

假设堆芯有N组控制棒，控制棒组编号为1～N，控制棒组初始棒位H0(本文棒位均指距离堆芯底部的高度)，第i次迭代计算时的控制棒组棒位为Hi，堆芯临界有效增殖因数为keff,critical，堆芯临界收敛准则ε，不考虑控制棒组叠步运动。则第i次迭代后采用线性插值计算得到的新棒位Hi+1[11]为：

(1)

式中：keff,H0和keff,Hi分别为控制棒组位于初始棒位H0和Hi时的堆芯有效增殖因数。

图1 控制棒搜索临界计算流程Fig.1 Control rod critical computing flow

1.2 控制棒价值函数法

由于控制棒价值[12]与控制棒插入深度不呈线性关系，采用线性插值往往需多次迭代才能搜索到堆芯临界的控制棒棒位。若能较为准确地得到控制棒价值与控制棒组棒位的函数关系，则可直接计算得到满足临界收敛准则的控制棒棒位。控制棒价值函数法的计算流程如图2所示。

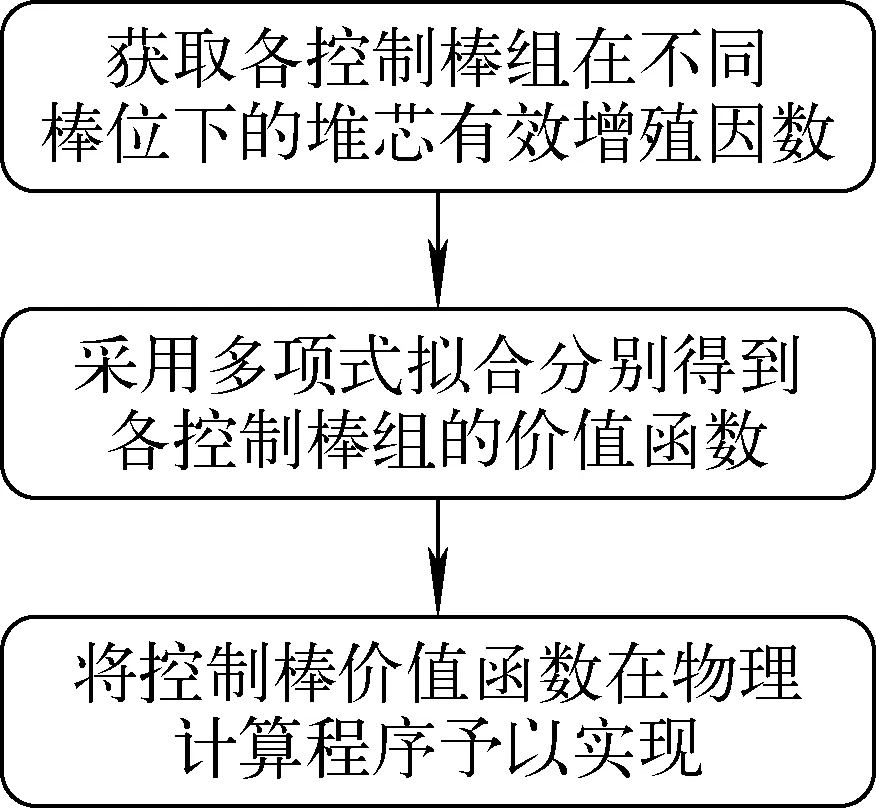
图2 控制棒价值函数法计算流程Fig.2 Calculation flow of control rod value function method

Δki=keff,z(i)-keff,z(i-1)

(2)

(3)

式中：keff,z(i)和keff,z(i-1)分别为控制棒组位于z(i)和z(i-1)处堆芯的有效增殖因数；keff,bottom为控制棒组位于堆芯底部时堆芯的有效增殖因数。

假设第i组控制棒积分价值与控制棒组棒位的关系为y(i)=f(z(i))，第i组控制棒移动Δz(i)时的keff为：

keff=keff,z(i)+fi(z(i)+Δz(i))-fi(z(i))

(4)

考虑N组控制棒移动时的keff为：

keff=keff,(z(1),z(2),…,z(N))+

(5)

根据调棒顺序，逐步提出控制棒组，直到堆芯keff满足临界收敛准则，并记录此时各控制棒组的棒位z(i)(i=1,…,N)，即为临界棒位。

采用最小二乘法曲线拟合[13]或切比雪夫(Chebyshev)[14-15]曲线拟合多项式拟合的方法获取控制棒组积分价值与控制棒组棒位的函数关系fi(z(i))。

2 测试与验证

将控制棒价值函数法应用到堆芯三维中子学程序PBRT的调棒临界搜索模块中，并以金属冷却快堆典型六边形堆芯布置来验证该方法在实现快速搜索临界棒位的可行性。在堆芯中布置有3种不同价值的控制棒组，编号为1、2、3。假设共计算10个燃耗步，每个燃耗步步长为100满功率天。

1) 控制棒组价值

采用PBRT计算得到寿期初、寿期末3组控制棒分别单独提出堆芯的keff。图3示出了3组控制棒微分价值和积分价值随控制棒组棒位的变化。从图3可看出控制棒组提出微分价值随控制棒组的提出呈抛物线趋势变化，在接近堆芯活性区中部位置时，引入的keff变化幅度达到最大；控制棒组提出积分价值随控制棒组的提出呈近似S形曲线变化。提出微分价值和提出积分价值在寿期初至寿期末的变化幅度较小，因此在控制棒价值函数方法实现过程中，可假定控制棒价值在整个寿期(寿期较短)保持不变。

采用最小二乘法多项式拟合方法和切比雪夫最佳拟合方法获得各组控制棒提出积分价值与控制棒组棒位的函数关系。图4示出了两种拟合方法对1号棒组的拟合结果，其他棒组的拟合规律与之基本类似。从图4可看出，拟合阶数越低，拟合函数与真实结果偏差越大；5阶时，最小二乘法拟合结果优于切比雪夫法；10阶时，两种拟合方法与真实结果完全重合为S形曲线。 2) 临界棒位搜索

将最小二乘法拟合的控制棒价值函数应用到堆芯物理设计程序的调棒临界搜索模块中，临界搜索收敛准则为ε=0.001。图5示出了控制棒价值函数法与线性插值法在第2个燃耗步时搜索临界过程中keff的变化。控制棒价值函数法仅进行了1次迭代计算便搜索到了临界棒位；而线性插值法需要15次迭代插值计算才满足临界收敛准则。

图3 3组控制棒微分价值和积分价值随棒位的变化Fig.3 Differential value and integral value of three sets of control rods vs. rod position

图4 1号棒组提出积分价值函数与拟合阶数的关系Fig.4 Raising integral value function of No.1 rod vs. fitting order

图5 第2个燃耗步调棒临界搜索过程keff变化Fig.5 keff change during process of searching critical rod position in the second burnup step

图6示出了两种方法计算的第2～10个燃耗步的临界棒位和对应的keff。图5中显示的为2号棒组的棒位，在第2至10个燃耗步过程中，1号棒组已完全提出堆芯，3号棒组仍全部插入。从图6可看出，两种方法计算得到的临界棒位的数值及趋势基本一致，除第3个燃耗步时两种方法的计算偏差超过4%，其他各点偏差均在2%范围内。采用线性插值法和控制棒价值函数法计算得到的keff均在临界搜索收敛准则范围内。

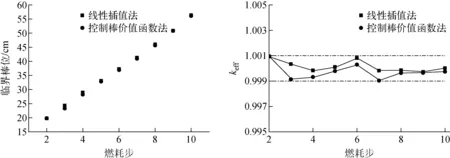
图6 临界棒位和keff随燃耗步的变化Fig.6 Critical rod position and keff vs. burnup step

3) 计算效率

图7示出了单个燃耗步的计算时间以及燃耗步的累计计算时间。采用线性插值法的第1次调棒临界搜索计算时间较长，后续燃耗步的计算时间基本维持在约1 h。而采用控制棒价值函数法后续燃耗步的计算时间基本维持在约0.5 h。从图7可看出，完成10个燃耗步计算，采用控制棒价值函数法的累计计算时间较采用线性插值法的缩短了1倍，计算效率明显提高。

3 结论

由于采用线性插值法进行调棒搜索临界需要多次迭代计算、效率低，本文提出了一种基于控制棒价值函数的快速调棒搜索临界方法，对该方法的理论及计算流程进行了阐述，并在堆芯物理设计程序中进行了应用和初步验证，得出如下结论。

1) 与线性插值法相比，采用控制棒价值函数法仅进行1次迭代计算即可搜索到临界棒位，满足临界搜索收敛准则，搜索效率明显提高。

图7 单个燃耗步的计算时间以及燃耗步的累计计算时间Fig.7 Computation time of single burnup step and cumulative computation time of all burnup steps

2) 采用控制棒价值函数法，燃耗计算时间缩短了约1倍，有助于提高堆芯物理设计的效率。

3) 通过增加计算控制棒价值的数据点和提高多项式拟合的阶数，可提高控制棒价值函数法的准确度。

本文提出的控制棒价值函数法为堆芯物理设计和优化降低了计算时间，是一种合理可行的快速搜索临界棒位方法，有效克服了传统线性插值方法中的不足。