典型压水堆堆芯物理-热工耦合稳态计算软件的开发与验证

李治刚，安 萍，潘俊杰，卢 川，芦 韡,*，杨洪润

(1.中国核动力研究设计院，四川 成都 610213； 2.核反应堆系统设计技术重点实验室，四川 成都 610213)

在压水堆中燃料温度、慢化剂密度、冷却剂温度等热工参数会影响中子的截面，进而影响堆芯中子通量和功率分布，而功率又反过来影响堆芯燃料温度、冷却剂温度等热工参数，即压水堆中子物理与热工之间存在强烈的反馈现象[1]，因此目前在压水堆的设计和安全分析中均须考虑物理-热工耦合计算，以便更加真实地模拟堆芯稳态和瞬态过程。自20世纪80年代以来，国内外针对压水堆物理-热工耦合现象开展了大量研究，提出了较多有效的耦合计算方法，如Picard迭代法[2]、JFNK迭代法[3]，并研发了大量三维物理-热工耦合计算软件，如CRONOS/FLICA4、PARCS/TRACE[4]、CSSS[5]、DYN3D/ATHLET[6]、NALSANMT/CORBA-Ⅳ[7]等。

目前典型的堆芯物理-热工耦合计算程序常采用外耦合方式实现，且常采用1种中子物理或热工水力计算方法求解守恒方程。为研究不同中子物理、热工水力计算方法对压水堆物理-热工耦合计算的影响，本文通过内耦合方式实现物理-热工耦合计算，研制典型压水堆堆芯物理-热工耦合计算软件ARMcc，其中采用节块展开法(NEM)[8]和格林函数节块法(NGFM)[9]求解中子扩散方程，分别采用单通道计算模型[10]和一维圆柱导热计算[11](采用有限差分法或有限体积法求解)冷却剂温度和燃料温度，并采用典型压水堆耦合基准题NEACRP[12-13]弹棒初始参数对软件稳态计算功能进行验证。

1 理论模型

1.1 稳态中子扩散方程求解方法

多群稳态中子扩散方程[14-15]可表达为：

(1)

式中：χg为裂变谱；Dg为第g群中子扩散系数；Σfg′为第g′群裂变宏观截面；φg为第g群中子注量率；υg′为第g′群平均裂变中子数；Σsg′→g为第g′群到第g群的散射截面；ΣRg为第g群的移除截面；k为特征值或有效增殖因数。

目前式(1)的典型求解方法包括有限差分法、节块法、有限元方法等，其中节块法由于具有较高的效率和精度，在商业软件中被广泛应用。节块法的重要特点是对式(1)进行横向积分，将三维问题的求解变成联立求解3个一维问题。在网格m内，对给定的坐标方法u(交替等于x,y,z)，对式(1)沿与u方向垂直的另两个方向v和w进行积分，得到3个一维方程(为便于描述，全文略去节块编号m)：

g=1,…,G;u=x,y,z;u≠v≠w

(2)

式中，φgu、Qgu和Lgu分别为横向积分通量、源项(包括裂变源项和散射源项)和横向泄漏项。

典型的节块法有NEM、解析节块法(ANM)和NGFM等，不同节块法的差异在于φgu、Qgu和Lgu等近似处理方式。本文将采用四阶NEM和第二类边界条件NGFM进行多群稳态中子扩散方程的求解，具体的理论详见文献[8-9]。

1.2 热工水力计算方法

1) 单通道计算模型

冷却剂单相单通道的守恒方程为：

(3)

式中：ρ为冷却剂密度，kg/m3；h为冷却剂焓，J/kg；u为冷却剂流动速度，m/s；q为体积热流密度，W/m3。

对式(3)在网格m进行z方向的积分得到：

(4)

根据入口边界条件，采用式(4)可依次计算得到每个网格出口焓hout，则网格m的平均焓为:

(5)

2) 一维圆柱导热模型

一维圆柱导热稳态模型的守恒方程为：

(6)

式中：λ为导热系数，W/(cm·℃-1)；T为温度，℃。

典型的压水堆燃料元件几何形式如图1所示。在径向上燃料芯体划分为n个网格，气隙为1个网格，包壳划分为2个网格。

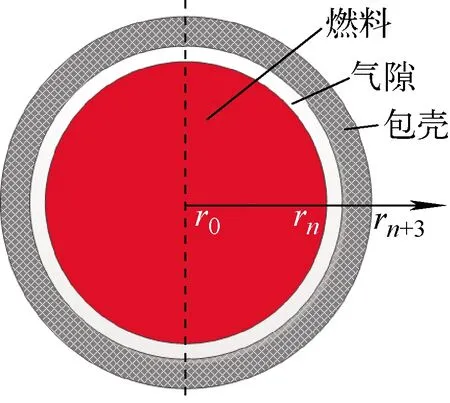
图1 典型压水堆燃料元件几何形式Fig.1 Geometry of fuel element in typical PWR

(1) 有限差分法

采用有限差分法(DIF)对式(6)在网格i处进行离散，得到网格i的温度计算关系式：

(7)

式中：λ为材料的导热系数；ri为第i个网格的半径；Δri为第i个网格的间距。关于燃料中心、芯体外表面、包壳内外表面的处理方式参见文献[16]。

(2) 有限体积法

采用有限体积法对式(6)进行离散，表达形式如下：

(λi-1/2ri-1/2+λi+1/2ri+1/2)·

(8)

式中，ri+1/2和ri-1/2分别为第i个网格左右边界的半径。

式(7)、(8)均为三对角矩阵，采用高斯-赛德尔迭代计算得到燃料元件的径向温度分布，采用罗兰公式加权计算燃料有效温度。

2 验证与分析

基于上述中子物理和热工水力计算理论，采用C/C++语言开发了反应堆堆芯多物理耦合计算软件(ARMcc)。本文分别采用三维LWR基准题[17]和NEACRP-L-335基准题[12-13,18]对程序中子扩散方程求解和物理-热工耦合计算进行验证。

2.1 中子扩散方程求解验证

三维LWR基准题的几何布置及材料截面参数见文献[17]。采用NEM和NGFM对三维LWR基准题进行模拟，堆芯有效增殖因数keff结果及偏差列于表1，三维LWR基准题相对功率分布及偏差如图2所示。

表1 keff结果及偏差Table 1 Result and deviation of keff

由表1和图2可知，本软件采用的NEM和NGFM方法模拟三维LWR基准题均具有较高的精度。keff与参考结果相比，NEM和NGFM方法计算的keff偏差均在10 pcm以内；堆芯径向相对功率与参考结果相比，采用NEM方法的最大偏差为0.553%，采用NGFM方法的最大偏差为1.03%。

图2 三维LWR基准题相对功率分布及偏差Fig.2 Relative power distribution and deviation of 3D LWR benchmark

2.2 物理-热工耦合计算验证

图3 PWR NEACRP弹棒基准题堆芯模型Fig.3 Core model of PWR NEACRP rod ejection benchmark

NEACRP弹棒基准题是1991年由Finnemann等[12-13]建立的，包含压水堆和沸水堆两种堆型，主要用于轻水堆堆芯三维物理-热工耦合软件的验证。其中压水堆基准题参考了典型压水堆的几何尺寸和运行状态，堆芯布置了157个燃料组件和1圈径向反射层，轴向分为18层，如图3所示[18]。根据初始功率水平和控制棒弹出位置的不同，共包含6种工况：A1，1/4堆芯、中心控制棒在热态零功率(HZP)弹出；A2，1/4堆芯、中心控制棒在热态满功率(HFP)弹出；B1，1/4堆芯、外围1组控制棒在热态零功率弹出；B2，1/4堆芯、外围1组控制棒在热态满功率弹出；C1，1/2堆芯、外围1组控制棒在热态零功率弹出；C2，1/2堆芯、外围1组控制棒在热态满功率弹出。

关于NEACRP基准题几何尺寸划分及材料截面参数可详见文献[12]，基准题的参考结果由PANTHER程序采用精细时空网格计算，在1993年发布初版、1997年发布修订版，计算结果包括稳态和瞬态关键结果参数。本文将采用1997年修订版的稳态计算结果对本软件物理-热工稳态耦合计算模块进行验证，而对于PANTHER未提供的结果参数(如堆芯组件径向功率分布等)将采用PARCS软件计算结果作为参考。2种物理计算方法和2种热工计算方法组合后形成4种计算模式(NEM+VOL对应节块展开法和有限体积法，NEM+DIF对应节块展开法和有限差分法，NGFM+VOL对应格林函数法和有限体积法，NGFM+DIF对应格林函数法和有限差分法)。

1) 临界硼浓度

采用ARMcc针对NEACRP基准题计算的临界硼浓度对比结果列于表2。与PANTHER(1997)相比，4种模式计算的6种工况的临界硼浓度与参考结果符合较好，最大相对偏差在0.5%以内，其中在A2和C2工况中，NEM方法计算临界硼浓度的精度高于NGFM方法，而在剩余4个工况中，NGFM方法计算临界硼浓度的精度高于NEM方法。

2) 堆芯组件径向相对功率最大值

径向相对功率最大值Fxy,max列于表3。与PARCS结果相比，ARMcc计算的堆芯组件径向相对功率最大值与参考结果符合较好，相对偏差在0.5%以内。采用NEM方法计算的最大相对偏差-0.39%出现在A2算例中，而采用NGFM方法计算的最大相对偏差0.27%出现在C2算例中。采用有限体积法或有限差分法对Fxy,max的影响较小。

B1算例堆芯组件径向功率分布如图4所示，其中在同一种物理方法中采用VOL和DIF的相对功率分布基本相同。从图4可知，相对功率<0.9的组件功率最大偏差情况为：NEM方法为2.09%，NGFM方法为-0.14%，相对功率>0.9的组件功率最大相对偏差情况为：NEM方法为-1.48%，NGFM方法为-0.06%。

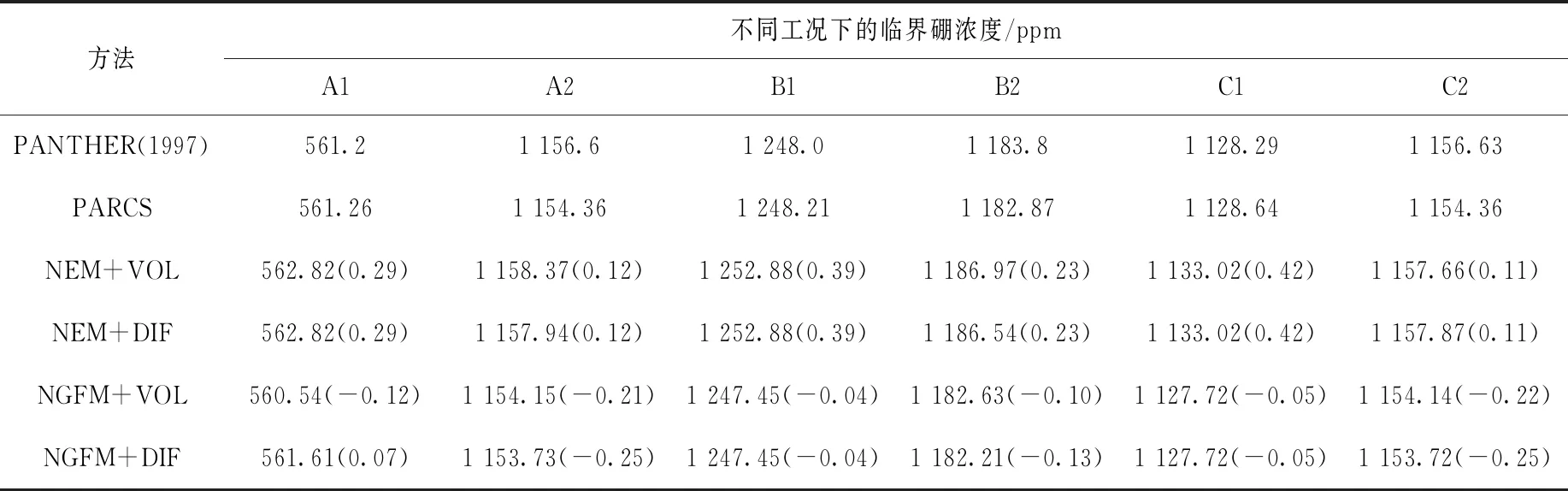
表2 不同工况下的临界硼浓度Table 2 Critical boron concentration of different cases

表3 不同工况下的堆芯组件径向相对功率最大值Table 3 Maximum radial relative power of core assembly of different cases

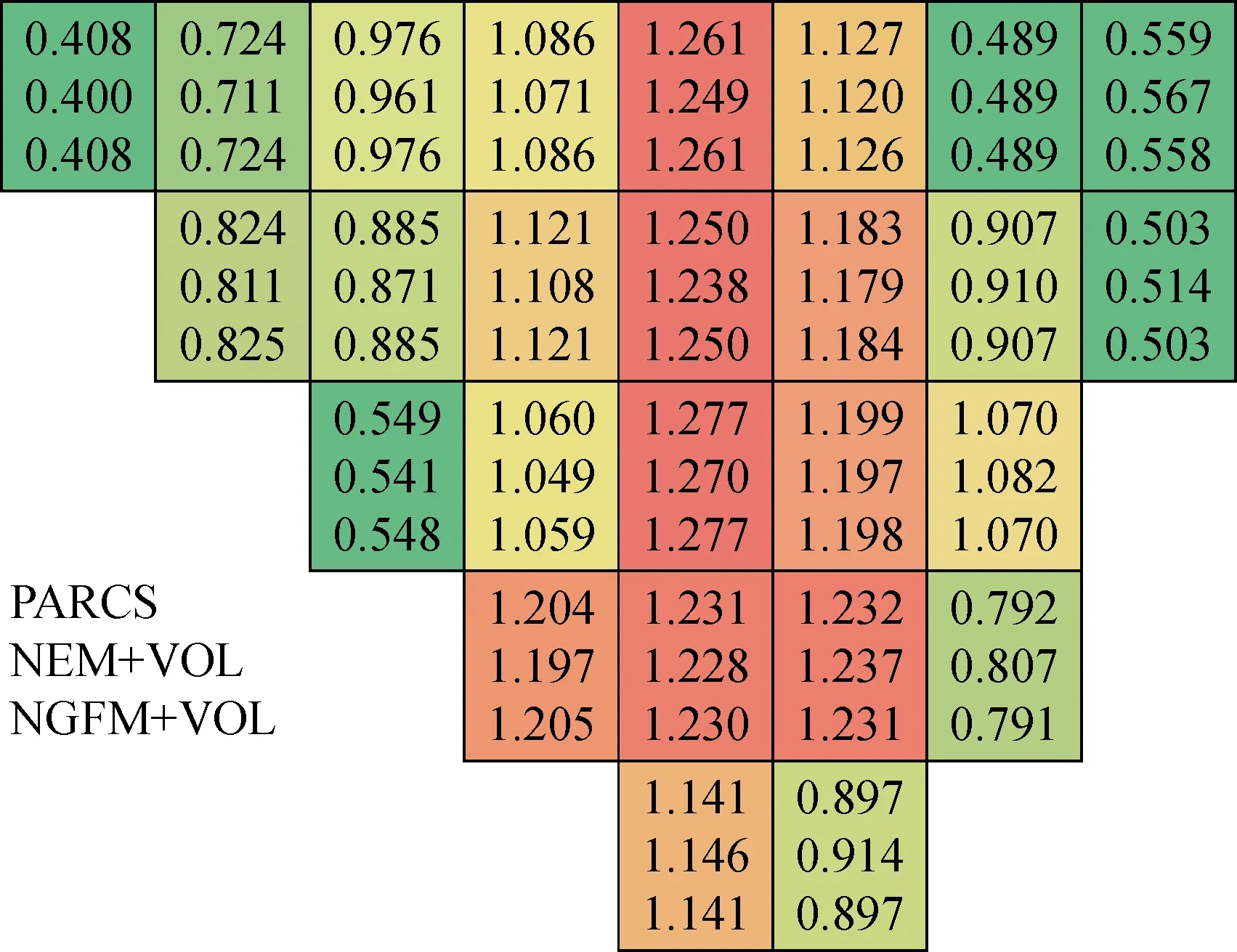
图4 B1算例堆芯组件径向功率分布(1/8堆芯)Fig.4 Radical power distribution of B1 case (1/8 core)

3) 堆芯轴向相对功率最大值

堆芯轴向相对功率峰值Fz,max列于表4。与PARCS结果相比，4种计算模式得到的堆芯轴向相对功率最大值与参考结果符合较好，最大相对偏差不超过0.1%。采用NEM+VOL模式计算时在满功率工况A2、B2和C2中相对偏差达到最大，为0.1%。

4) 堆芯燃料最高温度

表5列出不同工况下的堆芯燃料最高温度。与PARCS结果相比，因零功率算例(A1、B1和C1)堆芯功率较小，燃料最高温度与初始温度相同，相对偏差为0.0%；在满功率算例中，不同计算模式得到的燃料最高温度存在明显差异：1) 采用相同物理计算方法时，采用有限体积法得到的燃料最高温度低于采用有限差分法；2) 采用相同热工计算方法时，NEM方法计算的结果低于NGFM方法；3) NEM+VOL模式相对偏差最小(B2算例中为0.77%)，NGFM+DIF模式相对偏差最大(C2算例中为1.33%)。

表4 不同工况下的堆芯轴向相对功率峰值Table 4 Core axial relative power peak of different cases

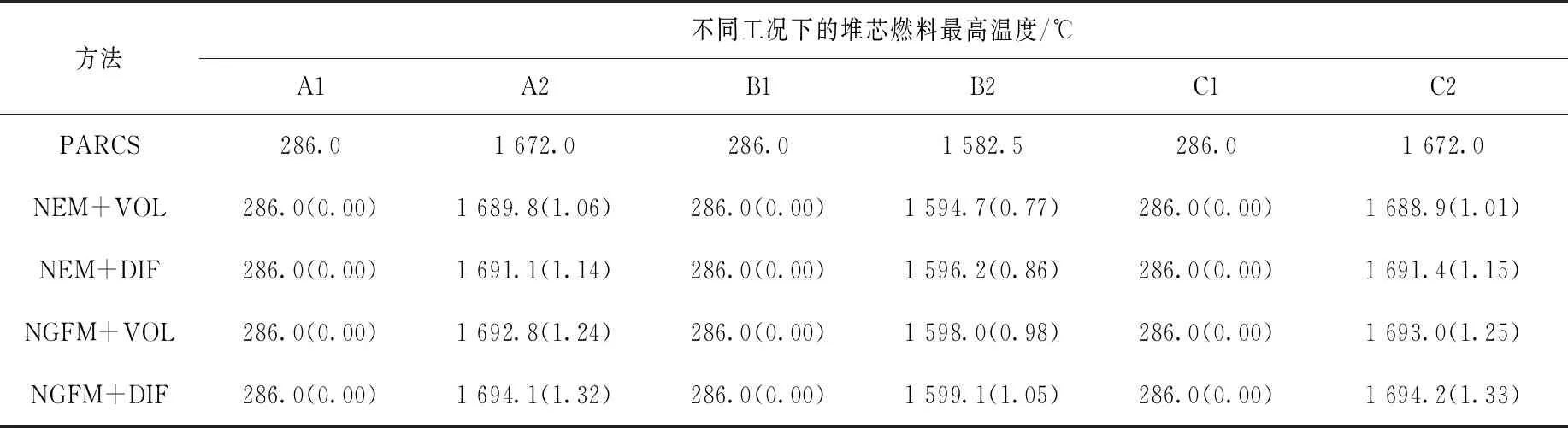
表5 不同工况下的堆芯燃料最高温度Table 5 Core maximum fuel temperature of different cases

5) 堆芯燃料多普勒温度

堆芯燃料多普勒温度影响中子截面参数，表6列出不同工况下的堆芯燃料多普勒温度。与PARCS结果相比，零功率算例相对偏差为0.00%；在满功率算例中，4种计算模式的最大相对偏差在0.5%以内，有限差分法较有限体积法更接近参考结果。

6) 堆芯出口冷却剂最高温度

堆芯出口温度体现了热量在轴向上的积分效果。堆芯出口冷却剂最高温度列于表7。与PARCS结果相比，零功率算例相对偏差为0.00%；在满功率算例中，4种计算模式的最大相对偏差在0.2%以内，而NGFM方法的相对偏差小于NEM方法的，更接近参考结果。

表6 不同工况下的燃料多普勒温度Table 6 Core fuel Doppler temperature of different cases

表7 不同工况下的堆芯出口冷却剂最高温度Table 7 Maximum temperature for core coolant outlet temperature of different cases

3 结论

本文针对压水堆堆芯物理-热工耦合计算现象，基于2种典型节块法和一维圆柱导热计算方法，研制了堆芯物理-热工耦合稳态计算程序，采用三维LWR基准题对中子物理求解模块进行了验证，采用LWR弹棒基准题NEACRP-L-335的稳态结果对物理-热工耦合稳态计算模块进行了验证，分析了中子物理、热工水力计算方法对物理-热工耦合计算的影响，得到如下结论。

1) 采用NEM方法和NGFM方法在求解中子扩散方程时具有良好的精度，对三维LWR基准题模拟结果与参考结果符合较好。

2) 4种计算模式均能较为准确地模拟堆芯物理-热工耦合过程，但不同计算模式对关键参数的影响程度不同：对堆芯出口温度和堆芯轴向相对功率最大值的影响较小，对堆芯临界硼浓度、堆芯燃料最高温度和堆芯多普勒温度影响较大。

3) NGFM+DIF模式能更加准确地模拟堆芯燃料多普勒温度和堆芯功率分布；NGFM+VOL模式能更加准确地模拟临界硼浓度；NEM+VOL能更加准确地模拟堆芯燃料最高温度。