基于标志点的多相机数字图像相关方法精度分析及土木工程中的应用
2021-04-20董志强邵新星何小元
魏 康 员 方 董志强 邵新星 吴 刚 何小元
(东南大学土木工程学院, 南京 210096)
数字图像相关(digital image correlation,DIC)方法由Peters等[1]在1982年最早提出,该方法因其非接触、全场测量、适用范围广等特点在科研和工程领域得到广泛关注[2-4].经过近几十年硬件的快速发展,以及匹配算法[5-7]、标定方法[8-9]、测量精度[10-11]等方面的大量研究,目前三维DIC方法已被广泛应用于土木工程、航空航天、生物医学等领域的表面三维形貌和变形测量.但在土木工程领域,被测对象通常具有结构尺寸大、柱式构件表面曲率大的特点,此时由常规双相机组成的三维DIC测量系统已不能满足实际测量需求.
为此,学者们在双相机测量系统的基础上提出多相机三维DIC测量方法,其中多相机指的是3个或更多的相机[12].实现多相机测量的关键是相机外参的标定.相机外参的标定方式决定了多相机测量方法应用过程的简便性(如基于重叠视场实现外参标定的方法,需要相机两两之间连续标定,相机数量较多时标定步骤繁琐费时)和实际场景应用中的简便性(如基于经纬仪等大量程测量设备进行外参标定的方法,需要相机之间利用设备互相观测,无法用于狭小或有遮挡的测量环境),而且相机外参的标定精度会直接影响测量结果的准确性.针对多相机外参标定,学者们做了许多研究工作[12-24],其中相机内参的标定可在实验室内提前完成.
多相机三维DIC测量方法的外参标定大致可以分为2类.第1类是基于重叠视场[12-15]外参标定方法,该方法借助重叠视场完成多相机系统测量数据的拼接,其实现需要各相机两两之间存在1/3~1/2左右的重叠区域用以标定和计算.该方法除了布置方式受限(要求各相机视场必须连续)、相机测量视场不能得到充分利用之外,相机之间的测量结果互相关联,测量系统稳定性差.第2类是无需重叠视场实现外参标定的多相机方法,其主要可以归为以下几种类型:利用经纬仪或激光跟踪仪等大量程测量设备[16-19]实现全局标定的方法;通过追踪目标的运动模型[20-22]来建立不同相机视场间对应关系的方法;利用大规模标定物[23-24]进行标定的方法;基于标志点重构[25-26]的外参统一方法.其中,基于标志点重构的外参统一的多相机方法具有操作简便、相机可灵活布置、各子相机系统之间基本互相独立、测量结果稳定性高的优点.
因此,本文首先设计基于标志点的多相机三维DIC方法的精度验证实验,对该方法的可行性和精度进行了验证.通过寻找不同测量系统在重叠区域下测量点的对应关系,利用对应点拼接误差un的均值和标准差来评估多相机数据统一的精度.平移验证实验表明,经坐标统一后的多套测量结果对应良好.最后,将该方法用于玄武岩纤维增强树脂基复合(basalt fiber-reinforced polymer, BFRP)筋海水海砂珊-超高性能混凝土(ultrahigh-performance concrete, UHCP)组合梁的抗弯承载实验,得到破坏临界荷载下的全场位移和应变云图,并与位移计数据进行对比分析,结果显示本文使用的基于标志点的多相机测量方法操作简便、布置灵活,能精确地测量混凝土梁的表面位移.
1 基于标志点重构的多相机三维DIC系统测量原理
为实现不同坐标系下多相机系统的数据统一,使用多套独立的三维DIC测量子系统和一台单反相机构成一套多相机三维DIC测量系统,其中三维DIC测量子系统的相机内、外参由标定板获得,而测量子系统之间的相对外参则借助标志点获得.由于基于标志点的多相机测量方法无需借助重叠区域,因此可以根据测量需求和环境限制对相机系统进行灵活布置,工程适用场景广泛.
1.1 三维DIC测量原理
三维DIC测量系统主要由2个工业相机和采集设备组成,利用双目立体视觉原理和图像相关匹配技术实现位移和应变的计算.首先使用2台相机从不同方位同时对一目标进行拍摄,将拍摄到的二维图像进行特征匹配处理,从而寻找到各点的对应关系,再根据标定得到的两相机参数,即可利用立体视觉原理计算出每个点在定义坐标系下的三维坐标.双目视觉原理如图1所示,对于世界坐标系Ow-xwywzw下任意待测点P,该点分别成像于左、右相机A、B像平面坐标系Oi1-xi1yi1和Oi2-xi2yi2的P1、P2处,由于P、P1、P2三点共面,可计算出点P的三维坐标(X,Y,Z)w,其中P1、P2坐标可由标定和图像匹配计算得到,而Oc1、Oc2分别为左、右两相机坐标系Oc1-xc1yc1和Oc2-xc2yc2的光心.图像相关匹配技术则包括同一时刻2幅图的散斑之间和同一相机图片中散斑变形前后的匹配,即立体匹配和时序匹配,利用形函数和相关函数寻找同一点在不同图像下的对应关系.
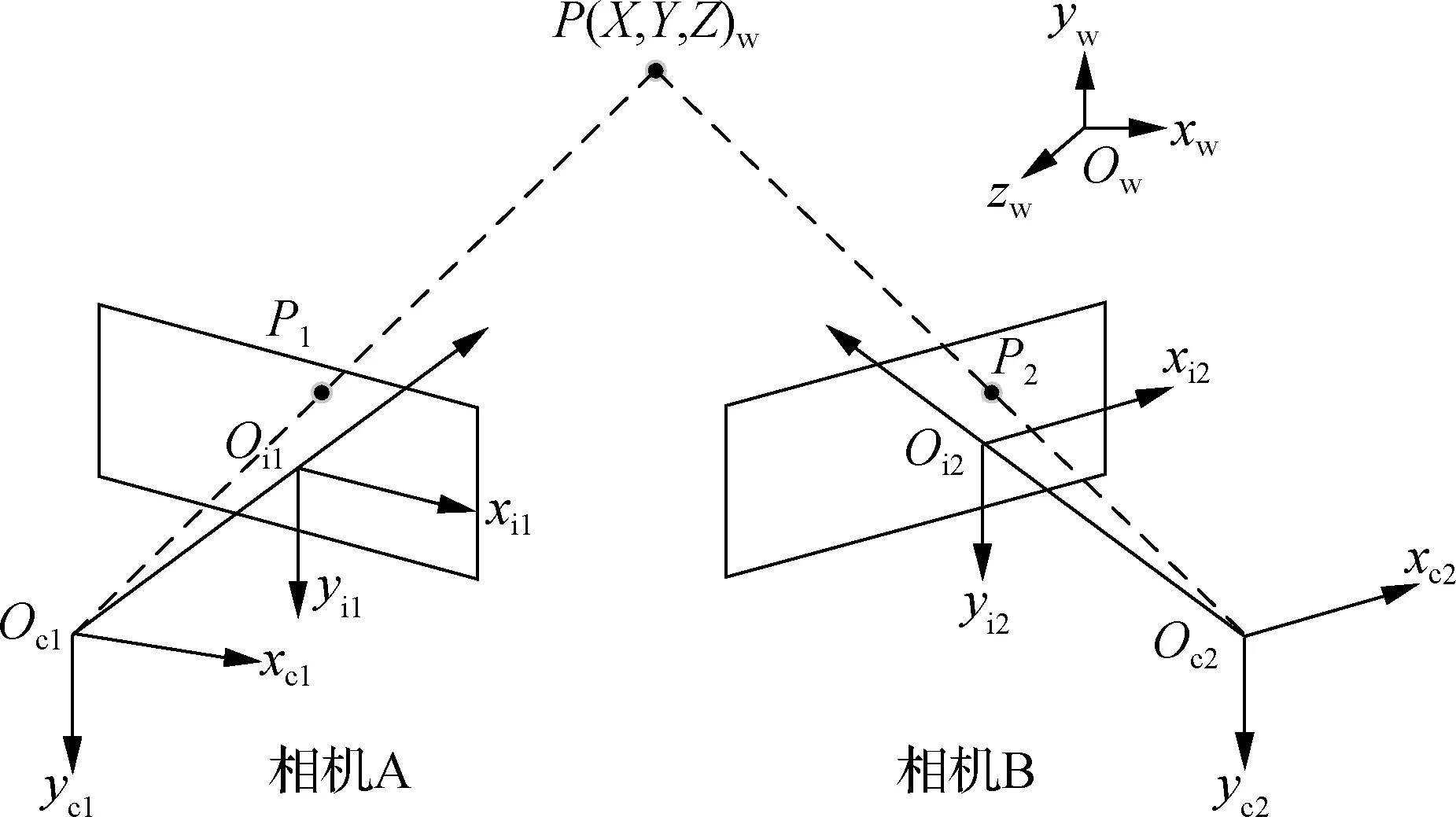
图1 双目立体视觉原理
1.2 单相机近景摄影测量
对于标志点三维坐标的重构主要基于近景摄影测量技术[27-28]来实现,即利用不同位置不同角度拍摄得到的多张贴有编码标志点的被测物体图片,使用数字图像处理和摄影测量技术处理,进而精确测定目标在三维空间中位置的方法.由便携式单反相机拍摄得到的一系列图片用于重构标志点的三维坐标,借此可以标定各子系统的相对外参,从而得到坐标转换后相同坐标系下完整的全场三维数据.本文中使用的圆环形编码标志点编码原理如图2所示,编码采用顺时针的15位二进制数,黑色为0,白色为1,可以任意位置作为起点读数,选择对应最小十进制数值作为编码值以保证编码的唯一性.本文使用长度已知、热膨胀系数较小的高精度碳纤维刚性标尺进行尺度标定.
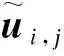
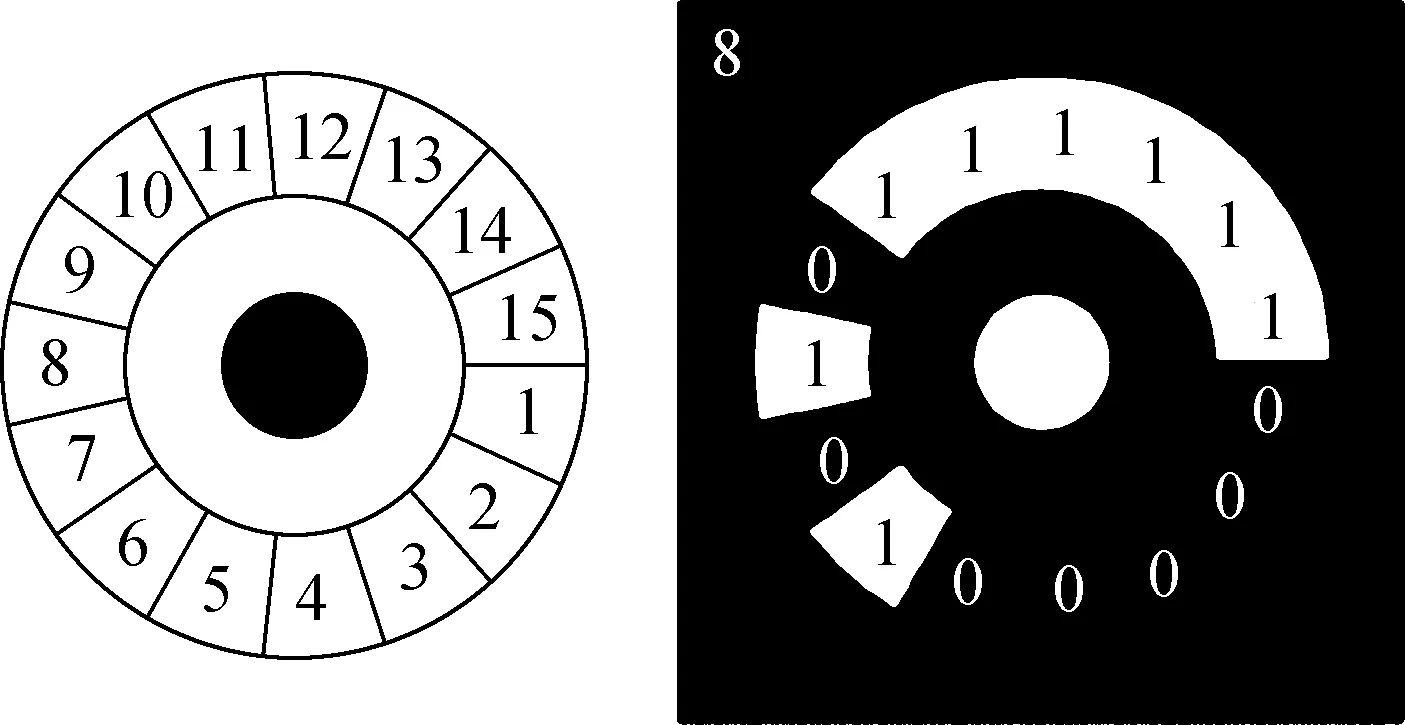
图2 同心圆环形编码标志点原理图
(1)
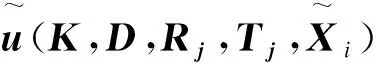
1.3 多相机数据统一
由三维DIC测量子系统可以得到标志点在各自坐标系Ocm-xcmycmzcm(m=1,2,…,s;s≥2)下的三维坐标,将世界坐标系定在单反相机坐标系并计算全部标志点的三维坐标,通过编码值相同的对应关系可计算不同坐标系的刚性转置信息,实现测量数据统一,原理如图3所示.
该过程实质为一个最小二乘求优问题,用公式可描述为
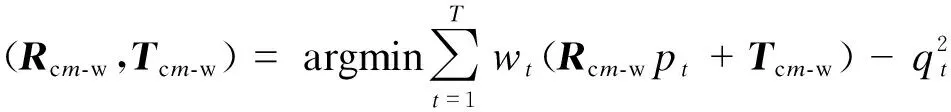
(2)
式中,m为DIC子系统序号;t、T分别表示第m个DIC子系统识得的标志点序号和总数;wt>0为点集中各点对的权重;pt和qt分别为不同坐标系下的对应点;Rcm-w,Tcm-w为子系统坐标系转到世界坐标系的旋转与平移矩阵.
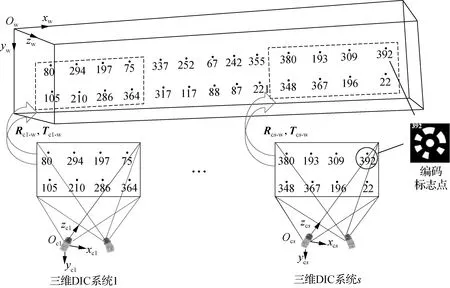
图3 多相机系统坐标统一原理图
2 精度验证
2.1 评估原理
为实现多相机三维DIC系统测量结果的定量评估和误差分析,建立重叠区域内三维形貌数据的对应关系,以对应数据差值绝对值的均值和标准差来评估误差.以2套三维DIC系统为例,对应关系的建立具体如下:①将点集1中在(x,y)i1处的测量值记为D(1)(x,y)i1,利用相机内、外参转换到点集2的像素坐标系下变为D(1)(x′,y′)i2,搜索该点在点集2中距离最近的整像素点D(2)(X,Y)i2,完成初始对应;②为保证对应精度,将点集1中实现初始对应的点取k×k(k可取3、4或5)的非线性拟合窗口,得到测量值D(1)(x′,y′)i2在点集2的亚像素对应D(2)(x′,y′)i2.建立好精确的对应关系后,对点集1和点集2的测量值进行误差分析.
用于评估数据坐标统一精度的均值和标准偏差公式分别为
(3)
(4)
其中
un=|D(1)(x′n,y′n)-D(2)(x′n,y′n)|
(5)
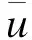
D(2)(x′n,y′n)=a0+a1x′n+a2y′n+a3(x′n)2+
a4x′ny′n+a5(y′n)2
(6)
式中,a0,a1,…,a5为拟合参数.
2.2 验证实验
为证明本文多相机三维DIC测量方法的可行性和有效性,进行散斑平面平移验证实验,实验方案布置图如图4所示.使用4个相机组成2套三维DIC测量系统,为了避免测量结果引入其他因素的影响,采用相同相机型号和镜头焦距,实验初始保证4个相机的视场中心均对准待测散斑平面中心,并将2套测量系统对称布置.其中,待测平面的散斑区域尺寸为300 mm×300 mm,调节镜头焦距和光圈至被测平面表面清晰成像,清晰成像时图像中每像素对应的空间尺寸约为0.23 mm,而粘贴在待测平面的标志点内圆心直径为 5 mm.
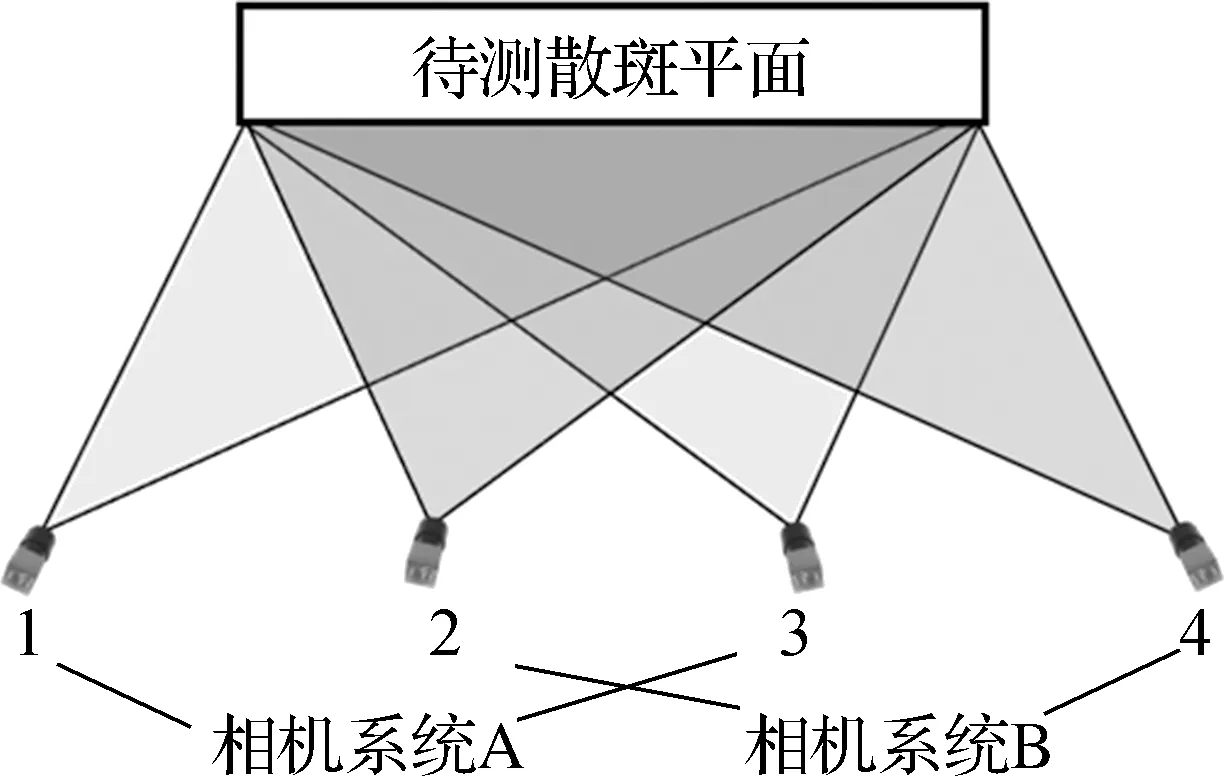
(a) 相机系统布置图

(b) 实验装置布置图
平移实验开始前,对静止的待测平面进行一段时间的噪声采集,用以评估2套DIC测量系统的整体误差水平.由于2套DIC测量系统对称布置,在此以相机系统A为例进行说明,计算区域取全部散斑区域,具体系统误差(静态噪声水平)结果如图5和表1所示.可以看到:该测量系统计算的面内位移u和v均值在±0.005像素内波动,离面位移w均值在±0.02像素内,表面应变εxx、εxy和εyy均值范围为±25×10-6.因此可以认为待测物体静止不动时,该测量系统的面内位移误差为0.01像素(约为0.002 3 mm).
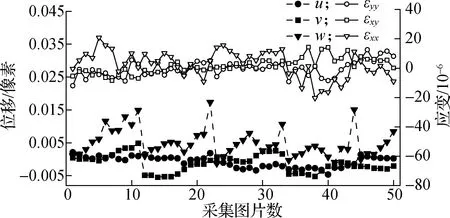
图5 相机系统A测量结果的均值

表1 相机系统A测量噪声

(a) 不同平移距离时un的统计误差
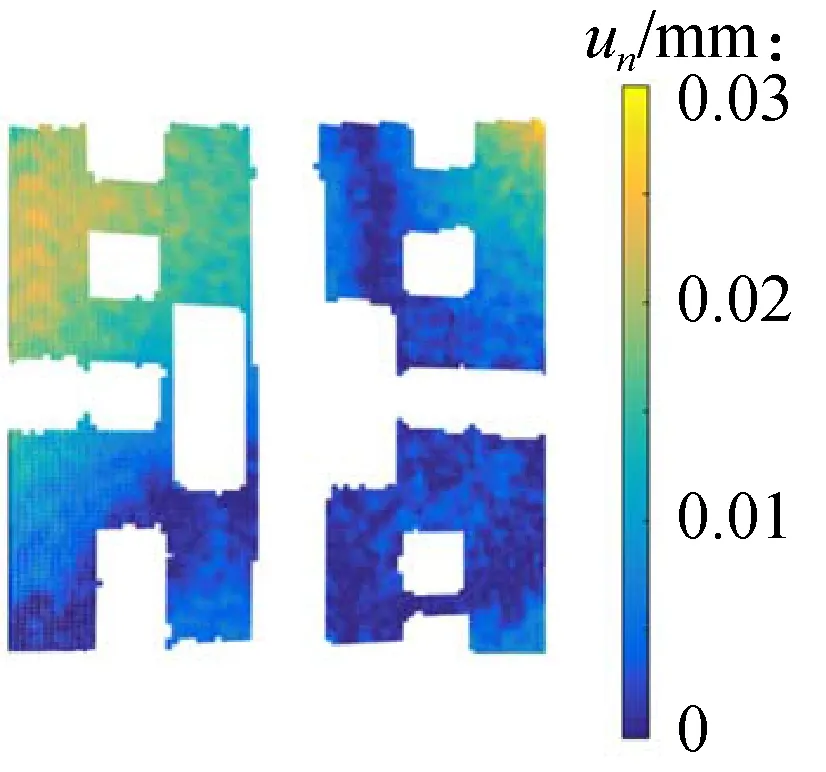
(b) 平移70 mm时un的分布云图
3 BFRP筋海水海砂珊瑚-UHPC组合梁的抗弯实验
为验证基于标志点多相机测量方法的有效性,本文以BFRP筋海水海砂珊瑚-UHPC组合梁[29]为研究对象,测量混凝土梁在加载过程的全场位移和全场应变情况,并与位移计结果进行对比分析.
3.1 试样准备
混凝土梁试件尺寸均为2 400 mm(长)×120 mm(宽)×240 mm(高),在净跨l0为2.1 m和剪切跨度为0.75 m的条件下进行四点弯加载实验,具体实验加载情况如图7(a)所示.其中采用的钢筋均为HPB235级,混凝土梁底部受拉筋为2根直径13 mm的BFRP筋,顶部使用2根直径10 mm的BFRP筋和30 mm厚的UHPC替换层,而所有箍筋均为8 mm的BFRP筋,图7(b)中给出了混凝土梁截面的示意图.
在梁底部和两支座处共布置了9个线性差动变压器式位移计(linear variable differential transformer,LVDT)用于测量梁的竖向位移,其中7个位移计居中布置在梁下端处(测点①~测点⑦),位移计A、B布置在支座处上侧,用以抵消末端位移,如图7(b)所示.此外,在顶部的受压区和底部的受拉BFRP筋处布有电阻应变片.
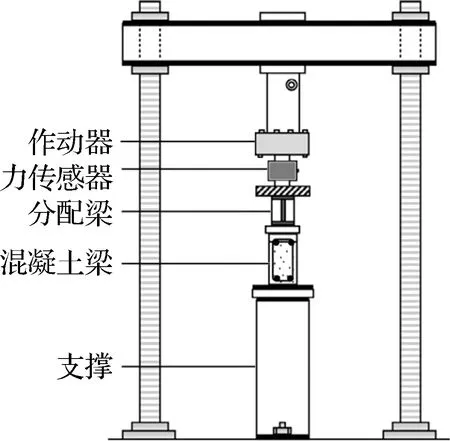
(a) 实验加载装置示意图
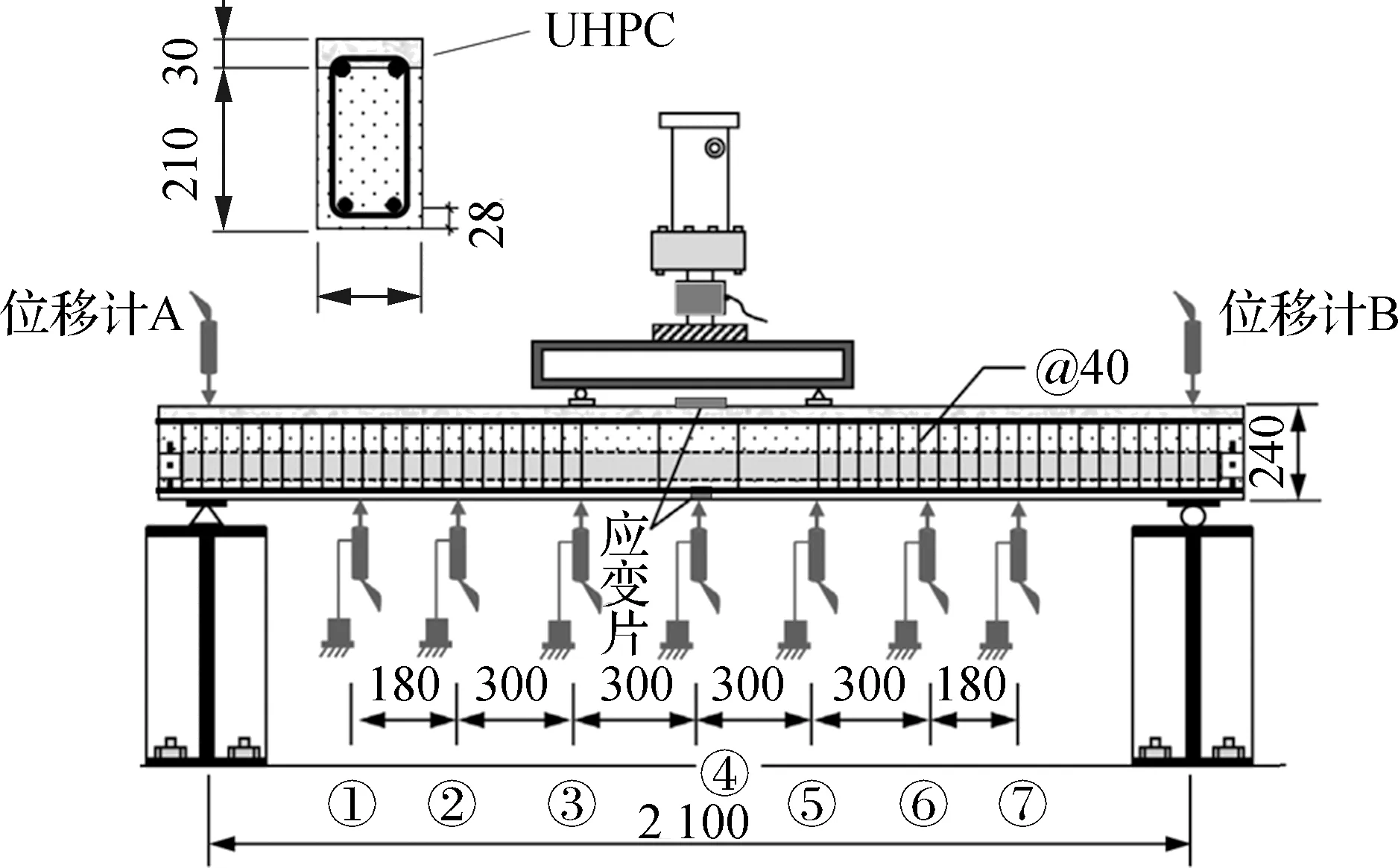
(b) 测量传感器布置图(单位:mm)
3.2 实验方案
利用6台工业相机、一台单反相机和图片采集设备搭设多相机三维DIC测量系统(见图8)进行混凝土梁的测量实验,其中每2台相机为一套三维DIC子系统,相机的视场和布置方式见图9.由于实验场地的限制(加载装置的立柱和周围设备的围挡),相机的数量和可工作距离受到限制,因此选取了视场较大的8 mm焦距镜头和85 cm测量距离进行图像采集,而畸变和视角过大则导致实际可计算的测量区域约为900 mm×900 mm.其中,各工业相机均为2 048×2 048像素,用于重构标志点坐标的便携式单反相机型号为Nikon D7100,选择颗粒直径为3 mm的水转印散斑到梁表面作为变形信息载体,使用单色照明光源均匀照明.

图8 实验现场测量设备布置图

图9 多相机测量系统布置图
搭设好测量相关设备后,利用标志点和标定板对相机的内、外参进行标定,最后各相机随加载设备启动同步采集图片.图10为加载实验开始之前标志点和碳纤维刚性标尺的布置方式,使用单反相机以不同姿态拍摄一系列图片,而各相机同时采集一次,由此完成有关标志点的标定步骤.其中,使用的标定板为棋盘标定板,以普通三维DIC的标定方式依次标定3套三维DIC子系统,而实验使用的编码标志点内圆心直径均为15 mm,正方形轮廓边长为43 mm.

图10 标志点和碳纤维刚性标尺
进行数据处理时,计算选取的子集大小为19×19 像素(3套DIC子系统从左到右分别对应为97×296、91×298和93×301个计算点),网格步长设为9 像素.
3.3 实验结果
图11给出了BFRP筋海水海砂珊瑚-UHPC组合梁在荷载为137.613 kN(破坏临界载荷)时,由多相机三维DIC系统测得的全场位移图和全场应变图.由图11(b)可以观察到,全梁从左侧支座开始位移v(即梁挠度)由逐渐增大到分配梁处趋于平缓,最后再逐渐减小,符合理论梁在四点弯曲加载时竖向位移的分布趋势.图11(c)~(e)为全场应变云图,其中图11(c)中由开裂产生的虚应变εxx最大值主要集中在梁中部下侧,随下侧混凝土受拉开裂向上开展;而在图11(d)中由剪切破坏造成的斜裂缝对应的应变εxy分布在梁两侧,数值相反.相较传统双相机三维DIC方法,实验共使用了6台相机组成多相机测量系统,变形测量分辨率对应提高3倍,因此通过加载-变形-破坏全过程的应变云图可以更好地对裂缝的形成与扩展进行分析.

(a) 全场x方向位移u

(b) 全场y方向位移v

(c) 全场应变εxx

(d) 全场应变εxy

(e) 全场应变εyy
图12为在实验过程中混凝土梁下端各测点的挠度随荷载加载变化的测量结果,该测量结果分别由LVDT位移传感器和DIC方法获得.如图所示,测点①处由2种方法测得的挠度曲线在整个加载过程中走势一致,结果基本重合;测点②和测点③处由2种方法测得的挠度曲线在荷载不大时基本吻合,而随着加载荷载的增大,DIC方法的测量结果稍大于位移传感器结果,且测点③相较于测点②更为明显,这是因为位移传感器的测点随着梁挠度的增大发生了水平滑移,导致其测量结果偏小;测点④处由2种方法测得的挠度趋势和结果基本一致,而DIC结果仍稍大于位移计结果,这可能是位移传感器在安装时与竖直方向有一定夹角而导致的.考虑实际工程使用的情况下,在使用多相机三维DIC测量方法来计算混凝土梁的挠度时,其结果的一致性和稳定性会更好.
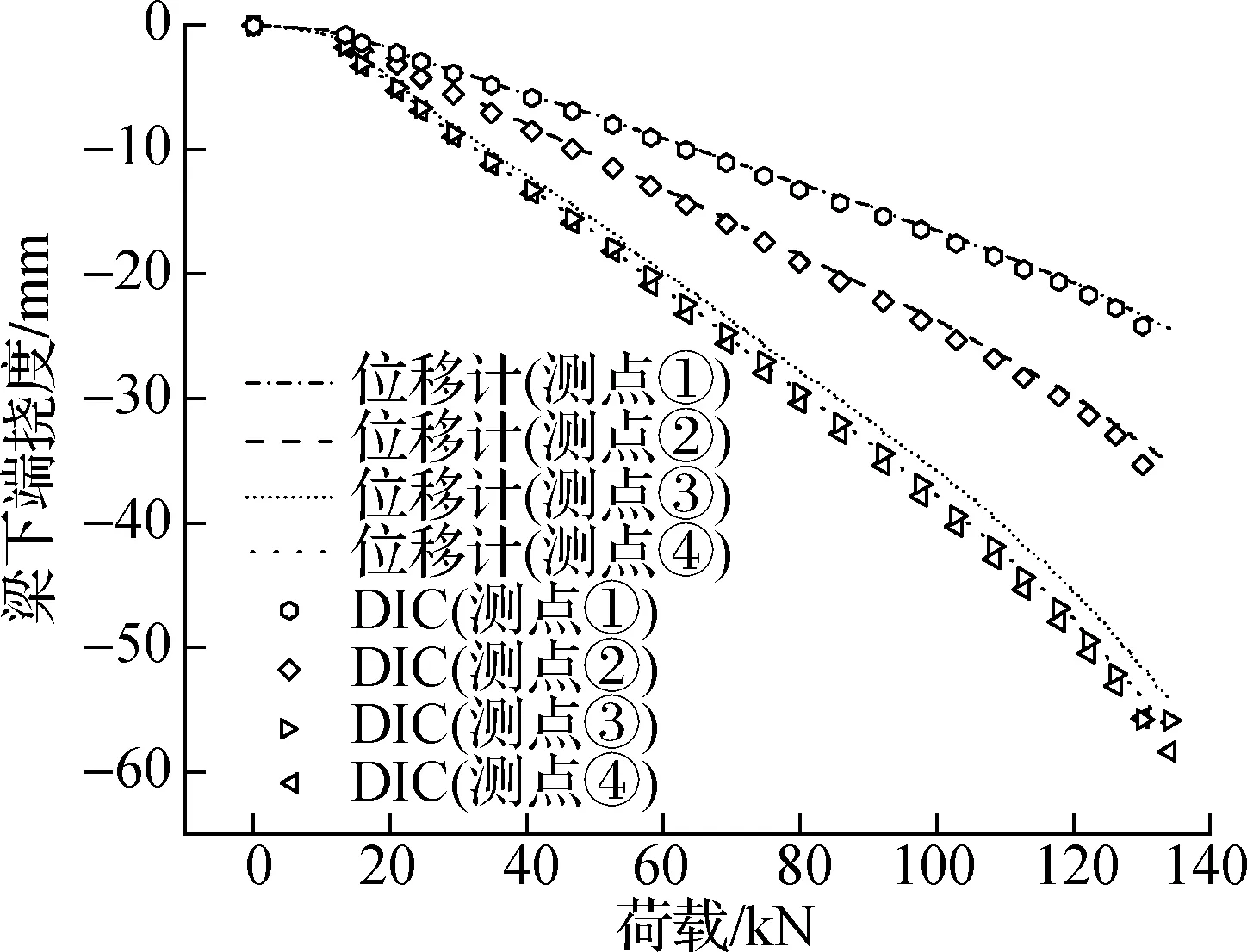
图12 由DIC和位移传感器测得梁下端挠度图(竖直向上为正)
4 结论
1) 实验室电动平移台实验表明,拼接误差un的均值与位移距离呈线性关系,但相对误差始终小于0.03%且σu小于0.01 mm,说明基于标志点的多相机测量方法得到的坐标系统一精度满足工程需求.
2) 将该方法用于混凝土梁的加载实验,获得了极限荷载下的全场位移和全场应变结果,且位移测量结果与位移计结果基本一致.
3) 相对于传统双相机三维DIC方法,该方法变形测量分辨率提高3倍;相对于使用重叠视场的多相机DIC方法,其测量结果不会引起误差传递,同时可减少一半标定时间,因此基于标志点的多相机方法具有操作简便、布置灵活且应用场景广泛的特点.
4) 针对该方法在大尺度、复杂工程环境下的应用,有以下几点需要继续完善:标志点的识别精度和重构精度需要进一步提高;当土木工程构件尺寸过大时,需要解决标志点难以粘贴布置的问题;简化多相机测量系统的现场布置方式.
