波形钢腹板箱梁考虑腹板局部纵向刚度影响的扭转效应分析
2021-04-20张元海孙成成
张元海 孙成成
(兰州交通大学土木工程学院, 兰州 730070)
波形钢腹板组合箱梁是一种较为新颖的轻型化桥梁结构,近年来得到了迅速的推广和发展.但以波形钢板作为箱梁腹板时,箱梁截面的抗扭刚度会显著下降,由截面扭转产生的纵向翘曲正应力与弯曲正应力的比例超过了传统混凝土箱梁[1].这表明,波形钢腹板组合箱梁的扭转效应是实际工程中应考虑的关键因素.随着国内外学者对该桥型结构的深入研究[2-5],其理论计算方法也日益成熟.李宏江[6]基于薄壁梁扭转的乌曼斯基第二理论推导了波形钢腹板箱梁的约束扭转微分方程及翘曲正应力和剪应力计算公式,并且考虑到波形钢腹板的手风琴效应,将波形钢腹板的纵向刚度予以忽略,即腹板全截面正应力为零.Qiao等[7]将波形钢腹板箱梁截面全部换算为钢截面,计算了波形钢腹板箱梁的翘曲正应力及剪应力,同时通过波形钢腹板的表观弹性模量将其纵向刚度予以忽略.文献[8-11]也进行了类似理论推导和试验研究,均将波形钢腹板全部截面刚度予以忽略.现行规范[12]规定波形钢腹板箱梁受轴向力时,可完全忽略波形钢腹板的纵向刚度,但并未对受弯或受扭情况时的腹板纵向刚度做明确规定.作者认为,就单独的波形钢腹板而言,其纵向刚度确实很小,可忽略,但对组合箱梁的波形钢腹板,其上下端部区域必然受到顶底板的牵制,分析中应考虑这种情况.
本文在薄壁箱梁经典理论的基础上,考虑了波形钢腹板的几何特性以及混凝土顶底板对波形钢腹板的约束作用,使理论计算结果更加符合波形钢腹板箱梁的实际受力情况.同时分析了波形钢腹板组合箱梁的扭转应力,并提出一种扭转正应力在波形钢腹板上的分布模式,结合数值算例对比分析了与传统方法计算结果及有限元结果的差别.最后分析了悬臂板相对宽度和腹板厚度变化对约束扭转效应的影响.
1 波形钢腹板的力学性能分析
1.1 波形钢腹板的共同抗弯区
图1为左右对称的波形钢腹板箱梁横断面简图.其中a、b、c分别为底板、顶板、悬臂板宽度,tu、tb分别为顶板、底板厚度,h为梁高,h1为波形钢腹板高度.
考虑箱梁顶底板对波形钢腹板的约束作用,根据文献[6]中试验数据及本文有限元分析结果,对波形钢腹板上与顶底板相接区域范围,考虑其局部纵向刚度,即该区域与顶底板共同抵抗梁体弯曲应力,称该区域为波形钢腹板的共同抗弯区.如图1所示,h′表示波形钢腹板上翘曲应力分布高度,令h′=δh1,其中δ为腹板共同抗弯区高度与腹板高度之比.对波形钢腹板上共同抗弯区以外区域,则考虑手风琴效应, 忽略其局部纵向刚度.

图1 波形钢腹板组合箱梁横断面
1.2 波形钢腹板的弹性模量
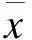
(1)
(2)
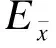
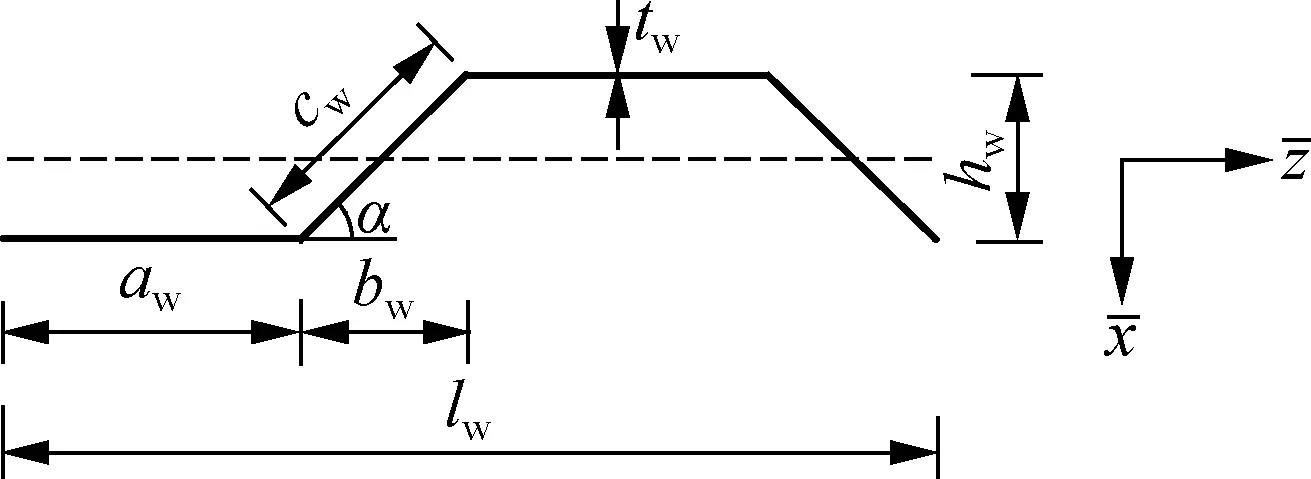
图2 波形钢腹板简图
1.3 波形钢腹板的剪切模量与等效截面
等效为正交异性板后,波形钢板的有效剪切模量Ge通常小于钢板材料的剪切模量Gs[14],其计算公式为
(3)
式中,Gs=Es/[2(1+v)],v为钢板泊松比.
考虑到波形钢腹板箱梁扭转时以抗剪为主[15],因此通过剪切模量比将波形钢腹板换算为混凝土板进行计算.换算后混凝土板厚度tcw为
(4)
式中,Gc为混凝土的剪切模量.
2 约束扭转翘曲正应力
根据乌曼斯基第二理论及其基本假设[16],约束扭转时箱梁的纵向位移为
(5)

根据箱梁截面的周边不变形假定得到波形钢腹板箱梁的扭转翘曲正应力,即
(6)
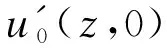
然后由自平衡条件,整理可得
(7)
根据约束扭转双力矩的定义可得

(8)



(a) 传统广义扇性坐标示意图
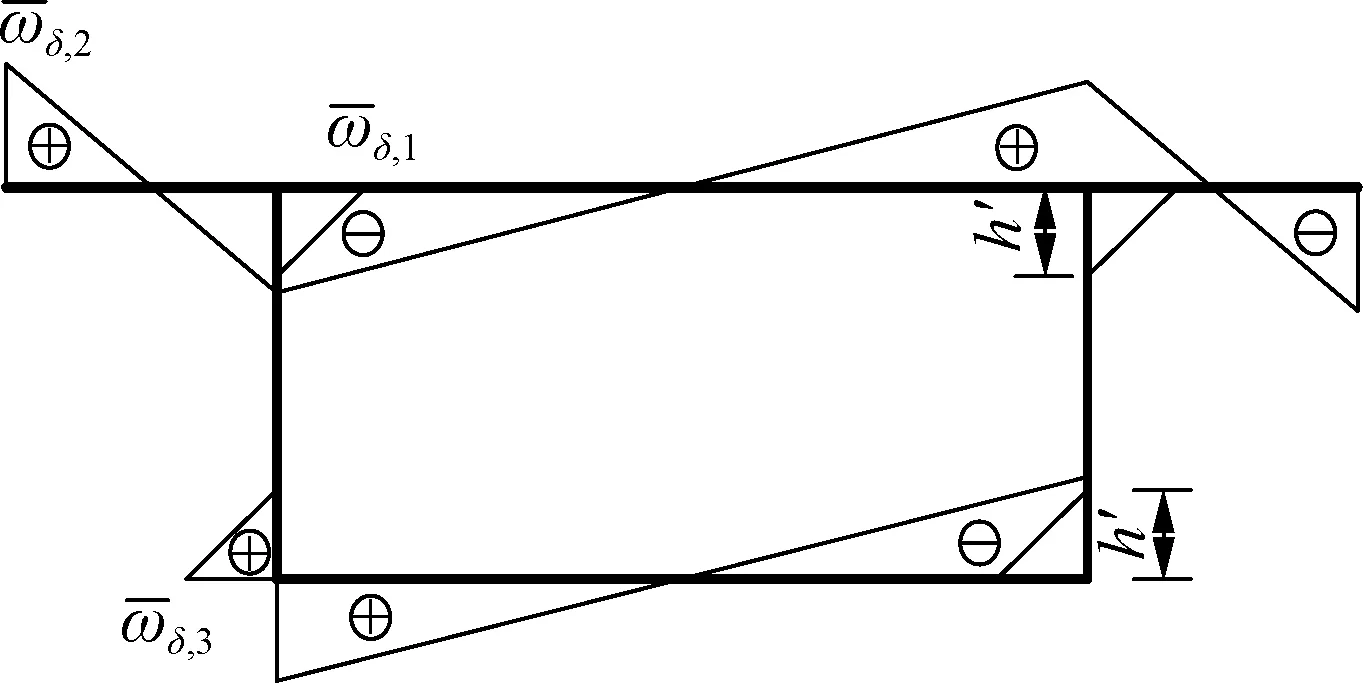
(b) 波形钢腹板箱梁广义扇性坐标示意图
得到波形钢腹板箱梁的广义主扇性惯性矩为
(9)

(10)
将式(10)代入式(7)得到波形钢腹板箱梁的翘曲正应力计算公式,即
(11)
综上可知,求解正应力σω必须先求得广义翘曲位移β′.根据乌曼斯基的薄壁梁约束扭转分析理论,可建立微分方程如下[17]:
(12)


(13)

广义翘曲位移β′与扭转角φ的关系为
Mz=GcIρ(φ′-μβ′)
(14)
式中,Mz为梁体总扭矩;Iρ为极惯性矩.
通过初参数法[17-18],并结合边界条件对微分方程进行求解.根据式(14)得到广义翘曲位移,最终代入式(10)、(11)即可求得波形钢腹板箱梁的翘曲正应力.
3 数值算例分析
3.1 算例简介
算例采用图4所示的简支梁,截面几何参数如图4(a)所示,梁端为矩形横隔板.波形钢腹板使用900型,形状尺寸如图4(b)所示.在跨中截面左腹板上方施加竖向偏心荷载P=1 MN,偏心距e=2.7 m.混凝土弹性模量Ec=34.5 GPa,泊松比vc=0.2;钢材弹性模量Es=206 GPa,泊松比vs=0.3.

(a) 组合箱梁尺寸

(b) 波形钢腹板尺寸
为了进行对比分析,建立ANSYS有限元模型,如图5所示.使用SOLID45实体单元模拟混凝土板和横隔板,使用SHELL63壳单元模拟波形钢腹板.简支梁端约束底排节点,其中一端约束Ux、Uy、Uz三个方向的位移,另一端约束Ux、Uy两个方向的位移.

图5 ANSYS有限元模型
根据偏心荷载分解法分离出扭转荷载,如图6所示.使用MPC184单元在截面扭转中心O处建立一个节点,与顶底板和腹板上的节点分别形成多根刚性梁,从而形成刚性面.最后将转化后的扭矩加载到中心节点O上,达到施加扭转荷载的目的.

图6 分解的扭转荷载
3.2 约束扭转翘曲正应力计算


表1 不同δ值时的扭转参数值
通过式(11)计算出不同δ值时A1、A2、A3三个计算点的翘曲正应力,同时与文献[8]中完全忽略腹板抗弯性能的传统求解方法及有限元求解得到的翘曲正应力结果进行对比,列于表2.

表2 翘曲正应力对比 kPa
由表2可看出,波形钢腹板共同抗弯区高度对箱梁截面的翘曲正应力有较大影响.传统方法计算结果相比本文方法计算结果偏小约3%,相比有限元计算结果偏小约7%,本文计算结果较传统方法结果与有限元结果更为接近.
最终结合文献[6]中试验数据及本文有限元分析中翘曲正应力在腹板上的分布情况确定出共同抗弯区高度h′,取δ=0.10,即h′=0.10h.绘制的跨中截面翘曲正应力如图8所示.
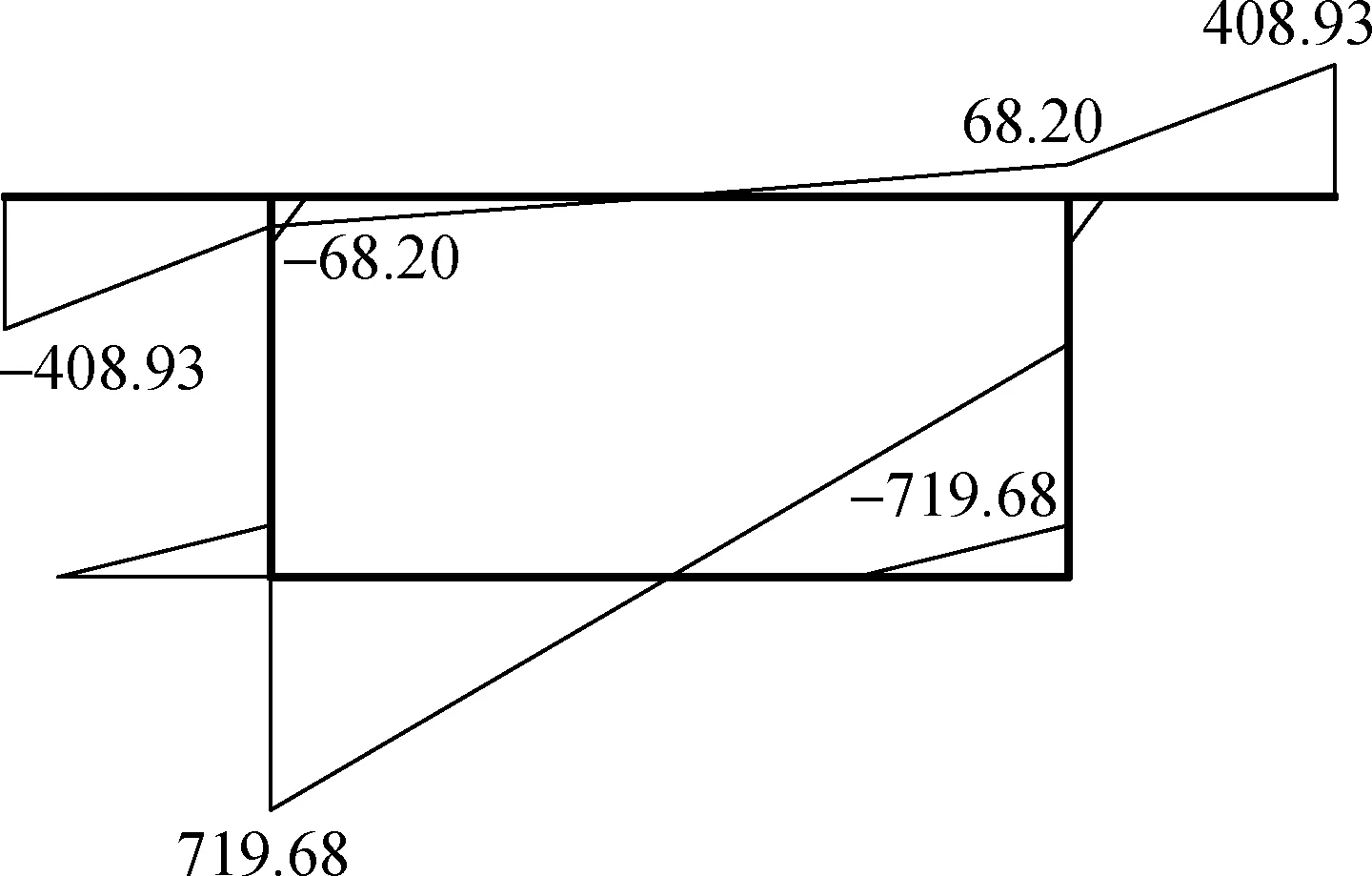
图8 跨中断面翘曲正应力(单位:kPa)
表3分别列出了应用本文方法和传统方法所得到的跨中断面处扭转角φ(z)与广义翘曲位移β′(z)的计算结果.分析可知,考虑腹板局部抗弯性能后的计算结果稍大于传统方法计算结果,但两者基本接近.可知,波形钢腹板箱梁的腹板纵向刚度对扭转角和广义翘曲位移的影响很小.

表3 跨中断面扭转角与广义翘曲位移
表4分别列出了应用本文方法、传统方法与有限元求解得到的跨中断面A2、A3两点处(见图4(a))的纵向位移u2、u3和横向位移v2、v3的计算结果.分析可知,考虑腹板局部抗弯性能后的计算结果稍大于传统方法计算结果,但两者基本接近,因此可知,波形钢腹板箱梁的腹板纵向刚度对梁体纵横向位移的影响不大.解析解与有限元数值结果相比也基本一致,误差可能由应力集中现象以及解析法的刚周边等基本假设造成.

表4 跨中断面纵向位移与横向位移
3.3 参数分析
为了研究箱梁几何参数变化对翘曲正应力的影响,引入正应力系数η,其定义为翘曲正应力与弯曲正应力之比的绝对值.使悬臂板宽度从0开始以0.3 m为步长逐渐增大至5.4 m,顶板宽度不变,正应力系数η随悬臂板宽度比(c/b)的变化曲线如图9所示.

图9 正应力系数随悬臂板宽度比变化曲线
由图9可看出:悬臂板相对宽度的变化对悬臂板和顶底板的翘曲正应力均有较大影响;随着悬臂板相对宽度的增大,悬臂板和底板端点的正应力系数呈现先增大后减小的规律,悬臂板宽度比在0.45左右时,正应力系数达到最大值0.35,这说明约束扭转翘曲正应力可达到弯曲正应力的35%左右;A2点的正应力系数呈现先减小后增大的规律,当悬臂板宽度比在0.45左右时接近于零,这说明此时A2点翘曲正应力的方向发生了改变.在实际工程中,悬臂板宽度比一般在0.5左右,因此A1、A2、A3三个计算点的正应力系数可分别取0.28、0.02和0.34.
图10为正应力系数随腹板厚度tw的变化曲线,参照已建成的波形钢腹板箱梁桥,使波形钢腹板厚度从6 mm开始以2 mm为步长逐渐增至20 mm.分析表明:波形钢腹板厚度的变化对正应力系数影响显著;随着腹板厚度的增大,悬臂板和底板端点的正应力系数单调减小,当tw=6 mm时,正应力系数可达到0.45,这说明约束扭转翘曲正应力可达到弯曲正应力的45%;A2点的正应力系数呈现先减小后增大的规律,当波腹板厚度在12 mm左右时接近于零,这说明此时A2点翘曲正应力的方向发生了改变.
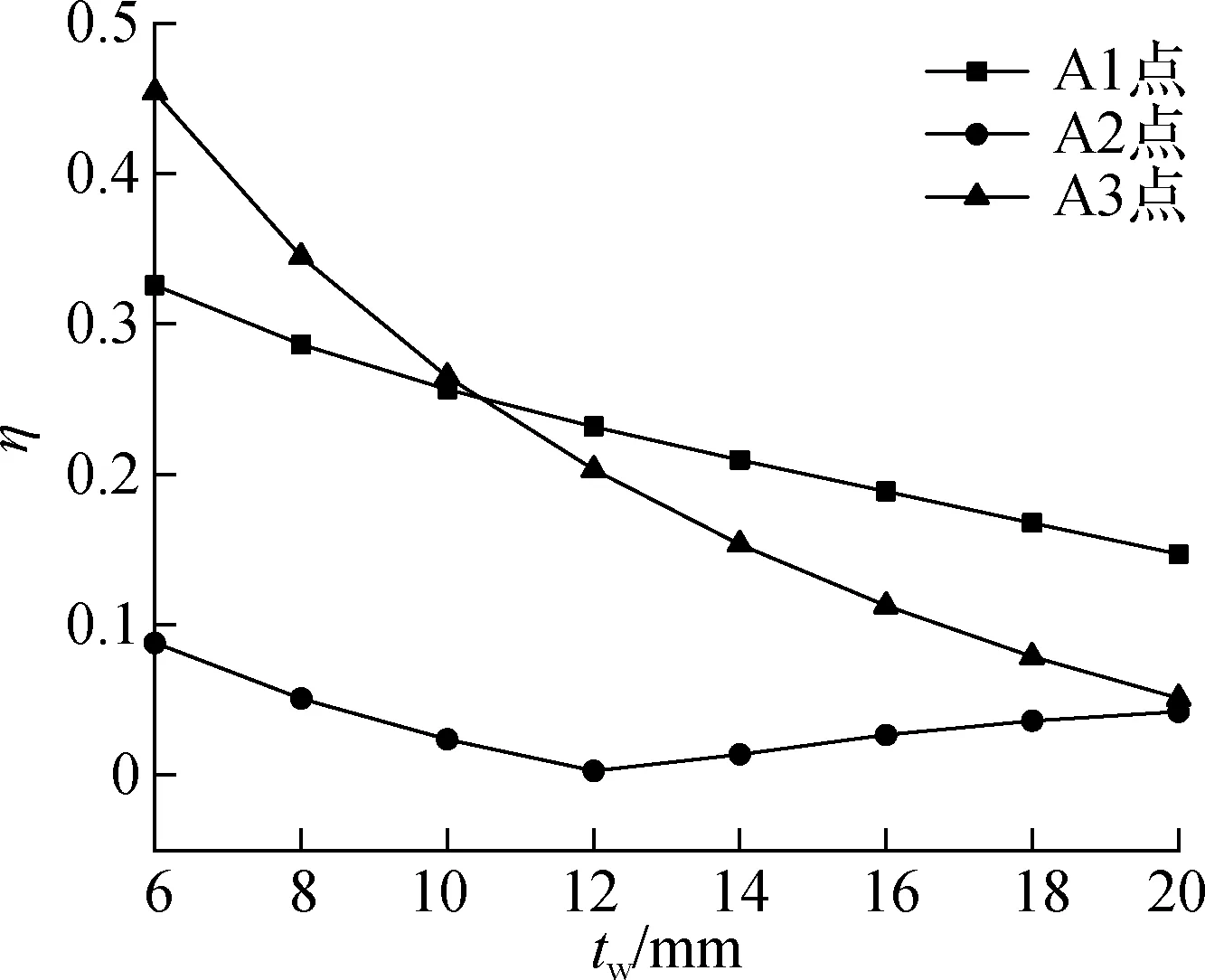
图10 正应力系数随腹板厚度变化曲线
4 结论
1) 本文提出了一种约束扭转翘曲应力的求解方法,考虑了顶底板对波形钢腹板的约束作用,通过等效截面的途径,推导了波形钢腹板组合箱梁的约束扭转翘曲正应力计算公式,数值算例及有限元分析验证了本文方法的正确性.
2) 针对波形钢腹板箱梁提出了一种新的广义扇性坐标分布模式,计算了约束扭转翘曲正应力,其计算结果相比传统计算方法精度更高.
3) 取腹板高度的10%作为波形钢腹板共同抗弯区高度,相比完全忽略腹板抗弯性能的传统计算方法具有更好的计算精度.
4) 考虑顶底板对腹板的约束效应可使理论计算结果更加符合波形钢腹板箱梁实际受力情况,且波形钢腹板共同抗弯区内的翘曲正应力可达到弯曲正应力水平,因此不宜忽略.
