铰接钢框架-自复位耗能支撑子结构抗震性能试验研究
2021-04-20舒赣平
舒赣平 李 然
(1东南大学土木工程学院, 南京 211189)(2石家庄铁道大学土木工程学院, 石家庄 050043)
形状记忆合金(SMA)具有超弹性性能,最大可恢复变形可达7%以上,是理想的耗能和复位材料.国内外很多学者致力于将SMA作为复位材料应用于自复位耗能装置[1-9].研究中采用的材料形式包括SMA丝、SMA棒和SMA螺旋弹簧等.单一的SMA或是包含SMA的复合材料都可作为耗能和自复位部件.目前的研究大多针对结构或装置的最大位移、层间位移角、残余变形、滞回性能等,且发现基于SMA的自复位耗能装置的耗能性能一般或复位能力不足.此外,关于自复位耗能装置的研究多止于构件层面,仅少数进行了体系层面的数值模拟研究,且缺乏相关试验研究.
本文利用形状记忆合金的超弹性性能,设计了一种兼具耗能和自复位性能的自复位耗能装置,将其与支撑串联后安装在铰接钢框架-支撑结构中,形成铰接钢框架-自复位耗能支撑子结构.对该子结构的抗震性能进行试验研究,以验证装置在结构体系中的适用性.
1 SMA自复位耗能装置
图1为SMA自复位耗能装置(SMA-SCED)的构造示意图.图中,LD为SMA丝束的设计长度;δ为SMA丝束的设计最大变形量.该装置主要由外筒、端板、中间板、拉压杆和SMA丝束等组成,其核心部件为SMA丝束.装置外筒各段通过螺纹连接,左拉压杆一段和左拉压杆二段通过螺纹相连,中间板1和中间板2放置于外筒内部并分别与外筒二段左侧、外筒四段右侧顶紧,右拉压杆与右端板、左右端板与外筒之间均采用螺纹连接,SMA丝束通过中间板1和中间板2上的开孔缠绕在两中间板之间,并用U形卡锚固.通过改变外筒各段之间及左拉压杆两段间的螺纹旋合长度,来调节SMA丝束预应力的大小.
图2给出了装置的工作原理示意图.如图2(a)所示,假设装置右端固定不动,装置轴向受拉时,左拉压杆拉动中间板1向左运动,中间板2受到外筒的限制保持不动,SMA丝束由于两中间板相对距离的增大被拉长.当中间板1向左运动至左端板右侧时,SMA丝束伸长量达到设计最大变形量δ.此时,若外荷载继续增大,外荷载由SMA丝束及外筒共同承担,直至装置破坏;若外荷载减小,由于受到SMA丝束回复力的作用,中间板1向右运动直至回复到初始位置.装置轴向受压(见图2(b))时的工作原理与轴向受拉时工作原理相同.
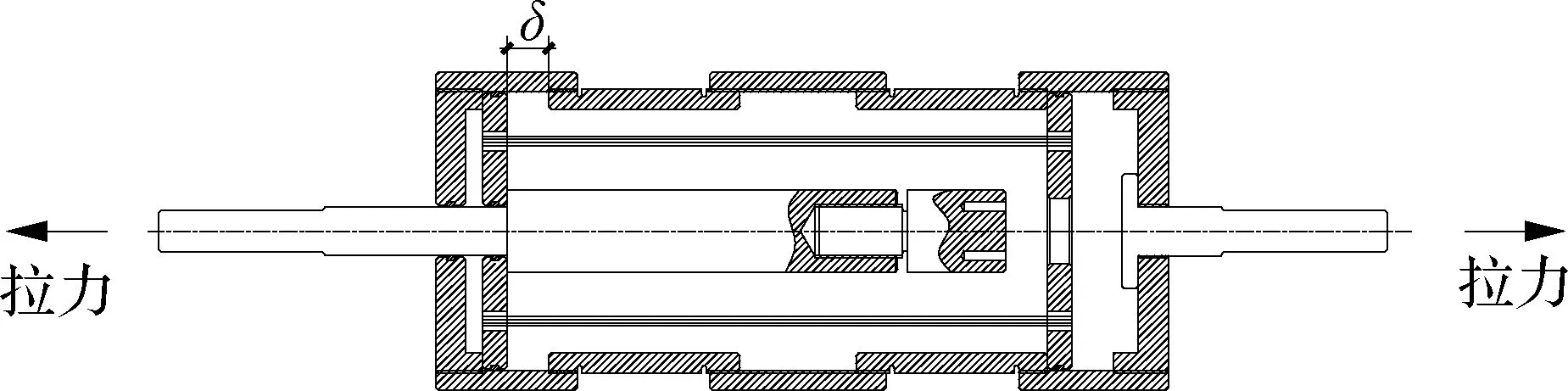
(a) 拉伸

(b) 压缩
装置在轴向拉、压作用下均通过中间板1和中间板2相对距离的变化来实现SMA丝束的拉伸与回缩.在此过程中,无论外荷载形式为拉还是压,SMA丝束始终处于受拉状态(即耗能状态),因而在整个受荷载过程中可发挥耗能和复位功能.
2 模型设计
2.1 概念模型
根据试验室设备和场地条件,设计制作了一榀1∶2缩尺的两层单跨平面铰接钢框架-自复位耗能支撑子结构SF-CEB.设计时考虑SMA-SCED的轴向受力特性,将其与子结构支撑部分串联形成自复位耗能支撑.子结构基本模型见图3,跨度L=3 m,层高H=1.5 m.
2.2 设计准则
1) 以SF-CEB子结构屈服时达到结构层间位移角限值为原则,确定自复位耗能支撑各项参数.
2) SF-CEB子结构达到弹性层间位移角限值时自复位耗能支撑屈服,卸载后无残余变形,结构性能不受影响.
3) SF-CEB子结构变形超出弹性位移角限值但未超出弹塑性位移角限值时,自复位耗能装置发挥耗能作用,消耗地震能量,卸载后子结构残余变形减小甚至消失,达到自复位的目的.
2.3 构件设计
2.3.1 梁、柱截面设计
由于SF-CEB子结构采用铰接连接,故其梁、柱无弯矩作用.经初步设计,该子结构的梁、柱均采用焊接H形钢,截面尺寸h×b×tw×tf分别为200 mm×125 mm×8 mm×10 mm和150 mm×150 mm×8 mm×10 mm,其中,h为构件高度,b为构件宽度,tw为腹板厚度,tf为翼缘厚度.支撑段采用轧制圆钢管,外径d=114 mm,壁厚t=8 mm.每个柱顶施加410.4 kN的集中荷载,以模拟结构的上部荷载.令F为施加于柱顶的轴压力,f为材料的抗压强度设计值,A为柱的截面积,则轴压比计算公式为
由此可求得施加于钢柱的轴压比n=0.334.
2.3.2 自复位耗能支撑设计
由图3可见,自复位耗能支撑由一段普通支撑与一个SMA-SCED组成.将2个自复位耗能支撑组成的体系称作自复位耗能支撑体系,2根柱和1根梁组成主框架,主框架和自复位耗能体系构成一个基本结构单元.基本结构单元在水平荷载作用下发生变形,变形前、后分别如图4中实线和虚线所示.令SMA-SCED的弹性模量、面积和初始长度分别为ED、AD、lD;普通支撑段的弹性模量、面积和初始长度分别为EB、AB、lB;自复位耗能支撑的总长度为l;在水平荷载F0作用下,基本结构单元产生的水平和竖向位移分别为δ0和δH.则水平荷载作用下SMA-SCED装置的长度变化为
(1)
水平荷载F0与水平位移δ0的关系可表示为
(2)
(3)

图4 基本结构单元关系
经设计,取自复位耗能装置核心SMA丝束长度lSMA=300 mm,面积ASMA=760 mm2,装置其他构件根据构造措施进行设计.
2.4 材料性能
SF-CEB子结构中装置核心部分采用Ni-Ti SMA丝.试验测得SMA丝的各性能指标为:奥氏体弹性模量EA=54.4 GPa,马氏体弹性模量EM=40.8 GPa,马氏体相变开始应力σMs=388 MPa,马氏体相变完成应力σMf=623 MPa,奥氏体相变开始应力σAs=166 MPa,奥氏体相变完成应力σAf=80 MPa,最大相变应变εL=5.3%.
设计时保证装置中其他部件在荷载作用下始终处于弹性受力阶段.除SMA外,装置其他部件的材料性能见表1.SF-CEB子结构梁、柱均采用焊接H形钢,支撑采用热轧无缝钢管.

表1 SF-CEB子结构各部件材料性能
3 试验
3.1 试验装置
SF-CEB子结构总体装配图如图5所示.子结构东西向布置,反力墙位于西侧,子结构位于反力墙东侧.一、二层分别采用50 t 201.45型和150 t 201.70型液压伺服作动器施加水平荷载,并采用柱内预应力的方式模拟上部结构荷载.为防止SF-CEB子结构发生面外失稳,采用4个柱侧向支撑和2个梁侧向支撑对其面外位移进行约束.

图5 试验总体装配图
3.2 加载制度
试验时,施加在结构二层和一层的水平荷载比值为20∶1.根据底部剪力法基本理论,该荷载模式可以模拟六层结构的倒三角分布模式.加载时采用双作动器联动加载的位移-力混合控制制度[10],即二层作动器为主动控制作动器,采用位移控制;一层作动器为被动控制作动器,采用力控制.结构荷载-位移曲线出现明显拐点时视为结构屈服,结构承载力降低至峰值荷载75%时认为结构破坏,停止加载.上下层框架同步、分级加载,二层作动器的加载历程如图6所示,幅值0~40 mm为弹性加载阶段,幅值40~90 mm为耗能阶段.

图6 加载制度
3.3 测量系统
为了获取结构位移及应变的变化情况,利用位移传感器、应变片及数字图像处理(DIP)技术对结构梁、柱、支撑等的位移、应变、变形等进行测量与监测.SF-CEB子结构测点分布情况见表2.

表2 SF-CEB子结构测点分布情况
4 试验现象与结果
正式加载前,先对结构二层进行2次幅值为5 mm的预加载循环,以检查操作控制系统及数据采集系统的运行情况.为便于描述,规定加载方向以推为正,以拉为负.整个加载过程中SF-CEB子结构未发生破坏,结构的荷载-位移曲线见图7.

(a) SF-CEB一层

(b) SF-CEB二层
4.1 试验现象
由于SF-CEB子结构中SMA-SCED的刚度远小于支撑段刚度,加载过程中自复位耗能支撑变形主要发生在装置段.SMA-SCED变形情况见图8.

(a) 东侧SMA-SCED拉伸前

(c) 西侧SMA-SCED拉伸前
加载第1阶段,结构的承载力随加载幅值的增大呈线性增长.当加载幅值超过40 mm时,结构刚度开始变小,加载进入第2阶段,加载过程中结构的承载力缓慢增长,且未发现结构破坏.受柱侧向支撑顶杆长度所限,负向加载至幅值80 mm时柱翼缘已基本与侧向支撑顶杆端部接触.为确保试验设备的安全,仅对正向90 mm幅值进行了1次循环加载,框架最大承载力达到701.4 kN.
4.2 试验结果
4.2.1 SF-CEB子结构位移
图9为SF-CEB子结构柱在不同加载幅值下水平位移与层剪力的关系曲线.由图可见,随着加载幅值的增大,结构位移-剪力曲线呈折线形增长.加载初期,结构刚度较小.随着加载幅值的增大,结构刚度呈线性增长.当一、二层加载幅值分别增至20和40 mm时,结构刚度发生改变,这是因为SF-CEB子结构中SMA-SCED的核心部件SMA丝束在该加载幅值时发生屈服.

(a) 正向加载(一层)
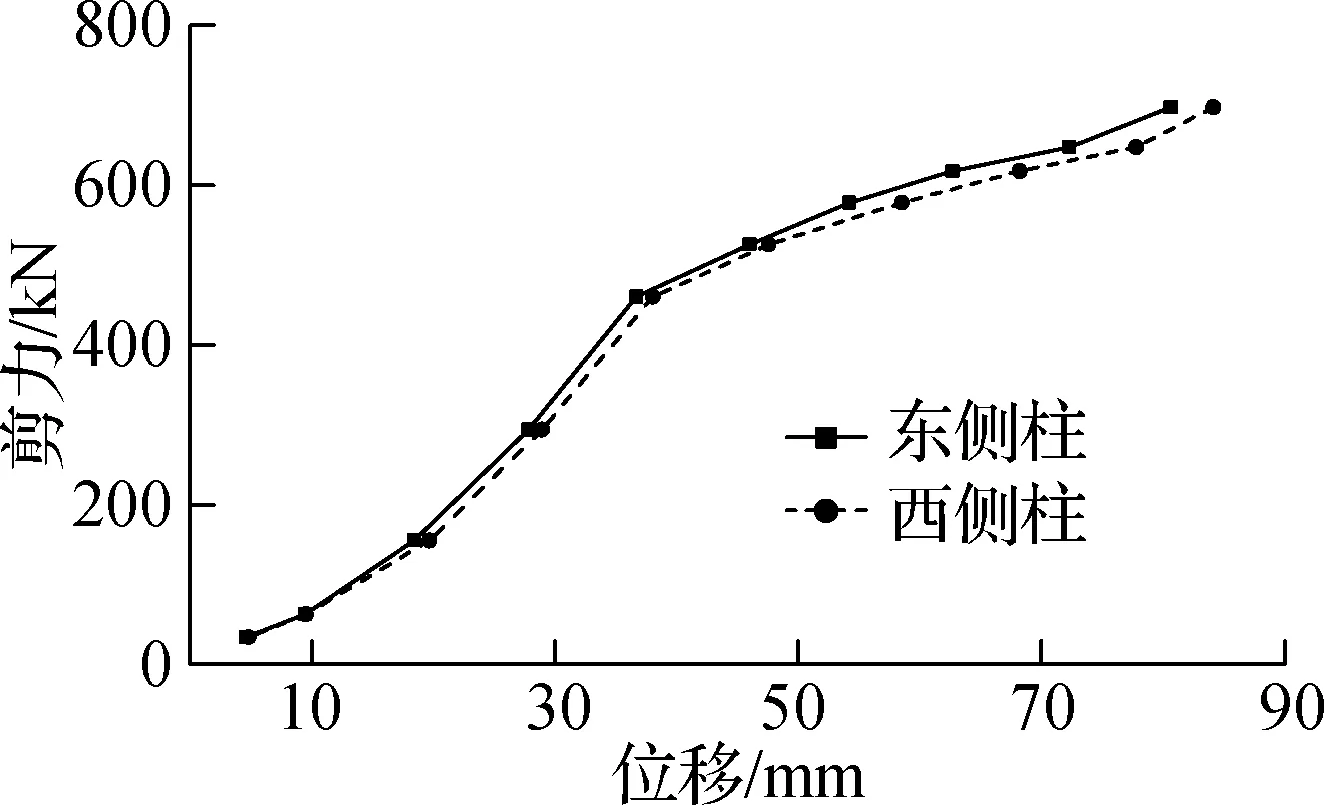
(c) 正向加载(二层)

(d) 负向加载(二层)
相同加载幅值正向加载时,结构西侧柱的水平位移较东侧柱略大,负向加载与正向加载具有相同的趋势,构件间的间隙是造成这种差别的主要原因.
图10给出了SF-CEB子结构梁跨中位置竖向位移随加载幅值的变化情况.由图可知,梁-支撑节点区受自复位耗能支撑交替拉压力的作用.正向加载时,一层梁先发生向下位移,加载幅值大于40 mm后,开始发生向上位移,且随着幅值的增大位移逐渐增大;二层梁始终发生向上弯曲,且位移随加载幅值的增大而增大,加载幅值为90 mm时,位移值约为3.96 mm;该过程中,二层梁变形始终大于一层梁变形.负向加载时,框架梁均呈现出向上弯曲的现象,该过程中二层梁的变形同样大于一层梁的变形.

(a) 正向加载

(b) 负向加载
分析自复位耗能支撑的变形情况发现,加载过程中自复位耗能支撑仅发生了轴向变形,且变形基本发生在SMA-SCED段.总体来看,支撑受压时的变形略大于相同幅值下受拉时的变形,差别保持在10%以内.
4.2.2 SF-CEB子结构应变
为研究SF-CEB子结构各构件内力情况,分别对其柱、梁及自复位耗能支撑的应变进行监测.测点S1~S56布置如图11所示.分别研究柱1/2层高、梁1/4跨和自复位耗能支撑中普通支撑段1/2跨各测点应变随加载幅值的变化情况.

图11 SF-CEB子结构应变片测点布置
由图12可见,子结构拉压作用下各柱应变基本呈对称分布,加载幅值不大于20 mm时的应变很小,这与加载初期子结构刚度偏小一致.受一层作动器加载点的影响,二层柱应变稍小于一层柱应变.加载过程中柱最大应变约574×10-6,始终处于弹性状态.

(a) 一层

(b) 二层
分析图13可知,加载过程中子结构梁的最大应变未超过1×10-3,同样处于弹性变形阶段.正、负向加载过程中,梁同一个测点的应力呈反对称分布.
由图14可知,子结构东、西两侧支撑段的应变呈反对称分布.正向加载时,东侧支撑受压,西侧支撑受拉;负向加载时,东侧支撑受拉,西侧支撑受压.

(a) 梁翼缘

(b) 梁腹板

(a) 一层支撑

(b) 二层支撑
随着加载幅值的增大,各支撑最大应变均未超过1.2×10-3,构件同样处于弹性受力状态.
综上可知,加载初期子结构刚度偏小,构件应变偏小;正、负向加载时,东、西两侧柱水平位移有所差别.究其原因在于,销轴连接造成的梁-柱、梁-支撑及柱-支撑等构件的连接之间存在间隙,水平荷载作用下,子结构构件变形需先克服构件之间的间隙.
5 结果分析
为了更好地分析SF-CEB子结构的各项性能,图15给出了SF-CEB子结构的水平剪力-层间位移骨架曲线.由图可见,该子结构刚度基本呈两阶段分布模式,弹性加载阶段刚度较大,耗能阶段刚度较小,且正负向加载时曲线呈反对称分布.

(a) 一层

(b) 二层
下面分别对子结构的各项性能进行分析,各性能参数取相应加载幅值下各循环的平均值.
5.1 屈服荷载及承载力
表3列出了SF-CEB子结构各层抗震性能的特征值.表中,Qmax、Δmax分别为子结构的最大剪力及其对应的层位移;Qy、Δy为子结构的屈服剪力及其对应的层位移;μ=Δu/Δy为子结构的延性系数,其中Δu为子结构极限位移;θmax为子结构的最大层间位移角.由于本试验中加载最大层间位移未达到子结构的极限位移Δu,计算延性系数时Δu用加载最大层间位移Δmax代替,即μ=Δmax/Δy,因此,实际子结构的延性系数大于计算值.由图15和表3可见,SF-CEB子结构一层压、拉方向的最大承载力分别为34.9和29.8 kN,二层压、拉方向的最大承载力分别为697.4和595.2 kN.SF-CEB子结构一层压、拉时的屈服承载力分别为26.1和24.8 kN,二层压、拉时的屈服承载力分别为515.3和511.4kN,均基本相等.框架达到屈服承载力后,刚度明显降低,但承载力仍继续增长,这与SMA-SCED核心SMA丝束的性能一致,整个加载过程尚未达到结构的最大承载力.

表3 SF-CEB子结构抗震性能特征值
5.2 延性
由表3可见,SF-CEB子结构一层正向和负向加载时的延性系数分别大于2.23和1.80,二层正向加载和负向加载时的延性系数分别大于2.26和2.06.正、负向加载时,子结构一层的层间位移角分别大于1/34.2和1/39.7 rad,二层分别大于1/32.1和1/36.5 rad.由于加载至最大幅值时,子结构承载力尚处于增长状态,未达到极限承载力,延性系数和层间位移角分别以最大加载幅值对应的位移值进行计算,因此,结构实际延性系数和层间位移角大于表3中的计算值.
5.3 耗能及复位性能
试验结果表明,SF-CEB子结构除SMA-SCED外,其余各部分在水平荷载作用下始终处于弹性状态.子结构中SMA-SCED核心SMA丝束的超弹性性能使其能够消耗部分能量,且卸载后装置变形可自行回复.表4给出了SF-CEB子结构在各加载幅值下的耗能及自复位情况.表中,ΔW为子结构的单圈耗能,即一次加卸载循环形成的荷载-位移曲线包围的面积,表征其耗能能力;η=ΔW/W为子结构的效能比,表征其耗能效率,其中,W为某一循环加载段输入的总能量;Δres为子结构的残余变形,表征其自复位性能.

表4 SF-CEB子结构耗能及自复位性能
由表4可见,子结构各层的耗能量随加载幅值的增大而增大.相同加载幅值下,一、二层的效能比基本相同.加载幅值为30 mm时,子结构的效能比最低.加载至最大加载幅值时,一、二层的效能比分别为0.53和0.52,子结构耗能效率比装置耗能效率稍低.随加载幅值的增大,子结构的残余变形逐渐增大,但其增长率逐渐减缓;子结构的变形回复率也逐渐增大,至最大加载幅值时,达到90%以上.
子结构较装置的耗能效率低,且无法完全复位.究其原因在于,梁-柱、梁-支撑、柱-支撑等构件之间存在一定的间隙,加载过程中,间隙产生的水平位移使结构刚度减小,而装置几乎未发生轴向变形,即子结构在间隙产生的位移几乎不参与耗能;卸载至荷载为零时,加载时已克服的间隙不能回复到加载前的初始位置,即子结构无法完全复位.
残余层间位移角也是衡量结构复位能力的重要指标.文献[11]规定,结构残余层间位移角θres≤1/300时,结构发生轻微破坏,即当本文中子结构的残余层间位移Δres≤5 mm时,子结构发生轻微破坏.观察表4中的残余层间位移发现,不同加载幅值下,SF-CEB子结构基本都处于轻微破坏状态,说明该子结构具有良好的耗能和复位性能.
6 结论
1) 通过低周反复加载试验,研究了一榀铰接钢框架-自复位耗能支撑子结构的抗震性能.加载过程中,SF-CEB子结构各构件保持弹性,影响该子结构屈服荷载的主要因素是自复位耗能装置核心SMA丝束的面积.采用销轴连接会增大构件之间的间隙,使子结构的初始段刚度偏小,这也是其屈曲位移偏大的主要原因.
2) 随着加载幅值的增加,子结构变形回复率不断增大,子结构保持轻微破坏的状态.可通过改变构件连接的构造方式来减小构件之间的间隙,使结构设计更加合理,性能更加优越.
3) SF-CEB子结构在水平荷载作用下未发生破坏,梁、柱、支撑段始终处于弹性阶段.自复位耗能支撑中,SMA-SCED屈服耗能,效能比为0.53,卸载后结构回复率达90%以上.
4) SF-CEB子结构由于增设了SMA-SCED,具有较高的承载力和延性系数,其耗能和自复位性能较好,故具有一定的推广价值.
