国土资源调查数据地图综合狭长图斑的中剖分处理

徐海江 成晓强 艾廷华

(1. 武汉大学 资源与环境科学学院, 湖北 武汉 430079; 2. 湖北大学 资源环境学院, 湖北 武汉 430062)

0 引言

国土资源大调查成为我国自然资源管理的一项常态化工作,即将结束的第三次国土资源大调查,其成果将为我国国土资源空间格局分析、国土规划治理发挥重要作用。为充分发挥这些信息资源在不同层次的决策规划与应用服务中的作用,对调查成果图进行地图综合缩编产生多比例尺数据库,成为自然资源调查成果数据后处理的关键任务。只有通过综合缩编产生不同级别的自然资源信息,才能针对国家、省、地市及县不同行政级别的战略规划提供适宜、精准的数据支持服务;才能面向多级部门建立立体式的数据服务框架,将横向上的一张图工程拓展为纵向上的金字塔结构;才能建立跨级别数据间的联系,通过级联更新技术保障自然资源调查成果现势性,使调查成果数据有鲜活力。

不同于普通地形图,土地利用数据主要为全覆盖、无重叠、无缝隙分布的多边形图斑,其图斑综合包括空间尺度上的几何特征简化和语义层次上的归并[1]。土地利用图综合前不仅需要考虑图斑几何特征、土地利用性质、权属等语义信息以及图斑邻近关系、所处地理区域环境等上下文环境,综合后的结果也应满足类型的减少、形状的简化、面积平衡的保持、拓扑结构的一致等要求,由此可见土地利用图综合是一个具有复杂约束的决策问题。

土地利用图综合包括对小图斑的剔除、狭长图斑的中轴化、其他图斑的综合化简(邻近图斑融合、图斑边界化简)以及拓扑关系的一致性处理等操作。针对道路、河流等狭长图斑的中轴化处理是土地利用图综合中不可缺少的关键操作之一,常见的中轴化算法包括基于数学形态学的栅格数据综合算子如栅格侵蚀法[2]和基于矢量数据的骨架线提取综合算子如MAT[3]、Delaunay[4]法。基于栅格的综合操作在栅格化过程中存在精度损失问题,其次现有的栅格方法很难精确地对图形进行处理,并且缺乏关注其复杂的语义结构与上下文环境的约束[5]。Delaunay三角网具有“最大最小角”和“空外接圆”的良好性质,可最大限度避免尖锐内角的出现,利用该模型可进行目标间邻近关系的搜索和冲突的检测[6]。艾廷华等[4]通过建立二维空间中约束Delaunay三角网剖分结构探索了其在双线河中轴化及街道中轴线网络模型建立方面的支持作用,并基于此模型提取出街区多边形的街道中轴线[7],算法提取的街道中轴线能够很好地保持原街道的几何特征,证明Delaunay法在处理狭长多边形上具有不可替代的优势。在土地利用图综合处理的过程中,地类图斑中的一些狭长多边形(细长的面状河流、沟渠等)经过综合处理后由原先的二维面状地物生成一维的线状地物,综合前的面面拓扑关系进而转为线面拓扑关系,其中涉及不同要素层间的拓扑一致性改正,这是一个复杂的处理过程。然而现有的研究大多是针对单条独立河流或独立道路做中轴化,没有置入多边形群的上下文中。针对这个问题,江宝得等[8]在狭长图斑与邻近多边形之间的拓扑关系的基础上,将弧段分为三类以完成综合后拓扑一致性的维护,黄剑威等[5]基于圆扩展法对中轴化后的图斑进行拓扑一致性的维护,不可否认,这些方法在一定程度上解决了中轴化后的拓扑一致性问题,然而在应对大数据量的土地利用数据时效率低下,显然这无法满足现实的生产需求。因此,本文在利用约束Delaunay三角网提取出中轴线的基础上,同时给出一种邻域多边形的拓扑一致性处理方法,经实践证明,该方法能够满足现实土地利用图综合的生产需要,在效率与效果上都取得了不错的突破。

1 狭长形图斑的判断与中轴化处理

狭长图斑中轴化的关键在于探测狭长多边形图斑内部到图斑边界线上的等距离点集,这属于空间几何的邻近关系探测问题[9],Delaunay三角网具有“最大最小角”和“空外接圆”的良好性质可以很好地支持空间邻近关系的分析。本文将这一数据结构运用到狭长图斑的中轴线提取中,将图斑边界离散为空间点群,用Delaunay三角形子集存储表达狭长图斑区域,取三角形边线中点作为中轴线的节点,顺次连接,得到图斑的中轴线。

1.1 狭长形图斑的判断

现有的研究中,只是人为主观地将一些细长的河流或道路图斑界定为狭长图斑,缺乏对狭长形图斑的定量化描述,这里在判断图斑用地性质的基础上(第三次国土资源调查中的狭长图斑多为细长河流、道路和沟渠等),给出一种描述区域形态特征的紧凑系数。

相同面积的多边形由于其几何形状的不同,通常反映出不同的紧凑程度,紧凑系数(Cl,compaction index)就是区域形状特征的一种测度量,值的范围在0与1之间,Cl越小表示区域形状越不紧凑,越分散,当区域为圆形时,Cl为1,此时区域形状最为紧凑,反之当Cl趋近于0时,区域形状趋近于一条直线。常用的紧凑系数公式可分为基于长轴的形状率法,基于周长的圆形率法,以及基于最小外接圆的紧凑度法。由于圆形率紧凑系数参数的易获得性,故而这里将其作为描述多边形图斑形状特征的度量,公式(1)中S为图斑面积,L为多边形图斑边界周长。

(1)

实际上狭长图斑宽度并不是一成不变的,如图1所示反映了具有多条支流存在的河流水系的狭长图斑,在对该类图斑进行中轴化的过程中,不能将其单独看作一个整体处理,需要分而治之,独立考虑每个支流的宽度以决定是否做中轴化处理,在后面的章节中将仔细讨论此类图斑的处理方法。

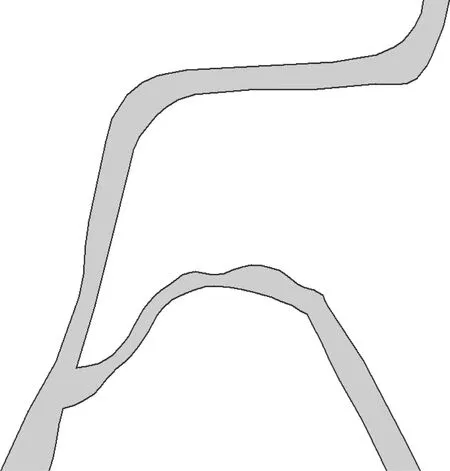
图1 不等宽多分支河流

1.2 中轴线网络图的构建

为提取狭长图斑中轴线,需将图斑边界离散为空间点群,在图斑覆盖区域构建约束Delaunay三角网。边边相连的三角网构成了狭长图斑内部空间的剖分结构,如图2所示,根据有效邻接三角形个数,可将其细分为三类[4]:出现在狭长图斑出口处,仅有一条边有邻近三角形为Ⅰ类;两边有邻接三角形为Ⅱ类,该类三角形为三角网骨干结构,描述了中轴线的延展方向;三边均有邻接三角形为Ⅲ类,常出现在中轴线分支交汇处。

图2 三类三角形及其中轴线连接

Delaunay三角网中三角形的边可看作是狭长多边形图斑边界上一点到其他边界点的邻近跨接,因而可将跨接边的中点看作多边形在该区域的中心。顺次连接邻接三角形边的中点,便可反映出狭长多边形图斑在一维空间上的延展趋势,即图斑中轴线。具体提取思想如下:由Ⅰ类和Ⅲ类三角形出发沿着Ⅱ类三角形搜索,终止于Ⅰ类或Ⅲ类三角形,当所有的Ⅰ类三角形搜索过一次,所有的Ⅲ类三角形作为出发或终止搜索过三次时,中轴线网络图即构建完成,构建结果如图3所示。

图3 中轴线网络示意图

1.3 中轴线的后处理

在1.2中提到,狭长图斑的宽度是多变的,需要确定图斑的每个分支是否需要中轴化,即判断每个分支的宽度是否满足最小上图宽度的要求。

设第i个分支的中轴线由系列点{Pij}(j=1,2,3…)构成,分支L1、L2与L3构成了如图4所示的网络图,现求L1分支的中轴线宽度,对I类三角形做P1P2垂直平分线N11N12;对Ⅱ类三角形作P3P4垂线N31N32;对Ⅲ类三角形,由于有3条中轴线,对该分支中轴线所在的边OP5作垂直平分线N51N52, 按照上述方法,对该分支每个三角形中的中轴线PiPi+1,计算该段中轴线对应的宽度Wi,则该段中轴线的加权平均值可表示如下:

图4 各类三角形对应的宽度

(2)

式中,|PiPi+1|为三角形中轴线的长度,|Ni1Ni2|为对应的宽度值,L为该段中轴线长度。

针对每段中轴线分支,计算每个分支的平均宽度,若宽度小于目标比例尺下的最小上图宽度,则该分支需要进行中轴化处理以代替原先的多边形表达。

2 邻域多边形拓扑一致性处理

为了解决中轴化后图层间的拓扑不一致问题,需要把原狭长图斑置入多边形群的上下文中,找出相邻的多边形地块,向提取出的中轴线作扩张处理来填补局部的空洞区域,以此维护拓扑关系的一致性。本文将这一扩张的过程分成“剖分”与“归并”两步,在“剖分”阶段,计算原狭长图斑与邻近图斑共享拓扑节点在中轴线上对应的剖分点,共享拓扑节点与剖分点的连线与对应的边界弧段和分割的中轴线线段共同构成剖分区域,从而完成对狭长图斑的剖分处理。在“归并”阶段,计算剖分图斑与邻近多边形的综合邻近度,将剖分图斑合并到综合邻近度最高的邻域多边形中,从而维护综合后拓扑关系的一致性。

狭长图斑中轴化处理后,图斑的局域拓扑关系发生了变化,狭长图斑区域出现了空洞,原先的面-面拓扑相邻的空间关系变为了线-面相离的拓扑关系。特别的,还可能存在其他比较复杂的拓扑变化情况,当两个不满足最小上图宽度的狭长图斑拓扑相邻(如农村道路与沟渠相邻),若直接对两个狭长图斑单独进行中轴化,拓扑关系由原先面-面相邻变为线-线平行、线-面相离及面-面相离,面与线之间、线与线之间存在着空洞区域。解决方法是,先将这2个图斑合并,提取合并后的图斑中轴线,同时维护中轴线两侧的拓扑一致性。

地理信息系统(geographic information system，GIS)中的面状地理要素一般都是用拓扑模型存储的,通过唯一ID标识面、弧段和节点,弧段与弧段之间通过节点关联,多边形由弧段集构成,弧段之间由节点关联,弧段与节点存储空间位置信息,而多边形只存储关联的弧段ID序列。由于多边形间的共享弧段只存储1次,同时在拓扑模型中,面、弧段和节点之间的拓扑关系已经预先存储了,因而容易获取要素之间的拓扑关系。基于这样的拓扑数据模型,本文提出了狭长图斑的“剖分”思想:以中轴线为狭长图斑分割线,以邻近图斑与狭长图斑的拓扑节点为“剖分”的参考点,在中轴线上寻找对应的剖分点。

如图5(a)所示,F为待中轴化的狭长图斑,与图斑A、B、C、D及E拓扑邻近,其中弧段Arc1为图斑A、F之间的共享弧段,T1、T2为共享拓扑节点。由于中轴化之后,原先的狭长的图斑从图层中删除,生成了空洞区域,需要将邻近图斑向中轴线方向扩张以填补空洞,以确定邻近图斑的增长区域,即对应狭长图斑中的剖分地块。在地图综合中,为了延续地图从大比例尺到小比例尺的可读性与可理解性,扩张后的邻近图斑需要延续原图斑的形态特征,扩张区域不能影响对于邻近图斑的判读识别,最有效的策略是以原共享弧段为扩张起始边,在中轴线上确定距离共享节点最近的剖分点,以中轴线剖分点之间的线段作为最终的扩张终止边。拓扑节点T1在中轴线上对应的剖分点为Q1(若从T1至中轴线的垂足Q1,当Q1落在中轴线上,剖分点为Q1,否则为中轴线上距离Q1距离最近的点),T2在中轴线上对应的剖分点为Q2,剖分点与对应拓扑节点的连线T1Q1、中轴线上剖分点之间的线段Q1Q2、狭长图斑与邻近图斑之间的共享弧段Arc1以及T2Q2共同构成了狭长图斑的剖分地块F1。对狭长图斑的所有拓扑节点,基于这样的剖分思想,将原狭长图斑剖分为细小地块。

图5 狭长图斑的剖分与归并示意图

特别的,在狭长图斑的出入口处的拓扑点即对应I类三角形的顶点,按照上面的剖分方法易产生末端的碎片式的小图斑。因此,在剖分之前,搜索出所有的I类三角形对应的“出边”或“入边”,将该边与中轴线的交点作为剖分点,同时从狭长图斑拓扑节点集{Ti}中排除该类拓扑点。

对狭长图斑进行剖分后,根据剖分地块与邻近地块的邻近度确定其归并图斑。在土地利用图中,两图斑间的邻近程度既要考虑语义上的邻近性,又要考虑空间位置上的差异性[10],将剖分地块合并到最邻近邻域图斑中,以填补中轴化后生成的空洞,达到拓扑一致性维护的目的。如图5(b)为图斑剖分后的归并结果示意图。

3 “三调”数据综合中应用实验

相较二调的西安80坐标系,第三次全国土地调查数据采用的是国家2000国家大地坐标系,基础底图的影像精度由原来的2.5 m提升到1 m。除了空间位置更加精确,内容也更加精细化,二级类标准由原来的57级增加到73级。在11个一级类中,涉及需要中轴化的图斑类型有耕地、交通运输用地、水域及水利设施用地以及其他土地中的田坎。以1∶1万到1∶5万的土地利用图综合为例,在ArcGIS10.2平台上用C#编制了实验程序,采用的实验数据为珠海市某区域第三次土地调查成果数据。利用本文提出的方法,首先识别出区域的狭长图斑,对狭长图斑区域构建约束Delaunay三角网,计算出每个分支的平均宽度,对小于最小上图宽度的分支提取出中轴线,以中轴线为分隔线,以狭长图斑与邻近图斑的共享拓扑点为参考点,寻找对应落在中轴线上的剖分点,将剖分后的狭长图斑按综合邻近度归并到最邻近图斑中去。对于一些特殊情况,如两个长边接壤的狭长图斑,需按照本文方法优先进行中轴化处理。此外,对于作为境界一部分的狭长图斑,将境界一侧的边界作为中轴化后的中轴线,同时维护境界内侧拓扑关系的一致性。

本文所选实验区内的土地利用数据共有135条狭长图斑,其中有8条细长河流,127条道路,按照本文所述方法提取中轴线。如图6(a)为选取的部分区域提取前示意图,其中的狭长图斑已用深色凸显,图6(b)为提取后的结果,其点画线部分为原图斑边界。提取的中轴线能够很好保持原狭长图斑的延展特征,利用拓扑检查工具检查后,中轴化的图斑不存在空洞及重叠区域,拓扑关系的一致性也得到了很好的维护。

图6 中轴化前后对比图

4 结束语

对自然资源调查成果进行综合缩编是多比例尺数据库建设的关键任务,狭长图斑的中轴化是其中的重要操作之一,中轴化前后拓扑关系的一致性维护涉及不同要素层之间的协调统一,是中轴化操作中的难点问题。本文利用约束Delaunay三角形子集存储表达狭长图斑区域,以三种类型三角形边线中点作为中轴线的节点,顺次连接得到狭长图斑的一维表达,将狭长图斑各个分支的平均宽度作为分支是否需要中轴化的衡量标准。此外,针对狭长图斑中轴化后拓扑关系的改正,提出了“剖分”与“归并”的解决方案来模拟邻近图斑的扩张过程。在“剖分”阶段,计算原狭长图斑与邻近图斑共享拓扑节点在中轴线上对应的剖分点对狭长图斑进行剖分处理。在“归并”阶段,通过比较剖分地块与邻近多边形的综合邻近度,将剖分图斑合并到邻近度最高的邻域多边形中,以此维护综合后拓扑关系的一致性。经第三次国土资源调查成果检验,本文的中轴线提取方法可以有效保持原狭长图斑的延展特性,中轴化后的拓扑关系得到了很好的维护。能够满足土地利用图综合实际生产的需要。

本文的剖分方法是建立在拓扑数据结构上的操作,忽视了对狭长图斑周围语义类型的考虑,此外,如何在剖分过程中有效维持邻近多边形图斑的形状特征,减少归并过程中“尖角”等合并不合理现象的出现,这将是以后需要关注的研究方向。