激光点云粗配准方法实验对比与分析

崔志婷 李彩林 王志勇 苏本娅 王佳文 孙延坤

(山东理工大学 建筑工程学院, 山东 淄博 255000)

0 引言

为了实现对被测物体的整体覆盖,进行激光扫描时需要多点架站,每站点云具有独立的坐标系,通过将不同视角下的激光点云进行拼合,实现各站点云坐标系的统一,完成点云的配准。点云配准是点云处理流程中的重要步骤,更是逆向工程、计算机视觉等领域中进行三维重建的关键问题,其配准的效率和精度对工程整体有十分重要的影响。

点云配准通过寻找不同点云间的同名特征来计算他们之间的变换矩阵,然后将点云拼接在同一坐标系下。配准算法分为粗配准和精配准,点云粗配准使两组点云数据尽可能接近,减小两个点云模型间的差异,为精配准提供良好的初值,提高配准效率和精度。粗配准方法有基于遗传算法(Genetic Algorithm, GA)[1]、基于特征以及全局配准的方法,同时还可以通过点云处理软件进行粗配准。

ZHU等提出利用GA对部分重叠范围扫描进行对偶配准的有效方法,利用可靠的成对配准结果计算初始参数,但该算法效率较低[2-3]。基于特征的粗配准首先是根据局部特征描述符计算点的特征,然后根据特征对点云进行匹配,确定点的对应关系后进而对变换参数进行求解[4-5]。SUN等提出了一种判别性强的局部形状描述符—区域曲率图(RCM),采用基于RCM子区域的搜索匹配策略寻找三维对应点,利用几何一致性实现粗配准,具有较高的配准效率[6]。RUSU等提出通过三维形状描述符计算特征点的几何特征,将来自不同点云的具有最相似特征的点对识别为对应点,求解变换参数,这种算法容易受到噪声点的干扰[7]。全局配准算法中,有基于随机抽样一致算法(Random Samle Consensus, RANSAC)框架的方法,该方法利用点云数据间的重叠区域确定对应点,根据对应点求解待匹配点云间的刚体变换关系,通过对候选基重复投票,最后将概率最高的候选基确定为最优解,但该算法稳定性不高,容易匹配错误的对应点[8]。ZHOU等提出一种快速全局配准算法,该算法对点云表面的点进行配准,不需要初始化,运行速度较快[9]。AIGER等提出了四点全等集算法4PCS(4-Points Congruent Sets),此算法的理论基础在于共面4点对的仿射不变性,通过使用广域基,将搜索复杂度降低,对噪声和离群点有较好的鲁棒性[10]。MELLADO等提出超级四点全等集算法(Super 4-Points Congruent Sets,Super4PCS),该算法允许任意位姿的扫描,而且算法时间复杂度是线性的,通过在目标点云中进行光栅化的网格划分来实现点对的快速提取,同时利用角度约束来减少无效点对的产生,提高了整体点云的配准精度和效率[11]。点云还可以通过Geomagic Studio、RiSCAN PRO等点云处理软件进行粗配准。

本文分别利用Super4PCS算法、4PCS算法和点云处理软件Geomagic Studio12,对四组激光点云数据进行配准实验,并对配准结果进行对比分析,得出他们各自的适用性。

1 4PCS算法

4PCS的算法原理为:首先在源点云P中随机选择3个点,形成一个面,并依据共面不共线原则选择第4个点,从而组成一个共面的4点基B,然后在目标点云Q中找到所有可能与B相似的全等的4点子集S,对于集合S中的每一个元素Si,利用其与B的对应关系求得刚性变换矩阵Ti,使得B与Si的距离最小,然后根据(Largest Common Pointset,LCP)方法求得所有的最优值并以此作为此轮迭代的最佳变换。最后将最佳变换矩阵T应用到源点云P中,实现点云粗配准。

在点云数据中的任意共面的4个点可以确定两个点对,4点集B={a,b,c,d}可以称为一组基。如图1所示,将每组基的表示量定义为:r1、r2、L1、L2,其中r1、r2为比例因子,其在点云旋转和平移变化中具有仿射不变性,L1、L2为点距,如果两组基的所有表示量都相等,则这两组基具有一致性,即对应的一致全等4点。r1、r2、L1、L2的具体表示如图1所示。

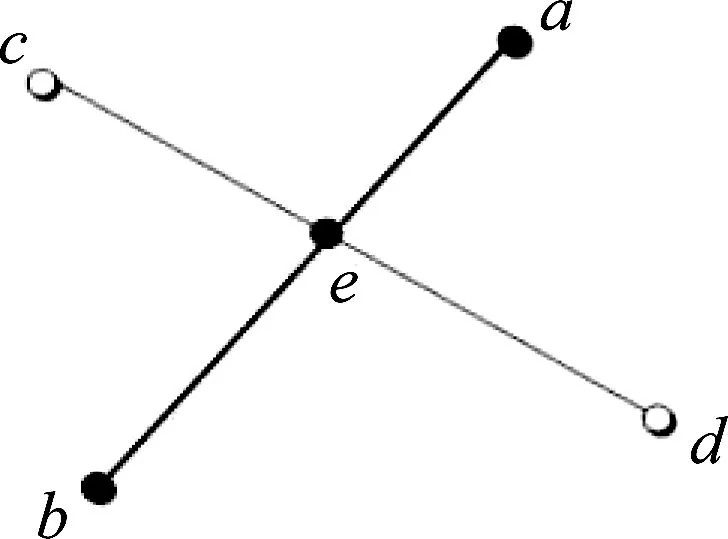
图1 四点基

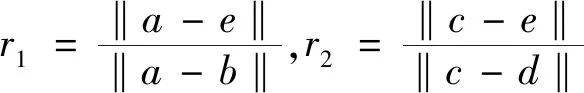
(1)

L1=‖a-b‖,L2=‖c-d‖

(2)

2 Super4PCS算法

Super4PCS算法允许任意位姿的点云进行配准,能够自动删除有误点对并对有效点对快速提取,实现点云的快速配准。Super4PCS算法的基本原理为:

(1)在源点云内选取基时,要遵循距离最大化原则,即保证点与点之间的距离最大化但又不超过某一阈值,而这一阈值由重叠率f来确定,同时还要采用三加一策略,即先在可能为重叠区域的点云表面选择3个不同的点,第4个点由共面不共线原则进行选取,由此共面4点组成一个基B={Pa,Pb,Pc,Pd}。确定基B后,可以得到相应的比例r1、r2,以及两点之间的距离d1、d2,其具体表示为:

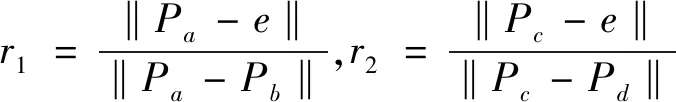
(3)

d1=‖Pa-Pb‖,d2=‖Pc-Pd‖

(4)

(2)先在目标点云Q中确定集合S1与S2。在目标点云Q中以每一点qi为球心,并分别以R=d1±ε和R=d2±ε为半径画球。qi与在[d1-ε,d1+ε]范围内的点即为点对集合S1,而qi与[d2-ε,d2+ε]范围内的点对为集合S2。同时建立一个单位尺寸为ε的三维网格G将点云表面进行栅格化。

(3)源点云P中选定的基如图2(a)所示,在目标点云Q中存在与其对应的点集但同时也存在错误的点集{qa,qb,qc',qd'},如图2(b)所示。在目标点云Q中提取与基B对应的4点集。遍历点对集合S1和S2中所有的候选点对,根据交比一致性计算所有的交叉节点e,并存储在网格G中。依据基B中两对应点对的夹角为θ,在网格G中提取出节点近似相等,同时两点对之间的连线夹角近似等于θ,其误差范围在ξ内的4点基进行匹配。

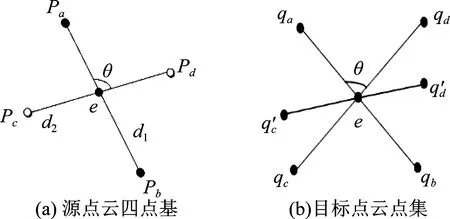
图2 Super4PCS示意图

(4)在点云Q中所有满足条件的与基B对应的四点集合U={U1,U2,…,Un},求出基B与每一个Ui之间的变换矩阵,通过比较最大化公共点集LCP选择其中配准精度最高的变换矩阵进行全局变换。

3 实验与分析

3.1 实验数据

本文采用激光扫描仪Z+F IMAGER®5010C分别对佛像和青铜器进行实体三维扫描,如图3(a)、(b)所示,获取的佛像三维点云数据特征较为明显;如图3(c)所示,青铜器点云特征显著且带有噪声。同时利用三维激光扫描仪RIEGL VZ-400对孔子雕像进行扫描,获取的三维点云数据如图3(d)所示。表1为各站点云数。

图3 相邻两站激光点云数据

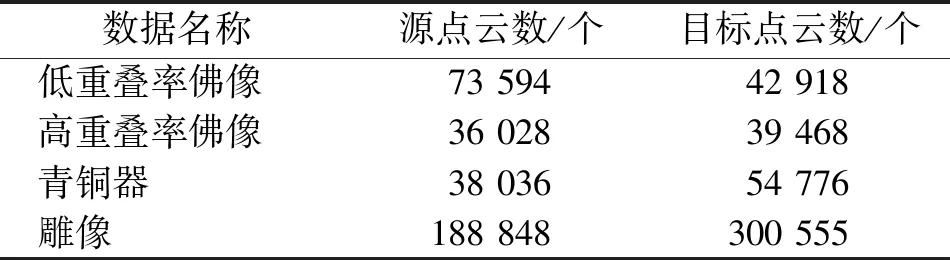
表1 各站点云数

3.2 实验结果与分析

实验在相同的运行配置环境下进行,分别对低重叠率佛像、高重叠率佛像、青铜器和雕像四种数据集进行配准,对比分析Super4PCS、4PCS算法以及软件Geomagic Studio 12配准结果。图4为Super4PCS算法配准效果图,图5为4PCS算法配准效果图,图6为软件Geomagic Studio 12配准效果图。本文通过计算均方根误差(Root Mean Square Error, RMSE)作为配准精度指标,RMSE为源点云和目标点云间的平均距离,并对3种方法的配准时间进行统计分析。结果如表2所示。

图4 Super4PCS算法配准效果图

图5 4PCS算法配准效果图

图6 软件配准效果图

根据配准效果图4～6和表2可知:

(1)对于低重叠率佛像点云来说,由于相邻两站点云重叠率过低,相似特征少,不利于点云配准。由点云配准效果图可知,Super4PCS算法和4PCS算法在配准低重叠率点云时结果均出现较大偏差,软件配准低重叠率点云则结果较好。Super4PCS算法和4PCS算法对点云重叠率有较高要求,因此在配准低重叠率点云数据时可以选择软件配准等其他有效方法。

(2)对于高重叠率佛像点云,重叠区域相似特征多,有利于点云数据融合。软件配准精度高于4PCS算法的配准精度,Super4PCS算法点云配准效果最好。由表2可知,Super4PCS算法的配准精度和效率明显优于其他两种方法。

(3)对于青铜器点云,具有明显的噪声点,噪声点在一定程度上影响配准精度和时间。由配准效果图可以看出,对存在噪声点的两站点云,4PCS算法和软件配准方法的配准效果都存在明显偏差,Super4PCS算法配准效果较好。由表2可知,软件配准点云结果精度高于4PCS算法点云配准精度,Super4PCS算法的配准精度和效率优于其他两种方法,具有更高的鲁棒性。

(4)对于雕像点云,点云数据量明显增多,且相邻两站点云数差别较大,相比于其他点云数据,其形状更为复杂。从配准效果图可以看出,4PCS算法配准后两站点云有明显的左右偏差,软件配准则有上下偏差,Super4PCS算法配准效果最好。由表2可知,4PCS算法的点云配准精度高于软件配准精度,相比于这两种方法,Super4PCS算法配准精度更高且更高效。

表2 点云配准效果评估

总体来看,对于特征多、重叠率高的点云模型,3种方法都可以较好的完成配准。对于重叠率较低的点云数据,Super4PCS算法和4PCS算法不能实现点云的有效拼接,可以选择其他有效方法。除低重叠率点云数据外,Super4PCS算法的配准精度和效率最高,4PCS算法的效率其次,软件Geomagic Studio 12的点云配准精度和时间受人为因素的影响,具有不稳定性。

4 结束语

本文通过运用Super4PCS、4PCS算法和软件Geomagic Studio 12对四组点云数据进行配准实验,统计实验结果并进行了比较分析。实验结果表明,Super4PCS效率最快,配准效果最好,对噪声有较好的抵抗力,不适用于低重叠率点云模型配准;4PCS配准效率较快,对噪声的抗干扰能力较差,同样不适用于低重叠率点云配准;软件Geomagic Studio 12效率最慢,适用于各种情况的点云配准,配准精度受人为因素的影响。点云配准时,可以依据数据的特点选取合适的方法。

实验中采用的算法都是原始的经典自动粗配准方法,不少学者对这些算法进行了改进以提高配准效率和精度。对这些改进算法进行不同条件下的实验对比与分析,将是下一步的研究工作。