面向雷达数字化设计与仿真的电子干扰建模方法研究

卢 冀 陈皓晖 李万玉

(1.西安电子工程研究所 西安 710100;2.中国人民解放军32382部队 北京 100071)

0 引言

仿真雷达模型同目标、杂波、电子干扰等模型的相互作用是雷达数字化设计与仿真系统的核心功能[1-3]，其中电子干扰模拟是这一雷达技术领域的竞争热点问题[4-5]，探索适用于雷达数字化设计与仿真系统的电子干扰建模方法，面临着新的问题：

1)雷达电子干扰波形参数如何基于统一的雷达模型同目标、杂波、电子战等相互作用模型的接口[2-3]进行设计，需描述噪声等覆盖类干扰和假目标等欺骗类干扰的信号参数，以通过仿真真实且高效地反映雷达电子干扰造成的被干扰雷达回波波形的变化。

2)雷达电子干扰波形如何考虑其在空间的传播效应，需描述主要的传播路径，并分别计算不同路径下电子干扰波形参数的变化，以真实有效地模拟信号的空间传播特性。

3)雷达电子干扰波形到达雷达的角度计算问题，需根据干扰机和雷达的空间位置和姿态角度计算干扰波形到达雷达的角度，以通过电子干扰到达角模拟自卫或远距离的干扰方式，且便于雷达模型计算回波信号的复功率等参数。

本文将围绕上述问题，系统性地探索雷达数字化设计与仿真中的电子干扰模拟技术和具体实现方法，为数字化雷达电子干扰模拟的实现与技术发展起到抛砖引玉的作用。

1 总体设计

电子干扰模型的功能框图见图1所示，主要包括雷达模型、信号传输和电子干扰等数字化模型，本文以电子干扰信号产生、传输及到达雷达入手研究电子干扰波形的产生、传输及到达雷达的变化，采用的波形参数不仅可用于雷达模型对回波接收与处理的仿真，而且能用于生成干扰回波信号。

图1 电子干扰模型功能框图

波形参数是雷达模型同电子干扰模型，以及目标、杂波等数字模型进行交互的接口，需要根据雷达模型进行统一描述[1-3]，见表1所列。电子干扰建模的本质就是考虑表1所列波形参数的变化。

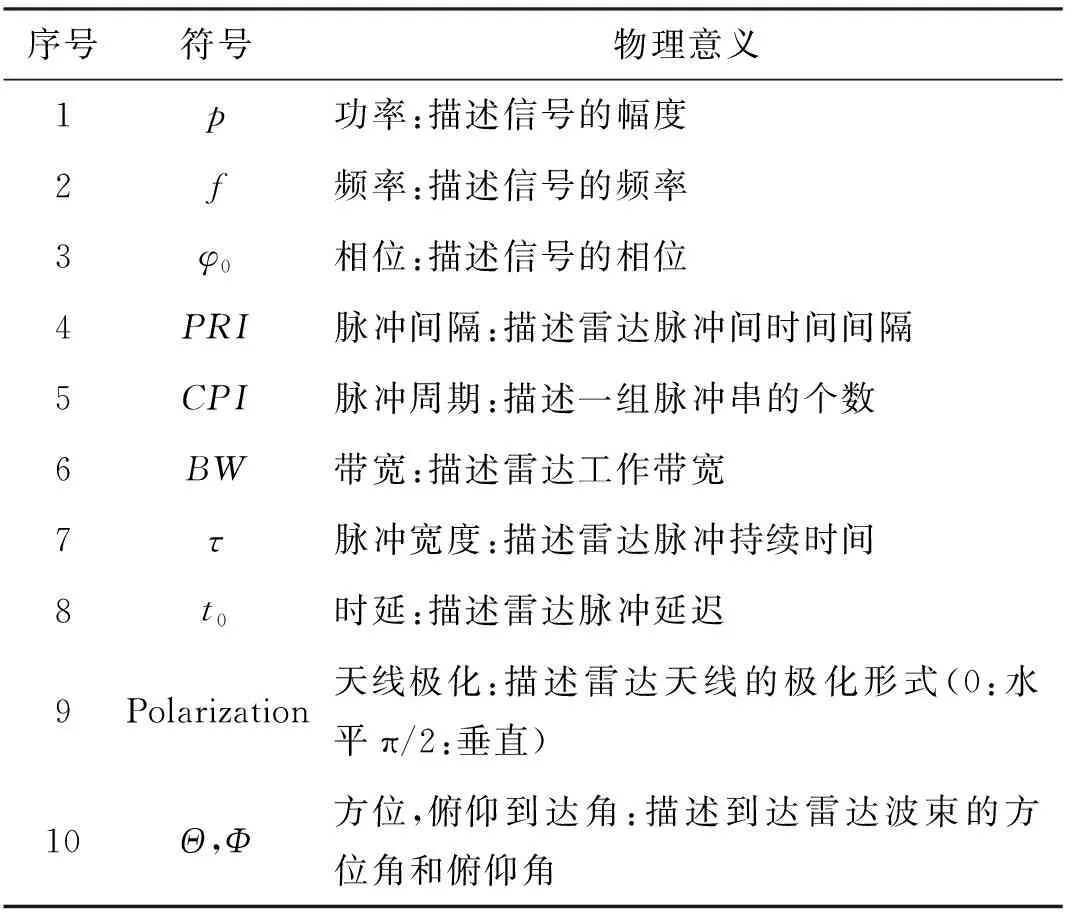
表1 信号波形参数

电子干扰信号的产生，将根据覆盖和欺骗干扰的信号形式，产生波形参数中p、f、φ0、t0、PRI、BW和τ的变化或描述，信号的传输将根据直达路径和多路径传播特点，计算p、f、φ0、t0的变化，信号的到达在直达路径和多路径的情况下，计算到达波束的Θ和Φ。

航迹信息是数字化设计与仿真系统中透明的信息，方便设计者利用航迹信息较真实的模拟因干扰机、雷达以及目标位置和姿态变化导致的波形参数的变化，雷达、干扰机和目标的航迹包括雷达位置(Xr,Yr,Zr)、干扰机位置(Xj,Yj,Zj)和目标位置(Xt,Yt,Zt)，以及雷达姿态(θj,φj,ψj)、干扰机姿态(θr,φr,ψr)和目标姿态(θt,φt,ψt)。

2 具体实现

2.1 信号产生

电子干扰信号主要通过覆盖方式或欺骗方式降低或替代有效目标的信噪比，导致雷达目标检测出错，进而影响后续测量、跟踪、识别等功能。电子干扰信号样式多样化，很难一一列举，本文针对典型有源干扰的覆盖类和欺骗类干扰浅析其数字化参数产生方法，此外，文献[3]中给出了一种箔条干扰的数字化建模方法。

噪声信号参数与雷达发射波形参数是相似的，可以用表1描述的信号波形参数来描述噪声信号波形参数，噪声信号的波形参数主要跟噪声峰值功率P，起始频率F，相位Φ，带宽B，间断周期TI和占空比Dc相关。显然，由表1描述的信号波形参数与P、F、Φ、B，TI和Dc的对应关系见表2所列。

表2 噪声信号波形参数说明

欺骗干扰信号参数与雷达发射波形参数乃至目标回波波形参数是相关的，可以认为欺骗干扰信号参数的PRI、CPI、BW、τ(相对速率造成的变化很小)同雷达信号波形参数相同，只考虑p、f、φ0和t0发生的变化。数字化仿真系统产生不仅可以采用传统方式对p、f、φ0和t0进行调制产生距离、速度及距离速度联合拖引干扰，密集假目标等干扰信号，还可以通过复制目标模型的方式，增加目标模型并赋予其新航迹后，通过目标的实时位置与姿态更新，产生逼真的假目标干扰信号。

不妨设雷达相对目标回波参数功率、频率、相位和时延分别为P、F、Φ和T，则通过参数调制方式生成的欺骗干扰信号参数描述见表3所示。拖引干扰一般分为起始期，拖引期和停止期三个时间段，起始期内p如表3所列变化，拖引期内p、f、φ0和t0变化如表3所列，停止期内停止干扰信号产生。

表3 参数调制方式干扰信号参数

复制目标模型的方式可以更逼真地模拟假目标，在数字化仿真系统中，假目标干扰信号波形的p和φ0由JSR和目标RCS确定，f和t0因航迹改变导致的变化按照信号传播小节中方法进行计算，新航迹可根据拖引距离和速度、雷达距离门和多普勒门、目标运动学或动力学方程进行计算。p和φ0分别为

(1)

φ0=φ

(2)

其中σ和φ是目标RCS描述σejφ的幅度和相位，σ和φ可由频率、天线极化、雷达波束方位和俯仰到达角确定[2]，其计算亦可参考2.3小节方法，p和φ0也因假目标位置和姿态的变化而变化。

2.2 信号传播

电磁波信号可通过直视、反射、折射、绕射、衍射等方式传输，传输过程中单站雷达信号的变化主要是由直视和反射方式的直达路径和单跳多路径的衰落引起[4]，主要考虑直达路径和多路径对波形参数p、f、φ0和t0变化，即p的衰减和t0、f、φ0的变化，分别记为Δdlos，Δtlos，Δfdlos，Δplos和Δdmp，Δtmp，Δfdmp，Δpmp。已知干扰机和被干扰雷达的坐标分别为(Xj,Yj,Zj)和(Xr,Yr,Zr)，易得直达路径功率衰减Δdlos可描述为

Δdlos=4πR2

(3)

其中R为干扰机到雷达的距离，R可描述为

(4)

Δtlos可描述为

(5)

其中c表示光速。Δfdlos可描述为

(6)

其中Ts表示仿真系统数据采样时间间隔，f是干扰信号中心频率。Δplos可描述为

(7)

多路径传输中，Δdmp，Δtmp，Δfdmp和Δpmp计算方法与直达路径相同，因电磁波信号在地球表面进行了反射，Δdmp和Δpmp受电磁反射参数的影响，同时在计算过程中传输距离Rmp也需由地球模型[7]进行计算，那么Δdmp可描述为

Δdmp=Cd·4πRmp2

(8)

其中Rmp=R1+R2，R1表示干扰机到反射点的距离，那么

(9)

其中Re为地球半径距离，φ1为R1对应的地球球心角，则

(10)

其中Rg为干扰机和雷达对应的地面表面距离，则

(11)

R2表示反射点到雷达的距离，那么

(12)

φ2为R2对应的地球球心角，则

(13)

Cd为多路径功率衰减系数，其计算方式[4]为

Cd=Г2=(Г0D(ρs+ρd))2

(14)

其中Г为Fresnel多路径反射系数，Г0为光滑地面反射系数，描述为

(15)

其中εc为复介电常数，有[5]

εc=εr-j60λσe

(16)

εr和σe分别为介电常数和电导率，可根据地表类型查表获得[4]，λ为信号波长，α为干扰机多径信号的擦地角，描述为

(17)

式(14)中D为地面散射因子，可描述为

(18)

式(14)中ρs为镜面反射粗糙因子，描述为

(19)

其中Vw表示风速。式(14)中ρd为漫散射粗糙因子，描述为

(20)

综合式(15)、式(18)和式(19)代入式(14)求的Cd，同式(9)和式(12)得到的R1和R2，代入式(8)可得Δdmp，Δtmp可描述为

(21)

Δfdmp可描述为

(22)

其中fvt表示地表是树木和海水时由树木和海水运动造成的扰动频移，则

(23)

其中rand[n,m]均值为n，方差为m的高斯分布变量。Δpmp可描述为

(24)

其中Cp为多路径相位变化系数，其计算方式[4]为

(25)

其中pvt表示地表是树木和海水时由树木和海水运动造成的相位的扰动变化，则

pvt=2πfvtTc

(26)

其中Tc表示仿真系统设置的相位变化的相关时间。

2.3 到达角

已知干扰机天线和被干扰雷达天线的x,y,z轴位置坐标分别为(Xj,Yj,Zj)和(Xr,Yr,Zr)，方位、俯仰、横滚的姿态角分别为(θj,φj,ψj)和(θr,φr,

ψr)，干扰机天线波束直达雷达的方位和俯仰到达角分别为Θd和Φd，则Θd和Φd分别描述为

(27)

(28)

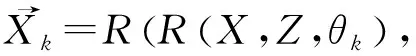
(29)

(30)

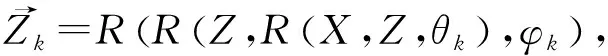
(31)

其中R(U,V,ω)表示向量U绕向量V旋转ω角度后得到的新向量，则

R(U,V,ω)=(U×V)sinω+
(1-cosω)(U·V)·V+Ucosω

(32)

R()|n，n=1,2,3表示三维向量R()的第n维的值。

干扰机天线波束单跳反射多径到达雷达的方位和俯仰到达角分别为Θm和Φm，显然，Θm和Θd相同，Θm可描述为

Θm=Θd

(33)

Φm可由式(17)描述的擦地角计算，并将式(31)结果代入式(17)，则Φm描述为

(34)

经坐标变换，R1描述为

(35)

其中φ1描述为

(36)

其中Rg描述为

(37)

直达波路径通过式(27)和式(28)计算到达角，单跳多路径可通过式(33)和式(34)计算其到达角，根据到达角，结合天线波束指向和方向图即可获得干扰信号的复功率。

3 实现结果

图2显示了通过Matlab实现的数字化雷达电子干扰模型的顶层模块，通过Jammer、Path和AOA三个模块实现了干扰生成、干扰信号传输和干扰到达角的计算。

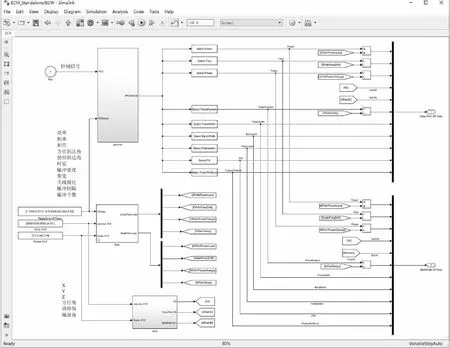
图2 数字化雷达电子干扰模型

图3显示了采用白噪声覆盖干扰实现框图，由表2知，白噪声参数可分别通过调幅、调频和调相方式生成。仿真时长为20 s，采样时间间隔为0.005 s，仿真了白噪声典型参数的生成结果。图4(a)显示了JSR为6 dB，输入功率为1时通过均值为0、方差为1的高斯分布随机数产生的调幅白噪声的幅度变化，图4(b)显示了输入频率为33 GHz时通过均值为0、方差为1的高斯分布随机数且KFm为20时产生的调频白噪声的频率变化，图4(c)显示了输入相位为0时通过均值为0、方差为1的高斯分布随机数且KPm为20时产生的调相白噪声的相位变化。

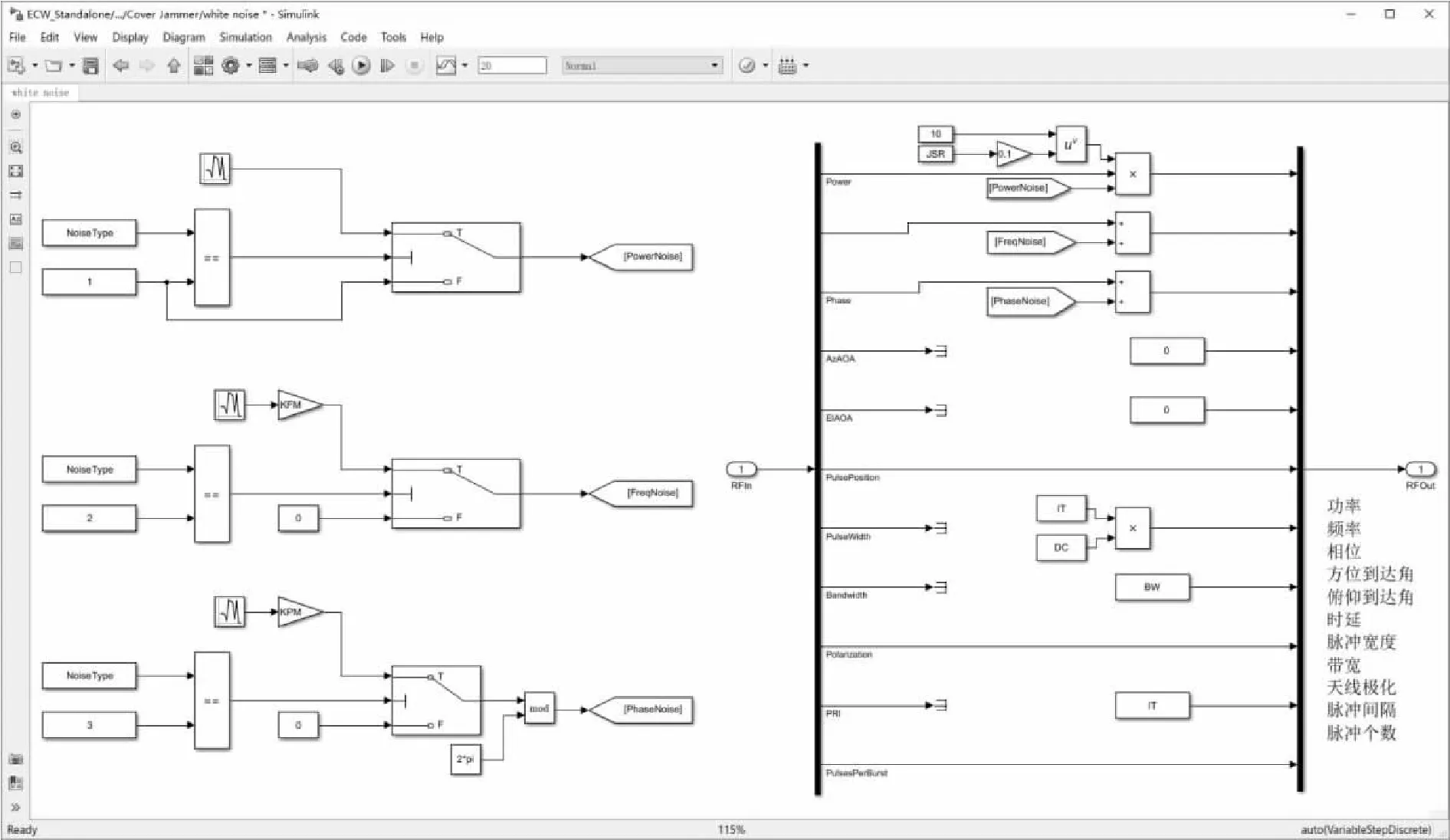
图3 覆盖式白噪声干扰

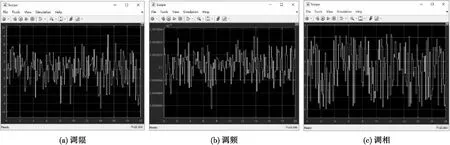
图4 白噪声干扰典型参数仿真结果

图5显示了欺骗干扰的实现框图，由表3知，欺骗干扰主要影响波形的幅度、频率、相位和时延。针对距离和速度门联合拖引干扰，设仿真时长为100 s，采样时间间隔为0.005 s，无干扰信号幅度为1，频率为33 G，相位和起始时延为0，JSR=6 dB，干扰起始期，拖引期和停止期时间长度分别为2 s,5 s和3 s，距离门500 m，速度100 m/s, 加速度50 m/s2，速度门用多普勒表示，范围设为[2 kHz, 50 kHz]，频率加速度20 kHz/s，图6(a)至图6(d)分别显示了该干扰幅度、频率、相位及时延的变化，其变化规律与论文设计一致。

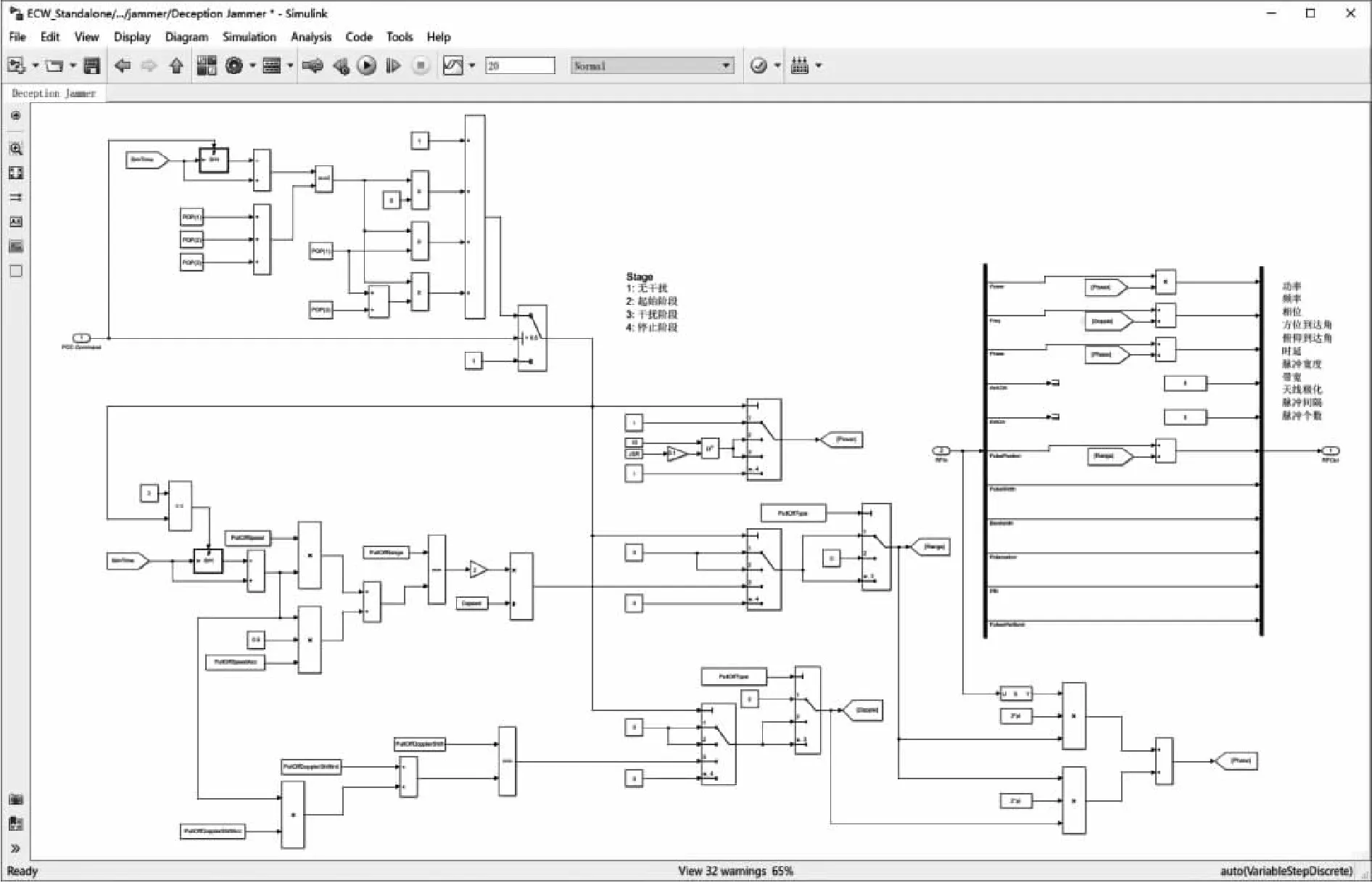
图5 欺骗干扰的实现框图

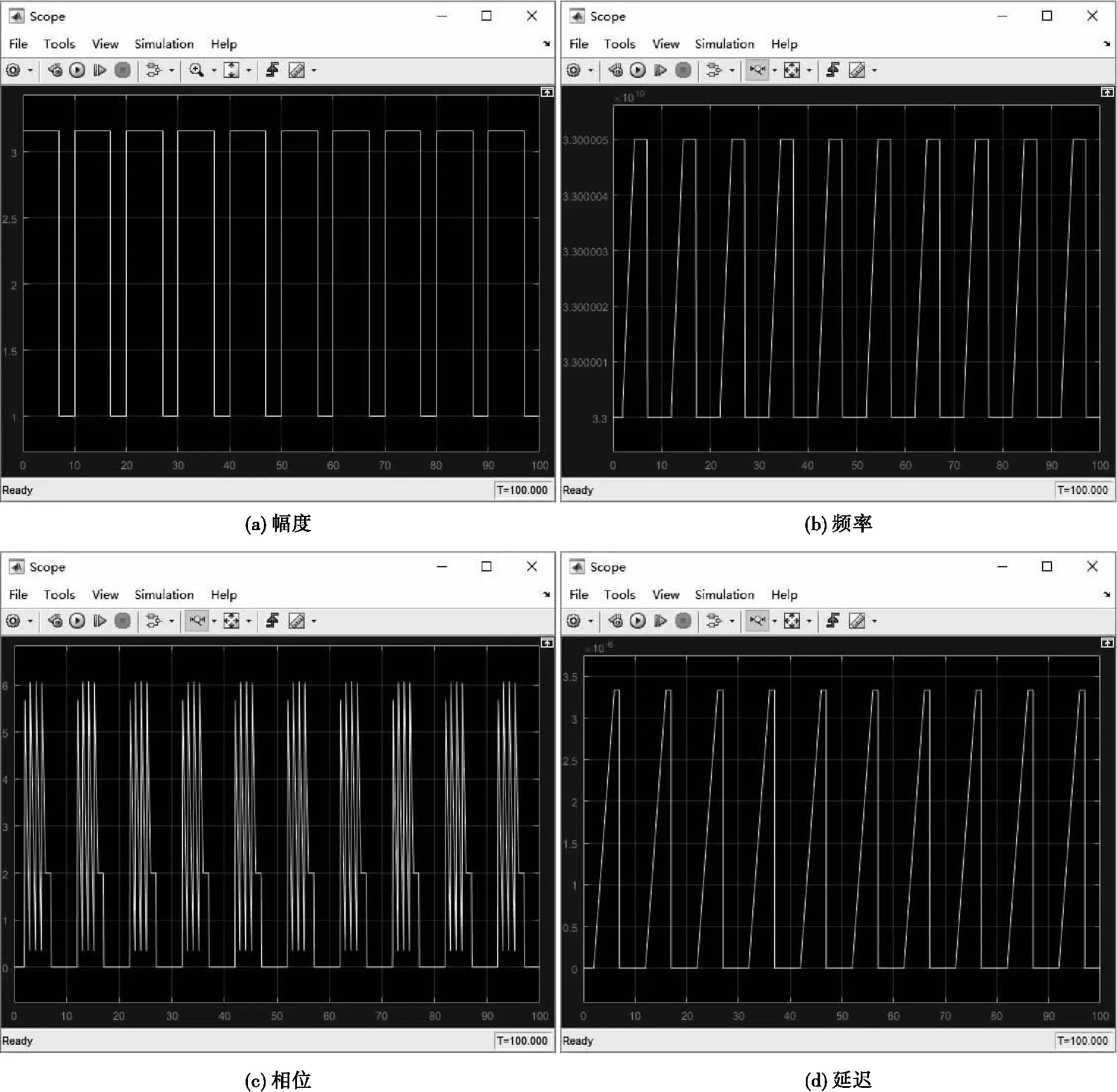
图6 距离和速度门联合拖引干扰参数仿真结果

由表3知，密集假目标干扰产生多个假目标，且每个假目标干扰波形的幅度、频率、相位和时延按一定规律产生，仿真中可以设功率、距离和多普勒在一定范围内变化，每一个假目标的功率、距离和多普勒在相应的变化范围内随机选择，另一方面，假目标数也可根据设置自动生成多个功能模块，图7显示了密集假目标干扰的实现框图和功率、距离、多普勒及相位参数的选择方法，图8显示了假目标为2和8时的程序实现框图。

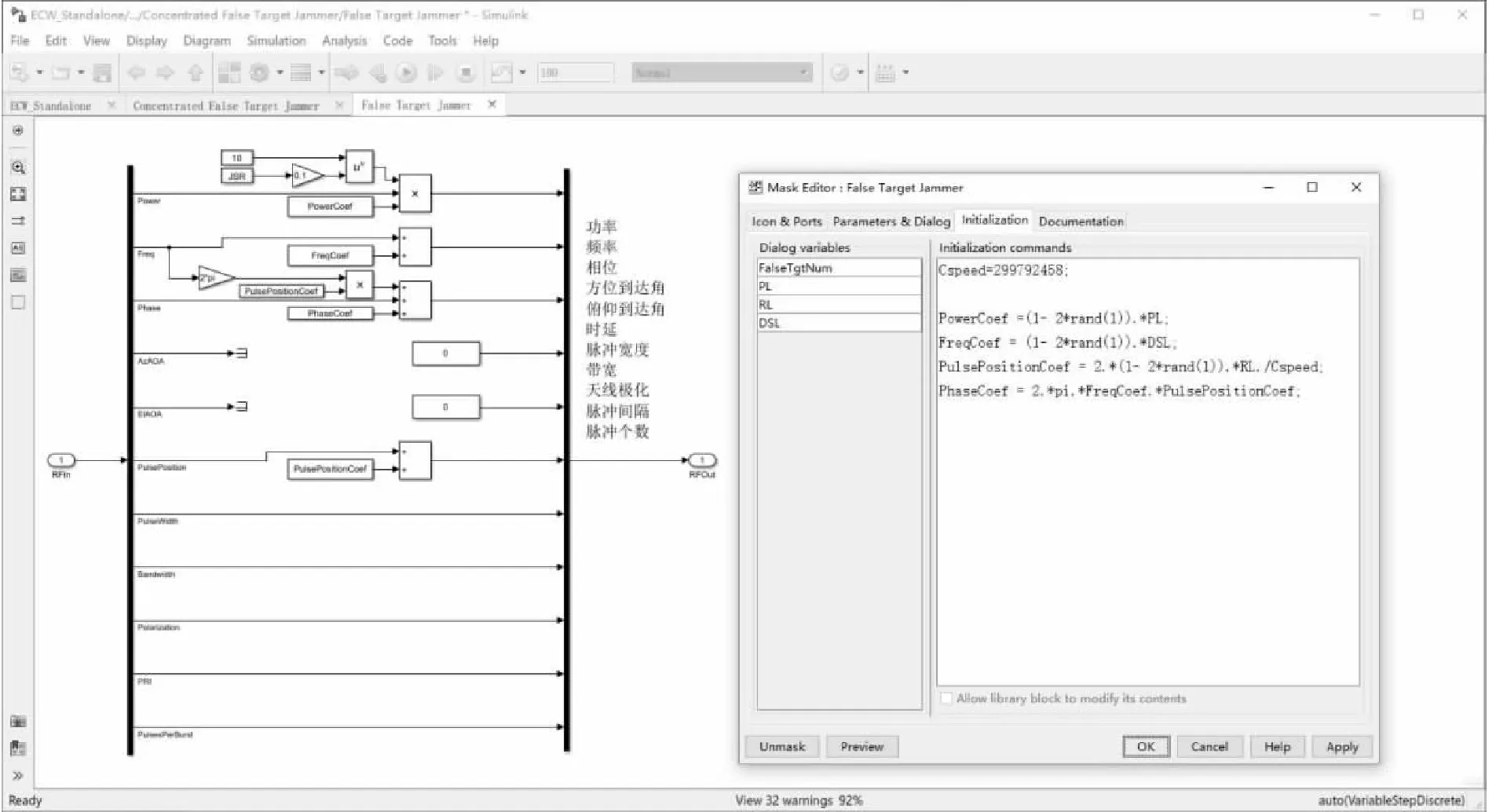
图7 密集假目标干扰的实现方法

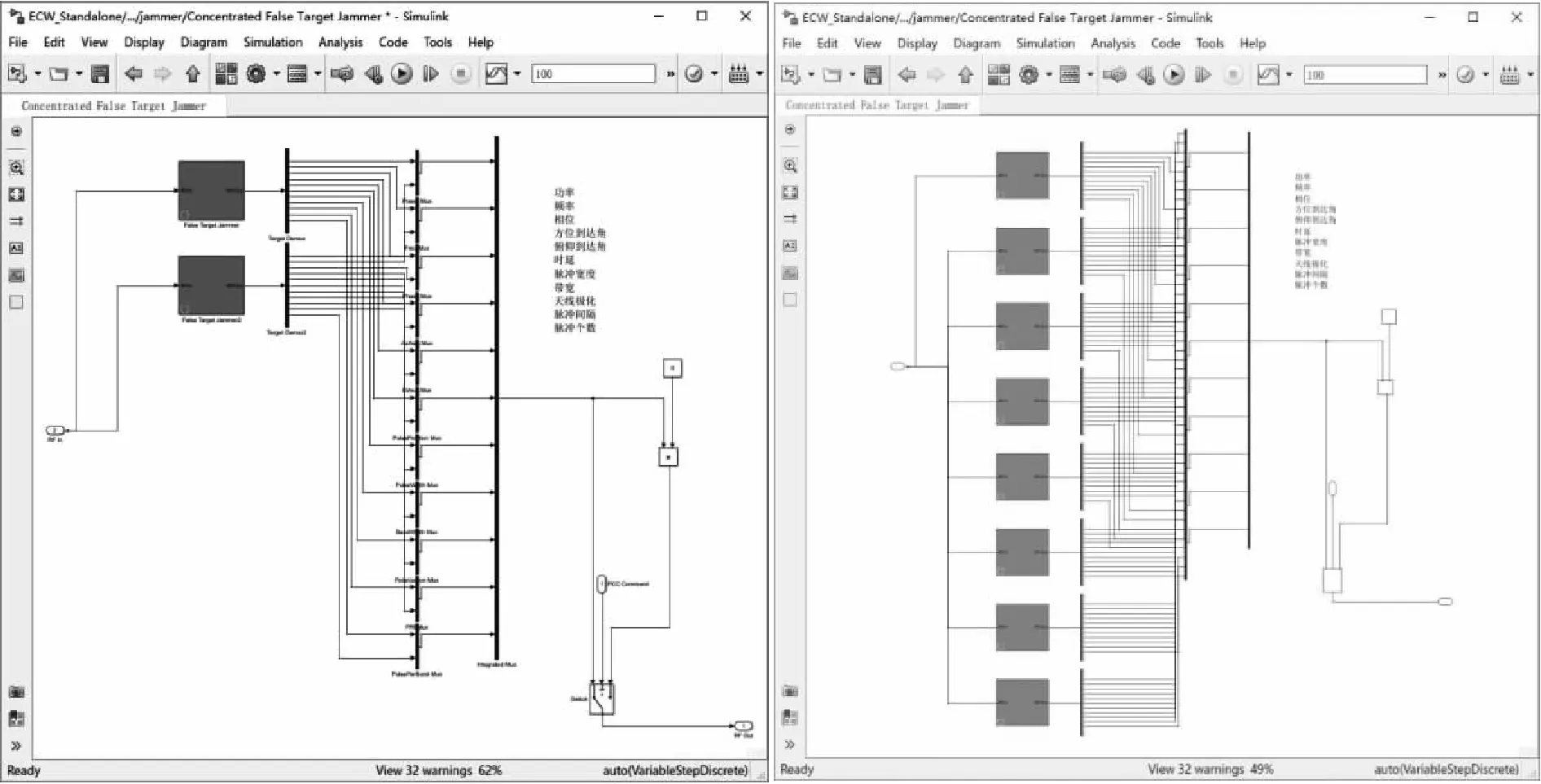
图8 密集假目标干扰数为2和8的实现方法

4 结束语

针对雷达数字化设计与仿真系统，从电子干扰仿真功能入手，基于统一的雷达波形的参数化接口给出了覆盖类和欺骗类电子干扰信号的参数描述，针对直达路径和单跳多路径说明了电子干扰波形参数的空间传播变化，并给出了电子干扰信号相对雷达的到达角计算方法。本文较为系统地阐述了数字化系统中雷达电子干扰生成的理论原理和计算方法，为雷达数字化设计与仿真系统电子干扰乃至电子战模拟提供了理论参考和方法依据，可借鉴于雷达电子干扰的设计与实现工作，并能结合雷达具体的信号波形及处理参数应用于对电子干扰效能的评估。