基于松弛半定规划零速滤波器的杂波图检测方法

剡熠琛 徐保庆 赵永波 李 易 高 剑 李雅梅

(1. 西安电子工程研究所 西安 710100；2. 西安电子科技大学 西安 710071)

0 引言

现代雷达工作环境十分复杂，杂波抑制是雷达信号处理的一个重要环节，雷达系统中最常用的杂波抑制方法都是利用目标与杂波在频谱上的区别对其进行区分，如动目标检测(Moving Target Detection，MTD)、动目标显示(Moving Target Indication，MTI)技术。但是，对于速度很低的目标而言，其频谱与地杂波通常混叠在一起，因此传统的杂波抑制手段会失效。为了提升雷达对低速目标的检测能力，就需要采用杂波图[1-5]检测方法。

杂波图检测的基本原理是：首先通过多帧扫描建立起杂波图，然后进行新一帧扫描，将回波数据经过一个零速滤波器来分离出杂波和低多普勒的目标回波[4]，然后将零速滤波器的输出通过杂波图的门限检测器，得到当前帧的检测结果，最后更新杂波图并进行下一帧的扫描与检测，反复迭代直至得到最终的检测结果。其检测原理图如图1所示。

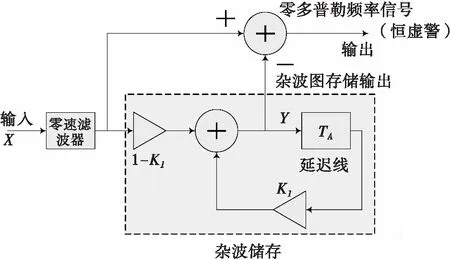
图1 零速滤波器检测原理图

零速滤波器与MTI滤波器的处理目的正好相反，零速滤波器是一个低通滤波器，其频率响应在零频(地杂波中心频率)附近为通带，其余频段为阻带，其输出只包括地面静止杂波以及超低速运动的目标回波。

传统的零速滤波器是采用零通道FFT滤波器来实现的，工程实现也比较简单。这种方法的缺陷在于，滤波器主瓣宽度是固定的，不能与地杂波谱宽相匹配，因此不能从回波信号中完整地将地杂波分离出来，当杂波谱较宽时，会使能0、±1多普勒通道作为零速滤波器，增加了系统复杂性，而且相邻FFT滤波器之间存在交叠损失，会影响杂波图的建立与超低速目标的检测性能。

针对上述问题，本文提出一种基于松弛半定规划零速滤波器的杂波图检测方法，该优化方法中将零速滤波器的设计转化成松弛半定规划模型，通过CVX工具箱[6]对该问题进行求解，优化出一个通带宽度与杂波谱宽相匹配，并且通带平缓的零速滤波器，只需一个多普勒滤波器就可以将杂波完整地分离出来。用该通道的输出建立并更新杂波图，可以提升雷达超低速检测性能，并降低了系统复杂性，具有实际工程意义。

1 信号模型

在脉冲多普勒雷达中，一个相干处理间隔(Coherent Processing Interval，CPI)内有N个脉冲，对应同一个距离单元的N个慢时间采样点表示为向量z，有z=[z1,z2,…,zN]T。根据参考文献[7]，该慢时间信号模型可以表示为

z=αa(v)+n

(1)

其中，a(v)=[a1,a2,…,aN]T是导频矢量，[·]T表示转置，ai=exp(j2π(i-1)v)，i=1,…,N。v=fdT，其中fd是目标的多普勒频率，T是脉冲重复周期。α∈包含目标反射、潜在跨越损失以及信道传播影响等因素。n=[n1,n2,…,nN]T包含杂波、干扰以及噪声分量，具有零均值、圆对称的统计特性。对于非自适应的多普勒滤波器来讲，滤波器的系数是提前设置好不变的，因此我们只要保证滤波器满足我们的要求，而在设计的过程中不必考虑目标信号的影响。

2 零通道FFT滤波器实现零速滤波器

实际工程应用中为了实现简单，通常使用级联FFT滤波器组中的第0号滤波器来实现零速滤波器的功能，其结构表示如图2所示。

图2 FFT滤波器结构示意图

FFT滤波器的权系数计算公式为

(2)

其中，n,m=0,1,2,...,N-1，n为脉冲编号，m为滤波器编号，N为雷达脉冲个数。FFT滤波器具有较高副瓣，导致副瓣大目标影响主瓣小目标的检测，通常会采用加窗的方法来抑制副瓣电平，但是加窗又会导致主瓣“变胖”，增益降低。当N=16时，零通道FFT滤波器的频率响应如图3所示。

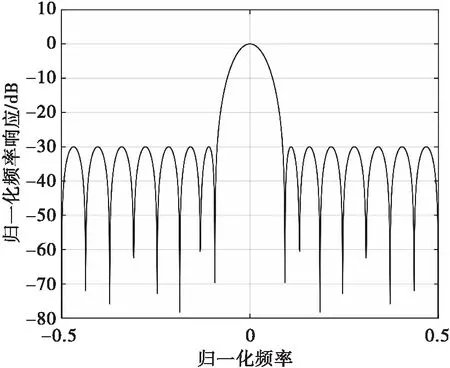
图3 零通道FFT滤波器频率响应

当雷达脉冲个数固定时，FFT滤波器主瓣宽度是固定的，如果地杂波谱宽较宽时，杂波会泄露到除零之外的其他多普勒通道中，影响其他通道目标的检测。此时，为了提升系统检测性能，就需要将±1多普勒通道、甚至±2多普勒通道也作为零速多普勒滤波器，参与到杂波图的积累与检测中来。假设雷达脉冲重复频率(Pulse Repetition Frequency，PRF)为1000 Hz，当地杂波谱宽为-100 Hz～100 Hz时，杂波图零速滤波器频率响应如图4所示。

图4 杂波图零速滤波器频率响应

该方法通过改变FFT滤波器的个数来使零速滤波器的通带宽度尽量与杂波谱宽度匹配，一方面提升了系统的复杂性；另一方面，当多个FFT滤波器作为零速滤波器时，相邻FFT滤波器响应之间存在交叠损失，会影响杂波图的建立与超低速目标的检测性能。

3 基于松弛半定规划的杂波图零速滤波器设计方法

通过上一小节的分析论述可以知道，传统FFT方法设计的零速滤波器，主要存在以下三个缺陷：

1)零速滤波器主瓣宽度不能根据地物杂波谱宽进行灵活设置，通过增加FFT滤波器个数来保证将杂波全部滤除，提升了系统的复杂度。

2)相邻FFT滤波器通带响应不够平坦，存在交叠损失，影响杂波图建立与超低速目标检测。

3)副瓣抑制能力有限，通过加窗方法会导致主瓣“变胖”，且增益降低，带来一定的信噪比损失。

针对上述问题，本节中通过利用松弛半定规划方法设计零速滤波器，其主瓣宽度在自由度满足的情况下可以灵活设置；其次，通过添加约束条件求解优化问题，可以使得零速滤波器的通带响应非常平缓，降低交叠损失，而且可以在主瓣宽度不变的情况下，降低副瓣。

3.1 松弛半定规划零速滤波器设计原理

松弛半定规划是凸优化问题的一个子类，利用松弛半定规划方法设计零速滤波器时，通过对滤波器输出的信干噪比以及在一系列旁瓣约束进行优化，采用谱分解理论以及对偶理论对优化问题进行转换，得到松弛半定规划模型，最终利用CVX工具箱求解出零速滤波器权系数。

首先，我们可以将该优化问题表示为

(3)

其中，R=Ri+Rn，为干扰加噪声协方差矩阵，Θ1和Θ2分别表示主瓣和旁瓣区域，式(3)中的约束条件即我们要求旁瓣电平的最大值要小于主瓣电平最小值的ξ倍。

进一步，我们对问题(3)进行转换得到公式(4)，β决定着主瓣的波动范围。

(4)

我们的目的是得到一个凸优化问题，但是在式(4)中，|wHa(f)|2≥1是非凸的，因而式(4)是非凸的，不能利用凸优化的方法找到问题的最优解。

对此，我们引出一个新的变量W=wwH，其中wHRw=tr{wHRw}=tr{RW}，Rs(v)=a(v)a(v)H。

(5)

这样，从|wHa(f)|2≥1到tr{Rs(v)W}≥1，问题就变成一个线性约束问题，但引入的rank(W)=1仍然是非凸的。对此，一般情况下，我们先丢弃这个约束，那么原问题就变成一个松弛的半定规划问题。

(6)

得到该松弛半定规划模型后，采用Matlab中的CVX工具箱对其进行求解即可得到W，然后经过谱分解方法就可以得到优化后的零速多普勒滤波器权值w，利用该权值设计零速滤波器，并进行后续的杂波图检测即可。

3.2 仿真分析

假设雷达脉冲个数N=16，脉冲重复频率PRF=1000 Hz，地杂波覆盖频段范围是[-100 Hz，100 Hz]，主瓣波动电平β=0.5 dB，副瓣相对于主瓣衰减电平为ξ=-30 dB，噪声功率为0 dB。

利用本文松弛半定规划方法设计的零速滤波器频率响应与传统FFT零速滤波器响应对比图如图5所示。由仿真结果可见，基于松弛半定规划理论的零速滤波器频率响应的主瓣宽度可以调整，可以自由设置使其对准我们感兴趣的频率区域，且主瓣区域响应平坦，FFT只能通过增加或减少滤波器个数来尽量与杂波谱匹配，存在交叠损失。由图6可见，FFT相邻滤波器之间有大约2.5 dB的交叠损失，基于松弛半定规划理论的零速滤波器的交叠损失大约0.36 dB，明显优于传统FFT滤波器。

3.3 零速滤波器设计方法对信噪比的影响分析

由图5、图6可见，基于松弛半定规划的零速滤波器主瓣会有展宽。因此会存在一定的信噪比损失，下面对该滤波器对目标信噪比带来的影响进行评估。

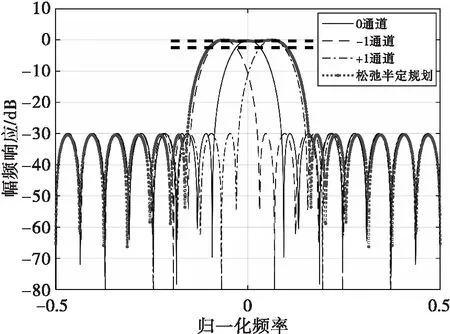
图5 松弛半定规划零速滤波器频率响应(最大值归一后)

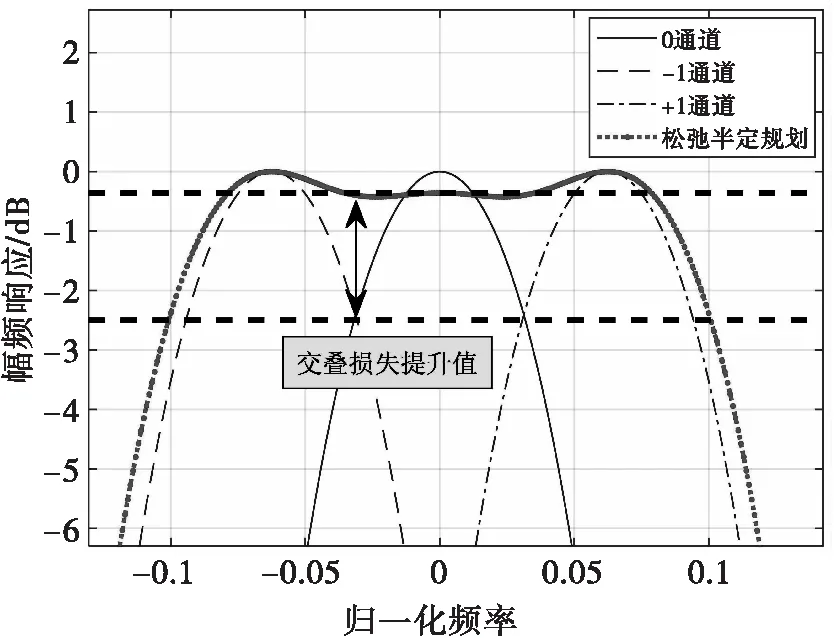
图6 松弛半定规划零速滤波器频率响应局部放大图(最大值归一后)

首先，对FFT滤波器及松弛半定规划滤波器的权值进行范数归一，归一化后的两组滤波器对高斯白噪声的增益均为1，图7为权系数范数归一后的零通道FFT滤波器与松弛半定规划零速滤波器的频率响应对比图。

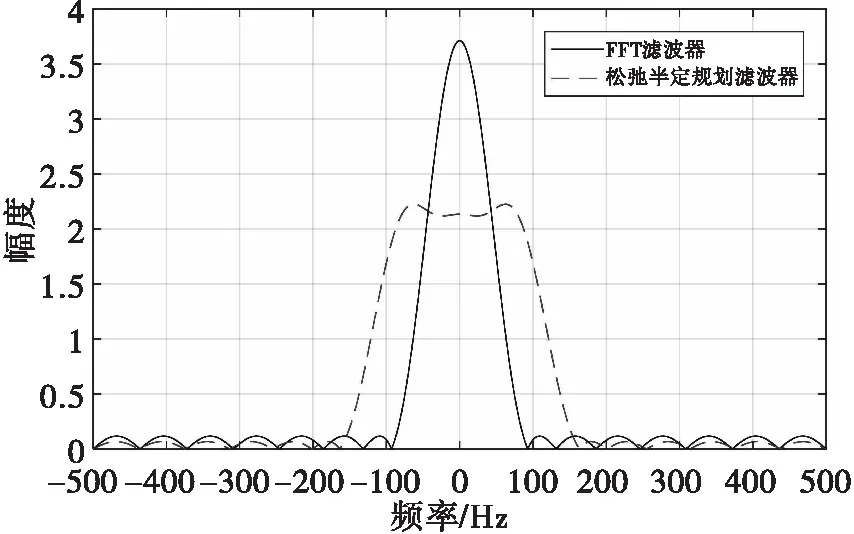
图7 零速滤波器响应对比图(范数归一后)

零速滤波器是应用于地杂波区域的，噪声强度远远小于地杂波强度，因此信噪比对检测性能的影响远小于信杂比。换而言之，杂波区的信杂比才是目标检测性能的决定因素，从图6交叠损失提升情况来看，本文提出的方法能够提升信杂比，对杂波区的慢速目标检测依然是有利的。

4 基于松弛半定规划零速滤波器的杂波图检测方法

4.1 杂波图检测步骤

基于松弛半定规划零速滤波器的杂波图检测方法具体步骤如下：

步骤1：雷达开机，在作用空域范围内进行M圈扫描，录取M圈杂波数据Xm，其中，m=0,1,...,M，通常取M≥10；

步骤2：根据录取的M圈杂波数据估计雷达阵地的杂波功率谱；

步骤3：根据这步骤2中估计得到的杂波谱宽度，确定所需杂波图零速滤波器的主瓣范围；

步骤4：根据前述松弛半定规划零速滤波器设计方法优化得到零速滤波器权系数；

步骤5：利用步骤1中录取得到的M圈杂波数据Xm与步骤4中优化得到的零速滤波器建立起杂波图；

步骤6：雷达开始第M+1圈的扫描，获得个方位的回波数据XM+1；

步骤7：将步骤6得到回波数据通过零速滤波器，并与杂波图进行相减得到剩余杂波，进行杂波图检测；

步骤8：确定杂波图更新系数，并对杂波图进行更新；

步骤9：令M+1，然后继续从步骤6开始执行，得到最终的检测结果。

4.2 计算机仿真

为了验证文中方法的有效性，作如下仿真实验。对两种零速滤波器下的目标检测性能曲线进行仿真分析。

1)实验一：

仿真条件：假设雷达在每个方位上的驻留脉冲数N=16，距离单元数r=512，雷达脉冲重复频率PRF=1000 Hz，建立杂波图的积累圈数为M=10，在距离单元r=70处加入目标，目标多普勒频率fd=31 Hz，信杂噪比SCNR=-30 dB。

仿真内容及结果：对回波信号进行仿真，并分别采用传统FFT零速滤波器与本文基于松弛半定规划零速滤波器进行处理并完成杂波图检测。回波信号的距离多普勒二维结果如图8所示，传统FFT零速滤波器的杂波图检测结果如图9所示，基于松弛半定规划零速滤波器的杂波图检测结果如图10所示。

图8 回波信号的距离-多普勒二维结果

由图9和图10可见，传统FFT零速滤波器的输出进行杂波图检测时，目标信号未过门限，无法检测到目标。基于松弛半定规划的杂波图检测方法中，信号值超过检测门限，可以检测到目标。

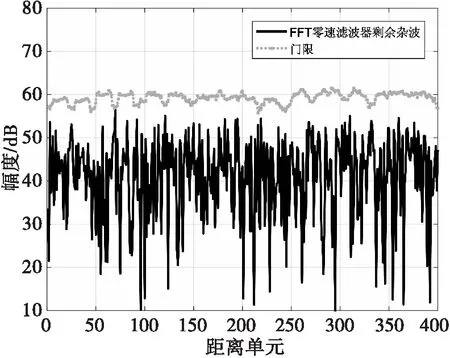
图9 传统FFT零速滤波器杂波图检测结果

2)实验二：

仿真条件：假设目标信杂噪比SCNR取值范围为-45 dB～-20 dB，步进间隔为1 dB，MonteCarlo实验次数为5000，其余条件同实验一。

仿真内容及结果：对目标检测性能进行仿真，基于传统FFT零速滤波器的杂波图检测性能曲线与基于松弛半定规划零速滤波器的杂波图检测性能曲线对比图如图11所示。

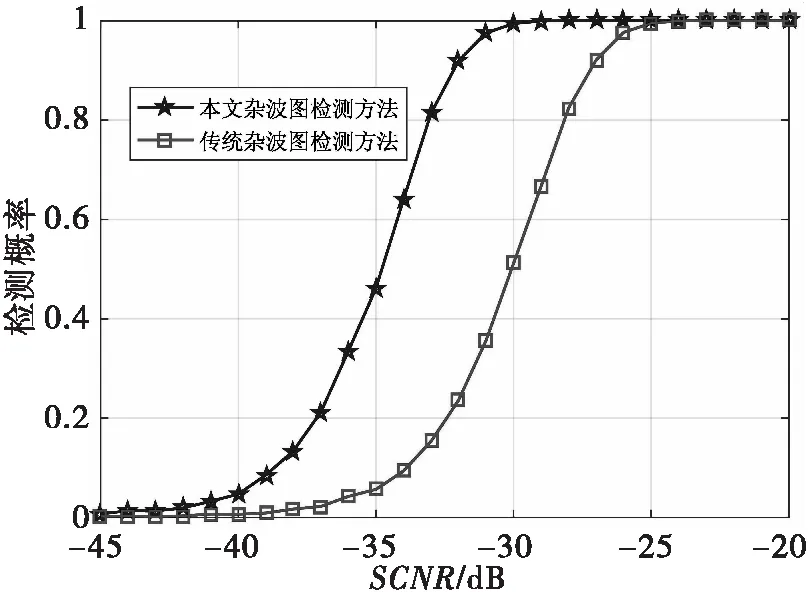
图11 检测性能曲线对比

由图11结果可见，本文基于松弛半定规划零速滤波器的杂波图检测方法的检测性能明显优于传统基于FFT零速滤波器的杂波图检测方法，可以有效提升杂波区的低速目标检测性能。

5 结束语

针对传统杂波图零速滤波器设计方法的缺陷，本文提出了一种基于松弛半定规划理论的杂波图零速滤波器设计方法。该方法可以根据杂波谱覆盖频段灵活设计主瓣宽度，不管杂波谱窄或宽，只需要一组多普勒滤波器就可以与杂波谱匹配，设计简单方便，同时可以降低系统的复杂性。此外，松弛半定规划零速滤波器主瓣宽度比较平缓，只有轻微波动，可以避免由于FFT相邻滤波器带来的交叠损失，有利于杂波图建立与超低速目标的检测性能。仿真结果表明，此方法具有一定的优越性，对杂波图零速滤波器的设计有一定的指导意义。