电沉积通孔铜箔数值模拟与实验研究

费翔昱，宫本奎,*，董志超, ，冯锐，孙玉梅，聂继伟

（1.山东理工大学材料科学与工程学院，山东 淄博 255049；2.北京理工大学先进结构技术研究院，北京 100081）

锂离子电池在储能方面潜力巨大，在交通、电子、通信等领域应用广泛。近年来，随着新能源汽车、便携式电子设备的发展，人们对锂离子电池性能提出了更高的要求[1]。集流体作为锂离子电池的重要组成部分，起着承载活性物质和汇集输出电流的作用[2]，其中负极集流体多使用铜箔。与压延铜箔相比，电解铜箔不仅能够满足能量密度、倍率性能等要求，而且生产成本更低[3]，因而被大量使用。为提高锂离子电池的能量密度、倍率性能，降低锂电池内阻，减少铜箔粉化，提高箔材的表面粘附力[1,4]，一些学者对集流体材料在厚度和结构方面开展了广泛而深入的研究[1-2]。目前，集流体材料厚度呈减薄趋势，期望减小集流体占比[5]；结构方面以多孔材料为主，有泡沫金属[6]、光子晶体[7]等，加工工艺较为复杂。

通孔铜箔作为多孔材料的一种，目前的制备方法有机械冲孔[8]、蚀刻[9-10]、激光加工[1,11]等，这些都是在已制造的铜箔基础上进行二次加工。与其他多孔材料相比，通孔铜箔的加工工艺较为简单，但制造成本与无孔铜箔相比明显增加。采用电沉积法一次成型制备通孔铜箔操作简单，得到的铜箔具有一般微孔铜箔的特点，且制造成本较二次加工方式显著降低，但存在厚度不均匀、表面粉化等问题。本文采用有限元方法，以Comsol Multiphysics软件模拟了通孔铜箔的电沉积过程，研究了通孔铜箔厚度分布和镀液中铜离子浓度变化。设计二维模型，研究了搅拌对电极反应过程中离子浓度分布及沉积层表面状态的影响；设计三维模型，研究了当镀液离子均匀分布时，通孔布局对厚度的影响。通过实验验证分析了模拟结果的可靠性，为设计优化通孔铜箔沉积工艺提供了技术支撑。

1 模型的建立

1.1 物理模型

采用石墨阳极板和TA1钛阴极板，尺寸均为10 mm × 10 mm × 2 mm，极间距在无特别说明的情况下为10 mm。除阴极板与阳极板正对表面，即微孔区域所在表面外，其他部位一律进行绝缘处理。电沉积槽底面直径58 mm，高度50 mm，入口直径7 mm、长15 mm，出口直径7 mm、长10 mm，建立的电沉积物理模型如图1所示。对铜箔激光加工直径100 μm的微孔，微孔中心距离200 μm，孔内进行绝缘处理，如图2所示，分别得到微孔呈矩形阵列和环形阵列均匀分布的阴极板A和阴极板B。

图1 电沉积通孔铜箔的二维模型(a)和三维模型(b)示意图Figure 1 Sketches of 2D (a) and 3D (b) models for electroplating copper foil with thorough holes

图2 阴极板A(a)和阴极板(b)的微孔分布Figure 2 Microhole distributions of cathode plate A (a) and cathode plate B (b)

1.2 数学表征

在电沉积通孔铜箔过程中，沉积层厚度δ按式(1)计算[12]。

式中MCu为铜的原子质量(63.546 g/mol)，ρCu为铜密度(8.92 g/cm3)，t为电沉积时间(单位：s)，F为法拉第常数(96 485 C/mol)。

局部电流密度jloc由Butler-Volmer公式(式2)计算[13]。

式中j0为交换电流密度，ci为离子i的浓度(单位：mol/L)，ci,0为初始离子浓度，αa和αc分别为阳极传递系数和阴极传递系数，η为过电位(单位：V)，R为理想气体常数[8.314 J/(mol·K)]，T为溶液的开氏温度(单位：K)。

在反应过程中存在离子对流、电迁移和扩散，离子浓度ci由电中性条件和物质传递过程质量守恒方程[12]计算，满足式(3)。

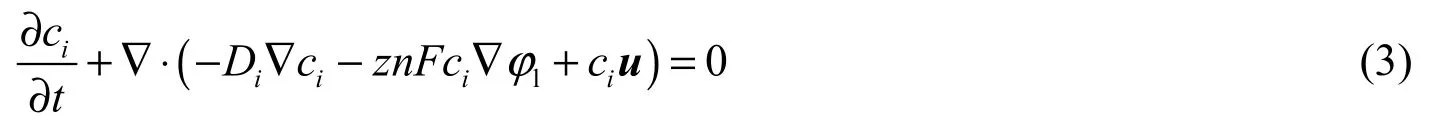
式中Di为离子i的扩散系数，z为离子i的电荷数，n为离子i的电子迁移数，φ1为电势(单位：V)，u为流速(单位：m/s)，∇表示梯度，∇⋅表示散度。

速度场u由Navier-Stokes方程[见式(4)]计算[14]。

式中ρ为溶液密度(单位：kg/m3)，g为重力加速度(9.8 m/s2)，μ为溶液的动力黏度(单位：Pa·s)，l为混合长度(单位：m)。

采用水平集方法[12]表征阴极表面铜沉积层的厚度分布，观察横截面的沉积形态，则式(1)变为式(5)。

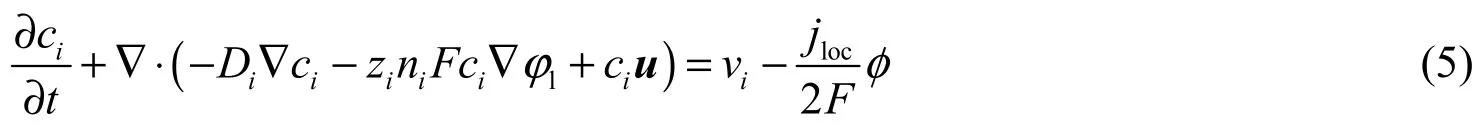
其中φ为水平集函数，vi为离子i的反应速率，由式(6)[12]描述。

其中εl为电解质的体积分数，在水平集方法中有判断电解质区域和控制反应区域的作用。

为简化模型，对模拟电沉积铜过程作出如下假设：

(1) 镀液为不可压缩黏性流，反应过程温度不变；

(2) 加入的添加剂极少，忽略添加剂对黏度和密度的影响；

(3) 忽略阳极析氧对溶液的作用及双电层对电流密度分布的影响；

(5) 电极和镀液的物理性质为各向同性。

2 电沉积通孔铜箔的模拟方案

2.1 网格划分

如图3所示，采用COMSOL Multiphysics软件对电沉积区域建模并进行网格划分。二维模型的网格总数为8 540，使用自由三角形网格，网格单元使用预定义的常规大小，电极表面网格单元采用预定义的细化网格，并为电极表面及槽内表面添加边界层网格，确保传质计算。为保证水平集精度，在两电极之间的区域使用常规细化操作对网格进一步细化。三维模型的网格总数为277 600，阴极板微孔尺寸小，与电极和槽体尺寸差异大，为保证孔的圆度，微孔采用极细化网格单元大小，表面采用较细化网格单元以保证沉积精度，槽体部分网格需求低，使用常规网格单元。

图3 二维模型(a)和三维模型(b)的网格大小分布Figure 3 Mesh size distributions of 2D (a) and 3D (b) models

2.2 参数设置

硫酸根离子的扩散系数(D)采用Stoke-Einstein方程[见式(7)][15]计算，单位为cm2/s。

式中NA为阿伏伽德罗常数(6.02 × 1023mol−1)，a为离子半径(单位：cm)。

氢离子的扩散系数DH采用式(8)[16]计算。

电解液密度ρ和动力黏度μ采用式(9)−(11)[17]计算。

式中cH2SO4为铜离子浓度，cH2SO4为硫酸浓度，单位都为mol/L。

反应参数受镀液体系和成分配比的影响[18-20]。以Hg|HgSO4电极为参比电极，铂电极为辅助电极，金电极为工作电极(工作面积为1 cm2)，在上海辰华CHI660E电化学工作站上进行循环伏安测试，获得本体系镀液的铜离子扩散系数DCu(II)= 1.73 × 10−6cm2/s。

分别选用石墨电极和TA1钛电极作为工作电极，铂电极为辅助电极，Hg/HgSO4电极为参比电极，通过塔菲尔(Tafel)测试得到交换电流密度j0、传递系数αa和αc以及平衡电位φ0(见表1)。

表1 Tafel曲线模拟结果Table 1 Results fitted from Tafel plots

电沉积数值模拟参数取值如下：铜离子80 g/L，浓硫酸100 g/L，温度35 °C，极间距6、10或14 mm，电流密度30、35、40或45 A/dm2，流速0、0.3、0.4或0.5 m/s，电导率166 S/cm。

3 结果讨论

3.1 仿真结果分析

电沉积过程中，铜离子在阴极表面还原而浓度降低，调节镀液流速和电流密度，计算阴极板微孔边缘(即图2中阴极板上点3处)的铜离子浓度随电沉积时间的变化，结果见图4。镀液相对静止时，阴极孔边缘铜离子被快速消耗，随电流密度升高，铜离子浓度快速降低，当电流密度为45 A/dm2时，电沉积进行约1.7 s时点3处的铜离子已被耗尽，此时阴极表面反应受铜离子扩散控制，铜离子消耗快，不能及时得到补充，最终导致镀层粉化[21]。搅拌镀液能够使阴极附近铜离子及时得到补充，镀液浓度维持稳定；随流速提高，铜离子的补充加快。而电流密度提高也会加快铜离子的消耗。为提高铜离子的还原沉积速率，可加强镀液搅拌和提高电流密度。图2中曲线初始阶段的波动是电流密度的缓慢提升和镀液流动不稳定所致。

图5是在电流密度为45 A/dm2、镀液流速分别为0.3 m/s和0.5 m/s下电沉积45 s时，镀液中铜离子的浓度分布。区域2的铜离子浓度最高，区域3最低。原因是铜离子在阴极还原而被消耗，使附近铜离子浓度降低；阳极发生析氧反应，生成大量氢离子，铜离子的相对浓度降低。总体而言，铜离子浓度分布均匀，最大浓度差仅0.04 mol/L。由式(2)可知，在铜箔制备过程中加强搅拌时可忽略铜离子浓度对厚度均匀性的影响。因此，为简化模型，忽略了铜离子浓度变化的影响，研究在三维模型下孔分布对通孔铜箔厚度的影响，结果见图6。通孔铜箔的厚度为15 μm时，2种阴极板上点1和点2处电沉积铜箔厚度均相差较小。采用阴极板A的通孔分布方式时，沉积层较厚，点3处铜箔厚度的偏离程度高于阴极板B，原因是阴极板A各方向的孔间距不等。

图4 不同镀液流速下阴极孔边缘铜离子浓度随电沉积时间的变化Figure 4 Variation of copper ion concentration at the edge of hole in cathode with electrodeposition time at different flow rates of electrolyte

图5 在不同镀液流速下电沉积45 s后铜离子浓度的分布Figure 5 Distribution of copper ion concentration after electrodeposition at different flow rates of electrolyte for 45 s

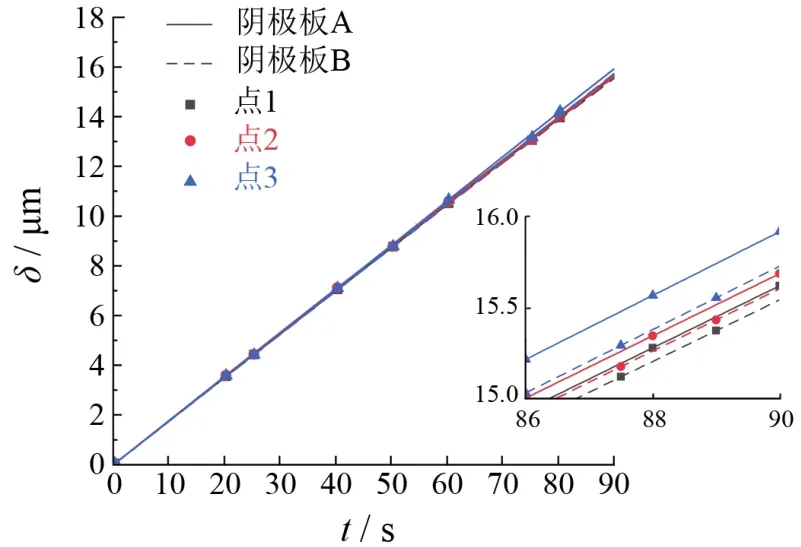
图6 阴极表面典型位置沉积层厚度随时间的变化Figure 6 Variation of thickness of coatings at typical positions of cathode with the electrodeposition time

在不同极间距下，数值分析图2b中的线ab(对应距离记为Dab)和线cd(对应距离记为Dcd)上通孔铜箔厚度的分布。如图7和图8所示，极间距固定时，随电流密度升高，通孔铜箔厚度逐渐增大；在相同电流密度下，随极间距增大，通孔铜箔厚度逐渐减小；线ab上的铜箔厚度大于线cd上的铜箔厚度。

图7 在不同极间距下图2b中线ab上铜箔的厚度分布Figure 7 Thickness distribution on line ab of copper foil noted in Figure 2b at different interelectrode spacings

图8 在不同极间距下图2b中线cd上铜箔厚度分布Figure 8 Thickness distribution on line cd of copper foil noted in Figure 2b at different interelectrode spacings

为了统计厚度分布偏差(δerror)，引入式(12)[22]。

式中δmax、δmin和δave分别是通孔铜箔厚度的最大值、最小值和平均值。

绘制电流密度对铜箔厚度偏差的影响，如图9所示。在相同电流密度下，随极间距增大，厚度偏差逐渐减小；相同极间距下，提高电流密度会增大厚度偏差。当电流密度为45 A/dm2时，随极间距从6 mm增至14 mm，厚度偏差从2.212 3%减小至0.928 8%；当极间距为14 mm时，随电流密度从30 A/dm2增至45 A/dm2，厚度偏差从0.928 8%增至1.276 2%。这说明电流密度和极间距都对铜箔厚度分布有影响，极间距的影响更为显著，而电流密度的影响较小。在高电流密度下电沉积时可通过增大极间距来保证沉积效率。

图9 极间距和电流密度对铜箔厚度偏差的影响Figure 9 Effect of interelectrode spacing and current density on thickness deviation of copper foil

3.2 电沉积实验验证

电沉积实验选用石墨电极作为阳极，40 mm × 40 mm的TA1纯钛作为阴极，钛板表面孔数约4万个，孔径为100 μm，呈矩形阵列分布，并作绝缘处理。根据模拟结果，在极间距14 mm、镀液流速0.5 m/s、电流密度45 A/dm2及其他参数与2.2节相同的条件下进行电沉积实验。从图10可知，电沉积90 s所得铜箔通孔分布均匀，孔边缘较光滑。

图10 电沉积90 s所得通孔铜箔的形貌Figure 10 Morphologies of through-hole copper foil obtained by electrodeposition for 90 s

从图11可知，电沉积时间对孔径的影响不明显，孔径不一主要是由于在进行形貌观察时截面的位置是随机截取的。取不同电镀时间下的铜箔厚度平均值绘制曲线并与模拟结果对比，结果见图12。铜箔厚度随电沉积时间延长而呈线性增长，样品厚度变化与模拟结果非常接近，两者之间存在的微小误差主要是由于在模拟过程中忽略了添加剂、电极各向异性、电极表面状态等因素。

图11 电沉积不同时间所得通孔铜箔的截面形貌Figure 11 Cross-sectional morphologies of through-hole copper foils obtained by electrodeposition for different time

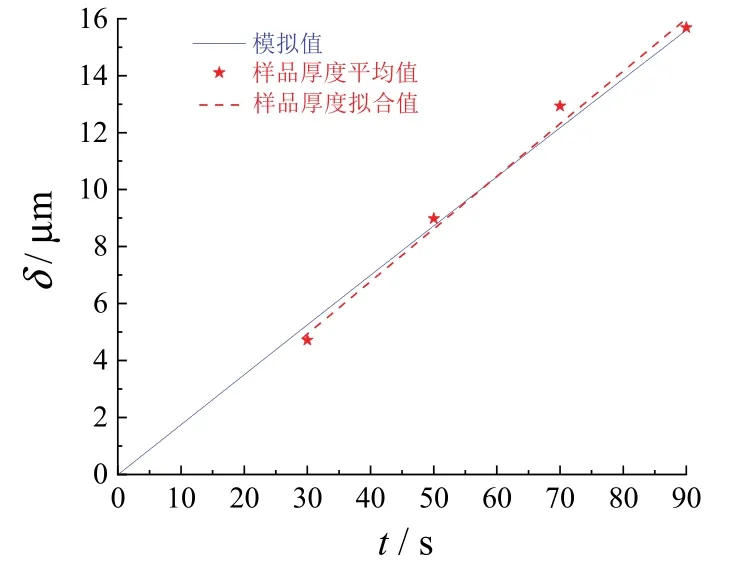
图12 孔间铜箔厚度模拟值与实验值Figure 12 Simulated and measured thicknesses of copper foil between holes

由图13可知，实际铜箔样品的厚度由孔间生长中心处向孔边缘处逐渐变薄，这与模拟结果呈现的孔边缘较厚不同，原因是模拟过程未考虑已沉积部分作为新表面继续沿孔的径向沉积铜，使孔径变小，形成较薄的边缘。图13a与图13d中的模拟形貌M较吻合，而图13c与图13d中的模拟形貌N较吻合。

图13 电沉积90 s时通孔铜箔横截面的实际形貌和模拟形貌Figure 13 Actual and simulated cross-sectional morphologies of through-hole copper foil obtained by electrodeposition for 90 s

4 结论

(1) 数值模拟可直观反映出电沉积过程中铜离子浓度分布，并预测通孔铜箔沉积厚度的变化趋势，对电沉积制备通孔铜箔工艺有指导作用。

(2) 静止状态下电沉积时，孔附近离子迅速消耗，引起铜箔粉化。搅拌能使铜离子分布均匀，有利于铜箔均匀沉积。提高镀液流速和减小电流密度能够使镀液的离子浓度保持稳定。

(3) 与矩形阵列孔分布方式相比，环形阵列孔分布方式可使通孔铜箔厚度更均匀。

(4) 极间距对通孔铜箔厚度均匀性的影响较大，提高极间距可使厚度偏差显著降低，提高电流密度则使厚度偏差增大，但影响较小。

(5) 电沉积实验结果与模拟结果较吻合，所得通孔铜箔厚度较均匀。