液固流化床内双组分颗粒流动数值模拟

贾雨彬 王树青 朱玉颖

（1.东北石油大学石油工程学院；2.大庆油田有限责任公司采油四厂）

液固流化床反应器（LSFB）以其良好的搅拌、传热和传质性能，在化工、能源、冶金、材料、医药、食品及环保等领域得到了广泛应用。 在许多工业过程中，LSFB中的颗粒往往具有不同的尺寸和密度，这直接影响到颗粒的沉降速度和颗粒的分离、 混合等流动行为。 双组分液固流化床（BLSFB）的分离与混合有均匀混合、非均匀混合、不完全分离和完全分离4种模式［1］，但是其颗粒混合和分离受到流体速度、颗粒密度、颗粒形状和大小的影响［2～4］。

随着计算机技术的飞速发展，采用数值模拟方法对二元固液流化床的流动进行研究已成为学术主流。 近年来，许多学者综合利用计算流体动力学（CFD）连续相模型和离散元模型（DEM）对双组分颗粒流化床混合和分离进行了数值模拟研究。Seibert K D和Burns M A研究了液固流化床内不同大小与密度的颗粒的流动现象［5］。 采用统计力学方法捕获粒子的随机运动，并结合颗粒体积分数验证了液固流化床内双组分颗粒的弥散、分离和反混。 Renzo A D等利用DEM-CFD方法模拟再现了液固流化床层反演现象，研究了局部的粒子流场，显示出固体在不断形成和消失的混乱漩涡中的不规则运动是颗粒混合机制；在强烈不均匀浓度分布的情况下， 流体-颗粒相互作用力沿着床层高度呈现恒定的趋势［6］。

笔者采用MFIX-DEM方法对Galvin K P等的双组分液固流化床流动实验［7］进行数值模拟。 首先，对双组分颗粒在液固流化床内的运动特性进行分析， 得到颗粒分离与混合的基本运动规律；其次，对双组分颗粒在混合与分离过程的受力情况进行分析，得到颗粒实现混合和分离的基本机制；最后，引入颗粒拟温度对颗粒随机运动进行分析，得到颗粒随机运动的基本机制。

1 数学模型

1.1 连续相控制方程

连续性方程：

动量方程：

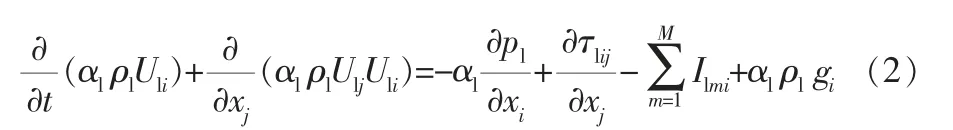
其中，t是时间；αl是液相体积分数；ρl是液相密度；Ul是控制方程中液相瞬时速度的系综平均；pl是热力学压力；τl是液相应力张量；M是固体颗粒相总相数；Il是液相与颗粒相的动量交换相；g是重力加速度；下角i，j仅限于爱因斯坦求和约定。

1.2 颗粒运动方程

单个颗粒在流化床中的运动可以通过牛顿第二定律进行描述：

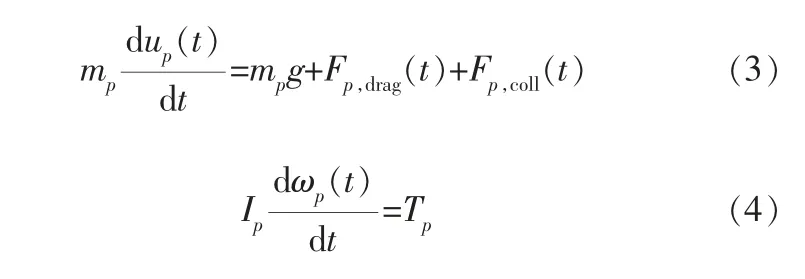
其中，mp、up、Ip、ωp、Tp分别为颗粒p的质量、速度、转动惯量、角速度、力矩；Fp，drag为颗粒运动过程中受到周围流体给的曳力（包含颗粒所受到周围流场的压力梯度力）；Fp，coll为颗粒的碰撞力（软球碰撞模型）［8］。 t时刻固相中的第m相中颗粒p在k-th网格内所受到的曳力为：

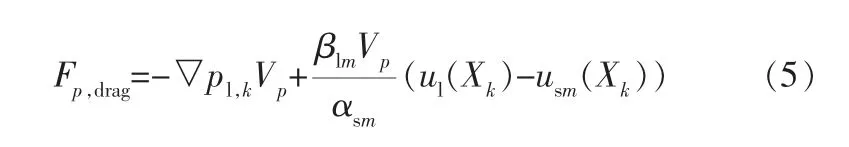
其中，▽pl，k是在k-th网格中心的压力梯度；Vp是颗粒p的体积；βlm是k-th网格内局部的曳力系数；αsm是固相中m-th相颗粒的体积分数；ul（Xk）是k-th网格内液相速度；usm（Xk）是网格内m-th相颗粒的局部平均速度。 这里的曳力系数采用适用于多组分的BVK曳力模型［9］，其表达式如下：

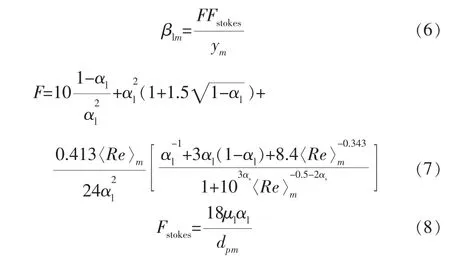
其中，F为无量纲力；Fstokes为stokes力；ym为mth相颗粒的体积分数；m为平均雷诺数；αs为固相体积分数；μl为液相动力粘度系数；dpm为m-th相颗粒的直径。

1.3 边界条件及模拟参数

笔者对Galvin K P等的液固流化床内双组分颗粒流动实验［7］进行数值模拟，并将实验装置简化成0.05m×1.2m的二维矩形。 初始条件下，颗粒在床层内均匀堆积，其中轻颗粒在下层，重颗粒在上层。 采用速度入口和压力出口边界条件，并且假设入口处液相速度均匀分布，液相在壁面处采用无滑移边界条件。 采用MFIX-DEM开源代码对BLSFB内的颗粒流动进行数值模拟， 其中在空间上采用二阶精度的superbee离散方法， 在时间上采用隐式Euler方法。模拟基本参数见表1。模拟的网格数为10×240，采用自适应时间步长，其范围是10-7～10-3，模拟时间为60s，如非特殊说明，取后10s的时均数据进行分析。

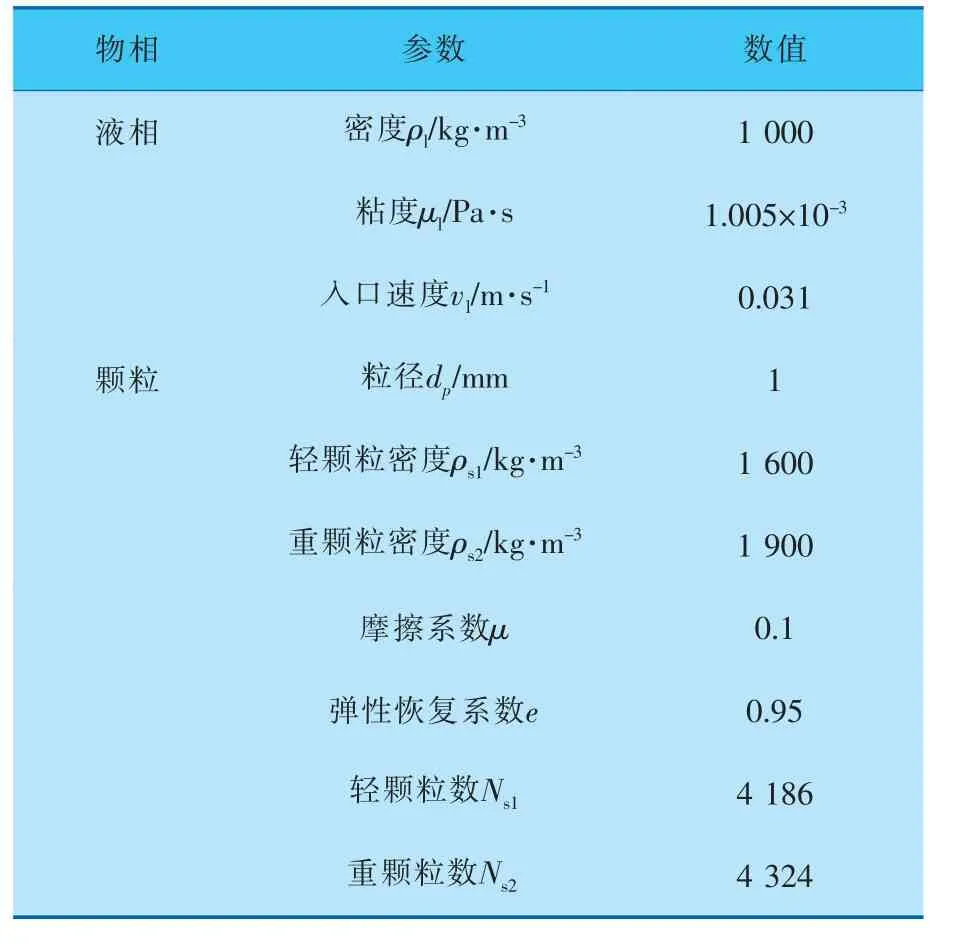
表1 模拟基本参数

2 计算结果

2.1 模型验证

入口速度0.031m/s时颗粒体积分数的轴向分布曲线与实验对比如图1所示。 由图1可知，轻、重颗粒体积分数的模拟曲线与实验数据吻合较好，验证了模拟的有效性。

2.2 颗粒运动基本特性

图2为入口速度0.031m/s时颗粒的瞬时运动图，其中红色圈代表轻颗粒，蓝色圈代表重颗粒。 由图2可知，颗粒的运动规律为：在初始时刻，轻颗粒均匀填充在底层，重颗粒填充在顶层；当入口有流体注入时，两种颗粒在流体的带动下一起向上运动，由于两种颗粒与流体的密度差不同，而且在壁面处流体速度很小对颗粒的携带能力较弱，使得轻颗粒在床层中心向上运动，重颗粒沿着壁面向下运动；颗粒之间的碰撞与接触使得两种颗粒进行混合；最终在颗粒与流体的密度差作用下使得两种颗粒发生分离。

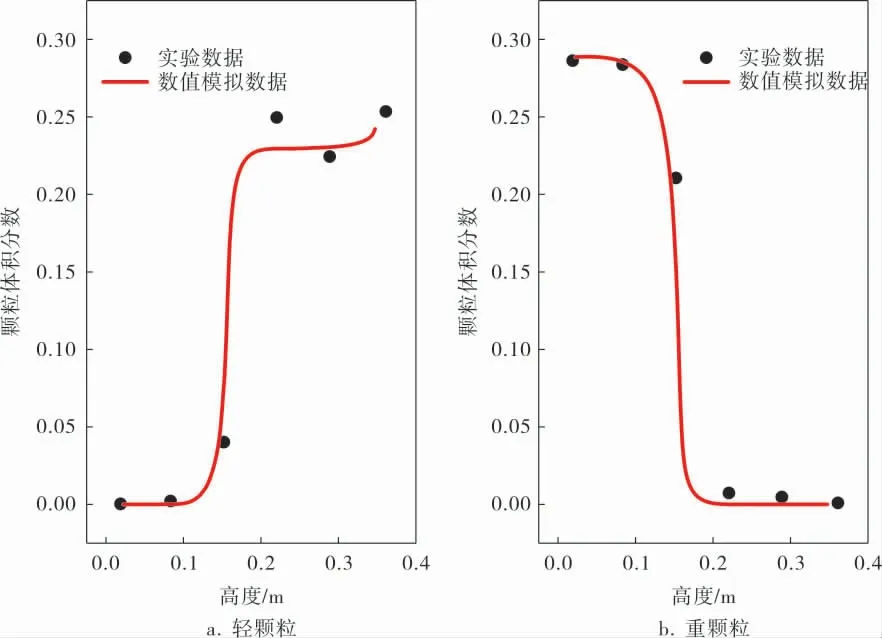
图1 轻、重颗粒体积分数的模拟曲线与实验数据

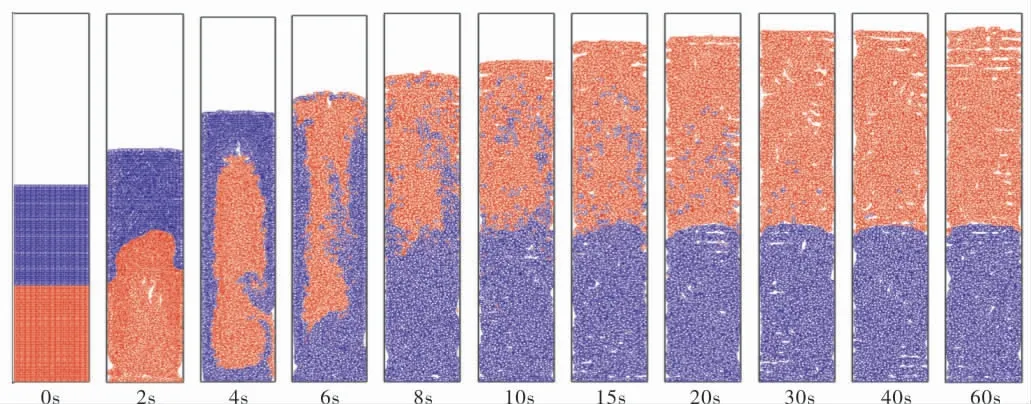
图2 入口速度0.031m/s时颗粒的瞬时运动图

2.3 颗粒受力分析

图3为入口速度0.031m/s时颗粒的受力分布时均图。 由图3可知，除了碰撞力外，与轴向力相比颗粒所受到的径向力更小，说明颗粒的轴向力对颗粒运动起主导作用。 通过颗粒碰撞力的分布可以发现， 不同方向上颗粒的碰撞力大小相仿，说明颗粒碰撞各向同性。 通过颗粒轴向力的分布可以发现，轻、重颗粒的曳力存在明显差距，说明轴向上轻、重颗粒曳力的差异对颗粒分离起主导作用。

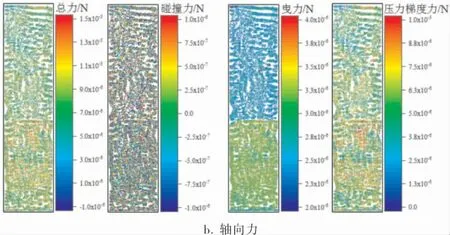
图3 入口速度0.031m/s时颗粒的受力分布时均图

图4是入口速度0.031m/s时颗粒所受到的轴向力随时间变化曲线。 由图4可知，当两种颗粒由初始的分离状态进入混合状态时，颗粒所受到的各种力均发生剧烈变化，说明当两种颗粒混合时颗粒之间以及颗粒与流体之间发生剧烈的作用。在混合状态时，碰撞力、曳力和压力梯度力的数值关系依次是压力梯度力大于颗粒间的碰撞力大于颗粒所受到的流体曳力，说明流体的紊乱运动带动颗粒的不规则运动从而引起颗粒之间的随机碰撞，此时颗粒的随机碰撞是颗粒在混合状态下的主要运动形式。 在颗粒分离时，通过力的平均值和标准差可以发现，与混合状态不同的是曳力大于颗粒间的碰撞力，并且轻、重颗粒所受到的曳力存在明显差异，验证了轻、重颗粒之间的曳力差异是造成两种颗粒分离的主要因素。 综合分离和混合过程可以发现，压力梯度力在总力中始终处于主导地位，说明流体的紊乱运动是颗粒随机运动的主要因素。

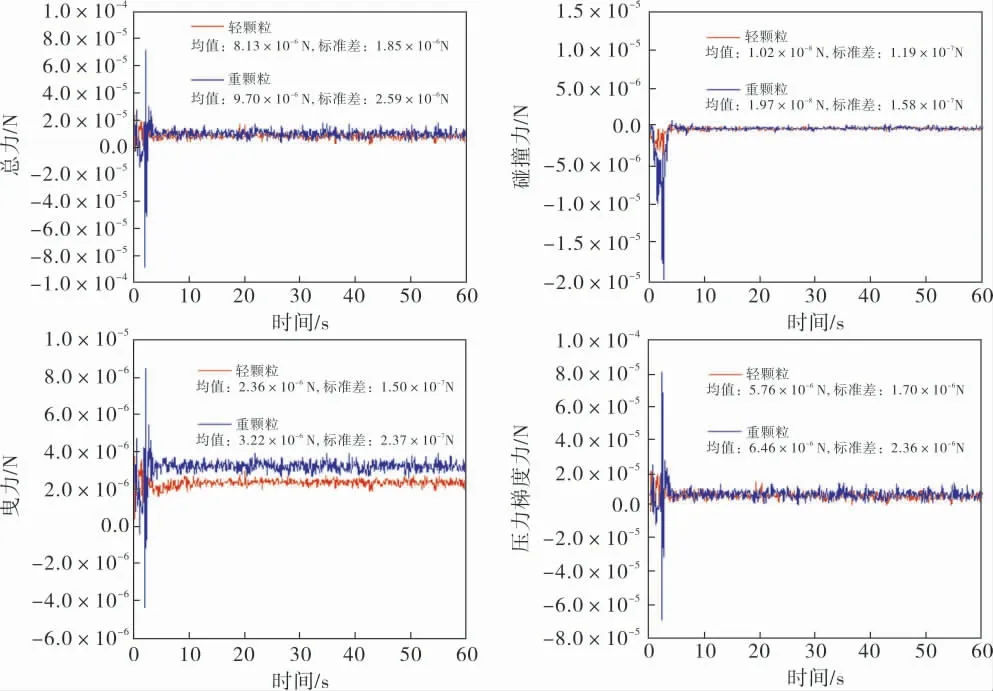
图4 入口速度0.031m/s时颗粒所受到的轴向力随时间变化曲线

2.4 颗粒拟温度

为了更好地分析局部区域内颗粒的随机脉动，笔者引入颗粒动理学中的颗粒拟温度对颗粒的随机脉动做定量分析。 其中颗粒拟温度θ的表达式如下［10］：

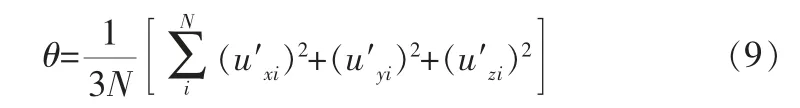
其中，N为计算网格内的颗粒数；u′i为计算网格内第i个颗粒的脉动速度。

图5为入口速度0.031m/s时颗粒拟温度的散点分布图。 由图5可知， 重颗粒的颗粒拟温度较大，两种颗粒的拟温度集中区域对应的颗粒体积分数与图1中的颗粒体积分数相当， 说明在此工况下颗粒拟温度主要受颗粒体积分数的制约。 由图1可知， 重颗粒的体积分数在床层的底层相比轻颗粒更大，此时颗粒的接触几率更大。 另外，由受力分析可知重颗粒受到的力更大，颗粒的随机运动更剧烈，所以重颗粒的颗粒拟温度更大。

图5 入口速度0.031m/s时颗粒拟温度的散点分布图

3 结束语

笔 者 采 用MFIX-DEM 方 法 对Galvin K P 等的双组分液固流化床流动实验进行数值模拟。模拟结果与实验数据吻合良好， 并得到如下结果：

a. 在床层内颗粒的分离与混合过程是在颗粒与流体的密度差带动下轻颗粒向上运动，重颗粒向下运动，最终两种颗粒实现分离。

b. 压力梯度力在颗粒的运动过程中占主导地位， 是颗粒随机运动的主要因素； 碰撞力在颗粒的混合过程中起主导作用； 轴向曳力在颗粒的分离过程中起主导作用。

c. 颗粒拟温度受颗粒的体积分数制约，与轻颗粒相比重颗粒的颗粒拟温度相对较大。