基于极限学习机的新型建筑材料力学性能预测方法

张勇

（青岛酒店管理职业技术学院 酒店工程学院，山东 青岛 266100）

如新型水泥基复合材料，高强、高性能混凝土材料，新型墙体材料，新型建筑隔热和吸声材料等都属于当前应用较为广泛并且关注度较高的新型建筑材料，如果能够妥善地对其进行应用不但可以达到最初的建筑目的，还可以在完成相关设计的同时满足其他的需求，因此如何能够良好的应用这些新型建筑材料是目前国内外较为关注的焦点之一[1]。据资料显示，投入应用的新型建筑材料普遍都是在满足最初的本质要求标准上增添了其他的些许功能，从而达到包容性更高、应用层次更广的目的[2]。而要达到这一目的，就要使建筑材料的自身结构发生改变，在这一过程中它的力学性能也会随之发生改变，经过国内外科学家与相关工作人员长时间的观察与总结发现，当前能否良好应用好新型建筑材料的主要要素就是能否精确的对新型建筑材料的力学性能进行预测[3]。目前国内外预测新型建筑材料力学性能的主要手段都是采用模拟环境抽样观察的方式来进行，就是在特定的环境下加快新型建筑材料的应用进程并在该过程中记录新型建筑材料的力学性能各项指标，以达到预测的目的。然而该手段不但资金要求过高且耗时长，而且得到的预测结果也可能并不具有普遍性，因此这仍是该领域的一大难题[4]。本文通过极限学习机设计了一种新的新型建筑材料力学性能预测方法，该方法可以应用极限学习机理念将新型建筑材料的各项力学性能因子化并相对应地进行提取分析，最终达到预测的目的，不但准确而且高效。

1 基于极限学习机的新型建筑材料力学性能因子提取

目前所需要预测的新型建筑材料的力学性能主要包括弹性极限、强度极限、断裂韧性、抗冲击性、疲劳度等，本文通过极限学习机的算法理念设计出来一种双隐层的前馈神经网络[5]。

本文设计的网络结构可以通过极限学习机的相关公式(1)来对它们整体的温度、湿度、密度以及材料混合比例进行相关的计算，通过相关的计算可以达到提取弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子的目的[6]。其中，T, W, M, K 分别为这类复合类建筑材料的整体的温度、湿度、密度以及材料混合比例，a, b, c, d, e分别为该双隐层的前馈神经网络通过公式计算所提取的弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子，它们构成了接下来需要进行分析的力学性能因子分析组A, B, C, D, E，但是各因子组中只有一个因子是最接近该类新型建筑材料力学性能的表达因子[7]。

而针对新型建筑隔热和吸声材料等这一类高度成型的新型建筑材料，本文设计的网络结构可以通过极限学习机的相关公式(2)来对它们的面积、组成成分、高度成型率进行计算，进而得到所提取的弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子[8]。

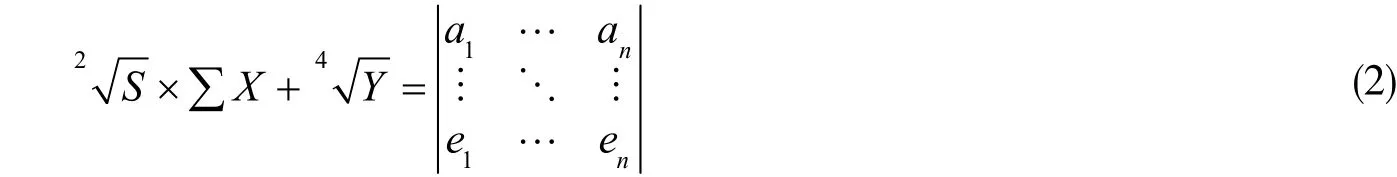
其中，S, X, Y 分别为这一类高度成型的新型建筑材料的面积、组成成分以及高度成型率，而由于新型建筑材料的力学性能本质相同，所以该双隐层的前馈神经网络通过公式计算所提取的弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子也可以用a, b, c, d, e 来表示，得到的力学性能因子分析组也为A, B, C, D, E[9]。

2 基于极限学习机的新型建筑材料力学性能因子分析与预测

当完成对新型建筑材料力学性能因子的提取后，本文会通过极限学习机理念创造的双隐层的前馈神经网络分别对所提取的弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子分别进行分析，从而得到各因子组中最为准确的最终表达因子[10]。

弹性极限因子所构成的因子组A 主要表示了相对应的新型建筑材料在受到外力一段时间后并去掉外力，该新型建筑材料能够恢复原状的最大外力极限，本文的预测算法创造的双隐层的前馈神经网络会对弹性极限因子组A 进行观察分析，最终因子组A 中波动性最强的因子ax则为我们最终分析得到的弹性极限表达因子[11]。

强度极限因子所构成的因子组B 主要表示了相对应的新型建筑材料产生损毁时受到的外力极限，继续采用上述方法对强度极限因子组B 进行观察分析时，其中稳定时间最长的因子bx即为分析得到的最终强度极限表达因子[12]。

断裂韧性因子所构成的因子组C主要表示了新型建筑材料在出现断裂纹后抵抗裂纹能力扩展的一种度量，本文在对断裂韧性因子组C 进行分析时需要通过公式(3)来进行计算，最终得到断裂韧性表达因子cx。

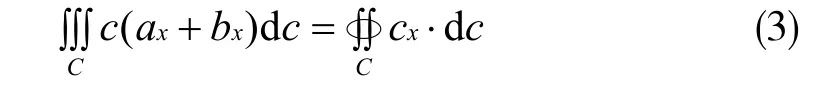
由于新型材料的断裂韧性与其弹性极限以及强度极限有着直接的关系，因此在分析断裂韧性表达因子cx时只有最符合上述关系式的c 才为最终得到断裂韧性表达因子cx。弹性极限表达因子、强度极限表达因子断裂韧性表达因子3 种因子的分析图如图1 所示。

抗冲击性因子所构成的因子组D主要表示了相对应的新型建筑材料抗冲击破坏的能力，仍然采用之前的方法冲击因子组D 中的所有因子，得到最终抗冲击性表达因子dx[13]。

疲劳因子组成的因子组E 主要表示了相对应的新型建筑材料永久性损伤逐渐增加直至完全被破坏的一个过程，设计算法创造的双隐层的前馈神经网络会对疲劳因子组E 分析时会通过公式(4)来进行计算，最终得到疲劳表达因子。

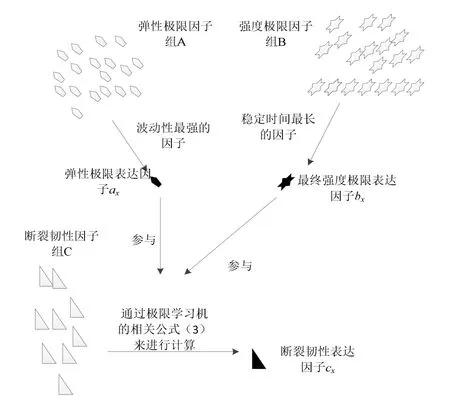
图1 3 种因子的具体分析图

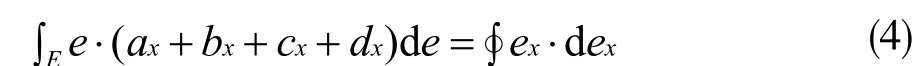
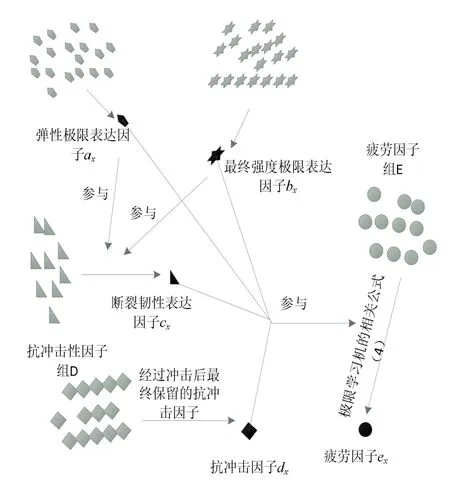
图2 5 种表达因子的具体关系图

因为新型建筑材料的疲劳度与它的弹性极限、强度极限性、断裂韧性、抗冲击性都有着直接的关系，因此在计算得到最佳的疲劳表达因子时，需要将上述4 类最佳表达因子都代入计算，从而得到最终的疲劳因子ex[14]。上述5 种表达因子的具体关系图如图2 所示。

在对提取的弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性因子、疲劳因子进行充分分析得到各自的表达因子后，通过本文预测算法创造的双隐层的前馈神经网络对这些表达因子进行预测，进而达到对复合类新型建筑材料与高度成型类新型建筑材料分别进行充分预测的目的[15]。

3 实验与研究

为准确评估本文提出方法的效果，设置了相应的实验环境下进行效果检测，将本文方法与传统方法进行实验对比。

针对于新型建筑材料力学性能预测的复杂性，需要对实验环境进行数据筛选，本文为完善实验操作并准确地比较本文研究方法与传统方法的差异性，按照步骤划分实验研究操作，如下：

（1）在实验环境内安置多种两大类型的新型建筑材料即复合类新型建筑材料与高度成型类建筑材料，增强预测效果的普遍性以及说服力，针对新型建筑材料中复合类的建筑材料，利用双隐层的前馈神经网络根据弹性极限因子、强度极限因子、断裂韧性因子、抗冲击性表达因子构建具体的虚拟预测概念图如图3 所示。

从该预测概念图中可以看出复合类新型建筑材料的弹性极限、断裂韧性较差，趋于传统建筑材料的恒定值，而强度极限、抗冲击性以及疲劳度有着显著的提升，其数值远远高于传统建筑材料的恒定值且在一定的精确范围内。

（2）针对新型建筑材料中高度成型类的建筑材料，本文依然通过双隐层的前馈神经网络根据5 种表达因子构建了具体的虚拟预测概念图如图4 所示。

从该预测概念图中可以看出高度成型类新型建筑材料的弹性极限与断裂韧性较于传统的建筑材料的恒定值有着显著提升，并且趋于一定的精确范围内，而强度极限与抗冲击性较低于恒定值，而疲劳度却与恒定值基本相同。由此构建双隐层的前馈神经网络结构图进行深度研究（图5）。

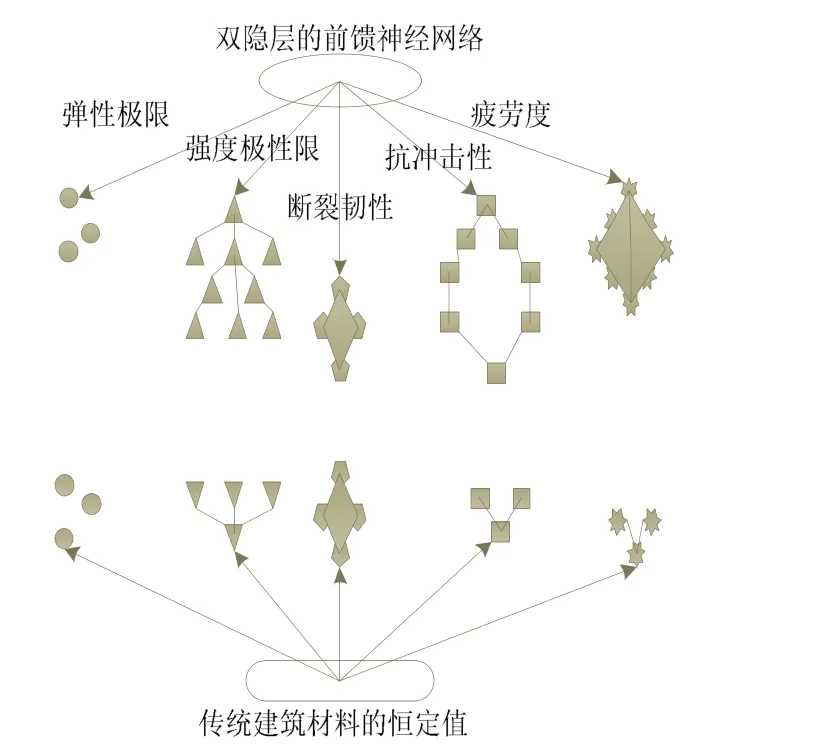
图3 复合类新型建筑材料的预测概念图

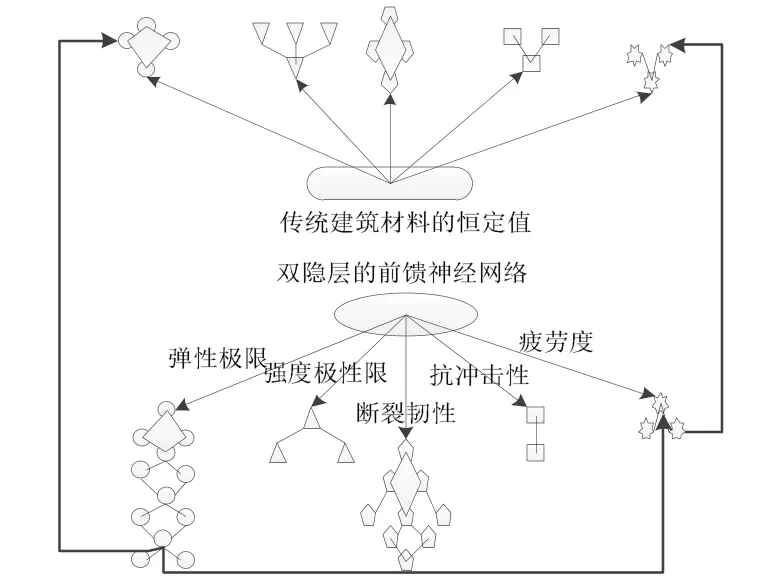
图4 高度成型类新型建筑材料的预测概念图

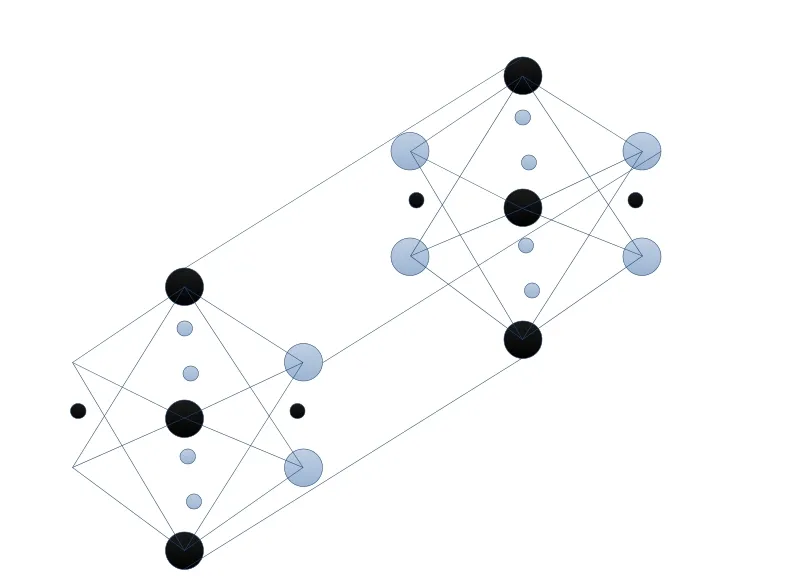
图5 双隐层的前馈神经网络的结构图

该网络结构可以根据新型建筑材料的不同种类自觉地提取相关的力学性能因子，如针对复合类材料如高强、高性能混凝土材料，新型墙体材料这类复合类建筑材料，为了增强预测结果的比较性，在应用时，根据新型建筑材料的类别不同，设置不同的传统方法，分别为复合类新型建筑材料力学性能预测方法与高度成型类新型建筑材料力学性能预测方法（即文献[5],[6]方法）。

（3）在完成上述操作后，提取新型建筑材料力学性能因子参数，并构建提取图示（图6）。

由此获取所需的参数数据，进行实验预测，在预测的过程中要实时记录各自方法的预测效率以及预测时间，合理应用各类方法优势，最终综合评估所有方法的预测结果。

在此实验中，为了进一步提高整体的对比效果，可设置相应的实验参数如表1 所示。

根据上述实验参数可以得到本文方法与文献[5]方法以及文献[6]方法对新型建筑材料力学性能预测的预计整体成本投入对比以及预测效率对比，分别如图7,8 所示，其中的预计整体成本包括材料原价、材料运杂费、运输损耗费以及检验试验费等部分，投入成本由各部分的成本乘以相关系数得出。

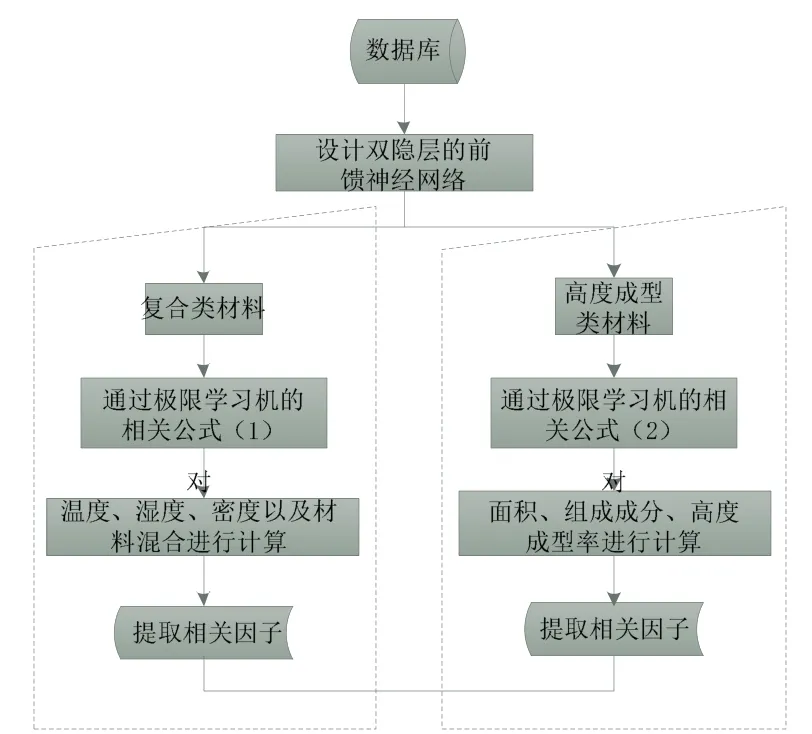
图6 新型建筑材料力学性能因子提取过程

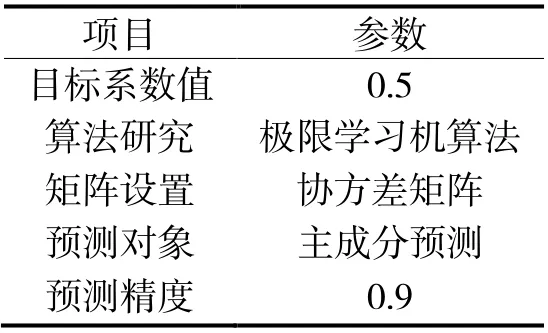
表1 实验参数

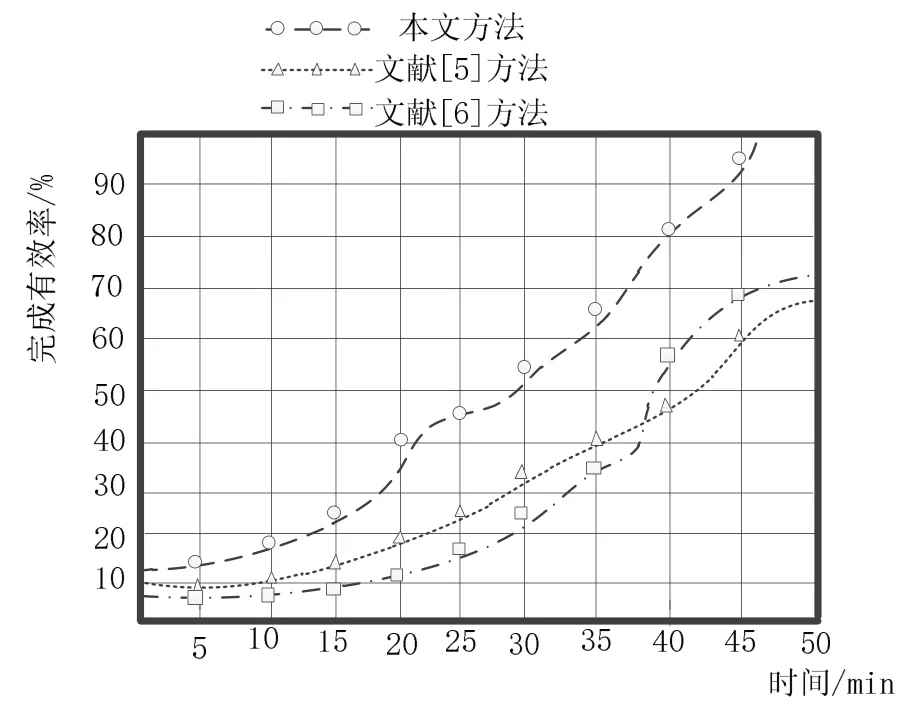
图8 新型建筑材料力学性能预测效率对比图

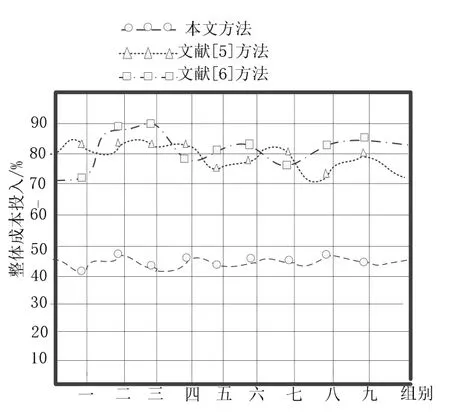
图7 新型建筑材料力学性能预测整体成本投入对比

根据图7,8 可以看出，本文方法比文献[5], [6]方法的预测投入成本都要低很多。在相同的时间内本方法对新型建筑材料的力学性能预测效率也远远快于另外两种方法。造成上述结果是由于本文方法创造的双隐层的前馈神经网络可以完成对新型建筑材料力学性能因子化的处理和整体的因子提取、分析、预测，而因子化的处理大大减少了预测的操作步骤，在提高效率的同时大大减少了资金的投入。

综上所述，本文方法能够更好地预测新型建筑材料的力学性能，具有合理的操作技能，大幅度地降低了成本投入并提高了预测效率。

4 结束语

本文在传统的新型建筑材料的力学性能预测方法的基础上提出了因子化这一理念，实验研究表明，该方法的预测效果明显优于传统的预测方法。本文所提出的这一理念是从极限学习机的算法理念中得到了启发并且整体的预测也以极限学习机作为基础，为该预测领域开辟了新的途径，具有广阔的发展空间，希望能够为接下来该领域的发展提供一定帮助和支持。